Beruflich Dokumente
Kultur Dokumente
Pathria Solution1
Hochgeladen von
Mario Mede RiteOriginalbeschreibung:
Originaltitel
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Pathria Solution1
Hochgeladen von
Mario Mede RiteCopyright:
Verfügbare Formate
Problem 16 We showed that the entropy of a system could be written in the form S = kB H where H is the Eta function of Boltzmann
given by
H=
i
Pi ln Pi
and Pi is the probability of occupation of quantum state i. The purpose of this problem is to explore some properties of this function. (a) For a system having a nite number of states M, show that this function achieves its maximum value when all of these probabilities are equal. Determine from your result the maximum value of the entropy for such a system. Hint: Use a Lagrange multiplier to handle the constraint among the Pi . (b) Now introduce the explicit form Pi = exp(Ei )/Z ( ) given by the canonical ensemble for a system at temperature T = 1/(kB ) and xed volume V. Show by straightforward dierentiation that
S T
=
V
kB T
Pj (j U )2 (kB T )2
where U is the internal energy at temperature T. (c) From the result of part (b), what can you deduce about the behavior of S with increasing temperature and the sign of the heat capacity CV of the system? For a system having a nite number of states M, what would be the slope of a graph of ln CV versus ln T at extremely high temperatures? Problem 17 The Helmholtz free energy of an an ultrarelativistic ideal gas having N particles is
V BT F = N kT [ln(8 N ) + 3 ln( khc ) + 1]
where c is the speed of light. (a) What is the canonical partition function Z ( ) for this gas? Hint: Use Stirlings approximation in reverse to relate the terms in N to N!. (b) Determine the density of states D(E) for this gas by inverting the Laplace transform of the partition function Z ( ). You will need to calculate the contour integral
g (E ) =
1 2i
eE Z ( )d,
Br
where the Bromwich contour Br starts at i, ends at i and lies to the right of all singularities of Z ( ). (c) According to the microcanonical ensemble, we showed in problem 9 that for such a gas has the functional form N )V N E 3N . = ( 1
N ). Use the result of part (b) to determine the unknown function ( Problem 18 This is a revised version of Pathria Problem 3.26. The objective of this problem is to compare the partition function of N identical but distinguishable s-dimensional harmonic oscillators and their thermodynamic properties with Ns identical but distinguishable one-dimensional harmonic oscillators. In addition, the chemical potentials should be compared to deduce that s = s1 . (a) First, assume that each dimension is governed by an independent quantum number ni = 0, 1, 2 so that the energy states of a single s-dimensional oscillator are given by
(n1 ns ) =
i=1
(ni + 1/2) h
Solve the problem by calculating the partition function for each direction and using the factorization theorem to deduce the partition function of the whole system. (b)Show that the energy levels of the system can be written in the form j = (j + s/2) h where j = 0, 1, 2 and that these energy levels have degeneracy (j + s - 1)!/[(j - 1)!s!]. Now obtain the total partition function for the whole system by doing the partition sum of exp(j ) over j, including the degeneracy factor. Hint: Since you already know the answer, evaluate the sum by showing that both expressions have the same power series. (c) Calculate the chemical potentials s and 1 and compare your results. Problem 19 This is a version of Pathria Problem 3.24 page 86. The Hamiltonian of a relativistic particle of rest mass m can be expressed in terms of its canonical momentum p by
H = mc2 (1 +
p2 1/2 ) mc2 m2 c2
2 2 where c is the speed of light and p2 = p2 x + py + pz . Here, energy is measured relative to the rest energy, 2 2 mc , so H becomes p /(2m) in the non-relativistic limit and therefore plays the role of the kinetic energy. The momentum is related to the velocity v by
p=
mv . (1 v 2 /c2 )1/2
(a) Show that these relations are consistent with Hamiltons equations, namely that
H =x p where a is a cartesian component and the dot denotes a time derivative. (b) Use the results for classical averaging in the canonical ensemble (Sekerka 18.5) to show that equipartition takes the form 2
1 m 2
v2 (1 v 2 /c2 )1/2
3 kB T. 2
(c) Use the corresponding expression in terms of p2 to evaluate approximately the thermal average < H > of the kinetic energy in the non relativistic and the extreme relativistic limits and compute the ratio of you results. Problem 20 This problem is adapted from Pathria 3.36 page 88, for which the given answer is wrong because of a typographical error. The potential energy of two dipoles having dipole moments and separated by a vector R of magnitude R can be written in the form
U=
1 )( R )] [ 3( R R3
= R/R. Pathrias expression for U is obtained by choosing R to be along the z-axis where the unit vector R of a spherical coordinate system, in which case R = k and = sin cos i + sin sin j + cos k and similarly for . This gives
U =
[2 cos cos sin sin cos( )] =: 3 G(, , , ). R3 R
The kinetic energy of each dipole can be approximated as if each were a diatomic molecule. In a reference frame where each molecule is rotating but not translating, the kinetic energy takes the form
K (p , p , , p , p , ) :=
1 2 1 2 2 2 (p + p2 (p + p2 / sin ) + / sin ) 2I 2I
where I and I are moments of inertia and p , p , p , p are conjugate momenta to the coordinates , , , . The Hamiltonian is therefore
H (p , p , , , p , p , , ) = K
G. R3
(a) Returning to the general expression for U, show that the instantaneous force exerted on a dipole at R by a dipole located at the origin is given by
F =
1 )( R )]R + 3 ( R ) + 3 ( R ) [3 15( R 4 4 R R R4
(b)The average force is given by 3
F =
exp(H )Fddd d dp dp dp dp . exp(H )ddd d dp dp dp dp
Show that integration over the canonical momenta leads to factors in both integrals that are essential to integration over the coordinates. Cancel any common factors and rewrite the resulting expression for F in terms of integrals over the four angles. give components of force that are not (c) Note that the last two terms in the general expression for F necessarily along R. Show that the average values of these terms give rise to forces that are only along . Hint: G depends only on and only through the variable = . =k R (d) Now expand the exponentials in powers of a 1 and do the remaining integrals only to the extent necessary to obtain a non-vanishing answer to lowest order in a. (e) Compare your result with that of Pathria and give two reasons why his result cannot possibly be correct.
Das könnte Ihnen auch gefallen
- PC235W13 Assignment5 SolutionsDokument10 SeitenPC235W13 Assignment5 SolutionskwokNoch keine Bewertungen
- Wangsness 1 PDFDokument13 SeitenWangsness 1 PDFIhsan FadilahNoch keine Bewertungen
- Selected Solutions - David A.B. Miller Quantum MechanicsDokument53 SeitenSelected Solutions - David A.B. Miller Quantum MechanicsRamzan8850100% (1)
- HW 3 CMDokument9 SeitenHW 3 CMeddiejam1642Noch keine Bewertungen
- Unknown - Szabo, Solutions of Modern Quantum ChemistryDokument312 SeitenUnknown - Szabo, Solutions of Modern Quantum ChemistryVinicius PiccoliNoch keine Bewertungen
- Ward IdentityDokument13 SeitenWard IdentityMritunjay KumarNoch keine Bewertungen
- HW 9 SolutionDokument5 SeitenHW 9 SolutionJuan DavidNoch keine Bewertungen
- Em 6.20Dokument3 SeitenEm 6.20sauciataNoch keine Bewertungen
- PC235W13 Assignment8 SolutionsDokument11 SeitenPC235W13 Assignment8 SolutionskwokNoch keine Bewertungen
- Sakurai Solutions 5-1 5-2Dokument8 SeitenSakurai Solutions 5-1 5-2Raza Ali RazaNoch keine Bewertungen
- Jackson 5 20 Homework SolutionDokument44 SeitenJackson 5 20 Homework SolutionMorodirNoch keine Bewertungen
- Electrics. Pulsars Are Stars That Emit Short BurDokument2 SeitenElectrics. Pulsars Are Stars That Emit Short BurphysicspersonNoch keine Bewertungen
- Spacetime and Geometry: An Introduction To General RelativityDokument525 SeitenSpacetime and Geometry: An Introduction To General RelativitySamuel Johnson Ho100% (2)
- Quantum Mechanics II - Homework 2Dokument6 SeitenQuantum Mechanics II - Homework 2Ale GomezNoch keine Bewertungen
- Quantum Mechanics II - Homework Assignment 7: Alejandro G Omez Espinosa April 7, 2013Dokument5 SeitenQuantum Mechanics II - Homework Assignment 7: Alejandro G Omez Espinosa April 7, 2013Ale GomezNoch keine Bewertungen
- Solucionario PollackDokument7 SeitenSolucionario PollackAaron Chacaliaza RicaldiNoch keine Bewertungen
- Homework Solutions Quantum 3Dokument11 SeitenHomework Solutions Quantum 3fizarimaeNoch keine Bewertungen
- Quantum Mechanics II - Homework Assignment 5: Alejandro G Omez Espinosa March 23, 2013Dokument5 SeitenQuantum Mechanics II - Homework Assignment 5: Alejandro G Omez Espinosa March 23, 2013Ale GomezNoch keine Bewertungen
- Homework 9Dokument7 SeitenHomework 9Ale GomezNoch keine Bewertungen
- Goldstein 22 15 21 23Dokument9 SeitenGoldstein 22 15 21 23Laura SáezNoch keine Bewertungen
- Emii17sol 2 PDFDokument24 SeitenEmii17sol 2 PDFJesus Antonio Jimenez AriasNoch keine Bewertungen
- MSAE3111, Thermodynamics and Statistical MechanicsDokument42 SeitenMSAE3111, Thermodynamics and Statistical MechanicsnacimugNoch keine Bewertungen
- Gold 9Dokument11 SeitenGold 9Feris KamlasiNoch keine Bewertungen
- Quantum Mechanics II - Homework Assignment 8: Alejandro G Omez Espinosa April 15, 2013Dokument4 SeitenQuantum Mechanics II - Homework Assignment 8: Alejandro G Omez Espinosa April 15, 2013Ale GomezNoch keine Bewertungen
- Quantum Mechanics II - Homework 6Dokument6 SeitenQuantum Mechanics II - Homework 6Ale GomezNoch keine Bewertungen
- Goldstein 10.13 - 10.27Dokument6 SeitenGoldstein 10.13 - 10.27Sergio BatistaNoch keine Bewertungen
- Statistical Mechanics SolutionsDokument17 SeitenStatistical Mechanics SolutionsZahra KhanNoch keine Bewertungen
- Lecture 6 Notes, Electromagnetic Theory I: 1. Associated Legendre PolynomialsDokument14 SeitenLecture 6 Notes, Electromagnetic Theory I: 1. Associated Legendre PolynomialsMuzamil ShahNoch keine Bewertungen
- Quality Solutions GoldsteinDokument7 SeitenQuality Solutions GoldsteinJohn HolmanNoch keine Bewertungen
- Thermodynamics Worked Examples PDFDokument20 SeitenThermodynamics Worked Examples PDFJoshua Edokpayi100% (1)
- Homework 5Dokument4 SeitenHomework 5Ale Gomez100% (6)
- Perturbation TheoryDokument4 SeitenPerturbation Theoryapi-3759956100% (1)
- Tutorial 06Dokument1 SeiteTutorial 06Supriyo Dutta100% (1)
- Pathria SolutationDokument4 SeitenPathria Solutationkrasavchik_8650% (2)
- Magnetic Refrigeration ReportDokument16 SeitenMagnetic Refrigeration ReportAbhishekUpadhyay100% (1)
- Physics 715 HW 1Dokument13 SeitenPhysics 715 HW 1Antonildo PereiraNoch keine Bewertungen
- Solutions To Problems in Goldstein, Classical Mechanics, Second EditionDokument70 SeitenSolutions To Problems in Goldstein, Classical Mechanics, Second EditionYhunnior RoberthNoch keine Bewertungen
- Quantum Mechanics II - Homework 3Dokument7 SeitenQuantum Mechanics II - Homework 3Ale GomezNoch keine Bewertungen
- Qualification Exam: Quantum Mechanics: Name:, QEID#76977605: October, 2017Dokument110 SeitenQualification Exam: Quantum Mechanics: Name:, QEID#76977605: October, 2017yeshi janexoNoch keine Bewertungen
- CHP 7 ProblemsDokument5 SeitenCHP 7 ProblemsaishaNoch keine Bewertungen
- Quantum Mechanics - Homework Assignment 4: Alejandro G Omez Espinosa October 10, 2012Dokument8 SeitenQuantum Mechanics - Homework Assignment 4: Alejandro G Omez Espinosa October 10, 2012Ale GomezNoch keine Bewertungen
- Rigid RotorDokument15 SeitenRigid Rotormeghna100% (1)
- Jaynes-Cummings ModelDokument6 SeitenJaynes-Cummings ModelFavio90Noch keine Bewertungen
- (Fiolhais, M.C.N. Et Al.) A Variational Proof of Thomson's TheoremDokument3 Seiten(Fiolhais, M.C.N. Et Al.) A Variational Proof of Thomson's Theoremlev76Noch keine Bewertungen
- SemiclassicalDokument27 SeitenSemiclassicalOmegaUserNoch keine Bewertungen
- Introduction To The AdSCFT CorrespondenceDokument64 SeitenIntroduction To The AdSCFT CorrespondencelunarcausticacNoch keine Bewertungen
- Cap 4Dokument3 SeitenCap 4JulioquanticaNoch keine Bewertungen
- Electricity and Magnetism II - Jackson Homework 8Dokument4 SeitenElectricity and Magnetism II - Jackson Homework 8Ale GomezNoch keine Bewertungen
- EM Problem Set PDFDokument78 SeitenEM Problem Set PDFNadiaNoch keine Bewertungen
- MPDFDokument6 SeitenMPDFDewi Fatmawati0% (1)
- Quantum Field Theory Solution To Exercise Sheet No. 9: Exercise 9.1: One Loop Renormalization of QED A)Dokument20 SeitenQuantum Field Theory Solution To Exercise Sheet No. 9: Exercise 9.1: One Loop Renormalization of QED A)julian fischerNoch keine Bewertungen
- Aerodynamics ExercicesDokument5 SeitenAerodynamics ExercicesMarcRosetNoch keine Bewertungen
- Landmark Experiments in Twentieth-Century PhysicsVon EverandLandmark Experiments in Twentieth-Century PhysicsBewertung: 3 von 5 Sternen3/5 (1)
- Nanomagnetism and SpintronicsVon EverandNanomagnetism and SpintronicsTeruya ShinjoNoch keine Bewertungen
- Fundamental Principles of Modern Theoretical Physics: International Series of Monographs in Natural PhilosophyVon EverandFundamental Principles of Modern Theoretical Physics: International Series of Monographs in Natural PhilosophyNoch keine Bewertungen
- Lectures on Theoretical Physics: Thermodynamics and Statistical MechanicsVon EverandLectures on Theoretical Physics: Thermodynamics and Statistical MechanicsBewertung: 1 von 5 Sternen1/5 (1)
- Dynamical Systems Method for Solving Nonlinear Operator EquationsVon EverandDynamical Systems Method for Solving Nonlinear Operator EquationsBewertung: 5 von 5 Sternen5/5 (1)
- About The Origins of The General Theory of Relativity - Einstein's Search For The TruthDokument7 SeitenAbout The Origins of The General Theory of Relativity - Einstein's Search For The TruthMario Mede RiteNoch keine Bewertungen
- Efecto StarkDokument15 SeitenEfecto StarkMario Mede RiteNoch keine Bewertungen
- Simple Derivation of Metrics!!!Dokument14 SeitenSimple Derivation of Metrics!!!Mario Mede RiteNoch keine Bewertungen
- Sakurai Solutions 1-1 1-4 1-8Dokument4 SeitenSakurai Solutions 1-1 1-4 1-8Mario Mede RiteNoch keine Bewertungen
- Apexi Powerfc Instruction ManualDokument15 SeitenApexi Powerfc Instruction ManualEminence Imports0% (2)
- Drive LinesDokument30 SeitenDrive LinesRITESH ROHILLANoch keine Bewertungen
- rp10 PDFDokument77 Seitenrp10 PDFRobson DiasNoch keine Bewertungen
- Standard Answers For The MSC ProgrammeDokument17 SeitenStandard Answers For The MSC ProgrammeTiwiNoch keine Bewertungen
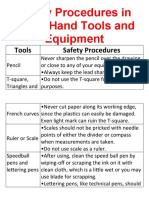
- Safety Procedures in Using Hand Tools and EquipmentDokument12 SeitenSafety Procedures in Using Hand Tools and EquipmentJan IcejimenezNoch keine Bewertungen
- Food ResourcesDokument20 SeitenFood ResourceshiranNoch keine Bewertungen
- ISO 27001 Introduction Course (05 IT01)Dokument56 SeitenISO 27001 Introduction Course (05 IT01)Sheik MohaideenNoch keine Bewertungen
- Caspar Hirschi - The Origins of Nationalism - An Alternative History From Ancient Rome To Early Modern Germany-Cambridge University Press (2012)Dokument255 SeitenCaspar Hirschi - The Origins of Nationalism - An Alternative History From Ancient Rome To Early Modern Germany-Cambridge University Press (2012)Roc SolàNoch keine Bewertungen
- Dwnload Full Principles of Economics 7th Edition Frank Solutions Manual PDFDokument35 SeitenDwnload Full Principles of Economics 7th Edition Frank Solutions Manual PDFmirthafoucault100% (8)
- Man and Historical ActionDokument4 SeitenMan and Historical Actionmama.sb415Noch keine Bewertungen
- The RBG Blueprint For Black Power Study Cell GuidebookDokument8 SeitenThe RBG Blueprint For Black Power Study Cell GuidebookAra SparkmanNoch keine Bewertungen
- Fertilization Guide For CoconutsDokument2 SeitenFertilization Guide For CoconutsTrade goalNoch keine Bewertungen
- Pidsdps 2106Dokument174 SeitenPidsdps 2106Steven Claude TanangunanNoch keine Bewertungen
- KsDokument5 SeitenKsnurlatifahNoch keine Bewertungen
- Kiritsis SolutionsDokument200 SeitenKiritsis SolutionsSagnik MisraNoch keine Bewertungen
- Cisco UCS Adapter TroubleshootingDokument90 SeitenCisco UCS Adapter TroubleshootingShahulNoch keine Bewertungen
- Cloud Comp PPT 1Dokument12 SeitenCloud Comp PPT 1Kanishk MehtaNoch keine Bewertungen
- The cardioprotective effect of astaxanthin against isoprenaline-induced myocardial injury in rats: involvement of TLR4/NF-κB signaling pathwayDokument7 SeitenThe cardioprotective effect of astaxanthin against isoprenaline-induced myocardial injury in rats: involvement of TLR4/NF-κB signaling pathwayMennatallah AliNoch keine Bewertungen
- PDFDokument10 SeitenPDFerbariumNoch keine Bewertungen
- ASHRAE Journal - Absorption RefrigerationDokument11 SeitenASHRAE Journal - Absorption Refrigerationhonisme0% (1)
- postedcontentadminuploadsFAQs20for20Organization PDFDokument10 SeitenpostedcontentadminuploadsFAQs20for20Organization PDFMohd Adil AliNoch keine Bewertungen
- Interlocking Block TechnologyDokument15 SeitenInterlocking Block TechnologyChaula Trivedi100% (5)
- CL57T V4.0Dokument14 SeitenCL57T V4.0dimitriNoch keine Bewertungen
- Sveba Dahlen - SRP240Dokument16 SeitenSveba Dahlen - SRP240Paola MendozaNoch keine Bewertungen
- Drug Addiction Final (Term Paper)Dokument15 SeitenDrug Addiction Final (Term Paper)Dessa Patiga IINoch keine Bewertungen
- Fundamentals of Public Health ManagementDokument3 SeitenFundamentals of Public Health ManagementHPMA globalNoch keine Bewertungen
- Sources of Hindu LawDokument9 SeitenSources of Hindu LawKrishnaKousikiNoch keine Bewertungen
- QuexBook TutorialDokument14 SeitenQuexBook TutorialJeffrey FarillasNoch keine Bewertungen
- 01 托福基础课程Dokument57 Seiten01 托福基础课程ZhaoNoch keine Bewertungen
- Ra 9272Dokument6 SeitenRa 9272janesamariamNoch keine Bewertungen