Beruflich Dokumente
Kultur Dokumente
Resonance Kinematics
Hochgeladen von
rahuljain1Originalbeschreibung:
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Resonance Kinematics
Hochgeladen von
rahuljain1Copyright:
Verfügbare Formate
RESONANCE
Page # 1 Page # 1 Page # 1 Page # 1 Page # 1
TM
MECHANICS MECHANICS MECHANICS MECHANICS MECHANICS
Mechanics is the branch of physics which deals with the cause and
effects of motion of a particle, rigid objects and deformable bodies
etc. Mechanics is classified under two streams namely Kinematics
and Dynamics.
Mechanics
Kinematics Dynamics (or Kinetics)
The word kinematics means It is branch of mechanics which is
science of motion.branch of concerned about the causes (i.e.
the
mechanics which deals with force , torque) that cause motion
study of motion without going of bodies.
into the cause of motion, i.e.
force, torque etc.
1. 1. 1. 1. 1. MOTION AND REST MOTION AND REST MOTION AND REST MOTION AND REST MOTION AND REST
Motion is a combined property of the object and the observer. There
is no meaning of rest or motion without the observer. Nothing is in
absolute rest or in absolute motion.
An object is said to be in motion with respect to a observer, if its
position changes with respect to that observer. It may happen by
both ways either observer moves or object moves.
2. 2. 2. 2. 2. RECTILINEAR MOTION RECTILINEAR MOTION RECTILINEAR MOTION RECTILINEAR MOTION RECTILINEAR MOTION
Rectilinear motion is motion, along a straight line or in one dimension.
It deals with the kinematics of a particle in one dimension.
2. 1 2. 1 2. 1 2. 1 2. 1 Position Position Position Position Position
The position of a particle refers to its location in the space at a certain
moment of time. It is concerned with the question where is the
particle at a particular moment of time ?
2. 2 2. 2 2. 2 2. 2 2. 2 Displacement Displacement Displacement Displacement Displacement
The change in the position of a moving object is known as displacement.
It is the vector joining the initial position of the particle to its final
position during an interval of time.
2. 3 2. 3 2. 3 2. 3 2. 3 Distance Distance Distance Distance Distance
The length of the actual path travelled by a particle during a given time
interval is called as distance. The distance travelled is a scalar quantity
which is quite different from displacement. In general, the distance
travelled between two points may not be equal to the magnitude of the
displacement between the same points.
E pur, si muove.
(Translated: Even so, it does
move.)
When Galileo was declared
a heretic by the Catholic
Church and chose to
recant his beliefs in order
to spare his life, he is known
to have said:
I must altogether
abandon the false opinion
that the Sun is the center
of the world and
immovable, and that the
Earth is not the center of
the world, and moves, and
that I must not hold,
defend, or teach... the said
doctrine.
But afterwards, as he rose
from his kneeling position,
his body weary from
seventy years of age,
legend has it that he
murmured, in Italian the
above statement.
RECTILINEAR MOTION RECTILINEAR MOTION RECTILINEAR MOTION RECTILINEAR MOTION RECTILINEAR MOTION
RESONANCE
Page # 2 Page # 2 Page # 2 Page # 2 Page # 2
TM
Example 1. Ram takes path 1 (straight line) to go from P to Q and Shyam takes path 2 (semicircle).
(a) Find the distance travelled by Ram and Shyam?
P Q
1
2
100 m
(b) Find the displacement of Ram and Shyam?
Sol. (a) Distance travelled by Ram = 100 m
Distance travelled by Shyam = (50 m) = 50 m
(b) Displacement of Ram = 100 m
Displacement of Shyam = 100 m
2. 4 2. 4 2. 4 2. 4 2. 4 Average Velocity Average Velocity Average Velocity Average Velocity Average Velocity (in an interval) :
The average velocity of a moving particle over a certain time interval is defined as the displacement divided by
the lapsed time.
Average Velocity =
erval int time
nt displaceme
for straight line motion, along xaxis, we have
v
av
= v = <v> =
t
x
=
i f
i f
t t
x x
The average velocity is a vector in the direction of displacement. For motion in a straight line, directional
aspect of a vector can be taken care of by +ve and -ve sign of the quantity.
2. 5 2. 5 2. 5 2. 5 2. 5 Average Speed Average Speed Average Speed Average Speed Average Speed (in an interval) (in an interval) (in an interval) (in an interval) (in an interval)
Average speed is defined as the total path length travelled divided by the total time interval during which the
motion has taken place. It helps in describing the motion along the actual path.
Average Speed =
interval time
travelled distance
NOTE :
(a) Average speed is always positive in contrast to average velocity which being a vector, can be positive
or negative.
(b) If the motion of a particle is along a straight line and in same direction then,
average velocity = average speed.
(c) Average speed is, in general, greater than the magnitude of average velocity.
The dimension of velocity and speed is [LT
-1
] and their SI unit is meters per second (m/s)
Example 2. In the example 1, if Ram takes 4 seconds and Shyam takes 5 seconds to go from P to Q, find
(a) Average speed of Ram and Shyam?
(b) Average velocity of Ram and Shyam?
Sol. (a) Average speed of Ram =
4
100
m/s = 25 m/s
Average speed of Shyam =
5
50
m/s = 10 m/s
(b) Average velocity of Ram =
4
100
m/s = 25 m/s
Average velocity of Shyam =
5
100
m/s = 20 m/s
Example 3. A particle travels half of total distance with speed v
1
and next half with speed v
2
along a straight line.
Find out the average speed of the particle?
Sol. Let total distance travelled by the particle be 2s.
Time taken to travel first half =
1
v
s
Time taken to travel next half =
2
v
s
RESONANCE
Page # 3 Page # 3 Page # 3 Page # 3 Page # 3
TM
Average speed =
taken time Total
covered distance Total
=
2 1
v
s
v
s
s 2
+
=
2 1
2 1
v v
v v 2
+
Q.1 A particle covers
4
3
of total distance with speed v
1
and next
4
1
with v
2
. Find the average speed of the
particle?
Ans.
2 1
2 1
3v v
v 4v
+
Q.2. A car is moving with speed 60 Km/h and a bird is moving with speed 90
km/h along the same direction as shown in figure. Find the distance trav-
elled by the bird till the time car reaches the tree?
240 m
Ans. 360 m
2. 6 2. 6 2. 6 2. 6 2. 6 Instantaneous Velocity Instantaneous Velocity Instantaneous Velocity Instantaneous Velocity Instantaneous Velocity (at an instant) :
The velocity at a particular instant of time is known as instantaneous velocity. The term velocity usually
means instantaneous velocity.
V
inst.
=
t
x
lim
0 t
=
dt
dx
In other words, the instantaneous velocity at a given moment (say , t) is the limiting value of the average
velocity as we let t approach zero. The limit as t 0 is written in calculus notation as dx/dt and is called
the derivative of x with respect to t.
2. 7 2. 7 2. 7 2. 7 2. 7 Average acceleration (in an interval): Average acceleration (in an interval): Average acceleration (in an interval): Average acceleration (in an interval): Average acceleration (in an interval):
The average acceleration for a finite time interval is defined as :
Average acceleration =
erval int time
velocity in change
Average acceleration is a vector quantity whose direction is same as that of the change in velocity.
av
a
r
=
t
v
r
=
t
v v
i f
r r
Since for a straight line motion the velocities are along a line, therefore
a
av
=
t
v
=
i f
i f
t t
v v
(where one has to substitute v
f
and v
i
with proper signs in one dimensional motion)
2. 8 2. 8 2. 8 2. 8 2. 8 Instantaneous Acceleration (at an instant): Instantaneous Acceleration (at an instant): Instantaneous Acceleration (at an instant): Instantaneous Acceleration (at an instant): Instantaneous Acceleration (at an instant):
The instantaneous acceleration of a particle is its acceleration at a particular instant of time. It is defined as
the derivative (rate of change) of velocity with respect to time. We usually mean instantaneous acceleration
when we say acceleration. For straight motion we define instantaneous acceleration as :
a =
dt
dv
=
t
v
lim
0 t
and in general
a
r
=
dt
v d
r
=
t
v
lim
0 t
r
The dimension of acceleration is [LT
-2
] and its SI unit is m/s
2
.
RESONANCE
Page # 4 Page # 4 Page # 4 Page # 4 Page # 4
TM
Example 4. Position of a particle as a function of time is given as x = 5t
2
+ 4t + 3. Find the velocity and
acceleration of the particle at t = 2 s?
Sol. Velocity; v =
dt
dx
= 10t + 4
At t = 2 s v = 10(2) + 4 v = 24 m/s
Acceleration; a =
2
2
dt
x d
= 10
Acceleration is constant, so at t = 2 s
a = z10 m/s
2
Q.3 The position of a particle moving on X-axis is given by
x = At
3
+ Bt
2
+ Ct + D.
The numerical values of A, B, C, D are 1, 4, -2 and 5 respectively and SI units are used. Find (a) the
dimensions of A, B, C and D, (b) the velocity of the particle at t = 4 s, (c) the acceleration of the particle at
t = 4s, (d) the average velocity during the interval t =0 to t = 4s, (e) the average acceleration during the interval
t = 0 to t = 4 s.
Ans. [(a) [A] = [LT
-3
], [B] = [LT
-2
], [C] = [LT
-1
] and [D] = [L] ; (b) 78 m/s ; (c) 32 m/s
2
; (d) 30 m/s ; (e) 20 m/s
2
]
3. 3. 3. 3. 3. MO MO MO MO MOTION WITH UNIF TION WITH UNIF TION WITH UNIF TION WITH UNIF TION WITH UNIFORM VEL ORM VEL ORM VEL ORM VEL ORM VELOCIT OCIT OCIT OCIT OCITY YY YY
Consider a particle moving along xaxis with uniform velocity u starting from the point x = x
i
at t = 0.
Equations of x, v, a are : x (t) = x
i
+ ut ; v (t) = u ; a (t) = 0
x t graph is a straight line of slope u through x
i
.
as velocity is constant, v t graph is a horizontal line.
at graph coincides with time axis because a = 0 at all time instants.
x
O
x
i
t
u is negative
s
lo
p
e
=
u
v
O
u
t
positive velocity
v
O
u
t
negative velocity
4. 4. 4. 4. 4. UNIF UNIF UNIF UNIF UNIFORML ORML ORML ORML ORMLY ACCELERA Y ACCELERA Y ACCELERA Y ACCELERA Y ACCELERATED MO TED MO TED MO TED MO TED MOTION TION TION TION TION
If a particle is accelerated with constant acceleration in an interval of time, then the motion is termed as
uniformly accelerated motion in that interval of time.
For uniformly accelerated motion along a straight line (xaxis) during a time interval of t seconds, the
following important results can be used.
(a) v = u + at
(b) s = ut + 1/2 at
2
s = vt 1/2 at
2
x
f
= x
i
+ ut + 1/2 at
2
(c) v
2
= u
2
+ 2as
(d) s = 1/2 (u + v) t
(e) s
n
= u + a/2 (2n 1)
u = initial velocity (at the beginning of interval)
a = acceleration
v = final velocity (at the end of interval)
s = displacement (x
f
x
i
)
x
f
= final coordinate (position)
x
i
= initial coordinate (position)
s
n
= displacement during the n
th
sec
RESONANCE
Page # 5 Page # 5 Page # 5 Page # 5 Page # 5
TM
Example 5. A particle moving rectilinearly with constant acceleration is having initial velocity of 10 m/s. After
some time, its velocity becomes 30 m/s. Find out velocity of the particle at the mid point of its
path?
Sol. Let the total distance be 2x.
distance upto midpoint = x
Let the velocity at the mid point be v
and acceleration be a.
From equations of motion
v
2
= 10
2
+ 2ax ____ (1)
30
2
= v
2
+ 2ax ____ (2)
(2) - (1) gives
v
2
- 30
2
= 10
2
- v
2
v
2
= 500 v =
5 10
m/s
Example 6. A police inspector in a jeep is chasing a pickpocket an a straight road. The jeep is going at its
maximum speed v (assumed uniform). The pickpocket rides on the motorcycle of a waiting
friend when the jeep is at a distance d away, and the motorcycle starts with a constant accelera-
tion a. Show that the pick pocket will be caught if
2ad v
.
Sol. Suppose the pickpocket is caught at a time t after motorcycle starts. The distance travelled by the motor-
cycle during this interval is
2
at
2
1
s =
____ (1)
During this interval the jeep travels a distance
vt d s = +
____ (2)
By (1) and (2),
vt d at
2
1
2
= +
or,
a
ad 2 v v
t
2
=
The pickpocket will be caught if t is real and positive.
This will be possible if
2ad v
2
or,
2ad v
Q.4 A car deccelerates from a speed of 20 m/s to rest in a distance of 100 m. What was its acceleration,
assumed constant?
Ans. [- 2 m/s
2
]
Q. 5 A 150 m long train accelerates uniformly from rest. If the front of the train passes a railway worker 50 m away
from the station at a speed of 25 m/s, what will be the speed of the back part of the train as it
passes the worker?
Ans. [50 m/s]
5. 5. 5. 5. 5. GRAPHS IN UNIF GRAPHS IN UNIF GRAPHS IN UNIF GRAPHS IN UNIF GRAPHS IN UNIFORML ORML ORML ORML ORMLY ACCELERA Y ACCELERA Y ACCELERA Y ACCELERA Y ACCELERATED MO TED MO TED MO TED MO TED MOTION TION TION TION TION (a 0)
x is a quadratic polynomial in terms of t. Hence x t graph is a parabola.
x
i
x
a > 0
t
0
x
i
x
a < 0
t
0
x-t graph
v is a linear polynomial in terms of t. Hence vt graph is a straight line of slope a.
v
u
a is positive
s
l
o
p
e
=
a
t
0
v
u
a is negative
s
lo
p
e
=
a
t
0
RESONANCE
Page # 6 Page # 6 Page # 6 Page # 6 Page # 6
TM
v-t graph
at graph is a horizontal line because a is constant.
a
a
positive
acceleration
t
0
a
a
negative
acceleration
0
a-t graph
6. 6. 6. 6. 6. REACTION TIME REACTION TIME REACTION TIME REACTION TIME REACTION TIME
When a situation demands our immediate action. It takes some time before we really respond. Reaction
time is the time a person takes to observe, think and act.
7 77 77. .. .. DIRECTIONS OF VECTORS IN STRAIGHT LINE MOTION DIRECTIONS OF VECTORS IN STRAIGHT LINE MOTION DIRECTIONS OF VECTORS IN STRAIGHT LINE MOTION DIRECTIONS OF VECTORS IN STRAIGHT LINE MOTION DIRECTIONS OF VECTORS IN STRAIGHT LINE MOTION
In straight line motion, all the vectors (position, displacement, velocity & acceleration) will have only one
component (along the line of motion) and there will be only two possible directions for each vector.
For example, if a particle is moving in a horizontal line (xaxis), the two directions are right and left.
Any vector directed towards right can be represented by a positive number and towards left can be
represented by a negative number.
For vertical or inclined motion, upward direction can be
taken +ve and downward as ve
line of motion
l
i
n
e
o
f
m
o
t
i
o
n
l
i
n
e
o
f
m
o
t
i
o
n
+
+
+
-
-
-
For objects moving vertically near the surface of the earth, the only force acting on the particle is its
weight (mg) i.e. the gravitational pull of the earth. Hence acceleration for this type of motion will
always be a = g i.e. a = 9.8 m/s
2
(ve sign, because the force and acceleration are directed
downwards, If we select upward direction as positive).
NOTE :
(a) If acceleration is in same direction as velocity, then speed of the particle increases.
(b) If acceleration is in opposite direction to the velocity then speed decreases i.e. the particle slows
down. This situation is known as retardation.
Example 7. Mr. Sharma brake his car with constant acceleration from a velocity of 25 m/s to 15 m/s over a
distance of 200m.
(a) How much time elapses during this interval?
(b) What is the acceleration?
(c) If he has to continue braking with the same constant acceleration, how much longer would it take
for him to stop and how much additional distance would he cover?
Sol. (a) We select positive direction for our coordinate system to be the direction of the velocity and choose
the origin so that x
i
= 0 when the braking begins. Then the initial velocity is u
x
= +25 m/s at t = 0, and
the final velocity and position are v
x
= +15 m/s and x = 200 m at time t.
Since the acceleration is constant, the average velocity in the interval can be found from the average
of the initial and final velocities.
v
av, x
=
2
1
(u
x
+ v
x
) =
2
1
(15 + 25) = 20 m/s.
The average velocity can also be expressed as v
av, x
=
t
x
. With
x
= 200 m and
t
= t 0,
we can solve for t:
t =
x av,
v
x
=
20
200
= 10 s.
RESONANCE
Page # 7 Page # 7 Page # 7 Page # 7 Page # 7
TM
(b) We can now find the acceleration using v
x
= u
x
+ a
x
t
a
x
=
t
u v
x x
=
10
25 5 1
= 1 m/s
2
.
The acceleration is negative, which means that the positive velocity is becoming smaller as brakes
are applied (as expected).
(c) Now with known acceleration, we can find the total time for the car to go from velocity u
x
= 25 m/s to
v
x
= 0. Solving for t, we find
t =
x
x x
a
u v
=
1
25 0
= 25 s.
The total distance covered is
x = x
i
+ u
x
t +
2
1
a
x
t
2
= 0 + (25)(25) +
2
1
(1)(25)
2
= 625 312.5 = 312.5 m.
Additional distance covered = 312.5 200 = 112.5 m.
Example 8. A particle is dropped from a tower. It is found that it travels 45 m in the last second of its journey. Find
out the height of the tower?
Sol. Let the total time of journey be n seconds.
Using;
) 1 n 2 (
2
a
u s
n
+ =
45 = 0 +
2
10
) 1 2 ( n n = 5 sec
Height of tower;
h =
2
1
gt
2
=
2
1
10
5
2
= 125 m
Example 9. A particle is dropped from height 100 m and another particle is projected vertically up with velocity
50 m/s from the ground along the same line. Find out the position where two particle will meet?
Sol. Let the upward direction as positive.
Let the particles meet at a distance y from the ground.
y=0m
y=100m u=0 m/s
u=50 m/s
A
B
For particle A,
y
0
= + 100 m
u = 0 m/s
a = 10 m/s
2
y = 100 + 0(t)
2
1
10
t
2
[y = y
0
+ ut +
2
1
at
2
]
= 100 - 5t
2
---- (1)
For particle B,
y
0
= 0 m u = + 50 m/s a = 10 m/s
2
y = 50(t)
2
1
10
t
2
= 50t 5t
2
---- (2)
According to the problem;
50t 5t
2
= 100 5t
2
t = 2 sec
Putting t = 2 sec in eqn. (1),
y = 100 20
= 80 m
Hence, the particles will meet at a height 80 m above the ground.
RESONANCE
Page # 8 Page # 8 Page # 8 Page # 8 Page # 8
TM
Q. 6 A particle is thrown vertically with velocity 20 m/s . Find (a) the distance travelled by the particle in first 3
seconds, (b) displacement of the particle in 3 seconds.
Ans. [25m, 15m]
Q.7 A stone is dropped from a balloon going up with a uniform velocity of 5 m/s. If the balloon was 50 m high when
the stone was dropped, find its height when the stone hits the ground. Take g = 10 m/s
2
.
Ans. [68.5 m]
NOTE:- As the particle is detached from the balloon it is having the same velocity as that of balloon, but its
acceleration is only due to gravity and is equal to g.
8. 8. 8. 8. 8. GRAPHIC GRAPHIC GRAPHIC GRAPHIC GRAPHICAL INTERPRET AL INTERPRET AL INTERPRET AL INTERPRET AL INTERPRETA AA AATION OF SOME QU TION OF SOME QU TION OF SOME QU TION OF SOME QU TION OF SOME QUANTITIES ANTITIES ANTITIES ANTITIES ANTITIES
8. 1 8. 1 8. 1 8. 1 8. 1 Average Velocity Average Velocity Average Velocity Average Velocity Average Velocity
If a particle passes a point P (x
i
) at time t = t
i
and reaches Q (x
f
) at a later time instant t = t
f
, its average
velocity in the interval PQ is V
av
=
t
x
=
i f
i f
t t
x x
This expression suggests that the average velocity is equal to the slope of
the line (chord) joining the points corresponding to P and Q on the xt graph.
x
Q
P
t
O
x
f
x
i
t
i
t
f
8. 2 8. 2 8. 2 8. 2 8. 2 Instantaneous Velocity Instantaneous Velocity Instantaneous Velocity Instantaneous Velocity Instantaneous Velocity
Consider the motion of the particle between the two points P and Q on the xt graph shown. As the point Q
is brought closer and closer to the point P, the time interval between PQ (t, t, t,......) get progressively
smaller. The average velocity for each time interval is the slope of the appropriate dotted line (PQ, PQ,
PQ......). As the point Q approaches P, the time interval approaches zero, but at the same time the slope
of the dotted line approaches that of the tangent to the curve at the point P. As t 0, V
av
(=x/t) V
inst.
Geometrically, as t 0, chord PQ tangent at P.
Hence the instantaneous velocity at P is the slope of the tangent at P in the x t
graph. When the slope of the x t graph is positive, v is positive (as at the point A
in figure). At C, v is negative because the tangent has negative slope. The
instantaneous velocity at point B (turning point) is zero as the slope is zero.
8. 3 8. 3 8. 3 8. 3 8. 3 Instantaneous Acceleration Instantaneous Acceleration Instantaneous Acceleration Instantaneous Acceleration Instantaneous Acceleration
The derivative of velocity with respect to time is the slope
of the tangent in velocity time (vt) graph.
v
t
a<0
a=0
0
a>0
a=0
a=0
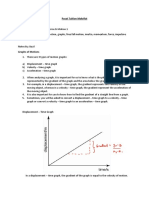
8. 4 8. 4 8. 4 8. 4 8. 4 Displanncement from v - t graph Displanncement from v - t graph Displanncement from v - t graph Displanncement from v - t graph Displanncement from v - t graph
Displacement = x = area under vt graph.
Since a negative velocity causes a negative displacement, areas below the time
axis are taken negative. In similar way, can see that v = a t leads to the conclusion
that area under a t graph gives the change in velocity v during that
interval.
RESONANCE
Page # 9 Page # 9 Page # 9 Page # 9 Page # 9
TM
Example 10. Describe the motion shown by the following velocity-time graphs.
(a) (b)
Sol. (a) During interval AB: velocity is +ve so the particle is moving in +ve direction, but it is slowing down
as acceleration (slope of v-t curve) is negative. During interval BC: particle remains at rest as
velocity is zero. Acceleration is also zero. During interval CD: velocity is -ve so the particle is
moving in -ve direction and is speeding up as acceleration is also negative.
(b) During interval AB: particle is moving in +ve direction with constant velocity and acceleration is
zero. During interval BC: particle is moving in +ve direction as velocity is +ve, but it slows down
until it comes to rest as acceleration is negative. During interval CD: velocity is -ve so the particle
is moving in -ve direction and is speeding up as acceleration is also negative.
Important Points to Remember Important Points to Remember Important Points to Remember Important Points to Remember Important Points to Remember
For uniformly accelerated motion (a 0), xt graph is a parabola (opening upwards if a > 0 and opening
downwards if a < 0). The slope of tangent at any point of the parabola gives the velocity at that instant.
For uniformly accelerated motion (a 0), vt graph is a straight line whose slope gives the acceleration of the
particle.
In general, the slope of tangent in xt graph is velocity and the slope of tangent in vt graph is the acceleration.
The area under at graph gives the change in velocity.
The area between the vt graph gives the distance travelled by the particle, if we take all areas as positive.
Area under vt graph gives displacement, if areas below the taxis are taken negative.
Example 11. For a particle moving along x-axis, velocity-time graph is as shown
in figure. Find the distance travelled and displacement of the particle?
Sol. Distance travelled = Area under v-t graph (taking all areas as +ve.)
Distance travelled = Area of trapezium + Area of triangle
=
( ) 8 6 2
2
1
+
+
5 4
2
1
= 32 + 10 = 42 m
Displacement = Area under v-t graph (taking areas below time axis as -ive.)
Displacement = Area of trapezium Area of triangle
=
( ) 8 6 2
2
1
+
5 4
2
1
= 32 10 = 22 m
Hence, distance travelled = 42 m and displacement = 22 m.
Q.8 For a particle moving along x-axis, following graphs are given. Find the distance travelled by the particle in 10
s in each case?
Ans. [(a) 100m; (b) 50m]
RESONANCE
Page # 10 Page # 10 Page # 10 Page # 10 Page # 10
TM
9. 9. 9. 9. 9. Interpretation of some more Graphs Interpretation of some more Graphs Interpretation of some more Graphs Interpretation of some more Graphs Interpretation of some more Graphs
9. 1 9. 1 9. 1 9. 1 9. 1 Position vs Time graph Position vs Time graph Position vs Time graph Position vs Time graph Position vs Time graph
9.1.1 Zero Velocity
As position of particle is fix at all the time, so the body is at rest.
Slope;
dt
dx
= tan = tan 0 = 0
Velocity of particle is zero
9. 1. 2 9. 1. 2 9. 1. 2 9. 1. 2 9. 1. 2 Uniform Velocity Uniform Velocity Uniform Velocity Uniform Velocity Uniform Velocity
Here tan is constant tan =
dt
dx
dt
dx
is constant.
velocity of particle is constant.
9.1.3 9.1.3 9.1.3 9.1.3 9.1.3 Non uniform velocity Non uniform velocity Non uniform velocity Non uniform velocity Non uniform velocity (increasing with time)
In this case;
As time is increasing, is also increasing.
dt
dx
= tan is also increasing
Hence, velocity of particle is increasing.
9.1.4 9.1.4 9.1.4 9.1.4 9.1.4 Non uniform velocity (decreasing with time) Non uniform velocity (decreasing with time) Non uniform velocity (decreasing with time) Non uniform velocity (decreasing with time) Non uniform velocity (decreasing with time)
In this case;
As time increases, decreases.
dt
dx
= tan also decreases.
Hence, velocity of particle is decreasing.
9. 2 9. 2 9. 2 9. 2 9. 2 Velocity vs time graph Velocity vs time graph Velocity vs time graph Velocity vs time graph Velocity vs time graph
9.2.1 9.2.1 9.2.1 9.2.1 9.2.1 Zero acceleration Zero acceleration Zero acceleration Zero acceleration Zero acceleration
Velocity is constant.
tan = 0
dt
dv
= 0
Hence, acceleration is zero.
9. 2. 2 9. 2. 2 9. 2. 2 9. 2. 2 9. 2. 2 Uniform acceleration Uniform acceleration Uniform acceleration Uniform acceleration Uniform acceleration
tan is constant.
dt
dv
= constant
Hence, it shows constant acceleration.
9. 2. 3 9. 2. 3 9. 2. 3 9. 2. 3 9. 2. 3 Uniform retardation Uniform retardation Uniform retardation Uniform retardation Uniform retardation
Since > 90
tan is constant and negative.
dt
dv
= negative constant
Hence, it shows constant retardation.
RESONANCE
Page # 11 Page # 11 Page # 11 Page # 11 Page # 11
TM
9. 3 9. 3 9. 3 9. 3 9. 3 Acceleration vs time graph Acceleration vs time graph Acceleration vs time graph Acceleration vs time graph Acceleration vs time graph
9.3.1 Constant acceleration 9.3.1 Constant acceleration 9.3.1 Constant acceleration 9.3.1 Constant acceleration 9.3.1 Constant acceleration
tan = 0
dt
da
= 0
Hence, acceleration is constant.
9.3.2 Uniformly increasing acceleration 9.3.2 Uniformly increasing acceleration 9.3.2 Uniformly increasing acceleration 9.3.2 Uniformly increasing acceleration 9.3.2 Uniformly increasing acceleration
is constant.
0 < < 90 tan > 0
dt
da
= tan = constant > 0
Hence, acceleration is uniformly increasing with time.
9.3.3 Uniformly decreasing acceleration 9.3.3 Uniformly decreasing acceleration 9.3.3 Uniformly decreasing acceleration 9.3.3 Uniformly decreasing acceleration 9.3.3 Uniformly decreasing acceleration
Since > 90
tan is constant and negative.
dt
da
= negative constant
Hence, acceleration is uniformly decreasing with time
Example 12. The displacement vs time graph of a particle moving along a straight line is
shown in the figure. Draw velocity vs time and acceleration vs time graph.
Sol: x = 4t
2
v =
dt
dx
= 8t
Hence, velocity-time graph is a straight line having slope i.e. tan = 8.
a =
dt
dv
= 8
Hence, acceleration is constant throughout and is equal to 8.
Problem 10. The displacement vs time graph of a particle moving along a straight line is shown in the figure.
Draw velocity vs time and acceleration vs time graph.
RESONANCE
Page # 12 Page # 12 Page # 12 Page # 12 Page # 12
TM
11. 11. 11. 11. 11. MO MO MO MO MOTION WITH NON-UNIF TION WITH NON-UNIF TION WITH NON-UNIF TION WITH NON-UNIF TION WITH NON-UNIFORM ACCELERA ORM ACCELERA ORM ACCELERA ORM ACCELERA ORM ACCELERATION TION TION TION TION (use of def (use of def (use of def (use of def (use of definit init init init inite int e int e int e int e integrals) egrals) egrals) egrals) egrals)
x =
f
i
t
t
dt ) t ( v (displacement in time interval t = t
i
to t
f
)
The expression on the right hand side is called the definite integral of v(t) between
t = t
i
and t = t
f
. . Similarly change in velocity
v = v
f
v
i
=
f
i
t
t
dt ) t ( a
Table 2 : Some quantities defined as derivatives and integrals.
v(t) =
dt
dx
v = slope of xt graph
a (t) =
dt
dv
a = slope of vt graphs
F (t) =
dt
dp
F = slope of pt graph (p = linear momentum)
x =
dx
=
f
i
t
t
dt ) t ( v
x = area under vt graph
v =
dv
=
f
i
t
t
dt ) t ( a
v = area under at graph
p =
dp
=
f
i
t
t
dt ) t ( F p = area under Ft graph
W =
dW
=
f
i
x
x
dx ) x ( F
W = area under Fx graph
12. 12. 12. 12. 12. SOL SOL SOL SOL SOLVING PR VING PR VING PR VING PR VING PROBLEMS WHICH INV OBLEMS WHICH INV OBLEMS WHICH INV OBLEMS WHICH INV OBLEMS WHICH INVOL OL OL OL OLVES NONUNIF VES NONUNIF VES NONUNIF VES NONUNIF VES NONUNIFORM ACCELERA ORM ACCELERA ORM ACCELERA ORM ACCELERA ORM ACCELERATION TION TION TION TION
12.1 12.1 12.1 12.1 12.1 Acceleration depending on velocity v or time t Acceleration depending on velocity v or time t Acceleration depending on velocity v or time t Acceleration depending on velocity v or time t Acceleration depending on velocity v or time t
By definition of acceleration, we have a =
dt
dv
. If a is in terms of t,
v
v
0
dv
=
t
0
dt ) t ( a
. If a is in
terms of v,
=
t
0
v
v
dt
) v ( a
dv
0
. On integrating, we get a relation between v and t, and then
using
x
x
0
dx
=
t
0
dt ) t ( v , x and t can also be related.
12. 2 12. 2 12. 2 12. 2 12. 2 Acceleration depending on velocity v or position x Acceleration depending on velocity v or position x Acceleration depending on velocity v or position x Acceleration depending on velocity v or position x Acceleration depending on velocity v or position x
a =
dt
dv
a =
dx
dv
dt
dx
a =
dt
dx
dx
dv
a = v
dx
dv
This is another important expression for acceleration.
If a is in terms of x,
v
v
0
dv v
=
x
x
0
dx ) x ( a
.
RESONANCE
Page # 13 Page # 13 Page # 13 Page # 13 Page # 13
TM
If a is in terms of v,
=
x
x
v
v
0 0
dx
) v ( a
dv v
On integrating, we get a relation between x and v. Using
x
x
0
) x ( v
dx
=
t
0
dt
, we can relate x and t.
Example 13. An object starts from rest at t = 0 and accelerates at a rate given by a = 6t. What is
(a) its velocity and
(b) its displacement at any time t?
Sol. As acceleration is given as a function of time,
=
t
t
v(t)
) v(t
0 0
a(t)dt dv
Here t
0
= 0 and v(t
0
) = 0
v(t) =
t
0
6tdt
=
0
t
2
t
6
2
= 6 (
2
t
2
- 0) = 3t
2
So, v(t) = 3t
2
As
=
t
t
0
v(t)dt x
=
t
0
2
dt 3t x
=
0
t
3
t
3
3
0
3
t
3
3
= t
3
Hence, velocity v(t) = 3t
2
and displacement
3
t = x
Q.9. For a particle moving along x-axis, acceleration is given as
2
2v a = . If the speed of the particle is v
0
at
x = 0, find speed as a function of x.
Ans. [
2x
0
e v v = ]
Q. 10. For a particle moving along x-axis, velocity is given as a function of time as v = 2t
2
+ sint. At t = 0, particle is
at origin. Find the position as a function of time?
Ans. [
1 cos(t) t
3
2
x
3
+ =
]
RESONANCE
Page # 14 Page # 14 Page # 14 Page # 14 Page # 14
TM
S U MMA R Y S U MMA R Y S U MMA R Y S U MMA R Y S U MMA R Y
Rectilinear Motion Rectilinear Motion Rectilinear Motion Rectilinear Motion Rectilinear Motion: Rectilinear motion is motion,
along a straight line or in one dimension.
Displacement : Displacement : Displacement : Displacement : Displacement : The vector joining the initial position
of the particle to its final position during an interval of
time.
Distance : Distance : Distance : Distance : Distance : The length of the actual path travelled by
a particle during a given time interval
Average Velocity Average Velocity Average Velocity Average Velocity Average Velocity =
erval int time
nt displaceme
=
i f
i f
t t
x x
Average Speed Average Speed Average Speed Average Speed Average Speed =
interval time
travelled distance
Instantaneous Velocity : Instantaneous Velocity : Instantaneous Velocity : Instantaneous Velocity : Instantaneous Velocity : V
inst.
=
t
x
lim
0 t
=
dt
dx
Average Acceleration Average Acceleration Average Acceleration Average Acceleration Average Acceleration
=
erval int time
velocity in change
=
i f
i f
t t
v v
Instantaneous Acceleration : Instantaneous Acceleration : Instantaneous Acceleration : Instantaneous Acceleration : Instantaneous Acceleration :
a =
dt
dv
=
t
v
lim
0 t
Equations of Motion Equations of Motion Equations of Motion Equations of Motion Equations of Motion
(a) v = u + at
(b) s = ut + 1/2 at
2
s = vt 1/2 at
2
x
f
= x
i
+ ut + 1/2 at
2
(c) v
2
= u
2
+ 2as
(d) s = 1/2 (u + v) t
(e) s
n
= u + a/2 (2n 1)
Important Points to Remember Important Points to Remember Important Points to Remember Important Points to Remember Important Points to Remember
For uniformly accelerated motion (a 0), xt graph is
a parabola (opening upwards if a > 0 and opening
downwards if a < 0). The slope of tangent at any point
of the parabola gives the velocity at that instant.
For uniformly accelerated motion (a 0), vt graph is
a straight line whose slope gives the acceleration of
the particle.
In general, the slope of tangent in xt graph is velocity
and the slope of tangent in vt graph is the
acceleration.
The area under at graph gives the change in velocity.
The area between the vt graph gives the distance
travelled by the particle, if we take all areas as
positive.
Area under vt graph gives displacement, if areas
below the taxis are taken negative.
Maxima and Minima Maxima and Minima Maxima and Minima Maxima and Minima Maxima and Minima
Conditions for maxima are:
dx
dy
= 0 (b)
2
2
dx
y d
< 0
Conditions for minima are:
dx
dy
= 0(b)
2
2
dx
y d
> 0
Motion with Non-Uniform Acceleration Motion with Non-Uniform Acceleration Motion with Non-Uniform Acceleration Motion with Non-Uniform Acceleration Motion with Non-Uniform Acceleration
x =
f
i
t
t
dt ) t ( v
v = v
f
v
i
=
f
i
t
t
dt ) t ( a
Solving Problems which Involves Nonuniform Solving Problems which Involves Nonuniform Solving Problems which Involves Nonuniform Solving Problems which Involves Nonuniform Solving Problems which Involves Nonuniform
Acceleration Acceleration Acceleration Acceleration Acceleration
If a is in terms of t,
v
v
0
dv
=
t
0
dt ) t ( a
If a is in terms of v,
=
t
0
v
v
dt
) v ( a
dv
0
If a is in terms of x,
v
v
0
dv v
=
x
x
0
dx ) x ( a
.
If a is in terms of v,
=
x
x
v
v
0 0
dx
) v ( a
dv v
RESONANCE
Page # 15 Page # 15 Page # 15 Page # 15 Page # 15
TM
Exercise 1
OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS (RECTILINEAR MOTIN) (RECTILINEAR MOTIN) (RECTILINEAR MOTIN) (RECTILINEAR MOTIN) (RECTILINEAR MOTIN) BA BA BA BA BAT TT TTCH - CC CH - CC CH - CC CH - CC CH - CC
1. A motor car is going due north at a speed of 50 km/h. It makes a 90 left turn without changing the speed. The
change in the velocity of the car is about
(A) 50 km/h towards west (B) 50 2 km/h towards south-west
(C) 50 2 km/h towards north-west (D) zero
2. A particle has a velocity u towards east at t = 0. Its acceleration is towards west and is constant, Let x
A
and x
B
be the
magnitude of displacements in the first 10 seconds and the next 10 seconds.
(A) x
A
< x
B
(B) x
A
= x
B
(C) x
A
> x
B
(D) the information is insufficient to decide the relation of x
A
with x
B
.
3. A ball takes t seconds to fall from a height h
1
and 2t seconds to fall from a height h
2
. Then h
1
/h
2
is
(A) 2 (B) 4 (C) 0.5 (D) 0.25
4. A body starts from rest and is uniformly acclerated for 30 s. The distance travelled in the first 10 s is x
1
, next 10 s is
x
2
and the last 10 s is x
3
. Then x
1
: x
2
: x
3
is the same as
(A) 1 : 2 : 4 (B) 1 : 2 : 5 (C) 1 : 3 : 5 (D) 1 : 3 : 9
5. A stone is released from an elevator going up with an acceleration a. The acceleration of the stone after the release is
(A) a upward (B) (g-a) upward (C) (g-a) downward (D) g downward
6. A person standing near the edge of the top of a building throws two balls A and B. The ball A is thrown vertically
downward and the ball B is thrown vertically upward with the same speed. The ball A hits the ground with a speed
A
and the ball B hits the ground with a speed
B
. We have
(A)
A
>
B
(B)
A
<
B
(C)
A
=
B
(D) the relation between A and B depends on height of the building above the ground.
7. Figure shows position-time graph of two cars A and B.
(A) Car A is faster than car B.
(B) Car B is faster than car A.
(C) Both cars are moving with same velocity.
A
0
5
x(m)
B
(D) Both cars have positive acceleration.
8. The displacementtime graph of a moving particle is shown below. The
instantaneous velocity of the particle is negative at the point :
(A) C (B) D
t
x
C
D
E F
(C) E (D) F
9. A particle starts from rest and moves along a straight line with constant acceleration. The variation of velocity v with
displacement S is :
(A)
S
v
(B)
v
S
C)
v
S
(D)
v
S
10. The displacement time graphs of two particles A and B are straight lines making angles of respectively 30
0
and 60
0
with the time axis. If the velocity of A is v
A
and that of B is v
B
, then the value of
B
A
v
v
is
(A) 1/2 (B) 1/ 3 (C) 3 (D) 1/3
11. The initial velocity of a particle is u (at t=0) and the acceleration f is given by (f = at). Which of the following
relations is valid?
(A) v = u + at
2
(B) v = u +
2
at
2
(C) v = u + at (D) v = u
12. A stone is dropped into a well in which the level of water is h below the top of the well. If v is velocity of sound,
the time T after which the splash is heard is given by
(A) T = 2h/v (B)
v
h
g
h 2
T + =
(C)
v 2
h
g
h 2
T + =
(D)
v
h 2
g 2
h
T + =
RESONANCE
Page # 16 Page # 16 Page # 16 Page # 16 Page # 16
TM
13. A body is released from the top of a tower of height h metre. It takes T seconds to reach the ground. Where
is the ball at the time T/2 seconds ?
(A) at h/4 metre from the ground (B) at h/2 metre from the ground
(C) at 3h/4 metre from the ground (D) depend upon the mass of the ball
14. A stone is thrown vertically upward with an initial velocity u from the top of a tower, reaches the ground with a
velocity 3u. The height of the tower is:
(A)
g
3u
2
(B)
g
4u
2
(C)
g
6u
2
(D)
g
9u
2
15. A particle starts from rest with uniform acceleration a. Its velocity after n seconds is v. The displacement of the
body in the last two seconds is :
(A)
n
1) - 2v(n
(B)
n
1) - v(n
(C)
n
1) v(n +
(D)
n
1) 2v(2n +
16. Consider the motion of the tip of the minute hand of a clock. In one hour
(A) the displacement is zero (B) the distance covered is zero
(C) the average speed is zero (D) the average velocity is zero
17. A particle moves along the X-axis as x = u(t 2) + a(t 2)
2
(A) the initial velocity of the particle is u (B) the acceleration of the particle is a
(C) the acceleration of the particle is 2a (D) at t =2s particle is at the origin.
18. Mark the correct statements for a particle going on a straight line:
(A) If the velocity and acceleration have opposite sign, the object is slowing down.
(B) If the position and velocity have opposite sign, the particle is moving towards the origin.
(C) If the velocity is zero at an instant, the acceleration should also be zero at that instant.
(D) If the velocity is zero for a time interval, the acceleration is zero at any instant within the time interval.
19. The velocity of a particle is zero at t = 0
(A) The acceleration at t = 0 must be zero
(B) The acceleration at t = 0 may be zero.
(C) If the acceleration is zero from t = 0 to t = 10 s, the speed is also zero in this interval.
(D) If the speed is zero from t = 0 to t = 10 s the acceleration is also in the interval.
20. Mark the correct statements:
(A) The magnitude of the velocity of a particle is equal to its speed.
(B) The magnitude of average velocity in an interval is equal to its average speed in that interval.
(C) It is possible to have a situation in which the speed of a particle is always zero but the average speed is not zero
(D) It is possible to have a situation in which the speed of the particle is never zero but the average speed in an
interval is zero.
21. The velocity-time plot for a particle moving on a straight line is shown in fig.
(A) The particle has constant acceleration
(B) The particle has never turned around.
(C) The particle has zero displacement
(D) The average speed in the interval 0 to 10s is the same as the
10 20 30
t(s)
-10
-20
10
0
v(m/s)
average speed in the interval 10s to 20s.
SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS
1. A particle covers each 1/3 of the total distance with speed v
1
, v
2
and v
3
respectively. Find the average speed of the
particle ?
2. The position of a particle moving on x-axis is given by x = 4t
3
+ 3t
2
+ 6t + 4. Find
(a) The velocity and acceleration of particle at t = 5 s.
(b) The average velocity and average acceleration during the interval t = 0 to t = 5 s, x = 4t
3
+ 3t
2
+ 6t + 4
(a) The velocity and acceleration of particle at t = 5 s.
(b) The average velocity and average acceleration during the interval t = 0 to t = 5 s.
3. A train starts from rest and moves with a constant acceleration of 2.0 m/s
2
for half a minute. The brakes are then
applied and the train comes to rest in one minute. Find (a) the total distance moved by the train, (b) the maximum
speed attained by the train and (c) the position(s) of the train at half the maximum speed.
4. A particle starts from rest with a constant acceleration. At a time t second, the speed is found to be 100 m/s and one
second later the speed becomes 150 m/s. Find (a) the acceleration and (b) the distance travelled during the (t+1)
th
second.
5. For a particle moving along x-axis, following graphs
are given. Find the distance travelled by
the particle in 10 s in each case.
t(s)
x(m)
10
10
(A)
(B)
t(s)
v(m/s)
10 0
10
2
RESONANCE
Page # 17 Page # 17 Page # 17 Page # 17 Page # 17
TM
6. For a particle moving along x-axis, velocity-time graph is as shown in
figure. Find the distance travelled and displacement of the
particle? Also find the average velocity of the particle?
7. The acceleration of a cart started at t = 0, varies with
time as shown in figure . Find the distance travelled
in 30 seconds and draw the position-
time graph.
8. For a particle moving rectilinearly, acceleration as a function of speed is given as a = 8v
2
. Find the speed as a
function of x if the particle is having a speed of v
0
at x = 0?
9. Under what conditions does the magnitude of the average velocity equal to the average speed.
10. Can an object have increasing speed but its acceleration decreases? If yes, give an example; if not, explain why?
11. Figure shows four paths along which obejcts move from a starting point to
a final point (particle is moving along the same straight line), all in the
same time. The paths pass over a grid of equally spaced straight
lines. Rank the paths according to
(a) the average velocity of the objects and
(b) the average speed of the objects, greatest first.
12. A man walking with a speed '
v
' constant in magnitude and direction passes under a lantern hanging at a
height H above the ground. Find the velocity with which the edge of the shadow of the man's head moves over
the ground, if his height is '
h
'.
13. An elevator is descending with uniform acceleration. To measure the acceleration , a person in the elevator drops
a coin at the moment the elavator starts. The coin is 6 ft above the floor of the elevator at time it is dropped. The
person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the
elevator. [Take g = 32 ft/s
2
]
14. When a model rocket is launched, the propellant burns
for a few seconds, accelerating the rocket upward. After
burnout, the rocket moves upward for a while and then
begins to fall. A parachute opens shortly after the rocket
starts down. The parachute slows the rocket to keep it
from breaking when it lands. The figure here shows
velocity data from the flight of the model rocket. Use the
data to answer the following.
(a) How fast was the rocket climbing when the engine
stopped?
(b) For how many seconds did the engine burn?
(c) When did the rocket reach its
highest point? What was its
velocity then?
(d) When did the parachute open up ? How fast was the rocket falling then?
(e) How long did the rocket fall before the parachute opened?
(f) When was the rocket's acceleration greatest?
(g) When was the acceleration constant? What was its value then (to the nearest interger)?
1. A part i cl e of mass 10
2
kg i s movi ng al ong t he posi t i ve xaxi s under t he i nf l uence of a f orce
F(x) =
2
x 2
K
where K = 10
2
N m
2
. At time t = 0 it is at x = 1.0 m and its velocity is v = 0. Find
(i) its velocity when it reaches x = 0.50 m
(ii) the time at which it reaches x = 0.25 m. [ JEE '98, 8 ]
2. In 1.0 sec. a particle goes from point A to point B moving in a semicircle of
radius 1.0 m. The magnitude of average velocity is: [JEE '99, 2]
(A) 3.14 m/sec (B) 2.0 m/sec
(C) 1.0 m/sec (D) zero
RESONANCE
Page # 18 Page # 18 Page # 18 Page # 18 Page # 18
TM
3. A ball is dropped vertically from a height d above the ground. It hits the ground and bounces up vertically to a
height d/2. Neglecting subsequent motion and air resistance, its velocity v varies with the height h above the
ground as [ JEE '2000, 3 ]
(A) (B) (C) (D)
4. A block is moving down a smooth inclined plane starting from rest at time t = 0. Let S
n
be the distance travelled by
the block in the interval t = n 1 to t = n. The ratio
1 n
n
S
S
+
is [JEE Scr. 2004, 3]
(A)
n 2
1 n 2
(B)
1 n 2
1 n 2
+
(C)
1 n 2
1 n 2
+
(D)
1 n 2
n 2
5. A particle is initially at rest, It is subjected to a linear acceleration a , as shown
in the figure. The maximum speed attained by the particle is
[JEE Scr. 2004; 3]
(A) 605 m/s (B) 110 m/s (C) 55 m/s (D) 550 m/s
6. The velocity displacement graph of a particle moving along a straight line is shown.
The most suitable acceleration-displacement graph will be [JEE Scr. 2005; 3]
(A) (B) (C) (D)
EXERCISE # 1 EXERCISE # 1 EXERCISE # 1 EXERCISE # 1 EXERCISE # 1
OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS
1. B 2. D 3. D 4. C
5. D 6. C 7. C 8. C
9. B 10. D 11. B 12. B
13. C 14. B 15. A 16. A,D
17. C,D 18. A,B,D 19. B,C,D 20. A 21.A,D
SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS
1.
3 1 3 2 2 1
3 2 1
v v v v v v
v v 3v
+ +
2. (a) v
t = 5 s
= 336 units, a
t = 5 s
= 126 units ; (b) <v> = 121
units, <a> = 66 units
3. (a) 2.7 km , (b) 60 m/s, (c) 225 m and 2.25 km
4. (a) 50 m/s
2
; (b) 125 m 5. (A) 0; (B) 60m
6. distance travelled = 10 m; displacement = 6 m; average
velocity = 1.2 m/s
7. 1000 ft. ,
straight line
( ) l j y j s[ kk
parabolic curve
( ) i j oy h; o
parabolic curve ( ) i j oy h; o
8. v = v
0
e
8x
9. < v
r
> = <v>
time
t displacmen
=
time
travelled ce tan dis
When the distance travelled is equal to the displacement
of the particle, i.e. particle moves along the straight line
in the same direction without reversing the direction of
motion.
10. Yes. Speed of object will increase if acceleration is in
the direction of velocity, yet its magnitude may
decrease.
a =
dt
dv
= slope of the curve.
acceleration (slope of the curve) is decreasing with time
yet the speed is increasing.
11. (a) > <
1
v
r
= > <
2
v
r
= > <
3
v
r
= > <
4
v
r
(b) v
4, avg
> v
1, avg
= v
2, avg
> v
3, avg
12.
h H
H
v 13. 20 ft/s
2
14. (a) 190 ft/s (b) 2 s (c) 8 s, 0 ft/s
(d) 10.8 s, 90 ft/s (e) 2.8 s
(f) greatest acceleration happens 2 s after launch
(g) constant acceleration between 2 and 10.8 s, 32 ft/s
2
.
EXERCISE # 2 EXERCISE # 2 EXERCISE # 2 EXERCISE # 2 EXERCISE # 2
1. (i)
V
r
=
1
i
m/s (ii) t =
4
3
3
+
2. B 3. A 4. B 5. C 6. B
RESONANCE Page # 19 Page # 19 Page # 19 Page # 19 Page # 19
TM
RELA RELA RELA RELA RELATIVE MO TIVE MO TIVE MO TIVE MO TIVE MOTION TION TION TION TION
Motion is a combined property of the object under study and the
observer. Motion is always relative, there is no such term like absolute
motion or absolute rest. Motion is always defined with respect to an
observer or reference frame.
Reference frame :
Reference frame is an axis system from which motion is observed. A
clock is attached to measure time. Reference frame can be stationary
or moving. There are two types of reference frame:
(i) Inertial reference frame : A frame of reference in which Newtons
first law is valid is called as inertial reference frame.
(ii) Non-inertial reference frame : A frame of reference in which
Newtons first law is not valid is called as non-inertial reference frame.
Note : Earth is by definition a non-inertial reference frame because of its cen-
tripetal acceleration towards sun. But, for small practical applications
earth is assumed stationary hence, it behaves as an inertial reference
frame.
RELA RELA RELA RELA RELATIVE VEL TIVE VEL TIVE VEL TIVE VEL TIVE VELOCIT OCIT OCIT OCIT OCITY YY YY
Definition : Relative velocity of a particle (object) A with respect to B
is defined as the velocity with which A appears to move is B if consid-
ered to be at rest. In other words, it is the velocity with which A appears
to move as seen by the B considering itself to be at rest.
Relative motion along straight line -
v
A
=
dt
dx
A
, v
B
=
dt
dx
B
x
BA
= x
B
x
A
v
BA
=
dt
dx
B
dt
dx
A
v
BA
= v
B
v
A
v
AA
= v
A
v
A
= 0 (velocity of A with respect to A)
Note : velocity of an object w.r.t. itself is always zero.
Impossibility is a
relative concept.
If my Theory of
relativity is proven
successful, Germany
will claim me as a
German and France
will declare that I
am a citizen of the
world. Should my
theory prove untrue,
France will say that
I am a German and
Germany will declare
that I am a Jew.
-Einstein
RELA RELA
RELA RELA RELATIVE MO TIVE MO
TIVE MO TIVE MO TIVE MOTION TION
TION TION TION
RESONANCE Page # 20 Page # 20 Page # 20 Page # 20 Page # 20
TM
Ex.1 An object A is moving with 5 m/s and B is moving with 20 m/s in the same direction. (Positive x-axis)
(i) Find velocity of B with respect to A.
Sol. v
B
= 20 i
m/s v
A
= 5 i
m/s v
B
v
A
= 15 i
m/s
(ii) Find velocity of A with respect to B
Sol. v
B
= 20 i
m/s, v
A
= 15 i
m/s v
AB
= v
A
v
B
= 15 i
m/s
Note : v
BA
= v
AB
Ex.2 Two objects A and B are moving towards each other with velocities 10 m/s and 12 m/s respectively a shown.
(i) Find out velocity of A with respect to B.
Sol. v
AB
= v
A
v
B
= (10) (12) = 22 m/s towards right.
(ii) Find out velocity of B with respect to A
v
BA
= v
B
v
A
= (12) (10) = 22 m/s towards left.
Velocity of Approach
It is the rate at which a separation between two moving particles decreases.
If separation decreases velocity of approach is positive,
Velocity of approach = 22 m/s
Velocity of approach = 15 m/s
If separation increases, velocity of approach is negative. It is mainly called velocity of separation.
Velocity of separation -
It is the rate with which separation between two moving object increases.
Velocity of separation = 2 m/s
Velocity of separation = 15 m/s
Illustration :
Two balls A and B are moving in the same direction with equal velocities, find out their relative velocity.
Velocity of A with respect to B( )
AB
v
r
= 0
RESONANCE Page # 21 Page # 21 Page # 21 Page # 21 Page # 21
TM
Illustration :
A and B are thrown vertically upward with velocity, 5 m/s and 10 m/s respectively (g = 10 m/s
2
. Find separa-
tion between them after one second
Sol. S
A
= ut
2
1
gt
2
= 5t
2
1
10 t
2
= 5 1 5 1
2
= 5 5 = 0
S
B
= ut
2
1
gt
2
. = 10 1
2
1
10 1
2
= 10 5 = 5
S
B
S
A
= separation = 5m.
Alter :
By relative
BA
a
r
=
B
a
r
A
a
r
= (10) (10) = 0
Also
BA
v
r
=
B
v
r
A
v
r
= 10 5 = 5 m/s
BA
s
r
(in 1 sec) =
BA
v
r
t = 5 1 = 5 m
Distance between A and B after 1 sec = 5 m.
Illustration :
A ball is thrown downwards with a speed of 20 m/s from top of a building 150 m
high and simultaneously another ball is thrown vertically upwards with a speed
of 30 m/s from the foot of the building. Find the time when both the balls will
meet. (g = 10 m/s
2
)
Sol. (I) S
1
= 20 t + 5 t
2
+ S
2
= 30 t 5 t
2
____________________
150 = 50 t
t = 3 s.
(II) Relative acceleration of both is zero since both have acceleration in downward direction
AB
a
r
=
A
a
r
B
a
r
= g g = 0
BA
v
r
= 30 (20)
= 50
s
BA
= v
BA
t
t =
BA
BA
v
s
=
50
150
= 3 s
RESONANCE Page # 22 Page # 22 Page # 22 Page # 22 Page # 22
TM
Ex.5 Two cars C
1
and C
2
moving in the same direction on a straight road with velocities 12 m/s and 10 m/s
respectively. When the separation between the two was 200 m C
2
started accelerating to avoid collision.
What is the minimum acceleration of car C
2
so that they dont collide.
Sol. By relative
2 1
C C
a
r
=
1
C
a
r
2
C
a
r
= 0 a = (a)
2 1
C C
v
r
=
1
C
v
r
2
C
v
r
= 12 10 = 2 m/s.
So by relativity we want the car to stop.
v
2
u
2
= 2as.
0 2
2
= 2 a 200 a =
100
1
m/s
2
= 0.1 m/s
2
= 1 cm/s
2
.
Minimum acceleration needed by car C
2
= 1 cm/s
2
RELA RELA RELA RELA RELATIVE MO TIVE MO TIVE MO TIVE MO TIVE MOTION IN LIFT TION IN LIFT TION IN LIFT TION IN LIFT TION IN LIFT
Illustration :
A lift is moving up with acceleration a. A person inside the lift throws the
ball upwards with a velocity u relative to hand.
(a) What is the time of flight of the ball?
(b) What is the maximum height reached by the ball in the lift?
Sol. (a)
BL
a
r
=
B
a
r
L
a
r
= (g + a) downwards
s
r
= u
r
t +
2
1
BL
a
r
t
2
0 = uT
2
1
(g + a)T
2
T =
) a g (
u 2
+
(b) v
2
u
2
= 2 as 0 u
2
= 2(g + a) H
H =
) a g ( 2
u
2
+
Projectile motion in a lift moving with acceleration a upwards Projectile motion in a lift moving with acceleration a upwards Projectile motion in a lift moving with acceleration a upwards Projectile motion in a lift moving with acceleration a upwards Projectile motion in a lift moving with acceleration a upwards
(1) Initial velocity = u
(2) Velocity at maximum height = u cos
(3) T =
a g
sin u 2
+
(4) Maximum height (H) =
) a g ( 2
sin u
2 2
+
(5) Range =
a g
2 sin u
2
+
RESONANCE Page # 23 Page # 23 Page # 23 Page # 23 Page # 23
TM
RELA RELA RELA RELA RELATIVE MO TIVE MO TIVE MO TIVE MO TIVE MOTION IN T TION IN T TION IN T TION IN T TION IN TW WW WWO DIMENSION O DIMENSION O DIMENSION O DIMENSION O DIMENSION
A
r
r
= position of A with respect to O
B
r
r
= position of B with respect to O
AB
r
r
= position of A with respect to B.
B A AB
r r r
r r r
=
dt
) r ( d
AB
r
=
dt
) r ( d
A
r
dt
) r ( d
B
r
.
B A AB
v v v
r r r
=
dt
) v ( d
AB
r
=
dt
) v ( d
A
r
dt
) v ( d
B
r
B A AB
a a a
r r r
=
Note : These formulae are not applicable for light.
Illustration :
Object A and B has velocities 10 m/s. A is moving along East while B is moving towards North from the same
point as shown. Find velocity of A relative to B (
AB
v
r
)
Sol.
AB
v
r
=
A
v
r
B
v
r
AB
v
r
= 102
Note :
B A
v v
r r
=
+ cos v v 2 v v
B A
2
B
2
A
Illustration :
Two particles A and B are projected in air. A is thrown horizontally, B is thrown
vertically up. What is the separation between them after 1 sec.
Sol.
AB
a
r
=
A
a
r
B
a
r
= 0
AB
v
r
=
2 2
10 10 +
=
2 10
s
AB
= v
AB
t = (10 2 ) t = 10 2 m
Consider the situation, shown in figure
RESONANCE Page # 24 Page # 24 Page # 24 Page # 24 Page # 24
TM
Ex.23 (i) Find out velocity of B with respect to A
A B BA
v v v
r r r
= = 20 j
20 i
(ii) Find out velocity of A with respect to B
B A AB
v v v
r r r
= = 20 i
20 j
Ex.24
(1) Find out motion of tree, bird and old man as seen by boy.
(2) Find out motion of tree, bird, boy as seen by old man
(3) Find out motion of tree, boy and old man as seen by bird.
Sol. (1) With respect to boy :
v
tree
= 16 m/s ()
v
bird
= 12 m/s ()
v
old man
= 18 m/s ()
(2) With respect to old man :
v
Boy
= 18 m/s ()
v
Tree
= 2 m/s ()
v
Bird
= 18 m/s () and 12 m/s ()
(3) With respect to Bird :
v
Tree
= 12 m/s () and 16 m/s ()
v
old man
= 18 m/s () and 12 m/s ().
v
Boy
= 12 m/s ().
MO MO MO MO MOTION OF A TRAIN MO TION OF A TRAIN MO TION OF A TRAIN MO TION OF A TRAIN MO TION OF A TRAIN MOVING ON EQU VING ON EQU VING ON EQU VING ON EQU VING ON EQUA AA AAT TT TTOR : OR : OR : OR : OR :
If a train is moving at equator on the earths surface with a velocity v
TE
relative to earths surface and a point
on the surface of earth with velocity v
E
relative to its centre, then
E T TE
v v v
r r r
= or
E TE T
v v v
r r r
+ =
So, if the train moves from west to east and if the train moves from east to west
(the direction of motion of earth on its axis) (i.e. opposite to the motion of earth)
RESONANCE Page # 25 Page # 25 Page # 25 Page # 25 Page # 25
TM
v
T
= v
TE
+ v
E
v
T
= v
TE
v
E
Relative Motion on a moving traing :
If a boy is running with speed
BT
v
r
on a train moving with velocity
T
v
r
relative to ground, the speed of the boy
relative to ground
B
v
r
will be given by:
BT
v
r
=
B
v
r
T
v
r
or
B
v
r
=
BT
v
r
+
T
v
r
so, if the boy is running in the direction of train
v
B
= u + v
and if the boy is running on the train in a direction opposite to the motion of train
v
B
= u v
RELA RELA RELA RELA RELATIVE MO TIVE MO TIVE MO TIVE MO TIVE MOTION IN RIVER FL TION IN RIVER FL TION IN RIVER FL TION IN RIVER FL TION IN RIVER FLO OO OOW W W W W :
If a man can swim relative to water with velocity
mR
v
r
and water is following relative to ground with velocity
R
v
r
, velocity of man relative to ground
m
v
r
will be given by :
mR
v
r
=
m
v
r
R
v
r
or
m
v
r
=
mR
v
r
+
R
v
r
So, if the swimming is in the direction of flow of water,
v
m
= v
mR
+ v
R
and if the swimming is opposite to the flow of water,
v
m
= v
mR
v
R
Illustration :
A swimmer capable of swimming with velocity v relative to water jumps in a flowing river having velocity u. The
man swims a distance d down stream and returns back to the original position. Find out the time taken in
complete motion.
Sol. t = t
down
+ t
up
=
u v
d
+
+
u v
d
=
2 2
u v
dv 2
Ans.
RESONANCE Page # 26 Page # 26 Page # 26 Page # 26 Page # 26
TM
CROSSING RIVER CROSSING RIVER CROSSING RIVER CROSSING RIVER CROSSING RIVER
A boat or man in a river always moves in the direction of resultant velocity of velocity of boat (or man) and
velocity of river flow.
1. Shortest Time :
The person swims perpendicular to the river flow crossing a river : consider a river having flow velocity
R
v
r
and
swimmer jump into the river from a point A, from one bank of the river, in a direction perpendicular to the
direction of river current. Due to the flow velocity of river the swimmer is drifted along the river by a distance
BC and the net velocity of the swimmer will be
m
v
r
along the direction AC.
If we find the components of velocity of swimmer along and perpendicular to the flow these are.
Velocity along the river, v
x
= v
R
.
Velocity perpendicular to the river, v
f
= v
mR
<
The net speed is given by v
m
=
2
R
2
mR
v v +
v
r
d
y
B
drift = x
x
v
m
v
mR
A
C
at an angle of tan =
R
mR
v
v
(down stream with the direction of flow).
Velocity of v
y
is used only in crossing the river, time taken to cross the river is t =
mR y
v
d
v
d
=
.
Velocity v
x
is only used to drift the motion of the swimmer in the river,
drift is along the river flow,
x = (v
x
) (t) or x = v
R
mR
v
d
Illustration :
A river 400 m wide is flowing at a rate of 2.0 m/s.A boat is sailing at a velocity of 10 m/s with respect to the
water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank.
(c) In what direction does the boat actually move.
Sol.
(a) time taken to cross the river
t =
y
v
d
=
s / m 10
m 400
= 40 s Ans.
(b) drift (x) = (v
x
)(t) = (2m/s) (40s) = 80 m Ans.
(c) Actual direction of boat,
= tan
1
2
10
= tan
1
5, (downstream) with the river flow.
RESONANCE Page # 27 Page # 27 Page # 27 Page # 27 Page # 27
TM
2. 2. 2. 2. 2. SHORTEST PA SHORTEST PA SHORTEST PA SHORTEST PA SHORTEST PATH : TH : TH : TH : TH :
When the person crosses the river perpendicularly (along the shortest path). It should swim up stream
making an angle with AB such that the resultant velocity
m
v
r
, of man must be perpendicular to the flow of
river along AB.
If we find the components of velocity of swimmer along and perpendicular to the flow, these are,
velocity along the river, v
x
= 0
and velocity perpendicular to river v
y
=
2
R
2
mR
v v
The net speed is given by v
m
=
2
R
2
mR
v v
at an angle of 90 with the river direction.
velocity v
y
is used only to cross the river, therefore time to cross the river, t =
y
v
d
=
2
R
2
mR
v v
d
and velocity v
x
is zero, therefore, in this case the drift (x) should be zero.
x = 0
or v
x
= v
R
v
mR
sin = 0
or v
R
= v
mR
sin
or = sin
1
mR
R
v
v
Hence, to cross the river perpendicular (along the shortest path) the man should swim at an angle of
mR
R 1
v
v
sin
2
upstream from the direction of river flow.
further, since sin < 1,
Swimmer can cross the river perpendicularly only when v
mR
> v
R
ie
Practically it is not possible to reach at B if the river velocity (v
R
) is too high.
Illustration :
A man can swim at the rate of 5 km/h in still water. A river 1 km wide flows at the rate of 3 km/h. The man
wishes to swim across the river directly opposite to the starting point.
(a) Along what direction must the man swim?
(b) What should be his resultant velocity?
(c) How much time the would take to cross?
Sol. The velocity of man with respect to river v
mR
= 5 km/hr, this is greater than the river flow velocity, therefore, he
can cross the river directly (along the shortest path). The anlge of swim must be
=
2
+ sin
1
mR
r
v
v
= 90 + sin
-1
mR
r
v
v
= 90 + sin
1
5
3
= 90 + 37 = 127, with the river flow (upstream) Ans.
RESONANCE Page # 28 Page # 28 Page # 28 Page # 28 Page # 28
TM
(b) Resultant velocity will be v
m
=
2
R
2
mR
v v
=
2 2
3 5
= 4 km/hr
along the direction perpendicular to the river flow.
(c) time taken to cross the
t =
2
R
2
mR
v v
d
=
hr / km 4
km 1
=
4
1
h = 15 min
Ex. The velocity of about in still water is 5 km/h it crosses 1 km wide river in 15 minutes along the shortest
possible path. Determine the velocity of water in the river in km/h
Ans. 3km/h
Illustration :
A man wishes to cross a river flowing with velocity u jumps at an anlge with the river flow. Find out the net
velocity of the man with respect to ground if he can swim with speed v. Also find
How far from the point directly opposite to the starting point does the boat reach the opposite bank. in what
direction does the boat actually move. If the width of the river is d.
Sol. Velocity of man = v
M
= + + cos u v 2 v u
2 2
Ans.
tan =
+
cos v u
sin v
Ans.
(v sin) t = d t =
sin v
d
x = (u + v cos ) t = (u + v cos)
sin v
d
Ans.
Illustration :
A boat moves relative to water with a velocity which is n times less than the river flow velocity. At what anlge
to the stream direction must the boat move to minimize drifting?
Sol. In this problem, one thing should be carefully meted that
the velocity of boat is less than the river flow velocity. In
such a case, boat cannot reach the point directly oppo-
site to its starting point. i.e. drift can never be zero. Thus,
to minimize the drift, boat starts at an angle from the
normal direction up stream as shown.
Now, again if we find the components of velocity of boat along and perpendicular to the flow, these are,
velocity along the river, v
x
= u v sin .
and velocity perpendicular to the river, v
y
= v cos .
time taken to cross the river is t =
y
v
d
=
cos v
d
.
In this time, drift x = (v
x
)t
= (u v sin )
cos v
d
or x =
v
ud
sec d tan
The drift x is minimum, when
d
dx
= 0,
RESONANCE Page # 29 Page # 29 Page # 29 Page # 29 Page # 29
TM
or
v
ud
(sec . tan ) d sec
2
= 0
or
v
u
sin = 1
or sin =
u
v
=
n
1
(as v =
n
u
)
so, for minimum drift, the boat must move at an angle = sin
1
u
v
from normal direction or
an angle
2
+ sin
1
u
v
from stream direction.
RAIN PROBLEMS RAIN PROBLEMS RAIN PROBLEMS RAIN PROBLEMS RAIN PROBLEMS
If rain is falling vertically with a velocity
R
v
r
and on observer is moving horizontally with velocity
m
v
r
, the
velocity of rain relative to observer will be :
Rm
v
r
=
R
v
r
m
v
r
or v
Rm
=
2
m
2
R
v v +
and direction = tan
1
R
m
v
v
with the vertical as shown in figure.
Illustration :
Rain is falling vertically and a man is moving with velocity 6 m/s. Find the angle with which umbrella should
be hold by man to avoid getting wet.
Sol.
v
r
rain
= 10 j
v
r
man
= 6 i
Velocity of rain with respect to man =
v
r
r m
= 10 j
6 i
tan =
10
6
= tan
1
5
3
Where is angle with vertical
RESONANCE Page # 30 Page # 30 Page # 30 Page # 30 Page # 30
TM
Illustration :
A man moving with 5m/s observes rain falling vertically at the rate of 10 m/s. Find the speed and direction of
the rain with respect to ground.
v
RM
= 10 m/s, v
M
= 5 m/s
RM
v
r
=
Ru
v
r
M
v
r
Ru
v
r
=
RM
v
r
M
v
r
R
v
r
=
5 5
tan =
2
1
, = tan
1
2
1
.
Illustration :
A man standing, observes rain falling with velocity of 20 m/s at an angle of 30 with the vertical.
(1) Find out velocity of man so that rain appears to fall vertically.
(2) Find out velocity of man so that rain again appears to fall at 30 with the vertical.
Sol. (1)
m
v
r
= v i
(let)
R
v
r
= 10 i
103 j
RM
v
r
= (10 v) i
103 j
(10 v) = 0 (for vertical fall, horizontal component must be zero)
or v = 10 m/s Ans.
(2)
R
v
r
= 10 i
103 j
m
v
r
= v
x
i
RM
v
r
= (10 v
x
) i
103 j
Angle with the vertical = 30
tan 30 =
3 10
v 10
x
v
x
= 20 m/s
RESONANCE Page # 31 Page # 31 Page # 31 Page # 31 Page # 31
TM
WIND AIRPLANE WIND AIRPLANE WIND AIRPLANE WIND AIRPLANE WIND AIRPLANE
This is very similar to boat river flow problems the only difference is that boat is replaced by also plane and
river is replaced by wind.
Thus,
velocity of aeroplane with respect to wind
w a aw
v v v
r r r
=
or
w aw a
v v v
r r r
+ =
where,
a
v
r
= absolute velocity of aeroplane
and,
w
v
r
= velocity of wind.
Illustration :
An aeroplane flies along a straight path A to B and returns back again. The distance between A and B is l
and the aeroplane maintains the constant speed v. There is a steady wind with a speed u at an angle with
line AB. Determine the expression for the total time of the trip.
Sol. A to B :
Velocity of plane along AB = v cos ucos ,
and for no-drift from line
AB : v sin = usin sin =
v
sin u
time taken from A to B : t
AB
=
cos u cos v
l
B to A :
velocity of plane along BA = vcos + u cos
and for no drift from line AB : vsin = usin
sin =
v
sin u
time taken from B to A : t
BA
=
+ cos u cos v
l
total time taken = t
AB
+ t
BA
=
+ cos u cos v
l
+
+ cos u cos v
l
=
+
2 2 2 2
cos u cos v
cos v 2 l
=
2 2
2
2 2
u v
v
sin u
1 v 2
l
.
Ex. Find the time an aeroplane having velocity v, take to fly around a square with side a and the wind blowing at
a velocity u, in the two cases,
(a) if the direction of wind is along one side of the square,
(b) If the direction of wind is along one of the diagonals of the square
Ans. (a)
2 2
u v
a 2
+
2 2
u v v
(b) a 2 2
2 2
2 2
u v
u v 2
.
RESONANCE Page # 32 Page # 32 Page # 32 Page # 32 Page # 32
TM
Condition to collide or to reach at the same point Condition to collide or to reach at the same point Condition to collide or to reach at the same point Condition to collide or to reach at the same point Condition to collide or to reach at the same point
When the relative velocity of one particle w.r.t. to other particle is directed towards each other then they will
collide. (If there is a zero relative acceleration).
Illustration :
There are particles A, B and C are situated at the vertices of an equilateral triangle ABC of side a at t = 0.
Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C
along CA. At what time will the particle meet each other?
Sol. The motion of the particles is roughly sketched in figure. By symmetry they will meet at the centroid O of the
triangle. At any instant the particles will from an equilateral triangle ABC with the same
Centroid O. All the particles will meet at the centre. Concentrate on the motion of any one particle, say B.
At any instant its velocity makes angle 30 with BO.
The component of this velocity along BO is v cos 30. This component is the rate of decrease of the distance
BO. Initially.
BO =
30 cos
2 / a
=
3
a
= displacement of each particle.
Therefore, the time taken for BO to become zero
=
30 cos v
3 / d
=
3 v 3
d 2
=
v 3
d 2
.
Alternative : Velocity of B is v along BC. The velocity of C is along CA. Its
component along BC is v cos 60 = v/2. Thus, the separation BC de-
creases at the rate of approach velocity.
approach velocity = v +
2
v
=
2
v 3
Since, the rate of approach is constant, the time taken in reducing the separation BC from a to zero is
t =
v 3
a 2
2
v 3
a
=
Q. Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle
maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet
each other.
Ans. 2 a/v.
Q. A moves with constant velocity u along then x axis. B always has veloc-
ity towards A. After how much time will B meet A if B moves with constant
speed v. What distance will be travelled by A and B.
Ans. distance travelled by A =
2 2
2
u v
v
l
,
distance travelled by B =
2 2
u v
uv
l
RESONANCE Page # 33 Page # 33 Page # 33 Page # 33 Page # 33
TM
Illustration :
Two cars A and B are moving west to east and south to north respectively along crossroads. A moves with a
speed of 72 kmh
1
and is 500 m away from point of intersection of cross roads and B moves with a speed of
54 kmh
1
and is 400 m away from point of intersection of cross roads. Find the shortest distance between
them ?
Sol.
Method I (Using the concept of relative velocity)
In this method we watch the velocity of A w.r.t. B. To do this we plot the resultant velocity V
r
. Since the
accelerations of both the bodies is zero, so the relative acceleration between them is also zero. Hence the
relative velocity will remain constant. So the path of A with respect to B will be straight line and along the
direction of relative velocity of A with respect to B. The shortest distance between A & B is when A is at point
F (i.e. when we drop a perpendicular from B on the line of motion of A with respect to B).
From figure
tan =
A
B
V
V
=
20
15
=
4
3
........................(i)
This is the angle made by the resultant velocity vector with the x-axis.
Also we know that from figure
OE =
500
x
=
4
3
..............................(ii)
From equation (i) & (ii) we get
x = 375 m
EB = OB OE = 400 375 = 25 m
But the shortest distance is BF.
From magnified figure we see that BF = EB cos = 25
5
4
BF = 20 m
Method II (Using the concept of maxima minima)
A & B be are the initial positions and A,B be the final positions after time t.
B is moving with a speed of 15 m/sec so it will travel a distance of BB = 15t during time t.
A is moving with a speed of 20 m/sec so it will travel a distance of AA = 20t during time t.
So
OA =500 20 t
OB = 400 15 t
AB
2
= OA
2
+ OB
2
= (500 20t)
2
+ (400 15t)
2
..................(i)
For AB to be minimum AB
2
should also be minimum
RESONANCE Page # 34 Page # 34 Page # 34 Page # 34 Page # 34
TM
dt
) ' B ' A ( d
2
=
dt
) t 20 500 ( ) t 15 400 ( d
2 2
+
= 0
= 2(400 15t) (15) + 2(500 20t) (20) = 0
= 1200 + 45t = 2000 80 t
125 t = 3200
t =
5
128
s. Hence A and B will be closest after
5
128
s.
Now
2
2
dt
' B ' A d
comes out to be positive hence it is a minima.
On substituting the value of t in equation (i) we get
AB
2
=
2
5
128
15 400
+
2
5
128
. 20 500
=
2 2
) 12 ( 16 + = 20 m
Minimum distance AB = 20 m.
Method III (Using the concept of relative velocity of approach)
After time t let us plot the components of velocity of A & B in the
direction along AB. When the distance between the two is mini-
mum, the relative velocity of approach is zero.
V
A
cos
f
+ V
B
sin
f
= 0
(where
f
is the angle made by the line AB with the x-axis)
20 cos
f
= 15 sin
f
tan
f
=
15
20
=
3
4
Here do not confuse this angle with the angle in method (I)
because that is the angle made by the resultant with x-axis.
Here
f
is the angle made with x-axis when velocity of approach in zero,
t 20 500
t 15 400
=
3
4
t =
5
128
So, OB = 16 m and OA = 12m
AB =
2 2
) 12 ( 16 + = 20 m
Qus. Two ships are 10 km apart on a line running south to north. The one farther north is steaming west at
20 km h
1
. The other is steaming north at 20 km h
1
. What is their distance of closest approach ? How long
do they take to reach it ?
Ans.
2 5
km/h ; 1/4 h = 15 min consider the situation shown in figure for the two particle A and B.
Qus. (1) Will the two particle will collide
(2) Find out shortest distance between two particles
Ans. (1) The particles will not collide
(2)
5 4
m.
Note : Muzzle Velocity is the velocity of bullet with respect to the gun i.e. it is Relative Velocity.
RESONANCE Page # 35
TM
Exercise 1
OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS
1. A stone is thrown upwards with a velocity 50 ms
1
. Another stone is simultaneously thrown downwards from
the same location with a velocity 50 ms
1
. When the first stone is at the highest point, the relative velocity of
the second stone w.r.t. the first stone is :
(A) Zero (B) 50 ms
1
(C) 100 ms
1
(D) 150 ms
1
2. A thief is running away on a straight road in a jeep moving with a speed of 9 m s
1
. A police man chases him
on a motor cycle moving at a speed of 10 m s
1
. If the instantaneous separation of the jeep from the
motorcycle is 100m, how long will it take for the police man to catch the thief?
(A) 1s (B) 19s (C) 90s (D) 100s
3. Two cars are moving in the same direction with a speed of 30 km h
1
. They are separated from each other by
5 km. Third car moving in the opposite direction meets the two cars after an interval of 4 minutes. What is the
speed of the third car?
(A) 30 km h
1
(B) 35 km h
1
(C) 40 km h
1
(D) 45 km h
1
4. Shown in the figure are the displacement time graph for two children going home from the school. Which of
the following statements about their relative motion is true?
Their relative velocity :
(A) first increases and then decreases
(B) first decreases and then increases
(C) is zero
(D) is non zero constant.
5. A person standing on the escalator takes time t
1
to reach the top of a tower when the escalator is moving. He
takes time t
2
to reach the top of the tower when the escalator is standing. How long will he take if he walks
up a moving escalator?
(A) t
2
t
1
(B) t
1
+ t
2
(C) t
1
t
2
/(t
1
t
2
) (D) t
1
t
2
/(t
1
+ t
2
)
6. Shown in the figure are the velocity time graphs of the two particles P
1
and P
2
. Which of the following
statements about their relative motion is true?
Their relative velocity :
(A) is zero
(B) is non-zero but constant
(C) continuously decreases
(D*) continuously increases
7. Two particles P
1
and P
2
are moving with velocities v
1
and v
2
respectively. Which of the statement about their
relative velocity v
r 12
is true?
(A) v
r 12
> (v
1
+ v
2
) (B) v
r 12
cannot be greater than v
1
v
2
(C) v
r 12
cannot be greater than v
1
+ v
2
(D) v
r 12
< (v
1
+ v
2
)
8. Two identical trains take 3 sec to pass one another when going in the opposite direction but only
2.5 sec if the speed of one is increased by 50 %. The time one would take to pass the other when going
in the same direction at their original speed is :
(A) 10 sec (B) 12 sec (C) 15 sec (D) 18 sec
9. Two billiard balls are rolling on a flat table. One has velocity components v
x
= 1m/s, v
y
=
3
m/s and the other
has components v
x
= 2m/s and v
y
= 2 m/s. If both the balls start moving from the same point, the angle
between their path is -
(A) 60 (B) 45 (C) 22.5 (D*) 15
10. A battalion of soldiers is ordered to swim across a river 500 ft wide . At what minimum rate should they
swim perpendicular to river flow in order to avoid being washed away by the waterfall 300 ft downstream.
The speed of current being 3 m.p.h. :
(A) 6 m.p.h. (B*) 5 m.p.h. (C) 4 m.p.h. (D) 2 m.p.h.
11. A boat, which has a speed of 5 km/hr in still water, crosses a river of width 1 km along the shortest possible
path in 15 minutes. The velocity of the river water in km/hr is -
(A) 1 (B*) 3 (C) 4 (D) 41
RESONANCE Page # 36
TM
12. A bucket is placed in the open where the rain is falling vertically. If a wind begins to blow at double the velocity
of the rain, how will be rate of filling of the bucket change?
(A) Remain unchanged (B) Doubled (C) Halved (D) Become four times
13. A car with a vertical wind shield moves along in a rain storm at the speed of 40 km/hr. The rain drops fall
vertically with a terminal speed of 20 m/s. The angle with the vertical at which the rain drop strike the wind
shield is -
(A) tan
1
(5/9) (B) tan
1
(9/5) (C) tan
1
(3/2) (D) tan
1
(3)
SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS
14. Men are running along a road at 15 km/h behind one another at equal intervals of 20 m. Cyclist are
riding in the same direction at 25 km/h at equal intervals of 30 m. At what speed an observer travel
along the road in opposite direction so that whenever he meets a runner he also meets a cyclist?s
15. Two perpendicular rail tracks have two trains A & B respectively. Train A moves north with a speed of 54 km
h
1
and train B moves west with a speed of 72 km h
1
. Assume that both trains starts from same point.
Calculate the
(a) rate of separation of the two trains
(b) relative velocity of ground with respect to B
(c) relative velocity of A with respect to B.
16. A man is swimming in a lake in a direction of 30East of North with a speed of 5 km/hr and a cyclist is
going on a road along the lake shore towards East at a speed of 10 km/hr. In what direction and with
what speed would the man appear to swim to the cyclist.
17. A motor boat has 2 throttle position on its engine. The high speed position propels the boat at 10 km
hr
1
in still water and the low position gives half the higher speed. The boat travels from its dock
downstream on a river with the throttle at low position and returns to its dock with throttle at high
position. The return trip took 15
% longer time than it did for the downstream trip. Find the velocity of
the water current in the river.
18. () A man can swim with a speed of 4 km h
1
in still water. How long does he take to cross a river 1 km wide
if the river flows steadily at 3 km h
1
and he makes his strokes normal to the river current ? How far down the
river does he go when he reaches the other bank ?
() If he keeps himself always at an angle of 120C with the river flow while swimming.
(a) Find the time he takes to cross the river. (b) At what point on the opposite bank will he arrive ?
19. A river is flowing from west to east at a speed of 5 m/min. A man on the south bank of the river, capable of
swimming at 10 m/min in still water, wants to swim across the river in shortest distance. In what direction
should he swim ?
20. An airplane is flying with velocity
2 50
km/hour in north-east direction. Wind is blowing at 25 km/hr from
north to south. What is the resultant displacement of airplane in 2 hours ?
21. When a train has a speed of 10 m s
1
eastward, raindrops that are falling vertically with respect to the earth
make traces that are inclined 30 to the vertical on the windows of the train.
(a) What is the horizontal component of a drop's velocity with respect to the earth ? With respect to the train ?
(b) What is the velocity of the raindrop with respect to the earth ? With respect to the train ?
22. To a man walking at 7 km/h due west, the wind appears to blow from the north-west, but when he walks at 3
km/h due west, the wind appears to blow from the north. What is the actual direction of the wind and what is
its velocity ?
23. When a motorist is driving with velocity j
8 i
6 + , the wind appears to come from the direction i
. When
he doubles his velocity the wind appears to come from the direction j
+ . Then the true velocity of the
wind expressed in the form of j
b i
a + is ______.
24. '
n
' numbers of particles are located at the vertices of a regular polygon of '
n
' sides having the edge
length '
a
'. They all start moving simultaneously with equal constant speed '
v
' heading towards each
other all the time. How long will the particles take to collide?
25. Two ships are 10 km apart on a line running south to north. The one further north is streaming west at
40 km/hr. The other is streaming north at 40 km/hr. What is their distance of closest approach and how
long do they take to reach it?
RESONANCE Page # 37
TM
26. A ship is sailing towards north at a speed of 2 m/s. The current is taking it towards East at the rate
of 1 m/s and a sailor is climbing a vertical pole on the ship at the rate of 1 m/s. Find the velocity of the
sailor in space.
27. A motorboat is observed to travel 10 km hr
1
relative to the earth in the direction 37 north of east. If the
velocity of the boat due to the wind only is 2 km hr
1
westward and that due to the current only is 4 km hr
1
southward, what is the magnitude and direction of the velocity of the boat due to its own power ?
28. A person P sitting on a wooden block (which does not move relative to water) in a flowing river sees two
swimmers A and B. A and B both have constant speed v
m
relative to water. P observes that A starts from
one point of the river bank and appears to move perpendicular to the river flow. P also observes that B
starts from some point on the other bank at the same time and moves downstream. The width of the
river is '
d
' and it flows with velocity v
r
. If A and B both reach a point at the same time, than find the initial
separation between A and B.
29. A motorboat going down stream overcome a float at a point M. 60 minutes later it turned back and after
some time passed the float at a distance of 6 km from the point M. Find the velocity of the stream
assuming a constant velocity for the motorboat in still water.
30. 2 swimmers start from point A on one bank of a river to reach point B on the other bank, lying directly
opposite to point A. One of them crosses the river along the straight line AB, while the other swims at
right angles to the stream and then walks the distance which he has been carried away by the stream
to get to point B. What was the velocity (assumed uniform) of his walking if both the swimmers
reached point B simultaneously. Velocity of each swimmer in still water is 2.5 km hr
1
and the stream
velocity is 2 km hr
1
.
31. An airplane pilot sets a compass course due west and maintains an air speed of 240 km. hr
1
. After flying for
2
1
hr, he finds himself over a town that is 150 km west and 40 km south of his starting point.
(a) Find the wind velocity, in magnitude and direction.
(b) If the wind velocity were 120 km. hr
1
due south, in what direction should the pilot set his course in
order to travel due west ? Take the same air speed of 240 km. hr
1
.
32. Two straight AOB and COD meet each other right angles. A person walking at a speed of 5 km/hr
along AOB is at the crossing O at noon. Another person walking at the same speed along COD reaches
the crossing O at 1:30 PM. Find at what time the distance between them is least and what is its value?
1. An aeroplane is flying vertically upwards with a uniform speed of 500 m/s. When it is at a height of
1000 m above the ground a shot is fired at it with a speed of 700 m/s from a point directly below it.
What should be the acceleration of the aeroplane so that it may escape from being hit?[REE 94, 6 ]
2. The width of a river is 25 m and in it water is flowing with a velocity of 4 m/min. A boatman is standing
on the bank of the river. He wants to sail the boat to a point at the other bank which is directly opposite
to him. In what time will he cross the river, if he can sail the boat at 8 m/min, relative to the water.
[ REE '95, 6 ]
3. On a frictionless horizontal surface, assumed to be the x
y plane a small trolley A is moving along a
straight line parallel to the y
axis as shown in the figure with a constant velocity of ( 3 1) m/s.
At
a particular instant, when the line OA makes an angle of 45 with the x
axis, a ball is thrown along the
surface from the origin O. Its velocity makes an angle
with the x
axis when it hits the trolley.
(a) The motion of the ball is observed from the frame of the trolley.
Calculate the angle made by the velocity of the ball with
the x
axis in this frame.
(b) Find the speed of the ball with respect to the surface, if = 4
/3.
[ JEE 2002, 2 + 3 ]
RESONANCE Page # 38
TM
EXERCISE # 1 EXERCISE # 1 EXERCISE # 1 EXERCISE # 1 EXERCISE # 1
OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS
1. C 2. D 3. D 4. D
5. D 6. D 7. C 8. C
9. D 10. B 11. B 12. A
13. A
SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS
14. 5 km/h
15. (a) 25 m/s or 90 km/hr (b) 20 m/s or 72 km/hr due
east (c) 25 m/s or 90 km/hr at 37N of E
16. 30 N of W at 3 5 km/hr. 17. 3 km/hr.
18. () 0.75 km
() (a)
3 2
1
h (b)
3 2
1
km.
19. At an angle 30west of north.
20. km 5 50
21. (a) 0, 10 m/s West (b) 10
3
m/s, 20 m/s
22. Coming from 5 km/hr, 53N of E
23. ( ) j
8 i
4 + 24.
n
2
cos 1 v
a
25.
2
10
,
8
1
hr
26. 2m/s in a direction making an angle of 60 with E,
45 with N and 60 with the vertical
27.
2 10
km/hr, 45 N of E
28. 2 d 29. 3 km/hr
30. 3 km/hr towards B
31. (a) 100 km/hr, 37 W of S (b) 30 N of W
32. 12 : 45 PM
EXERCISE # 2 EXERCISE # 2 EXERCISE # 2 EXERCISE # 2 EXERCISE # 2
1. a > 10 m/s
2
2. 3.6 minute
3. (a) = 45 ; (b) 2 m/s
RESONANCE Page # 39 Page # 39 Page # 39 Page # 39 Page # 39
TM
I mentally conceive of some
movable projected on a hori-
zontal plane all impediments
being put aside. Now it is
evident ... that the equable
motion on this plane would
be perpetual if the plane were
of infinite extent; but if we
assume it to be ended, and
[situated] on high, the mov-
able ... , driven to the end of
the plane and going on fur-
ther, adds on to its previous
equable and indelible motion
that downward tendency
which it has from its own
heaviness. Thus there emerges
a certain motion, compounded
from equable horizontal and
from naturally accelerated
downward [motion], which I
call projection.
- Galileo
(Two New Sciences 1638)
PR PR PR PR PROJECTILE MO OJECTILE MO OJECTILE MO OJECTILE MO OJECTILE MOTION TION TION TION TION
1. 1. 1. 1. 1. BASIC CONCEPT : BASIC CONCEPT : BASIC CONCEPT : BASIC CONCEPT : BASIC CONCEPT :
1.1 PROJECTILE
Any object that is given an initial velocity obliquely and that subse-
quently follows a path determined by the gravitational force acting on
it, is called a Projectile. A projectile may be a football, a cricket ball,
or any other object.
1.2 TRAJECTORY
The path followed by a particle (here projectile) during its motion is
called its Trajectory.
NOTE : 1. We shall consider only trajectories that are of sufficiently
short range so that the gravitational force can be considered constant
in both magnitude and direction.
2. All effects of air resistance will be ignored; thus our results are
precise only for motion in a vacuum on flat, non rotating Earth.
1.3 PROJECTILE MOTION
(i) The motion of projectile is known as projectile motion.
(ii) It is an example of two dimensional motion with constant
acceleration.
(iii) Projectile motion is considered as combination of two simultaneous
motions in mutually perpendicular directions which are completely
independent from each other i.e. horizontal motion and vertical motion.
= +
Parabolic path = vertical motion + horizontal motion.
RESONANCE Page # 40 Page # 40 Page # 40 Page # 40 Page # 40
TM
2. 2. 2. 2. 2. PR PR PR PR PROJECTILE THR OJECTILE THR OJECTILE THR OJECTILE THR OJECTILE THRO OO OOWN A WN A WN A WN A WN AT AN ANGLE WITH HORIZONT T AN ANGLE WITH HORIZONT T AN ANGLE WITH HORIZONT T AN ANGLE WITH HORIZONT T AN ANGLE WITH HORIZONTAL AL AL AL AL
(i) Consider a projectile thrown with a velocity u making an angle with the horizontal.
(ii) Initial velocity u is resolved in components in a coordinate system in which horizontal direction is
taken as x-axis, vertical direction as y-axis and point of projection as origin.
u
x
= u cos
u
y
= u sin
(iii) Again this projectile motion can be considered as the combination of horizontal and vertical motion.
Therefore,
Horizontal direction Vertical direction
(a) Initial velocity u
x
= u cos Initial velocity u
y
= u sin
(b) Acceleration a
x
= 0 Acceleration a
y
= g
(c) Velocity after time t, v
x
= u cos Velocity after time t,v
y
= u sin gt
2.1 TRAJECTORY EQUATION : If we consider the horizontal direction,
x = u
x
.t
x = u cos . t ...(1)
For vertical direction :
y = u
y
. t 1/2 gt
2
= u sin . t 1/2 gt
2
...(2)
Substituting the value x equation (1)
y = u sin .
cos u
x
2
1
g
2
cos u
x
This is an equation of parabola called as trajectory equation of projectile motion.
2.2 TIME OF FLIGHT : Since the displacement along vertical direction does not occur. So,
Net displacement = 0
(u sin ) T
2
1
gT
2
= 0
T =
g
sin u 2
RESONANCE Page # 41 Page # 41 Page # 41 Page # 41 Page # 41
TM
2.3 HORIZONTAL RANGE :
R = u
x
.T
R = u cos .
g
sin u 2
R =
g
2 sin u
2
2.4 MAXIMUM HEIGHT :
Using 3
rd
equation of motion i.e.
v
2
= u
2
+ 2as
we have for vertical direction
0 = u
2
sin
2
2gH
H =
g 2
sin u
2 2
2.5 RESULTANT VELOCITY :
j
v i
v v
y x
+ =
r
= u cos i
+ (u sin gt) j
where |
v
v
| =
2 2 2
) gt sin u ( cos u + and tan = v
y
/ v
x
.
NOTE: NOTE: NOTE: NOTE: NOTE: Results of article 2.2,2.4 and 2.4 are valid only for complete flight, that is when proejctile lands at
same horizontal level from which it has been projected.
Vertical component of velocity is zero when particle moves horizontally, i.e., at the highest point of
trajectory.
Vertical component of velocity is positive when particle is moving up and vertical component of
velocity is negative when particle is coming down if vertical upwards direction is taken as positive.
Any direction upward or downward can be taken as positive and if downward direction is taken as
positive then vertical component of velocity coming down is positive.
2.6 GENERAL RESULT :
(i) For maximum range = 45
R
max
=
g
u
2
In this situation
H
max
=
2
R
max
(ii) We get the same range for two angle of projections and (90 ) but in both cases,
maximum heights attained by the particles are different.
RESONANCE Page # 42 Page # 42 Page # 42 Page # 42 Page # 42
TM
(iii) f R = H
i.e.
g
2 sin u
2
=
g 2
sin u
2 2
tan = 4
(iv) Range can also be expressed as
R =
g
2 sin u
2
=
g
cos u . sin u 2
=
g
u u 2
y x
(v) CHANGE IN MOMENTUM :
(a) Initial velocity
i
u
r
= u cos i
+ u sin
j
(b) Final velocity
f
u
r
= u cos i
u sin
j
Change in velocity for complete motion
u
r
=
i f
u u
r r
= 2u sin
j
(c) Change in momentum for complete motion
P
r
=
i f
P P
r r
= m (
i f
u u
r r
) = m(2u sin )
j
= 2mu sin
j
(d) Velocity at the highest point =
f
u
r
= u cos i
Change in momentum at highest point
m (
i f
u u
r r
) = m [u cos i
(u cos
i
+ u sin
j
) = mu sin
j
Ex.1 A body is projected with a speed of 30 ms
1
at an angle of 30 with the vertical. Find the maximum height,
time of flight and the horizontal range of the motion. [ Take g = 10 m/s
2
]
Sol. Here u = 30 ms
1
, Angle of projection, = 90 30 = 60
Maximum height, H =
g 2
sin u
2 2
=
10
60 sin 30
2 2
=
4
3
20
900
=
4
135
m
Time of flight, T =
g
sin u 2
=
10
60 sin 30 2
0
=
3 3
sec.
Ex.2 A stone is thrown with a velocity v at angle with horizontal. Find its speed when it makes an angle with
the horizontal.
Sol. Since horizontal component of velocity remains constant. Therefore,
v cos = u cos u =
cos
cos v
RESONANCE Page # 43 Page # 43 Page # 43 Page # 43 Page # 43
TM
Ex.3 A projectile is thrown in the upward direction making an angle of 60
0
with the horizontal with a speed of 147
m/s. Find the time after which its inclination with the horizontal is 45
0
?
Sol. u
x
= 147 cos60
0
=
2
147
u
y
= 147 sin60
0
=
2
3 147
v
y
= u
y
+ a
y
t =
2
3 147
gt
v
x
= u
x
=
2
147
When angle is 45
0
, tan 45
0
=
x
y
v
v
v
y
= v
x
2
3 147
gt =
2
147
) 1 3 (
2
147
= gt t =
) 1 3 (
10 2
147
s
Ex.4 A large number of bullets are fired in all directions with the same speed v. What is the maximum area on the
ground on which these bullets will spread ?
Sol. Maximum distance upto which a bullet can be fired is its maximum range, therefore
R
max
=
g
v
2
Maximum area = (R
max
)
2
=
2
4
g
v
.
Ex.5 The velocity of projection of a projectile is given by : j
10 i
5 u + =
r
. Find
(a) Time of flight, (b) Maximum height, (c) Range
Sol. We have u
x
= 5 u
y
= 10
(a) Time of flight =
g
sin u 2
=
g
u 2
y
=
10
10 2
= 2 s
(b) Maximum height =
g 2
sin u
2 2
=
g 2
u
2
y
=
10 2
10 10
= 5 m
(c) Range =
g
cos u . sin u 2
=
10
5 10 2
= 10 m
HEIGHT AND RANGE :
Ex.6 A batter hits a baseball so that it leaves the bat with an initial speed v
0
= 37.0 m/s at an initial angle
0
= 53, at a location where g = 10.0 m/s
2
RESONANCE Page # 44 Page # 44 Page # 44 Page # 44 Page # 44
TM
(a) Find the position of the ball, and the magnitude and direction of its velocity, when t = 2.0 s.
(b) Find the time when the ball, reaches the highest point of flight and the find its height h at this point
(c) Find the horizontal range R - that is, the horizontal distance from the starting point to the point at
which the ball hits the ground.
For each part, treat the baseball as a projectile
Sol. The initial velocity of the ball has components
v
0x
= v
0
cos
0
= (37.0 m/s) cos 53 = 22.3 m/s
v
0y
= v
0
sin
0
= (37.0 m/s) sin 53 = 29.5 m/s
x= 46 m
t = 2.00 s
v
t = 3 s
1
v
1
y = 40 m h = 45 m
v = 37.0 m/s
0
0
= 53
t = 6 s
R = 138 m
v
2
x
y
(a) x = v
0x
t = (22.3 m/s) (2.00 s) = 44.6 m
y = v
0y
t
2
1
gt
2
= (29.5 m/s) (2 s)
2
1
(10 m/s
2
) (2 s)
2
= 59.0 20 = 39.0 m
v
x
= v
0x
= 22.3 m/s
v
y
= v
0y
gt = 29.5 m/s (10 m/s
2
) (2.00 s)
= 9.5 m/s
The y-component of velocity is positive, which means that the ball is still moving upward at this time (Figure).
The magnitude and direction of the velocity are
v =
2
y
2
x
v v + =
2 2
) s / m 5 . 9 ( ) s / m 3 . 22 ( +
= 24.2 m/s
= tan
1
s / m 3 . 22
s / m 0 . 10
= tan
1
0.4
(b) At the highest point, the vertical velocity v
y
is zero at time t
1
; then
v
y
= 0 = v
0y
gt
1
t
1
=
g
v
y 0
=
2
m/s 10
m/s 5 . 29
= 3.0 s
The height h at this time is the value of y when t = t
1
= 3 s;
h = v
0y
t
1
2
1
gt
1
2
= (29.5 m/s) (3.0 s)
2
1
(10.0 m/s
2
) (3.0 s)
2
= 88.5 45 = 43.5 m
(c) y = 0 = v
0y
t
2
=
2
1
gt
2
2
= t
2
2 y 0
gt
2
1
v
This is a quadratic equation for t
2
. It has two roots,
t
2
= 0 and t
2
=
g
v 2
y 0
= 2
s / m 10
) s / m 5 . 29 ( 2
= 5.9 s
There are two times at which y = 0; t
2
= 0 is the time the ball leaves the ground, and t
2
= 6 s is the time of its
return. This is exactly twice the time to reach the highest point, so the time of descent equals the time of
RESONANCE Page # 45 Page # 45 Page # 45 Page # 45 Page # 45
TM
ascent. (This is always true if the starting and end points are at the same elevation and air resistance can be
neglected).
The horizontal range R is the value of x when the ball returns to the ground, that is, at t = 6.64 s;
R = v
0x
t
2
= (22.3 m/s) (5.9 s) = 131.6 m
The vertical component of velocity when the ball hits the ground is
v
y
= v
0y
gt
2
= 29.5 m/s (10 m/s
2
) (5.9 s) = 29.5 m
That is, v
y
has the same magnitude as the initial vertical velocity v
0y
but the opposite direction (down). Since
v
x
is constant, the angle = 53 )(below the horizontal) at the point is the negative of the initial angle
0
= 53.
Ex.7 A clever monkey escapes from the zoo. The zoo keeper finds him in a tree. After failing to entice the monkey
and shoots. The clever monkey lets go at the same instant the dart leaves the gun barrel, intending to land
on the ground and escape. Show that the dart always hits the monkey, regardless of the darts muzzle
velocity (provided that it gets to the monkey before he hits the ground).
Sol. The monkey drops straight down, so x
monkey
= d at all times. For the dart, x
dart
= (v
0
cos a
0
)t. When these x-
coordinates are equal, d = (v
0
cos
0
)t, or
0 0
cos v
d
t
=
To have the dart hit the monkey, it must be true that y
monkey
= y
dart
at this same time. The monkey is in one-
dimensional free fall y
monkey
= d tan
0
2
1
gt
2
.
For the dart y
dart
= (v
0
sin
0
) t
2
1
gt
2
So if d tan
0
= (v
0
sin
0
) t at the time when the two x-coordinates are equal, then y
monkey
= y
dart
and we have
a hit.
Ex.8 A ball is thrwon from ground level so as to just clear a wall 4 m high at a distance of 4 m and falls at a distance
of 14 m from the wall. Find the magnitude and direction of the ball.
Sol. The ball passes through the point P(4, 4). So its range = 4 + 14 = 18 m.
The trajectory of the the ball is,
y = x tan ( 1
R
x
)
Now x = 4m, y = 4m and R = 18 m
4 = 4 tan
18
4
1
= 4 tan .
9
7
RESONANCE Page # 46 Page # 46 Page # 46 Page # 46 Page # 46
TM
or tan =
7
9
= tan
1
7
9
And R =
g
cos sin u 2
2
or 18 =
8 . 9
2
u
2
130
9
130
7
or u
2
=
7 9 2
130 8 . 9 18
= 182
or u =
182
and = tan
1
7
9
.
Qus. Two projectiles are thrown with different speeds and at different angles so as the cover the same maximum
height. Find out the sum of the times taken by each to the reach to highest point, if time of flight is T.
Ans. Total time taken by either of the projectile.
Qus. A particle is projected with speed 10 m/s at an angle 60
0
with horizontal. Find :
(a) time of flight (b) range
(c) maximum height (d) velocity of particle after one second.
(e) velocity when height of the particle is 1 m
Ans. (a)
3
sec. (b)
3 5
m (c)
4
15
m (d) 5.17 m/s
(e) j
55 i
5 v =
r
3. 3. 3. 3. 3. PR PR PR PR PROJECTILE THR OJECTILE THR OJECTILE THR OJECTILE THR OJECTILE THRO OO OOWN PARALLEL T WN PARALLEL T WN PARALLEL T WN PARALLEL T WN PARALLEL TO THE HORIZONT O THE HORIZONT O THE HORIZONT O THE HORIZONT O THE HORIZONTAL : AL : AL : AL : AL :
Consider a projectile thrown from point O at some height h from the ground with a velocity u. Now we shall
deal the characteristics of projectile motion with the help of horizontal and vertical direction motions.
Horizontal direction Vertical direction
(i) Initial velocity u
x
= u Initial velocity u
y
= 0
(ii) Acceleration a
x
= 0 Acceleration a
y
= g (downward)
3.1 TRAJECTORY EQUATION : The path traced by projectile is called the trajectory.
After time t,
x = ut ....(1)
y =
2
1
gt
2
....(2)
From equation (1) t = x/u
Put value of t in equation (2)
RESONANCE Page # 47 Page # 47 Page # 47 Page # 47 Page # 47
TM
y =
2
1
g .
2
2
u
x
This is trajectory equation of the projectile.
3.2 Velocity at a general point P(x, y)
v =
2
y
2
x
u u +
Here horizontal velocity of the projectile after time t
v
x
= u
velocity of projectile in vertical direction after time t
v
y
= 0 + (g)t = gt = gt (downward)
v =
2 2 2
t g u + and tan = v
y
/v
x
3.3 DISPLACEMENT : The displacement of the particle is expressed by
S = x
i
+ y j
= (ut)
i
+ (
2
1
gt
2
) j
where |S| =
2 2
y x +
3.4 TIME OF FLIGHT : This is equal to the time taken by the projectile to return to ground. From
equation of motion
S = ut +
2
1
at
2
Therefore for vertical direction h = v
y
t +
2
1
(g)t
2
At highest point v
y
= 0 h =
2
1
gt
2
t =
g
h 2
t =
g
h 2
3.5 HORIZONTAL RANGE : Distance covered by the projectile along the horizontal direction between
the point of projection to the point on the ground.
R = u
x
. t
R = u
g
h 2
RESONANCE Page # 48 Page # 48 Page # 48 Page # 48 Page # 48
TM
3.6 VELOCITY AT VERTICAL DEPTH h :
Along vertical direction v
y
2
= 0
2
+ 2 . (h) (g)
v
y
= gh 2
EXAMPLES BASED ON PROJECTILE PROJECTED HORIZONTALLY
Ex.9 A projectile is fired horizontally with a speed of 98 ms
1
from the top of a hill 490 m high. Find (i) the time
taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the
projectile hits the ground. (take g = 9.8 m/s
2
)
Sol. (i) The projectile is fired from the top O of a hill with speed u = 98 ms
1
along the horizontal as shown as OX.
It reaches the target P at vertical depth OA, in the coordinate system as shown, OA = y = 490 m
As, y =
2
1
gt
2
490 =
2
1
9.8 t
2
or t =
100
= 10 s.
(ii) Distance of the target from the hill is given by,
AP = x = Horizontal velocity time = 98 10 = 980 m.
(iii) The horizontal and vertical components of velocity v of the projectile at point P are
v
x
= u = 98 ms
1
v
y
= u
y
+ gt = 0 + 9.8 10 = 98 ms
1
V =
2
y
2
x
v v + =
2 2
98 98 + = 98
2
= 139 ms
1
Now if the resultant velocity v makes air angle with the horizontal, then
tan =
u
y
v
v
=
98
98
= 1 = 45
Ex.10 A motorcycle stunt rider rides off the edge of a cliff. Just at the edge his velocity is horizontal, with magnitude
9.0 m/s. Find the motorcycles position, distance from the edge of the cliff and velocity after 0.5 s.
Sol.
RESONANCE Page # 49 Page # 49 Page # 49 Page # 49 Page # 49
TM
At t = 0.50 s, the x and y-coordinates are
x = v
0x
t = (9.0 m/s) (0.50 s) = 4.5 m
y =
2
1
gt
2
=
2
1
(10 m/s
2
) (0.50 s)
2
= 1.2 m
The negative value of y shows that a this time the motorcycle is below its starting point.
The motorcycles distance from the origin at this time
r =
2 2
y x + =
2 2
) m 2 . 1 ( ) m 5 . 4 ( + =
2 2
m
10
12
m
10
45
=
2 2
) 4 ( ) 15 (
10
3
+
~
5 sec.
The components of velocity at this time are
v
x
= v
0x
= 9.0 m/s
v
y
= gt = (10 m/s
2
) (0.50 s) = 5 m/s.
The speed (magnitude of the velocity) at this time is
v =
2
y
2
x
v v + =
2 2
) s / m 5 ( ) s / m 0 . 9 ( + = 10.2 m/s
The angle of the velocity vector is
= tan
1
x
y
v
v
= tan
1
s / m 0 . 9
s / m 5
Qus. Two tall buildings face each other and are at a distance of 180 m from each other. With what velocity must a
ball be thrown horizontally from a window 55 m above the ground in one building, so that it enters a window
10.9 m above the ground in the second building.
Ans. 60 m/s.
Qus. Two paper screens A and B are separated by a distance of 100 m. A bullet pierces A and then B. The hole in
B is 10 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting the screen A,
calculate the velocity of the bullet when it hits the screen A. Neglect the resistance of paper and air.
Ans. 700 m/s
4. 4. 4. 4. 4. PROJECTILE FROM A TOWER PROJECTILE FROM A TOWER PROJECTILE FROM A TOWER PROJECTILE FROM A TOWER PROJECTILE FROM A TOWER
Case (i) : Horizontal projection
u
x
= u ; u
y
= 0 ; a
y
= g
Case (ii) : Projection at an angle above horizontal
u
x
= ucos ; u
y
= usin; a
y
= g
Case (iii) : Projection at an angle below horizontal
u
x
= ucos; u
y
= usin; a
y
= g
In all the above three cases, we can calculate the velocity of projectile at the instant of striking the ground by
using v =
2
y
2
x
v v + and tan =
x
y
v
v
, where is the angle at which the projectile strikes the ground.
RESONANCE Page # 50 Page # 50 Page # 50 Page # 50 Page # 50
TM
Ex.11 From the top of a 50m high tower a stone is projected with speed 10 m/s, at an angle of 37 as shown in
figure. Find out (a) velocity after 3s (b) time of flight. (c) horizontal range. (d) the maximum height attained by
the particle.
Sol. (a) Initial velocity in horizontal direction = 10 cos 37 = 8 m/s
Initial velocity in vertical direction = 10 sin 37 = 6 m/s
Velocity after 3 seconds
v = v
x
i
+ v
y
j
= 8
i
+ (u
y
+ a
y
t) j
= 8
i
24 j
(b) S
y
= u
y
t +
2
1
a
y
t
2
50 = 6 t +
2
1
(10) t
2
5t
2
6t 50 = 0 t =
10
1036 6
(c) Range = 8 (
10
1036 6
)
(d) v
y
= u
y
+ a
y
t
0 = 6 10t
t = 0.6
or 0 = 6 2 10 h
h = 1.8
maximum height = 50 + 1.8 = 51.8 m.
Qus. Two stones A and B are projected simultaneously from the top of a 100 m high tower. Stone B is projected
horizontally with speed 10 m/s, and stone A is dropped from the tower. Find out the following
(a) time of flight of the two stone.
(b) distance between two stones after 3 sec.
(c) angle of strike with ground.
(d) horizontal range of particle B.
Ans. (a)
5 2
sec. (b) x
B
= 30 m, y
B
= 45 (c)
5 2 tan
1
(d)
5 20
m
5. 5. 5. 5. 5. PR PR PR PR PROJECTION FR OJECTION FR OJECTION FR OJECTION FR OJECTION FROM A MO OM A MO OM A MO OM A MO OM A MOVING BOD VING BOD VING BOD VING BOD VING BODY YY YY
Consider a boy standing on a trolley who throws a ball with speed u at an angle with the horizontal. Trolley
moves horizontally with constant speed v .
Case (i) :
When ball is projected in the direction of motion of the trolley, horizontal component of balls velocity = u cos
+ v Initial vertical component of balls velocity = u sin
Case (ii) : The ball is projected opposite to the direction of motion of the trolley
Horizontal component of balls velocity = u cos v
Initial vertical component of balls velocity = u sin
RESONANCE Page # 51 Page # 51 Page # 51 Page # 51 Page # 51
TM
Case (iii) : The ball projected upwards from a platform moving with speed v upwards.
Horizontal component of balls velocity = u cos
Initial vertical component of balls velocity = u sin + v
Case (iv) : The ball projected upwards from a platform moving with speed v downwards.
Horizontal component of balls velocity = u cos
Initial vertical component of balls velocity = u sin v
Ex.12 A particle is projected at an angle of 30
0
with speed 20 m/s :
(i) Find out position vector of the particle after 1s
(ii) Find out angle betwen velocity vector and position vector at t = 1s
Sol. (i) s
x
= u cos t
= 20
2
3
t = 10
3
m
s
y
= u sin t +
2
1
10 t
2
= 20
2
1
1 5 (1)
2
= 5m
Position vector =
j
5 i
3 10 +
(ii) v
x
= 10
3
i
v
y
= u
y
+ a
y
t = 10 10 = 0
v
r
= 10
3
i
v
r
. s
r
= |v| |s| cos
cos =
325 3 10
3 10 3 10
=
325
3 10
=
13
3
2
=
13
3
2 cos
1
Ex.13 A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road
with an acceleration of 1 m/s
2
and the projection speed in the vertical direction is 9.8 m/s. How far behind the
boy will the ball fall on the car ?
Sol. Let the initial velocity of car be u. t =
g
u 2
= 2
where
u = component of velocity in vertical direction
x
c
= u 2 +
2
1
1 2
2
= 2u + 2
where x
c
= distance travelled by car
x
b
= distance travelled by ball
x
b
= 2u
x
c
x
b
= 2u + 2 2u
= 2m Ans.
RESONANCE Page # 52 Page # 52 Page # 52 Page # 52 Page # 52
TM
Qus. A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man
throws a ball in such a way that it returns to the truck after the truck has moved 58.8m. Find the speed and
the angle of projection (a) as seen from the truck , (b) as seen from the road.
[Ans : (a) 19.6 m/s upward (b) 24.5 m/s at 53 with horizontal]
6. 6. 6. 6. 6. PROJECTION ON AN INCLINED PLANE PROJECTION ON AN INCLINED PLANE PROJECTION ON AN INCLINED PLANE PROJECTION ON AN INCLINED PLANE PROJECTION ON AN INCLINED PLANE
To solve the problem of projectile motion on an incline plane we can adopt two types of axis system as
shown in the figures
Case (i) :
Up the incline
axis system 1 axis system 2
Here is angle of projection Here is angle of projection
with the horizontal. with the inclined plane
In this case: In this case:
a
x
= 0 u
x
= ucos a
x
= - gsin u
x
= ucos
a
y
= g u
y
= usin a
y
= - gcos u
y
= usin
Time of flight (T) :
when the particle strikes the inclined plane y coordinate
becomes zero
y = u
y
t +
2
1
a
y
t
2
0 = usinT
2
1
gcosT
2
T =
cos g
sin u 2
=
g
u 2
Maximum height (H) :
when half of the time is elasped y coordinate is equal to
maximum height of the projectile
H = u sin
cos g
sin u
2
cos g
sin u
sin g
2
1
H =
cos g 2
sin u
2 2
=
g 2
u
2
Range along the inclined plane (R):
When the particle strikes the inclined plane x coordinate
is equal to range of the particle
x = u
x
t +
2
1
a
x
t
2
R = ucos
cos g
sin u 2
2
cos g
sin u 2
cos g
2
1
R =
+
2
2
cos g
) cos( sin u 2
RESONANCE Page # 53 Page # 53 Page # 53 Page # 53 Page # 53
TM
Case (ii) :
Down the incline
axis system 1 axis system 2
In this case : In this case :
a
x
= 0 u
x
= ucos a
x
= gsin u
x
= ucos
a
y
= g u
y
= usin a
y
= gcos u
y
= usin
Time of flight (T) :
when the particle strikes the inclined plane y coordinate
becomes zero
y = u
y
t +
2
1
a
y
t
2
0 = usinT
2
1
gcosT
2
T =
cos g
sin u 2
=
g
u 2
Maximum height (H) :
when half of the time is elasped y coordinate is equal to
maximum height of the projectile
H = u sin
cos g
sin u
2
cos g
sin u
sin g
2
1
H =
cos g 2
sin u
2 2
=
g 2
u
2
Range along the inclined plane (R):
When the particle strikes the inclined plane x coordinate
is equal to range of the particle
x = u
x
t +
2
1
a
x
t
2
R = ucos
cos g
sin u 2
+
2
cos g
sin u 2
cos g
2
1
R =
2
2
cos g
) cos( sin u 2
RESONANCE Page # 54 Page # 54 Page # 54 Page # 54 Page # 54
TM
Table 1 : Standard results for projectile motion on an inclined plane
Up the Incline Down the Incline
Range
+
2
2
cos g
) cos( sin u 2
2
2
cos g
) cos( sin u 2
Time of flight
cos g
sin u 2
cos g
sin u 2
Angle of projection for
maximum range
2 4
2 4
Maximum Range
) sin 1 ( g
u
2
+
) sin 1 ( g
u
2
Here is the angle of projection with the incline and is the angle of incline.
NOTE: For a given speed, the direction - which gives the maximum range of the projectile on an incline, bisects the
angle between the incline and the vertical, for upward or downward projection.
Ex.14 A particle is projected horizontally with a speed u from the top of a plane inclined at an angle
with the
horizontal. How far from the point of projection will the particle strike the plane?
Sol. Take X,Y-axes as shown in figure. Suppose that the particle strikes the plane at a point P with coordinates
(x,y) . Consider the motion between A and P.
Motion in x direction :
Initial velocity = u
Acceleration = 0
x = ut......................(i)
Motion in y direction :
Initial velocity = u
Acceleration = g
y =
2
1
gt
2
.......................(ii)
Eliminating t from (i) and (ii)
y =
2
1
g
2
2
u
x
Also y = xtan
Thus ,
2
2
gu
gx
= xtan giving x = 0 or,
g
u 2
2
tan
Clearly the point P corresponds to x =
g
u 2
2
tan
then y = xtan =
g
u 2
2 2
tan
The distance AP =
2 2
y x +
RESONANCE Page # 55 Page # 55 Page # 55 Page # 55 Page # 55
TM
=
g
u 2
2
tan +
2
1 tan =
g
u 2
2
tan sec
Ex.15 A projectile is thrown at an angle with an inclined plane of inclination as shown in figure. Find the relation
between and if :
(a) projectile strikes the inclined plane perpendicularly,
(b) projectile strikes the inclined plane horizontal.
Sol. (a) If projectile strikes perpendicularly.
v
x
= 0 when projectile strikes
v
x
= u
x
+ a
x
t
0 = u cos g sin T
T =
sin g
cos u
we also know that T =
cos g
sin u 2
sin g
cos u
=
cos g
sin u 2
2 tan = cot
(b) If projectile strikes horizontally, then at the time of striking the projectile will be at the maximum
height from the ground. Therefore :
t
0P
=
cos g
sin u 2
t
0P
=
g 2
) sin( u 2
cos g
sin u 2
=
g 2
) sin( u 2 +
2 sin = sin ( + ) cos .
Elastic collision of a projectile with a wall :
Suppose a projectile is projected with speed u at an angle from point O on the ground. Range of the
projectile is R. If a wall is present in the path of the projectile at a distance x from the point O. The collision
with the wall is elastic, path of the projectile changes after the collision as described below.
Case I : If x
2
R
Direction of x component of velocity is reversed but its magnitude
remains the same and y component of velocity remains un-
changed, therefore the remaining distance (R x) is covered in
the backward direction and projectile falls a distance (R 2x)
ahead of the point O as shown in figure.
Case II : If x <
2
R
Direction of x component of velocity is reversed but its magnitude remains the same and y component of
velocity remains unchanged, therefore the remaining distance (R x) is covered in the backward direction
and projectile falls a distance (R 2x) behind the the point O as shown in figure.
RESONANCE
Page # 56 Page # 56 Page # 56 Page # 56 Page # 56
TM
Exercise 1
OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS
1. Two stones are projected from the same point with same speed making angles 45 + and 45 with the
horizontal respectively. If < 45, then the horizontal ranges of the two stones are in the ratio of
(A) 1 : 1 (B) 1 : 2 (C) 1 : 3 (D) 1 : 4
2. A hunter takes an aim at a monkey sitting an a tree and fires a bullet. Just when the bullet leaves barrel of the
gun, it so happens that the monkey begins to fall freely. The bullet will
(A) go above the monkey (B) go below the monkey
(C) hit the monkey
(D) may or may not hit the monkey. It will depend upon the velocity of the bullet.
3. It was calculated that a shell when fired form a gun with a certain velocity and at an angle of elevation
36
5
rad
should strike a given target. In actual practice, it was found that a hill just prevented the trajectory. At what
angle of elevation should the gun be fired to hit the target.
(A)
36
5
rad (B)
36
11
rad (C)
36
7
rad (D)
36
13
rad.
4. A projectile is thrown with a speed v at an angle with the vertical. Its average velocity between the instants
it crosses half the maximum height is
(A) v sin , horizontal and in the plane of projection
(B) v cos , horizontal and in the plane of projection
(C) 2v sin , horizontal and perpendicular to the plane of projection
(D) 2v cos , vertical and in the plane of projection.
5. Two bullets are fired horizontally, simultaneously and with different velocities from the same place. Which
bullet will hit the ground earlier?
(A) It would depend upon the weights of the bullets (B) The slower one.
(C) The faster one (D) Both will reach simultaneously.
6. A stone is thrown upwards. It returns to ground describing a parabolic path. Which of the following remains
constant?
(A) speed of the ball (B) kinetic energy of the ball
(C) vertical component of velocity (D) horizontal component of velocity.
7. A body is thrown horizontally with a velocity gh 2 from the top of a tower of height h. It strikes the level
ground through the foot of the tower at a distance x from the tower. The value of x is
(A) h (B)
2
h
(C) 2h (D)
3
h 2
8. A particle, with an initial velocity v
0
in a plane, is subjected to a constant acceleration in the same plane.
Then, in general, the path of the particle could be
(A) a circle (B) a straight line (C) a parabola (D) a hyperbola.
9. A ball is projected from a certain point on the surface of a planet at a certain angle with the horizontal surface.
The horizontal and vertical displacement x and y vary with time t in second as:
x = 10
t 3
and y = 10t t
2
The maximum height attained by the ball is
(A) 100 m (B) 75 m (C) 50 m (D) 25 m.
10. A bag is dropped from an aeroplane flying horizontally at a constant speed. If air resistance is ignored, where
will the aeroplane be when the bag hits the ground?
(A) ahead of the bag (B) directly above the bag
(C) far behind the bag (D) data is not sufficient.
RESONANCE
Page # 57 Page # 57 Page # 57 Page # 57 Page # 57
TM
11. The path of one projectile in motion as seen from another moving projectile is
(A) a straight line (B) a circle (C) an ellipse (D) a parabola.
12. A plane surface is inclined making an angle with the horizontal. From the bottom of this inclined plane, a
bullet is fired with velocity v. The maximum possible range of the bullet on the inclined plane is
(A)
g
v
2
(B)
) sin 1 ( g
v
2
+
(C)
) sin 1 ( g
v
2
(D)
) cos 1 ( g
v
2
+
13. A ball is projected horizontal with a speed v from the top of a plane inclined at an angle 45 with the
horizontal. How far from the point of projection with the ball strike the plane?
(A)
g
v
2
(B)
2
g
v
2
(C)
g
v 2
2
(D)
2
g
v 2
2
14. The time of flight of a projectile on an upward inclined plane depends upon
(A) angle of inclination of the plane (B) angle of projection
(C) the value of acceleration due to gravity (D) all of these.
15. A ball rolls of the top of a stairway horizontally with a velocity of 4.5 m s
1
. Each step is 0.2 m high and 0.3
m wide. If g is 10 ms
1
, then the ball will strike the nth step where n is equal to
(A) 9 (B) 10 (C) 11 (D) 12
16. The velocity of projection of a projectile is (6
i
+ 8 j
) ms
1.
. The horizontal range of the projectile is
(A) 4.9 m (B) 9.6 m (C) 19.6 m (D) 14 m.
17. If R and h represent the horizontal range and maximum height respectively of an obliquie projectile, then
h 8
R
2
+ 2h represents
(A) maximum horizontal range (B) maximum vertical range
(C) time of flight (D) velocity of projectile at highest point
18. A particle move along the parabolic path x = y
2
+ 2y + 2 in such a way that the y-component of velocity
vector remain 5m/s during the motion. The magnitude of the accleration of the particle is :
(A) 50 m/s
2
(B) 100 m/s
2
(C) 10
2
m/s
2
(D) 0.1 m/s
2
19. A ball is projected from point A with a velocity 10 m/s perpendicular to the inclined plane as shown in
figure. Range of the ball on the inclined plane is :
(A)
3
40
m (B)
13
20
m
(C)
20
13
m (D)
40
13
m
SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS
20. In order to project a body for maximum range, what is the condition ?
21. What is the angle between the directions of velocity & acceleraiton at the highest point of a projectile path ?
22. At what point of the projectile path the speed is minimum ?
23. Two bodies are projected at angles and (90 ) to the horizontal with the same speed. Find the ratio of their
times of flight?
24. In above question find the ratio of the maximum vertical heights ?
25. What should be the angles of projection to obtain maximum height and maximum time of flight ?
RESONANCE
Page # 58 Page # 58 Page # 58 Page # 58 Page # 58
TM
26. A bob of mass 0.1 kg hung from the ceiling of a room by a string 2 m long is set into oscillation. The speed
of the bob at its mean position is 1 ms
1
. What is the trajectory of the bob ; if the string is cut
(a) when the bob is at one of its extreme position
(b) at its mean position
27. A projectile can have the same range R for two angles of projections. If t
1
& t
2
be the times of flight in two
cases, then find out relation between t
1
t
2
and R ?
28. The height y and the distance x along the horizontal plane of a projectile on a certain planet (without no
surrounding atmosphere) are given by y = (8t 5t
2
) metere & x = 6t m. Then what will be the velocity of
projection ?
29. A glass marble projected horizontal from the top of a table falls at a distance x from the edge of the table. If
h is the height of the table, find the velocity of projection ?
30. A projectile is fired horizontally with a velocity of 98 m/s from the top of a hill 490 m high. Find :
(i) the time taken to reach the ground
(ii) the distance of the target from the hill
(iii) the velocity with which the particle hits the ground
31. The equation of a projectile is y =
3
x
2
gx
2
, find the angle of projection ?
32. Consider a boy on a trolley who throws a ball with speed 20 m/s at an angle 37
0
w.r.t. trolley which moves
horizontally with speed 10 m/s.
(a) Find horizontal and vertical components of initial velocity of ball when ball is projected in direction of
motion of trolley.
(b) Find horizontal and vertical components of initial velocity of ball when ball is projected opposite to direction
of motion of trolley
33. Consider a boy on a platform who throws a ball with speed 20 m/s at an angle 37
0
w.r.t. platform which moves
upwards with speed 10 m/s. (a) Find the horizontal and vertical component of balls velocity.
(b) Find horizontal and vertical components of balls velocity when ball is projected downwards from the
platform.
34. A bomb is dropped from an aeroplane moving horizontally at a certain height from the ground. Does the time
taken by the bomb to reach the ground depend on the velocity of the aeroplane ?
35. A particle is projected at an angle with an inclined plane making an angle with the horizontal as shown
in figure, speed of the particle is u, after time t find :
(a) x component of acceleration ?
(b) y component of acceleration ?
(c) x component of velocity ?
(d) y component of velocity ?
(e) x component of displacement ?
(f) y component of displacement ?
(g) y component of velocity when particle is at maximum distance from the incline plane ?
36. On an inclined plane of inclination 30, a ball is thrown at an angle of 60 with the horizontal from the foot of
the incline with a velocity of 10
3
ms
1
. If g = 10 ms
2
, then find the time in which ball will hit the inclined
plane?
37. The direction of motion of a projectile at a certain instant is inclined at an angle to the horizon. After
t seconds it is inclined an angle . Find the horizontal component of velocity of projection in terms of
g, t , and .
RESONANCE
Page # 59 Page # 59 Page # 59 Page # 59 Page # 59
TM
38. A radius vector of a point A relative to the origin varies with time t as
r
r
=
j
2
t b i
t a
, where a and b
are positive constants and j
and i
are the unit vectors of the x and y axes. Find:
(i) the equation of the point's trajectory y (x) ; plot this function
(ii) the time dependence of the velocity v and acceleration a vectors as well as of the
moduli of these quantities .
39. Two particles are projected simultaneously with the same speed V in the same vertical plane with
angles of elevation and 2
, where
< 45 . At what time will their velocities be parallel.
40. If 4 seconds be the time in which a projectile reaches a point P of its path and 5 seconds the time from
P till it reaches the horizontal plane through the point of projection . Find the height of P above the
horizontal plane. [ g = 9.8 m/sec
2
]
41. A man is travelling on a flat car which is moving up a plane inclined
at cos
= 4/5 to the horizontal with a speed 5 m/s. He throws a ball
towards a stationary hoop located perpendicular to the incline in such
a way that the ball moves parallel to the slope of the incline while going
through the centre of the hoop. The centre of the hoop is 4 m high from
the man's hand calculate the time taken by the ball to reach the hoop.
4
m
5
m
/
s
1. A ship is approaching a cliff of height 105 m above sea level. A gun fitted on the ship can fire shots with
a speed of 110 ms
1
. Find the maximum distance from the foot of the cliff from where the gun can hit an
object on the top of the cliff. [ g = 10 m/s
2
] [REE '94, 6]
2. Two towers AB and CD are situated a distance '
d
' apart as shown in
the fig. AB is 20 m high and CD is 30 m high from the ground. An object
of mass '
m
' is thrown from the top of AB horizontally with a velocity of
10 m/s towards CD. Simultaneously another object of mass 2
m is
thrown from the top of CD at an angle of 60 to the horizontal towards
AB with the same magnitude of initial velocity as that of the first object.
The two objects move in the same vertical plane, collide in mid air and
stick to each other.
(i) calculate the distance '
d
' between the towers.
(ii) find the position where the objects hit the ground. [JEE ' 94, 6]
3. A building 4.8 m high 2b meters wide has a flat roof. A ball is projected from a point on the horizontal
ground 14.4 m away from the building along its width. If projected with velocity 16 m/s at an angle
of 45 with the ground, the ball hits the roof in the middle, find the width 2b. Also find the angle of
projection so that the ball just crosses the roof if projected with velocity 10 3 m/s. [REE '95, 6]
4. Two guns situated on the top of a hill of height 10 m, each fired shots with the same speed 5 3 m/s
at some interval of time. One gun fires horizontally and other fires upwards at an angle of 60 with the
horizontal. The shot collide in air at a point P. Find: [JEE '96, 5]
(i) the time interval between the firings and
(ii) the coordinates of the point P.
Take origin of the coordinate system at the foot of the hill right below the muzzle and trajectories in x-
y plane.
5. A vertical pole has a red mark at some height. A stone is projected from a fixed point on the ground.
When projected at an angle of 45 it hits the pole orthogonally 1
m above the mark. When projected
with a different velocity at an angle of tan
1
(3/4), it hits the pole orthogonally 1.5
m below the mark. Find
the velocity and angle of projection so that it hits the mark orthogonally to the pole. [ g = 10 m/sec
2
]
[REE '96, 6 ]
RESONANCE
Page # 60 Page # 60 Page # 60 Page # 60 Page # 60
TM
6. The trajectory of a projectile in a vertical plane is y = ax
bx
2
, where a, b are constants and x and y are
respectively the horizontal and vertical distances of the projectile from the point of projection. The maximum
height attained is _______ and the angle of projection from the horizontal is _______. [JEE '97, 2]
7. The coordinates of a particle moving in a plane are given by x (t) = a cos (p
t) and
y (t) = b sin (p
t), where a, b (< a) and p are positive constants of appropriate dimensions.
(A) the path of the particle is an ellipse
(B) the velocity and acceleration of the particle are normal to each other at t = /2p
(C) the acceleration of the particle is always directed towards a focus
(D) the distance travelled by the particle in time interval t = 0 to = /2p is a. [JEE '99, 2]
8. An object A is kept fixed at the point
x = 3 m and
y = 1.25 m on a
plank P raised above the ground. At time t = 0 the plank starts moving
along the + x direction with an acceleration 1.5 m/s
2
. At the same
instant a stone is projected from the origin with a velocity u as shown.
A stationary person on the ground observes the stone hitting the object
during its downward motion at an angle of 45 to the horizontal. All the
motions are in x-y plane. Find u and the time after which the stone
hits the object. [ Take g = 10 m/s
2
] [JEE 2000, 5]
9. Shots fired simultaneously from the top and foot of a vertical cliff at elevations of 30
0
and 60
0
respectively,
strike an object simultaneously which is at a height of 100 meters from the ground and at a horizontal
distance of 200 3 meters from the cliff. Find the height of the cliff, the velocities of projection of the
shots and the time taken by the shots to hit the object. [ REE 2000, 5 ]
EXERCISE # 1 EXERCISE # 1 EXERCISE # 1 EXERCISE # 1 EXERCISE # 1
OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS OBJECTIVE PROBLEMS
1. A 2. C 3. D 4. A
5. D 6. D 7. C 8. B,C
9. D 10. B 11. A 12. B
13. D 14. D 15. A 16. B
17. A 18. A 19. A
SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS SUBJECTIVE PROBLEMS
20. Angle of projection = 45
0
. 21. 90
0
.
22. At the highest point. 23. sin : cos
24. sin
2
: cos
2
25. (a) = 90
0
, (b) = 90
0
.
26. (a) vertically downwards (b) parabolic path
27. t
1
t
2
= 2R/g 28. 10 m/s 29. x
h 2
g
30. (i) 10 sec. (ii) 980 m (iii) 138.59 m/s
31. tan =
3
32. (a) 26, 12 (b) 6, 12
33. (a) 16, 22 (b) 16, 2 34. No
35. (a) g sin, (b) g cos, (c) u cos g sin t, (d)
u sin gcos t, (e) u cos t
2
1
g sin t
2
, (f)
u sin t
2
1
g cos t
2
, (g) zero.
36. 2 s 37.
tan tan
gt
38. (i) y =
bx
a
2
2
(ii)
r
v =
a i bt j
$ $
2
,
r
= 2 b
$
j
,
r
v =
a b t
2 2 2
4 +
,
r
= 2
b
39.
2
3
ec cos
2
cos
g
v
40. 98 meters 41. 1 s
EXERCISE # 2 EXERCISE # 2 EXERCISE # 2 EXERCISE # 2 EXERCISE # 2
1. 1100 m
2. (i) 17.32 m
(ii) combined mass strikes at 11.55 m from B
and 5.77 m from D
3. width of the roof is 9.6 m; = tan
1
2
3
4. (i) 1 s (ii) ( 5 , 3 5 )
5.
3
3620
m/s , tan
1
10
9
6.
b 4
a
2
, tan
1
a
7. A, B 8. u = 7.29 m/s, t = 1 s.
9. 400 m, V
T
= 40
3
m/s, V
F
= 40 m/s, T = 10 s.
Das könnte Ihnen auch gefallen
- Chapter 3: KinematicsDokument70 SeitenChapter 3: KinematicsCk100% (1)
- Rectiliner Motion - Jee (Main+advanced)Dokument43 SeitenRectiliner Motion - Jee (Main+advanced)Resonance Dlpd86% (103)
- Kinematics Important Questions and Solutions For JEE Main and AdvancedDokument19 SeitenKinematics Important Questions and Solutions For JEE Main and AdvancedRavindra KumarNoch keine Bewertungen
- Disha Rare Kota Physics DPPDokument404 SeitenDisha Rare Kota Physics DPPRim MishraNoch keine Bewertungen
- JEE Advanced Assign - Physics PDFDokument26 SeitenJEE Advanced Assign - Physics PDFaumoghNoch keine Bewertungen
- Unit & Dimension PDFDokument22 SeitenUnit & Dimension PDFAnand Classes86% (7)
- IIT JEE Coordinate Geometry - Preparation Tips To Practical Applications! - askIITiansDokument19 SeitenIIT JEE Coordinate Geometry - Preparation Tips To Practical Applications! - askIITiansaskiitian67% (3)
- Iit Jee StudyDokument955 SeitenIit Jee StudyGarlapati Srinivasa Rao88% (17)
- Bansal CLasses Physics Study Material For IIT JEEDokument521 SeitenBansal CLasses Physics Study Material For IIT JEEmuno93% (14)
- Summay Chapter 6 and 8 (Paul Goodwin and George Wright)Dokument10 SeitenSummay Chapter 6 and 8 (Paul Goodwin and George Wright)Zulkifli SaidNoch keine Bewertungen
- Surface Chemistry DPP PDFDokument7 SeitenSurface Chemistry DPP PDFDevendra ShuklaNoch keine Bewertungen
- Physics ReviewerDokument21 SeitenPhysics ReviewerainnahNoch keine Bewertungen
- Aakash Physics Module 1Dokument247 SeitenAakash Physics Module 1ASHISH NAIK82% (11)
- Catalysers Physics - JEE AdvancedDokument220 SeitenCatalysers Physics - JEE AdvancedChaitanya Pandey100% (1)
- Gaussian Beam OpticsDokument16 SeitenGaussian Beam OpticsModyKing99Noch keine Bewertungen
- Aakash Physics Study Package 3 SolutionsDokument218 SeitenAakash Physics Study Package 3 Solutionsfociwe100% (1)
- Sep 02Dokument19 SeitenSep 02c_nghia100% (1)
- JEE Advanced Previous Year Questions, KinematicsDokument7 SeitenJEE Advanced Previous Year Questions, KinematicsAnil Kapil100% (4)
- KinematicsDokument9 SeitenKinematicsRekha PurohitNoch keine Bewertungen
- Fiitjee PhysicsDokument14 SeitenFiitjee PhysicsKrishna Priya100% (7)
- Bansal Modern PhysicsDokument27 SeitenBansal Modern Physicsbhnprtp90Noch keine Bewertungen
- DPP - ElectrostaticsDokument16 SeitenDPP - ElectrostaticsVineet GoyalNoch keine Bewertungen
- 111narayana PhysicsDokument41 Seiten111narayana Physicssanjay100% (2)
- Work, Energy and PowerDokument80 SeitenWork, Energy and PowerJack Lupino100% (1)
- Sterling - JEE - Physics - (Elasticity Thermal Exp, Calorimetry & Heat Transfer) - EngDokument51 SeitenSterling - JEE - Physics - (Elasticity Thermal Exp, Calorimetry & Heat Transfer) - EngRamJiPandeyNoch keine Bewertungen
- MSC - Patran Results PrimerDokument138 SeitenMSC - Patran Results PrimeralfredaoudeNoch keine Bewertungen
- DC Pandey Part 1Dokument244 SeitenDC Pandey Part 1Nishchal100% (1)
- Tiliner Motion - Jee Main AdvancedDokument69 SeitenTiliner Motion - Jee Main AdvancedAnubhav KohliNoch keine Bewertungen
- Narayana Physics ADV Material - 1Dokument32 SeitenNarayana Physics ADV Material - 1Sri VarshiniNoch keine Bewertungen
- Electrostatics NarayanaDokument66 SeitenElectrostatics NarayanaChandan18041970100% (1)
- AKAsh GravitationDokument36 SeitenAKAsh GravitationDaitya PurushNoch keine Bewertungen
- Electro QB BansalDokument20 SeitenElectro QB BansalAnshul TiwariNoch keine Bewertungen
- Resonance PhyDokument37 SeitenResonance PhyRavi57% (7)
- Master Stroke Assgnment PhysicsDokument381 SeitenMaster Stroke Assgnment Physicsobi-wan kenobiNoch keine Bewertungen
- IIT JEE - Rotation Motion (MAINS)Dokument6 SeitenIIT JEE - Rotation Motion (MAINS)yashsodhaniNoch keine Bewertungen
- Phy NeetDokument308 SeitenPhy NeetSona Jithin100% (1)
- Landing Gear Design and DevelopmentDokument12 SeitenLanding Gear Design and DevelopmentC V CHANDRASHEKARANoch keine Bewertungen
- Bansal Current ElectricityDokument27 SeitenBansal Current Electricitysudhanva mattupalli100% (1)
- IIT Class XI Phy Rotation MotionDokument70 SeitenIIT Class XI Phy Rotation MotionDivyanshu Verma100% (2)
- Aakash 01 - Electrostatics PDFDokument18 SeitenAakash 01 - Electrostatics PDFRishabh Agarwal100% (2)
- The Essentials of Machine Learning in Finance and AccountingDokument259 SeitenThe Essentials of Machine Learning in Finance and Accountingernestdark11100% (1)
- TIMO Selection Primary 5Dokument2 SeitenTIMO Selection Primary 5Qurniawan Agung Putra100% (5)
- Physics Vector By: Vidyamandir ClassesDokument29 SeitenPhysics Vector By: Vidyamandir ClassesKainshk Gupta50% (2)
- Iit Mains Exam Type Questions of Electrostatics PDFDokument13 SeitenIit Mains Exam Type Questions of Electrostatics PDFRupinder Sidhu100% (2)
- DPP Booklet (All Subject) @class - 10 - MaterialsDokument67 SeitenDPP Booklet (All Subject) @class - 10 - MaterialsShashwat MishraNoch keine Bewertungen
- Master Assignment PDFDokument88 SeitenMaster Assignment PDFTanishque SinghNoch keine Bewertungen
- Achiever'S Comprehensive Course (Faqs)Dokument9 SeitenAchiever'S Comprehensive Course (Faqs)microdotcdmNoch keine Bewertungen
- Circular Motion ResonanceDokument27 SeitenCircular Motion ResonanceSAMRIDHI100% (3)
- 11-Wave Optics - (Assignment)Dokument19 Seiten11-Wave Optics - (Assignment)ENGLISH MEDIUMNoch keine Bewertungen
- THERMODYNAMICS Complete Short Notes Physical Chemistry by AKK SirDokument14 SeitenTHERMODYNAMICS Complete Short Notes Physical Chemistry by AKK SirAkNoch keine Bewertungen
- Kinematics 1Dokument3 SeitenKinematics 1bishu_iitNoch keine Bewertungen
- Particle Dynamics - Mechanics For IIT JEEDokument34 SeitenParticle Dynamics - Mechanics For IIT JEEfaizan123khanNoch keine Bewertungen
- Bansal KinematicsDokument16 SeitenBansal KinematicsPranav DarganNoch keine Bewertungen
- Fiitjee Mains Paper (Two Year Crp1416)Dokument25 SeitenFiitjee Mains Paper (Two Year Crp1416)Kaushal Baid100% (1)
- Kinematics Theory - EDokument24 SeitenKinematics Theory - Ethinkiit100% (1)
- Lecture 1Dokument28 SeitenLecture 1ايلاف المنيعNoch keine Bewertungen
- Unit 1: MAT113: Elementary MechanicsDokument41 SeitenUnit 1: MAT113: Elementary MechanicsỌláOlúwakìítán AgboọláNoch keine Bewertungen
- General Physics (1) For Engineering: Textbook: Physics For Scientists and Engineers, Seventh Edition, Jewett / SerwayDokument54 SeitenGeneral Physics (1) For Engineering: Textbook: Physics For Scientists and Engineers, Seventh Edition, Jewett / SerwayZaidHomsiNoch keine Bewertungen
- Chapter 3 Kinematics Part 1Dokument37 SeitenChapter 3 Kinematics Part 1farahhananiNoch keine Bewertungen
- Lectur-1 12.2Dokument21 SeitenLectur-1 12.2FaIz FauziNoch keine Bewertungen
- B Motion in A Straight LineDokument24 SeitenB Motion in A Straight Linef20230069Noch keine Bewertungen
- Kinematics of ParticlesDokument14 SeitenKinematics of ParticlesIMADE MIRACLENoch keine Bewertungen
- Chapter 2 Motion in One Dimension - 2024 NotesDokument15 SeitenChapter 2 Motion in One Dimension - 2024 NoteseverlynkhwaweNoch keine Bewertungen
- PDF - Chapter 1 - Particle Kinematic - BMCG - FullDokument92 SeitenPDF - Chapter 1 - Particle Kinematic - BMCG - FullTakip MatNoch keine Bewertungen
- 3rd WeekDokument7 Seiten3rd WeekNanzkie Andrei SamanNoch keine Bewertungen
- Distance and Displacement:: What Is Velocity?Dokument8 SeitenDistance and Displacement:: What Is Velocity?Muhammad QasimNoch keine Bewertungen
- CH-9-Centre-of-Mass - PDF: Sign inDokument1 SeiteCH-9-Centre-of-Mass - PDF: Sign inrahuljain1Noch keine Bewertungen
- WEP Narayana SheetsDokument6 SeitenWEP Narayana Sheetsrahuljain1100% (1)
- WEP Narayana SheetsDokument6 SeitenWEP Narayana Sheetsrahuljain1100% (1)
- Leph 201Dokument42 SeitenLeph 201rahuljain1Noch keine Bewertungen
- Queen's University Belfast: Phy3012 Solid State PhysicsDokument131 SeitenQueen's University Belfast: Phy3012 Solid State PhysicsOğuz Alp KurucuNoch keine Bewertungen
- PTM Phy F.4.Ch.2.4Dokument13 SeitenPTM Phy F.4.Ch.2.4Bazil BoliaNoch keine Bewertungen
- WiproDokument44 SeitenWiproapi-26541915Noch keine Bewertungen
- Cost-Volume-Profit Relationships: © 2010 The Mcgraw-Hill Companies, IncDokument97 SeitenCost-Volume-Profit Relationships: © 2010 The Mcgraw-Hill Companies, IncInga ApseNoch keine Bewertungen
- One Sample Z TestDokument10 SeitenOne Sample Z TestCornelius DuraiNoch keine Bewertungen
- JEE Class Companion Physics: Module-2Dokument7 SeitenJEE Class Companion Physics: Module-2neoisonlyoneNoch keine Bewertungen
- NMDokument12 SeitenNMShravan KumarNoch keine Bewertungen
- Computer Programming Assignment - 3Dokument3 SeitenComputer Programming Assignment - 3Waqas MehmoodNoch keine Bewertungen
- Extraction and Leaching 93851 - 14 ADokument18 SeitenExtraction and Leaching 93851 - 14 Aakarcz6731Noch keine Bewertungen
- 0607 s10 QP 2Dokument12 Seiten0607 s10 QP 2Amalia KorakakiNoch keine Bewertungen
- Electricity, Magnetism and Modern PhysicsDokument12 SeitenElectricity, Magnetism and Modern Physicsxtor787898Noch keine Bewertungen
- Data Mining With Weka: Ian H. WittenDokument33 SeitenData Mining With Weka: Ian H. WittenQuân PhạmNoch keine Bewertungen
- Mean and Median.Dokument3 SeitenMean and Median.shailesh100% (1)
- Lesson 3 - Demand and SupplyDokument79 SeitenLesson 3 - Demand and SupplyRounak TiwariNoch keine Bewertungen
- PQ - With - Id - PDF fkj1 PDFDokument17 SeitenPQ - With - Id - PDF fkj1 PDFWorse To Worst SatittamajitraNoch keine Bewertungen
- MODULE 3 and 4Dokument6 SeitenMODULE 3 and 4Jellene Jem RonarioNoch keine Bewertungen
- 0216 GonzaDokument8 Seiten0216 GonzaSunil AundhekarNoch keine Bewertungen
- Digital SignatureDokument49 SeitenDigital SignatureVishal LodhiNoch keine Bewertungen
- Crystal Ball Report - FullDokument7 SeitenCrystal Ball Report - FullVan A HoangNoch keine Bewertungen
- Plaxis 3DDokument41 SeitenPlaxis 3DafvilavilanoriegaNoch keine Bewertungen
- Perimeter & Area: Section - ADokument5 SeitenPerimeter & Area: Section - AKrishna Agrawal100% (1)
- Chapter One Part 1Dokument20 SeitenChapter One Part 1enedaylalu bassieNoch keine Bewertungen
- Integrals of Differential Binomials and Chebyshev's CriterionDokument4 SeitenIntegrals of Differential Binomials and Chebyshev's CriterionEnrique GonzalezNoch keine Bewertungen