EE 250: Probability, Random

Variables and Stochastic Processes

MIDTERM 2
PRACTICE PROBLEM SOLUTIONS
SJSU
Fall 2012

EE250 - Midterm 2 Practice Problems

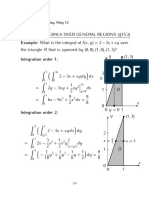
Problem 1. The random variables X and Y have the joint pdf

{
C if (x,y) belongs to the shaded region in Fig. 1
fX,Y (x, y) =
0
o.w.

000000
0000
1111
2 111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
1 111111
0
1
000000
111111
0
1
000000
111111
0
1
000000
111111
0
1
000000
111111
0
1
000000
111111
0
1
000000
111111
1

Figure 1: Sample space for (X, Y )

a) Find C such that fX,Y (x, y) is a valid pdf.
Solution:
The shaded area is 2; hence,
C = 1/2.
b) (10 points) Find the marginal pdf fX (x).
Solution: If 0 < x < 1, then
x+1
1
1
fX (x) =
dx = (x + 1).
2
2
0
If 1 < x < 2, then

fX (x) =
x1

1
1
dx = (2 x).
2
2

c) (10 points) Find the mean(or expectation) of the random variable g(Y ) =
E[X|Y ]. You can leave the answer as an integral. You dont need to
evaluate it.

EE250 - Midterm 2 Practice Problems

Solution:

1
x (x + 1)dx +
2

E[E[X|Y ]] = E[X] =
0

1
x (2 x)dx.
2

d) (10 points) Find the conditional pdf fY |X (y|x).

Solution:
f (x, y)
fY |X (y|x) =
.
fX (x)
If 0 < x < 1, then
fY |X (y|x) =

1/2
1
=
,
1/2(x + 1)
x+1

0 < y < x + 1.

If 1 < x < 2, then

fY |X (y|x) =

1
1/2
=
. x 1 < y < 1.
1/2(2 x)
2x

e) (10 points) Find E[Y |X = x].

Solution: If 0 < x < 1, then

x+1

E[Y |X = x] =

y
0

x+1
1
dx =
.
x+1
2

If 1 < x < 2, then

E[Y |X = x] =

y
x1

1
x
dx = .
2x
2

EE250 - Midterm 2 Practice Problems

Problem 2. Let both X and Y be uniformly distributed in the interval [1, 1].
Assume that X and Y are independent. Let
Z1 = XY, and Z2 = X + Y.
a) (13 points) Find P [Z1 z] when z > 0.
Solutions:
1
f (x, y) = , 1 < x < 1, 1 < y < 1.
4

1
xy = z

z
z
1

z
xy = z

y
Figure 2: Problem 2a)
Assuming 1 > z > 0, we should integrate the joint pdf over the shaded
region in the above figure in order to obtain the result.
1 1
1 1
1
1
dydx = + z z ln(z).
P [Z1 z] = 1 2
2 2
2
z
z/x 4

EE250 - Midterm 2 Practice Problems

b) (13 points) Find P [Z2 z] when z < 0.

1
z+1
z+1

z
1

z
1

x+y = z

Figure 3: Problem 2b)

Assuming 2 < z < 0, we should integrate the joint pdf over the shaded
region in the above figure in order to obtain the result.
z+1 zx
1
(z + 2)2
P [Z2 z] =
dydx =
.
4
8
1
1
c) (12 points) Calculate E[Z1 ] and V ar[Z1 ]. (Hint: You do not need to
calculate the pdf of Z1 .)
Solution: Note that X and Y are independent.
E[Z1 ] = E[XY ] = E[X]E[Y ] = 0.
1
E[Z12 ] = E[X 2 Y 2 ] = E[X 2 ]E[Y 2 ] = .
9
Then,
1
V ar[Z1 ] = E[Z12 ] (E[Z1 ])2 = .
9
d) (12 points) Calculate P [max(X, Y ) > 1/3|Z2 > 2/3].
Solution:

P [max(X, Y ) > 1/3|Z2 > 2/3] =

P [{max(X, Y ) > 1/3} {X + Y > 2/3}]

.
P [X + Y > 2/3]

EE250 - Midterm 2 Practice Problems

1
2/3
1/3

1/3
1

1/3

1/3 2/3 1

Shaded RegionI

Shaded RegionII

Figure 4: Problem 2d)

See the above figure. The shaded region-I corresponds to the event
{max(X, Y ) > 1/3} and the shaded region-II corresponds to the event
{X + Y > 2/3}. Observe that the event {max(X, Y ) > 1/3} {X + Y >
2/3} can also be represented by shaded region-II. Hence,
P [max(X, Y ) > 1/3|Z2 > 2/3] =

Area of Shaded Region-II

= 1.
Area of Shaded Region-II

EE250 - Midterm 2 Practice Problems

Problem 3. A fair coin is thrown. The random variables X and Y have the
conditional joint pdf
{
K1 (x + y) if 0 < x < 1, 0 < y < 1
fX,Y (x, y | Coin = T ail) =
0
o.w.
{
fX,Y (x, y | Coin = Head) =

K2 x if 0 < x < y < 1

0
o.w.

a) Find K1 , K2 such that fX,Y (x, y | Coin = head) and fX,Y (x, y | Coin =
tail) are a valid conditional pdfs.
Solution: Conditional pdfs should integrate to 1:
1 1
K1 (x + y)dxdy = 1 = K1 = 1.
0

K2 xdydx = 1 = K2 = 1/6.
0

b) Find the joint pdf fX,Y (x, y). Sketch the sample space.
Solution:
fX,Y (x, y) = fX,Y (x, y | Coin = Heads)P (Coin = Heads) +
fX,Y (x, y | Coin = T ails)P (Coin = T ails).
= fX,Y (x, y | Coin = Heads)0.5 + fX,Y (x, y | Coin = T ails)0.5.
{
(x + y)/2
0 < x < 1, 0 < y < x
=
(7x + y)/2 0 < x < 1, x < y < 1
y
f(x,y) = 7x/2+y/2
1
f(x,y) = x/2+y/2
1

Figure 5: Problem-1b

EE250 - Midterm 2 Practice Problems

b) Find the marginal pdf fX (x).

Solution:
For 0 < x < 1,

fX (x) =
f (x, y)dy
1
x
(7x + y)/2 dy
(x + y)/2 dy +
=

(1)
(2)

= 1/4 + 7x/2 3x2

(3)

c) Find the conditional pdf fY |X (y|x).

Solution:
fY |X (y, x) =
{
fY |X (y, x) =

fX,Y (x, y)
.
fX (x)

(x+y)/2
(1/4+7x/23x2 )
(7x+y)/2
(1/4+7x/23x2 )

0 < x < 1, 0 < y < x

0 < x < 1, x < y < 1

d) Find E[Y |X = x].

Solution:
x
1
E[Y |X = x] =
yf (y|x)dy +
yf (y|x)dy
0
x
1
x
(7x + y)/2
(x + y)/2
dy +
y
dy
=
y
2
(1/4 + 7x/2 3x )
(1/4 + 7x/2 3x2 )
x
0
3x2 7x 1
=
+
+
(4)
2
4
6

EE250 - Midterm 2 Practice Problems

Problem 4. Let X and Y denote jointly Gaussian random variables with

means E[X] = 1 and E[Y ] = 2 and variances V ar[X] = 1, V ar[Y ] = 9 and
covariance Cov(X, Y ) = 2. Let
Z1 = 2X + 3Y, and Z2 = aX Y.
Solution: Note that Z1 and Z2 are jointly Gaussian since they are written as
linear combinations of the jointly Gaussian random variables. Then, both Z1
and Z2 are Gaussian.
a) Find P [Z1 z].
Solution: Since Z1 is Gaussian, in order to find its pdf we only need
E[Z1 ] and V ar[Z1 ].
E[Z1 ] = E[2X + 3Y ] = 2E[X] + 3E[Y ] = 8.
E[Z12 ] = E[(2X + 3Y )2 ] = E[4X 2 + 9Y 2 + 12XY ].
We know that E[X 2 ] = V ar[X] + (E[X])2 = 1 + 12 = 2, and E[Y 2 ] =
V ar[Y ] + (E[Y ])2 = 9 + 22 = 13. Using the covariance matrix of (X, Y ),
we obtain
E[XY ] E[X]E[Y ] = 2 = E[XY ] = 2 + 2 = 4.
Then,
V ar[Z1 ] = E[Z12 ] (E[Z1 ])2 = 4 2 + 9 13 + 12 4 82 = 109.
(
P [Z1 z] = 1 [Z1 > z] = 1 Q

z E[Z1 ]

V ar[Z1 ]

(
=1Q

z8

109

)
.

b) Calculate E[Z2 ] and E[Z1 Z2 ] in terms of a. (Hint: You do not need to

calculate pdfs of Z1 and Z2 .)
Solution:
E[Z2 ] = E[aX Y ] = aE[X] E[Y ] = a 2.

E[Z1 Z2 ] = E[(2X + 3Y )(aX Y )]

= 2aE[X 2 ] 2E[XY ] + 3aE[XY ] 3E[Y 2 ]
= = 16a 47

EE250 - Midterm 2 Practice Problems

10

c) Calculate P [min(X, Y ) > 1/3|Z1 > 1/3].

Solution:
P [min(X, Y ) > 1/3, Z1 > 1/3]
P [Z1 > 1/3]
P [min(X, Y ) > 1/3]
=
P [Z1 > 1/3]
P [X > 1/3, Y > 1/3]
=
P [Z1 > 1/3]

P [min(X, Y ) > 1/3 | Z1 > 1/3] =

P [X > 1/3, Y > 1/3] =

f (x, y)dxdy
1/3

1/3

1/3

1/3

e0.5[X
2 |KX,Y |

1
Y ]KX,Y
[X

Y ]T

dxdy,

where [X Y ]T denotes the transpose of the row vector [X Y ].

Using part-a,
(
)
(
)
23/3
1/3 E[Z1 ]
P [Z1 > 1/3] = Q
=Q
.
109
V ar[Z1 ]
Then,

P [min(X, Y ) > 1/3 | Z1 > 1/3] =

1/3

1/3 2

e0.5[X Y ]KX,Y [X
(
)
23/3

Q
109

|KX,Y |

Y ]T

dxdy
.

EE250 - Midterm 2 Practice Problems

11

1111111111111111
0000000000000000
0000000000000000
1111111111111111
00000000000
11111111111
0000000000000000
1111111111111111
00000000000
11111111111
0000000000000000
1111111111111111
00000000000
11111111111
0000000000000000
1111111111111111
00000000000
11111111111
0000000000000000
1111111111111111
00000000000
11111111111
0000000000000000
1111111111111111
00000000000
11111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
mi

n(x

1/3

1/3
x
2x

111111
000000
000000
111111
000000
111111
000000
111111
2x

+3

y=

1/3

Figure 6: Problem-2c

+3

y>

1/3

,y)

>1

/3

EE250 - Midterm 2 Practice Problems

12

d) Find a such that Z1 , Z2 are independent. What can you say about the
joint distribution of Z1 , Z2 for a given a?
Solution: If two Gaussian random variables are uncorrelated, then they
are also independent. For Z1 , Z2 to be uncorrelated then the following
equation should be satisfied
E[Z1 Z2 ] = E[Z1 ]E[Z2 ].
This implies
16a 47 = 8(a 2) = 8a = 31 = a =

31
.
8

For a given a, Z1 , Z2 are jointly Gaussian since they can be written as a

linear combination of jointly Gaussian random variables X, Y .

EE250 - Midterm 2 Practice Problems

13

Figure 7: Sample space

Problem 5. The continuous random variables have a joint pdf given by
{
C
if (x, y) belongs to the shaded region
fX,Y (x, y) =
0
o.w.
Find C such fX,Y (x, y) is a valid pdf.
Solution:

fX,Y (x, y)dxdy = 1.

Cdydx +
0

Cdydx = 1.

x1

Then,
C = 1/2.
Find fX (x)
Solution:

fX (x) =

f (x, y)dy.

{ 1
0.5dy = 0.5 0 x 1
fX (x) = x0
0.5dy = 0.5 1 < x 2
x1
Then,
fX (x) = 0.5,
Find fY |X (y|x)
Solution:
fY |X (y|x) =

0 x 2.

f (x, y)
.
fX (x)

(5)

EE250 - Midterm 2 Practice Problems

14

If 0 x 1, then
fY |X (y|x) = 0.5/0.5 = 1

0 y 1.

If 1 x 2, then
fY |X (y|x) = 0.5/0.5 = 1
Find E[Y |X = x]
Solution:

x 1 y x.

E[Y |X = x] =

yfY |X (y|x)dy.

If 0 x 1, then

E[Y |X = x] =

y1dy = 1/2.
0

If 1 x 2, then

E[Y |X = x] =

y1dy = x 1/2.
x1

Hence,

{
E[Y |X = x] =

1/2
0x1
x 1/2 1 x 2