HW Chapters 8

Problem I A random sample of 49 lunch customers was taken at a restaurant. The average amount of time the customers in the sample stayed in the restaurant was 33 minutes. From past experience, it is known that the standard deviation equals 10 minutes. a. b. Compute the standard error of the mean. x = / n = 10/ 49 = 1.42

What can be said about the sampling distribution for the average amount of time customers spent in the restaurant? Be sure to explain your answer. We use the standard error to measure how the mean varies with variation of data given the same quantity. We can say that the variation of the sample means for 49 samples is much less than variation in the population because Standard error < Standard deviation. c. With a .95 probability, what statement can be made about the size of the margin of error? If there are 10 different samples of 49 customers, from the same population, we would find that 9.5 of these samples would yield a result within our margin of error: n which is equal to : Z /2 * / n= 1.96 *10 /7 = 2.8. The amount of imprecision in the estimate is : 2.8 d. Construct a 95% confidence interval for the true average amount of time customers spent in the restaurant.

* The lower bound: 33 - 1.96*10/7 = 30.2 * The upper bound: 33 + 1.96*10/7 = 35.8 30.2 <= <= 35.9 e. With a .95 probability, how large of a sample would have to be taken to provide a margin of error of 2.5 minutes or less?

3.8416*100/6.25 = 61.46 n = 62

Problem II A random sample of 36 magazine subscribers is taken to estimate the mean age of all subscribers. The data follow. Use Excel to construct a 90% confidence interval estimate of the mean age of all of this magazines subscribers. Subscriber Age Subscriber Age Subscriber Age 1 39 13 40 25 38 2 27 14 35 26 51 3 38 15 35 27 26 4 33 16 41 28 39 5 40 17 34 29 35 6 35 18 46 30 37 7 51 19 44 31 33 8 36 20 44 32 41 9 50 21 43 33 36 10 28 22 32 34 33 11 33 23 29 35 46 12 35 24 33 36 37

Using Excel, we have:

Problem III A university planner wants to determine the proportion of spring semester students who will attend summer school. She surveys 32 current students discovering that 12 will return for summer school. a. Construct a 90% confidence interval estimate for the proportion of current spring students who will return for summer school. P= 12/32= 0.37 0.37 - 1.645 ( 0.37*0.63 /32) < < 0.37 + 1.645 ( 0.37*0.63 /32) 0.2296 < <0.5104 b. With a 0.95 probability, how large of a sample would have to be taken to provide a margin of error of 3% or less? n= (1.96) ( 0.37) ( 0.67) / (0.03) = 3.84 * 0.23 / 0.0009 = 981.33 n= 982

Problem IV A real estate agent wants to estimate the mean selling price of two-bedroom homes in a particular area. She wants to estimate the mean selling price to within $10,000 with an 89.9% level of confidence. The standard deviation of selling prices is unknown but the agent estimates that the highest selling price is $1,000,000 and the lowest is $50,000. How many homes should be sampled?

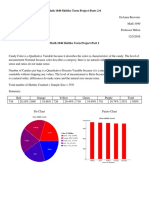
Problem V It is known that the variance of a population equals 484. A random sample of 81 observations is going to be taken from the population. a. With a .80 probability, what statement can be made about the size of the margin of error? Variance = 484, n = 81, SD: 22 e = Z a/2 * / n = 1.28* 22/9 = 3.21 The amount of imprecision in the sampling equals 3.21 b. With a .80 probability, how large of a sample would have to be taken to provide a margin of error of 3 or less? n= ( 1.28) * (22)/ 3 = 88 Problem VI A new brand of breakfast cereal is being market tested. One hundred boxes of the cereal were given to consumers to try. The consumers were asked whether they liked or disliked the cereal. You are given their responses below. Response Frequency 60 40 100 a. What is the point estimate of the proportion of people who will like the cereal? Liked = 60/100 = 0.6 b. Construct a 95% confidence interval for the proportion of all consumers who will like the cereal. p- Z a/2 * ( p (1-p) /n) <P< p+Z a/2 * ( p (1-p) /n) 0.6 (1.96 *( 0.4*0.6/100) < P< 0.6 + (1.96 *( 0.4*0.6/100) 0.5040 < P< 0.6047 c. What is the margin of error for the 95% confidence interval that you constructed in part b? e = 1.96 * ( 0.6*0.4/100) = 0.0960 d. With a .95 probability, how large of a sample needs to be taken to provide a margin of error of .09 or less? = 1.96 0.6*0.4 / 0.09 = 113.77
n= 114

Liked Disliked