Beruflich Dokumente
Kultur Dokumente
Mathcad - Extra8
Hochgeladen von
Desejo SozinandoOriginalbeschreibung:
Originaltitel
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Mathcad - Extra8
Hochgeladen von
Desejo SozinandoCopyright:
Verfügbare Formate
Computer Programming Skills MathCad Solution by DF Sozinando
Student at the Vaal University of
Technology
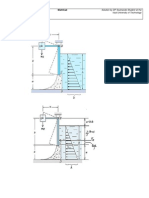
*The semicylindrical shell of mass m and radius r is rolled through an angle by the horizontal
force P applied to its rim. If the coeficient of friction is
s
, determine the angle at which the
shell slips on the horizontal surfuce as P is gradually increased. What value of
s
will permit to
reach 90
o
and plot the graph to investigate the coefficient of friction when change the angle
0 s 90 s .
TIP:
1. Redraw the figure and O is the point of coordinates (0,0). It is essential to draw the OX ,
OY cartesians axes and negligible OZ axes. D is the center of the full circle D will thus be
vertically aligned with O. D is a point of coordinates (0,r). G is the centre of gravity of half
circle, with coordinates.
2. Normal force used for the frictional force is mg-P; multiplying density and volume results
into the mass.
Solution:
Computer Programming Skills MathCad Solution by DF Sozinando
Student at the Vaal University of
Technology
1. Force direction of the respective points:
a
4 r
3
= from semi-circular Area Centre of Gravi ty
A
r - cos ( )
r r sin ( ) +
0
|
\
|
|
|
.
= B
r cos ( )
r r sin ( ) -
0
|
\
|
|
|
.
= D
0
r
0
|
\
|
|
|
.
= G
4 - r
3
sin ( )
r
4 r
3
cos ( ) -
0
|
\
|
|
|
|
|
|
.
=
2. Developing Equation of horizontal equilibrium (Deriving an expression for P):
Horizontal Forces: P F
- 0 = F
m g ( ) = m
2
r
2
t =
P
2
r
2
t g
|
\
|
|
.
- 0 = solve for P it's will be:
P
g r
2
t
2
=
3. Equation Equilibrium of moments about O (Deriving an expression for P):
symbolic evalueting this
equation its will be:
r - cos ( )
r r sin ( ) +
0
|
\
|
|
|
.
P
0
0
|
\
|
|
|
.
4 - r
3
sin ( )
r
4 r
3
cos ( ) -
0
|
\
|
|
|
|
|
|
.
0
2
- r
2
t g
0
|
\
|
|
|
|
|
.
+
2 g r
3
t sin ( )
3
P r r sin ( ) + ( ) - 0 = solve for P its will be:
P
2 g r
2
t sin ( )
3 sin ( ) 3 +
=
Computer Programming Skills MathCad Solution by DF Sozinando
Student at the Vaal University of
Technology
4. Deriving an expression for coefficient of friction as a funtion of angle:
P
static
P
kinematic
=
g r
2
t
2
2 g r
2
t sin ( )
3 sin ( ) 3 +
= solve for it's will be:
( )
4 sin ( )
3 sin ( ) 3 + ( )
:=
90deg ( ) 0.212 =
0 20 40 60 80
0
0.1
0.2
( )
deg
Das könnte Ihnen auch gefallen
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeVon EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeBewertung: 4 von 5 Sternen4/5 (5795)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreVon EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreBewertung: 4 von 5 Sternen4/5 (1090)
- Never Split the Difference: Negotiating As If Your Life Depended On ItVon EverandNever Split the Difference: Negotiating As If Your Life Depended On ItBewertung: 4.5 von 5 Sternen4.5/5 (838)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceVon EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceBewertung: 4 von 5 Sternen4/5 (895)
- Grit: The Power of Passion and PerseveranceVon EverandGrit: The Power of Passion and PerseveranceBewertung: 4 von 5 Sternen4/5 (588)
- Shoe Dog: A Memoir by the Creator of NikeVon EverandShoe Dog: A Memoir by the Creator of NikeBewertung: 4.5 von 5 Sternen4.5/5 (537)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersVon EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersBewertung: 4.5 von 5 Sternen4.5/5 (345)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureVon EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureBewertung: 4.5 von 5 Sternen4.5/5 (474)
- Her Body and Other Parties: StoriesVon EverandHer Body and Other Parties: StoriesBewertung: 4 von 5 Sternen4/5 (821)
- The Emperor of All Maladies: A Biography of CancerVon EverandThe Emperor of All Maladies: A Biography of CancerBewertung: 4.5 von 5 Sternen4.5/5 (271)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Von EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Bewertung: 4.5 von 5 Sternen4.5/5 (121)
- The Little Book of Hygge: Danish Secrets to Happy LivingVon EverandThe Little Book of Hygge: Danish Secrets to Happy LivingBewertung: 3.5 von 5 Sternen3.5/5 (400)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyVon EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyBewertung: 3.5 von 5 Sternen3.5/5 (2259)
- The Yellow House: A Memoir (2019 National Book Award Winner)Von EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Bewertung: 4 von 5 Sternen4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaVon EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaBewertung: 4.5 von 5 Sternen4.5/5 (266)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryVon EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryBewertung: 3.5 von 5 Sternen3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnVon EverandTeam of Rivals: The Political Genius of Abraham LincolnBewertung: 4.5 von 5 Sternen4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealVon EverandOn Fire: The (Burning) Case for a Green New DealBewertung: 4 von 5 Sternen4/5 (74)
- The Unwinding: An Inner History of the New AmericaVon EverandThe Unwinding: An Inner History of the New AmericaBewertung: 4 von 5 Sternen4/5 (45)
- Mathcad - Extra43Dokument1 SeiteMathcad - Extra43Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra41Dokument2 SeitenMathcad - Extra41Desejo SozinandoNoch keine Bewertungen
- Bradford Protein-Determination of Milk ProteinDokument3 SeitenBradford Protein-Determination of Milk Proteinanitram yo50% (2)
- Mathcad - Beam ProgrammingDokument1 SeiteMathcad - Beam ProgrammingDesejo SozinandoNoch keine Bewertungen
- Mathcad - Test 2Dokument2 SeitenMathcad - Test 2Desejo SozinandoNoch keine Bewertungen
- Gyrops 22 08 2016Dokument7 SeitenGyrops 22 08 2016Desejo SozinandoNoch keine Bewertungen
- Mathcad - Test 1Dokument3 SeitenMathcad - Test 1Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra40Dokument1 SeiteMathcad - Extra40Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra33Dokument1 SeiteMathcad - Extra33Desejo Sozinando50% (2)
- Mathcad - Extra42Dokument2 SeitenMathcad - Extra42Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra39Dokument1 SeiteMathcad - Extra39Desejo Sozinando100% (1)
- Mathcad - Extra38Dokument2 SeitenMathcad - Extra38Desejo Sozinando0% (1)
- Mathcad - Extra37Dokument2 SeitenMathcad - Extra37Desejo Sozinando0% (1)
- Mathcad - Extra36Dokument2 SeitenMathcad - Extra36Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra35Dokument2 SeitenMathcad - Extra35Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra31Dokument1 SeiteMathcad - Extra31Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra28Dokument3 SeitenMathcad - Extra28Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra29Dokument1 SeiteMathcad - Extra29Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra25Dokument1 SeiteMathcad - Extra25Desejo Sozinando0% (1)
- Mathcad - Extra20Dokument1 SeiteMathcad - Extra20Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra26Dokument1 SeiteMathcad - Extra26Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra13Dokument1 SeiteMathcad - Extra13Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra12Dokument2 SeitenMathcad - Extra12Desejo SozinandoNoch keine Bewertungen
- Mathcad - Extra18Dokument2 SeitenMathcad - Extra18Desejo Sozinando0% (1)
- Mathcad - Extra21Dokument2 SeitenMathcad - Extra21Desejo SozinandoNoch keine Bewertungen
- Vidyakankar Rotational MechanicsDokument4 SeitenVidyakankar Rotational MechanicsVikalp JoshiNoch keine Bewertungen
- Types of MeteoritesDokument2 SeitenTypes of MeteoritesJoel SamsonNoch keine Bewertungen
- Pipeline Corrosion Management CapabilityDokument2 SeitenPipeline Corrosion Management CapabilityMajdi Abdulrahman Mohamed RahamaNoch keine Bewertungen
- Lab Exercise # 6 - Cell Membrane TransportDokument4 SeitenLab Exercise # 6 - Cell Membrane TransportMei KurunoNoch keine Bewertungen
- Phy 9th CH 1 To 4Dokument4 SeitenPhy 9th CH 1 To 4Hameedashiq7 AshiqhameedNoch keine Bewertungen
- Lab 4 Buffers PDFDokument7 SeitenLab 4 Buffers PDFZiana ManzarNoch keine Bewertungen
- Tutorial (Annotated) 1.2 MotionDokument8 SeitenTutorial (Annotated) 1.2 Motionliming chenNoch keine Bewertungen
- Testing The Hardness of WaterDokument3 SeitenTesting The Hardness of Wateralexduart01Noch keine Bewertungen
- Design of Industrial Gravity Type Separators For The Hydrocarbons and Heavy Oil-Water SeparationsDokument5 SeitenDesign of Industrial Gravity Type Separators For The Hydrocarbons and Heavy Oil-Water SeparationsCandraNoch keine Bewertungen
- 10 1021@acs Iecr 9b02077Dokument14 Seiten10 1021@acs Iecr 9b02077dipen royNoch keine Bewertungen
- Stoichiometric CalculationsDokument33 SeitenStoichiometric CalculationsHazrati Ummi100% (1)
- Chemistry and Electricity:: ElectrochemistryDokument5 SeitenChemistry and Electricity:: ElectrochemistrySuleman TariqNoch keine Bewertungen
- SSPC News Bulletin - July 2020Dokument26 SeitenSSPC News Bulletin - July 2020JlkKumarNoch keine Bewertungen
- Crystallization of Al-Si Alloys in The Course of High Pressure Die-CastingDokument8 SeitenCrystallization of Al-Si Alloys in The Course of High Pressure Die-CastingHandri GustiarNoch keine Bewertungen
- 9702 Quantum Physics AllDokument13 Seiten9702 Quantum Physics AllSwifty SpotNoch keine Bewertungen
- How A Photon Is Created or AbsorbedDokument5 SeitenHow A Photon Is Created or AbsorbedLucia LopezNoch keine Bewertungen
- Find Your Way Around The SkiesDokument3 SeitenFind Your Way Around The SkiesgamangabrielNoch keine Bewertungen
- Spatial Light Modulator (SLM) As An Optical SwitchDokument27 SeitenSpatial Light Modulator (SLM) As An Optical SwitchAnonymous Lb76XTTnNoch keine Bewertungen
- Theoretical and Experimental Simulation of Passive Vacuum Solar FDokument290 SeitenTheoretical and Experimental Simulation of Passive Vacuum Solar FBelchior Ferreira PintoNoch keine Bewertungen
- Chemical Kinetics and Catalysis: Richard I: MaselDokument7 SeitenChemical Kinetics and Catalysis: Richard I: MaselShiv KumarNoch keine Bewertungen
- Aoc Lab 2Dokument4 SeitenAoc Lab 2rohan NathNoch keine Bewertungen
- D 819Dokument56 SeitenD 819ksvinyk7193Noch keine Bewertungen
- Chapter 4 - Introduction To Remote SensingDokument85 SeitenChapter 4 - Introduction To Remote SensingFaizan Ahmad FASTNUNoch keine Bewertungen
- Winsem2012 13 Cp0401 28 Mar 2013 Rm01 Temperature TransducersDokument35 SeitenWinsem2012 13 Cp0401 28 Mar 2013 Rm01 Temperature TransducersKaushik ReddyNoch keine Bewertungen
- Effect of Chloride Ions On The Corrosion of Galvanized Steel Embedded in Concrete Prepared With Cements of Different CompositionDokument13 SeitenEffect of Chloride Ions On The Corrosion of Galvanized Steel Embedded in Concrete Prepared With Cements of Different CompositionAbubakar Yakubu YakubuNoch keine Bewertungen
- Iso 20819 2018Dokument9 SeitenIso 20819 2018Rafid AriaNoch keine Bewertungen
- Positioning Techniques - Horizontal Vertical PDFDokument34 SeitenPositioning Techniques - Horizontal Vertical PDFMuhd Zuhairi100% (1)
- An Introduction To Organic Reactions and Their MechanismsDokument88 SeitenAn Introduction To Organic Reactions and Their MechanismsBurcu Gözde BilolNoch keine Bewertungen
- CHE 176 Complete SlideDokument606 SeitenCHE 176 Complete Slideolawandeilo123Noch keine Bewertungen