Beruflich Dokumente
Kultur Dokumente
Beta Distribution
Hochgeladen von
Hasrul ZahidOriginalbeschreibung:
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Beta Distribution
Hochgeladen von
Hasrul ZahidCopyright:
Verfügbare Formate
BETA DISTRIBUTION HISTORY The distribution has a very long history.
The "problem in the doctrine of chances" that Bayes treated produced a beta distribution for the posterior density of the probability of a success in Bernoulli trials. In the early 20th century English literature it was usual to refer to the distribution by its designation in the Pearson family of curves. However the new text-books of the 1940s did not favour the Pearson classification and the beta designation has become standard. An Essay towards solving a Problem in the Doctrine of Chances is a work on the mathematical theory of probability by the Reverend Thomas Bayes, published in 1763, two years after its author's death. It included a statement of a special case of what is now called Bayes' theorem. In 18th-century English, the phrase "doctrine of chances" meant the theory of probability. It had been introduced as the title of a book by Abraham Demoivre. Bayes supposed a sequence of independent experiments, each having as its outcome either success or failure, the probability of success being some number p between 0 and 1. But then he supposed p to be an uncertain quantity, whose probability of being in any interval between 0 and 1 is the length of the interval. In modern terms, p would be considered a random variable uniformly distributed between 0 and 1. Conditionally on the value of p, the trials resulting in success or failure are independent, but unconditionally (or "marginally") they are not. That is because if a large number of successes are observed, then p is more likely to be large, so that success on the next trial is more probable. The question Bayes addressed was: what is the conditional probability distribution of p, given the numbers of successes and failures so far observed. The answer is that its probability density function is
(and (p) = 0 for p < 0 or p > 1) where k is the number of successes so far observed, and n is the number of trials so far observed. This is what today is called the Beta distribution with parameters k + 1 and n k + 1.
P.D.F. OR P.F. Probability density function The probability density function of the beta distribution is:
where (z) is the gamma function. The beta function, B, appears as a normalization constant to ensure that the total probability integrates to unity. A random variable X that is Beta-distributed with shape and is denoted XBe(,) Cumulative distribution function The cumulative distribution function is
where Bx(,) is the incomplete beta function and Ix(,) is the regularized incomplete beta function
PARAMETER Parameter estimation Let
be the sample mean and
be the sample variance. The method-of-moments estimates of the parameters are
When the distribution is required over an interval other than [0, 1], say
, then replace
with
and
with
in the above equations.
There is no closed-form of the maximum likelihood estimates for the parameters. Reference:
EXAMPLE OF P.F. OR P.D.F. PLOT Probability density function
Cumulative distribution function
MEAN AND VARIANCE The expected value (mean) (), variance (second central moment), skewness (third central moment), and kurtosis excess (fourth central moment) of a Beta distribution random variable X with parameters and are:
The skewness is
The kurtosis excess is:
or:
In general, the kth raw moment is given by
where (x)k is a Pochhammer symbol representing rising factorial. It can also be written in a recursive form as
One can also show that
EXAMPLE 1 Important computational aids for the numerical evaluation of incomplete integrals of gamma and beta distributions involve expressing such integrals as sums of probabilities of particular Poisson and binomial distributions. a) Prove that
where b) Prove that and
and where is a positive integer.
where and are positive integers and where SOLUTION 1 a) With , we have
which is when .
b) With
, we have
Thus, since we have
which is when .
EXAMPLE 2 Let be a random sample of binary random variables with , show that a level . Using the confidence interval for
cumulative distribution function of is
where defined to be . SOLUTION 2 Since
is the
th quantile of the F-distribution
, and
is
has the binomial distribution with size
and probability
and the binomial family has , is decreasing is the solution to
monotone likelihood ratio in , the cumulative distribution function of in for fixed . A level and confidence interval for is . Let , where
is the solution to
be a random variable having
the beta distribution with parameter
. Using integral by parts, we obtain that
Therefore,
is the if
th quantile of the beta distribution with parameter . For , it is the solution to if .Then, . Hence,
if is the
and is equal to
th quantile of the beta distribution with parameter to if . Let be a random variable having the F-distribution . Hence
and is equal has
the beta distribution with parameter
when
is defined to be . Similarly,
Note that
has the F-distribution
. Hence,
Das könnte Ihnen auch gefallen
- Wise Use of Null Hypothesis Tests: A Practitioner's HandbookVon EverandWise Use of Null Hypothesis Tests: A Practitioner's HandbookNoch keine Bewertungen
- Multidimensional Mathematical Demography: Proceedings of the Conference on Multidimensional Mathematical Demography Held at the University of Maryland, College Park, Maryland, March 23-25, 1981, Sponsored by the National Science FoundationVon EverandMultidimensional Mathematical Demography: Proceedings of the Conference on Multidimensional Mathematical Demography Held at the University of Maryland, College Park, Maryland, March 23-25, 1981, Sponsored by the National Science FoundationNoch keine Bewertungen
- On The Use of Expert Judgement in The Qualification of Risk AssessmentDokument52 SeitenOn The Use of Expert Judgement in The Qualification of Risk AssessmentIrenataNoch keine Bewertungen
- Universiteit Hasselt Concepts in Bayesian Inference Exam June 2015Dokument8 SeitenUniversiteit Hasselt Concepts in Bayesian Inference Exam June 2015Nina MorgensternNoch keine Bewertungen
- Ch4 BootstrapDokument90 SeitenCh4 BootstrapDaniels PicturesNoch keine Bewertungen
- Ipc2022 - 87054 Probabilistic Flaw Growth Rate Estimates Using Multiple InlineDokument10 SeitenIpc2022 - 87054 Probabilistic Flaw Growth Rate Estimates Using Multiple InlineOswaldo MontenegroNoch keine Bewertungen
- Arellano - Quantile Methods PDFDokument10 SeitenArellano - Quantile Methods PDFInvestNoch keine Bewertungen
- Algorithms With JULIADokument447 SeitenAlgorithms With JULIALuis Felipe Quisbert QuispeNoch keine Bewertungen
- An Improved Method of Extreme Value AnalysisDokument7 SeitenAn Improved Method of Extreme Value AnalysisDevita MayasariNoch keine Bewertungen
- Heavy-Tail Phenomena - Probabilistic and Statistical Modeling - S. Resnick (Springer, 2007) WW PDFDokument410 SeitenHeavy-Tail Phenomena - Probabilistic and Statistical Modeling - S. Resnick (Springer, 2007) WW PDFSlava DubininNoch keine Bewertungen
- Statistical Computing by Using RDokument11 SeitenStatistical Computing by Using RChen-Pan Liao100% (1)
- Quantum Fractals - From Heisenberg's Uncertainty To Barnsley's Fractality (PDFDrive)Dokument358 SeitenQuantum Fractals - From Heisenberg's Uncertainty To Barnsley's Fractality (PDFDrive)stankgodNoch keine Bewertungen
- Exercises DobsonDokument3 SeitenExercises Dobsonvsuarezf27320% (1)
- UntitledDokument201 SeitenUntitledbill dollarNoch keine Bewertungen
- App.A - Detection and Estimation in Additive Gaussian Noise PDFDokument55 SeitenApp.A - Detection and Estimation in Additive Gaussian Noise PDFLê Dương LongNoch keine Bewertungen
- Bivariate Normal 1 With Answers PDFDokument22 SeitenBivariate Normal 1 With Answers PDFdNoch keine Bewertungen
- Non-Ergodicity and Its Implications For Businesses and Investors PDFDokument72 SeitenNon-Ergodicity and Its Implications For Businesses and Investors PDFAtul Divya SodhiNoch keine Bewertungen
- Solution 2Dokument4 SeitenSolution 2fra.public0% (1)
- Markov Chain Monte-Carlo ExplainedDokument12 SeitenMarkov Chain Monte-Carlo ExplainedJaella ANoch keine Bewertungen
- Diff in Diff Uk12 VillaDokument16 SeitenDiff in Diff Uk12 Villapcg20013793Noch keine Bewertungen
- Handbook Bio StatDokument305 SeitenHandbook Bio StatADWINDT100% (1)
- 2 Birth DeathDokument49 Seiten2 Birth Deathsumit2560% (1)
- Le Roux, B. & H. Rouanet (2010) Multiple Correspondance AnalysisDokument62 SeitenLe Roux, B. & H. Rouanet (2010) Multiple Correspondance AnalysisMalthe Øland RibeNoch keine Bewertungen
- GSEMModellingusingStata PDFDokument97 SeitenGSEMModellingusingStata PDFmarikum74Noch keine Bewertungen
- Lecture+14 SAS Bootstrap and JackknifeDokument12 SeitenLecture+14 SAS Bootstrap and JackknifeJoanne WongNoch keine Bewertungen
- Properties of The Trinomial DistributionDokument2 SeitenProperties of The Trinomial DistributionPerry01Noch keine Bewertungen
- Univariate, Bivariate and Multivariate Methods in Corpus-Based Lexicography - A Study of SynonymyDokument614 SeitenUnivariate, Bivariate and Multivariate Methods in Corpus-Based Lexicography - A Study of SynonymyAntti ArppeNoch keine Bewertungen
- Class 7Dokument42 SeitenClass 7rishabhNoch keine Bewertungen
- Design of Experiments - Week 1, 2Dokument50 SeitenDesign of Experiments - Week 1, 2Akram KhanNoch keine Bewertungen
- Goodness of Fit and Related Inference Processes For Quantile RegressionDokument16 SeitenGoodness of Fit and Related Inference Processes For Quantile RegressionAndersonMonteiroNoch keine Bewertungen
- Pure Birth ProcessesDokument13 SeitenPure Birth ProcessesDaniel Mwaniki100% (1)
- NEW Bayesian - Approaches.in - Oncology.using.R.and - OpenBUGSDokument260 SeitenNEW Bayesian - Approaches.in - Oncology.using.R.and - OpenBUGSnfbeusebio3962Noch keine Bewertungen
- Longitudinal PDFDokument664 SeitenLongitudinal PDFikin sodikinNoch keine Bewertungen
- Are Zero Inflated Distributions Compulsory in The Presence of Zero InflationDokument4 SeitenAre Zero Inflated Distributions Compulsory in The Presence of Zero InflationInternational Journal of Innovative Science and Research TechnologyNoch keine Bewertungen
- Probability DistributionsaDokument82 SeitenProbability Distributionsaasdasdas asdasdasdsadsasddssaNoch keine Bewertungen
- Dsur I Chapter 08 Logistic RegressionDokument41 SeitenDsur I Chapter 08 Logistic RegressionDannyNoch keine Bewertungen
- An Introduction To Malliavin Calculus With Applications To EconomicsDokument83 SeitenAn Introduction To Malliavin Calculus With Applications To EconomicsselivesNoch keine Bewertungen
- Ordinal and Multinomial ModelsDokument58 SeitenOrdinal and Multinomial ModelsSuhel Ahmad100% (1)
- Glmcourse 002Dokument55 SeitenGlmcourse 002Ben HarveyNoch keine Bewertungen
- Cheatsheet Midterms 2 - 3Dokument2 SeitenCheatsheet Midterms 2 - 3Chen YuyingNoch keine Bewertungen
- 07 - Natural Experiment (Part 2) PDFDokument90 Seiten07 - Natural Experiment (Part 2) PDFJoe23232232Noch keine Bewertungen
- Statistical Theory and Methodology in Science and EngineeringDokument607 SeitenStatistical Theory and Methodology in Science and EngineeringNelson IsraelNoch keine Bewertungen
- STAT 1520 NotesDokument61 SeitenSTAT 1520 NotesnojnfoNoch keine Bewertungen
- Creating A Live World Weather Map Using Shiny - by M. Makkawi - The Startup - MediumDokument40 SeitenCreating A Live World Weather Map Using Shiny - by M. Makkawi - The Startup - MediumDirga DanielNoch keine Bewertungen
- Applied Multivariate Statistical Analysis Solution Manual PDFDokument18 SeitenApplied Multivariate Statistical Analysis Solution Manual PDFALVYAN ARIFNoch keine Bewertungen
- Tutorial Part I Information Theory Meets Machine Learning Tuto - Slides - Part1Dokument46 SeitenTutorial Part I Information Theory Meets Machine Learning Tuto - Slides - Part1apdpjpNoch keine Bewertungen
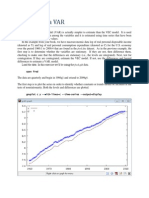
- Estimating A VAR - GretlDokument9 SeitenEstimating A VAR - Gretlkaddour7108Noch keine Bewertungen
- cs229 Notes1 PDFDokument28 Seitencs229 Notes1 PDFRichieQCNoch keine Bewertungen
- MCMC Sheldon RossDokument68 SeitenMCMC Sheldon RossMuhamadSukinNoch keine Bewertungen
- Cascade IndicatorsDokument72 SeitenCascade IndicatorsAna PalmaNoch keine Bewertungen
- (GAM) Application PDFDokument30 Seiten(GAM) Application PDFannisa rahmasariNoch keine Bewertungen
- 06 - Natural Experiment (Part 1) PDFDokument89 Seiten06 - Natural Experiment (Part 1) PDFJoe23232232Noch keine Bewertungen
- MA202 Probability Distributions, Transforms and Numerical MethodsDokument3 SeitenMA202 Probability Distributions, Transforms and Numerical MethodsSáçhìñDêvNoch keine Bewertungen
- (Springer Series in Statistics) R.-D. Reiss (Auth.) - Approximate Distributions of Order Statistics - With Applications To Nonparametric Statistics-Springer-Verlag New York (1989) PDFDokument362 Seiten(Springer Series in Statistics) R.-D. Reiss (Auth.) - Approximate Distributions of Order Statistics - With Applications To Nonparametric Statistics-Springer-Verlag New York (1989) PDFNicko Villar100% (1)
- Fernando, Logit Tobit Probit March 2011Dokument19 SeitenFernando, Logit Tobit Probit March 2011Trieu Giang BuiNoch keine Bewertungen
- ProbabilityDokument50 SeitenProbabilityssckp86Noch keine Bewertungen
- Bayesian Statistics For DummiesDokument5 SeitenBayesian Statistics For Dummiesjulianaruiz06Noch keine Bewertungen
- Order Statistics & Inference: Estimation MethodsVon EverandOrder Statistics & Inference: Estimation MethodsNoch keine Bewertungen
- Beta DistributionDokument9 SeitenBeta DistributionHasrul ZahidNoch keine Bewertungen
- Statistical InferenceDokument47 SeitenStatistical InferenceYoga RomdoniNoch keine Bewertungen
- Prospect Evaluation Fundamentals v1 0621Dokument58 SeitenProspect Evaluation Fundamentals v1 0621Lara FumarolaNoch keine Bewertungen
- Bayesian Nonparametrics and The Probabilistic Approach To ModellingDokument27 SeitenBayesian Nonparametrics and The Probabilistic Approach To ModellingTalha YousufNoch keine Bewertungen
- HW3 Molecular Polymorphism SolutionDokument2 SeitenHW3 Molecular Polymorphism SolutionMiriam KaufmanNoch keine Bewertungen
- Or-Mod 4Dokument35 SeitenOr-Mod 4Phone PeNoch keine Bewertungen
- Bayesian Networks - Exercises: 1 Independence and Conditional IndependenceDokument20 SeitenBayesian Networks - Exercises: 1 Independence and Conditional IndependenceCandy AngelNoch keine Bewertungen
- The Beta Distribution: Univariate DistributionsDokument7 SeitenThe Beta Distribution: Univariate Distributionsbig clapNoch keine Bewertungen
- Application of Project Evaluation, Review Technique and Critical Path Method (PERT-CPM) Model in Monitoring Building ConstructionDokument14 SeitenApplication of Project Evaluation, Review Technique and Critical Path Method (PERT-CPM) Model in Monitoring Building Constructiondinosaur x-drakeNoch keine Bewertungen
- DADM - Tools HelpDokument24 SeitenDADM - Tools HelpvaskoreNoch keine Bewertungen
- MinE424 - 05ControlOfProjects-CPM and PERT Methods (Part-1)Dokument46 SeitenMinE424 - 05ControlOfProjects-CPM and PERT Methods (Part-1)Ege UygunturkNoch keine Bewertungen
- Will YOUR Project Overrun? Do A Cost Risk Analysis: David T. Hulett, PH.DDokument30 SeitenWill YOUR Project Overrun? Do A Cost Risk Analysis: David T. Hulett, PH.Dleading_aliNoch keine Bewertungen
- Tuljaram Chaturchand College of Arts, Science and Commerce, BaramatiDokument20 SeitenTuljaram Chaturchand College of Arts, Science and Commerce, BaramatiLiban Ali MohamudNoch keine Bewertungen
- Introductory Probability Theory PDFDokument299 SeitenIntroductory Probability Theory PDFjrcg0914100% (1)
- Qing Wu 2006 - Cost Overrun Risk AnalysisDokument77 SeitenQing Wu 2006 - Cost Overrun Risk AnalysisTAHER AMMARNoch keine Bewertungen
- Probabilistic Programming: Marius Popescu 2018 - 2019Dokument42 SeitenProbabilistic Programming: Marius Popescu 2018 - 2019Filote CosminNoch keine Bewertungen
- Bookkeeping Functions: RandomDokument16 SeitenBookkeeping Functions: Randomlibin_paul_2Noch keine Bewertungen
- Enfsi DWGDokument148 SeitenEnfsi DWGjose.pradoNoch keine Bewertungen
- Statistical PERT Normal Edition Quick Start Guide For Version 4 UpdatedDokument17 SeitenStatistical PERT Normal Edition Quick Start Guide For Version 4 UpdatedMusa GürsoyNoch keine Bewertungen
- Mathematical Statistics With Applications in R 2nd Edition Ramachandran Solutions ManualDokument40 SeitenMathematical Statistics With Applications in R 2nd Edition Ramachandran Solutions Manualtaylorbatesozrxpikmwa100% (25)
- An Introduction To Bayesian StatisticsDokument20 SeitenAn Introduction To Bayesian Statisticsjamesyu100% (9)
- Beta RegDokument24 SeitenBeta RegreviurNoch keine Bewertungen
- Information About This Workbook: Author: Website: Relevant Links: ContactDokument64 SeitenInformation About This Workbook: Author: Website: Relevant Links: ContactZaman BajwaNoch keine Bewertungen
- A Reinforcement Learning Approach For Optimal Placement of Sensors in Protected Cultivation SystemsDokument20 SeitenA Reinforcement Learning Approach For Optimal Placement of Sensors in Protected Cultivation Systems鍾孟哲Noch keine Bewertungen
- Beta Regression Modeling: Recent Advances in Theory and ApplicationsDokument51 SeitenBeta Regression Modeling: Recent Advances in Theory and ApplicationsmuralidharanNoch keine Bewertungen
- ISM Chapter6Dokument22 SeitenISM Chapter6Jeans Carlos100% (1)
- Oksanen Minchin 2002 Along Ecological GradientsDokument11 SeitenOksanen Minchin 2002 Along Ecological GradientsMilton CordovaNoch keine Bewertungen
- Paper-Weibull Analysis Using R in A NutshellDokument7 SeitenPaper-Weibull Analysis Using R in A NutshellMubangaNoch keine Bewertungen
- Chapter 4Dokument36 SeitenChapter 4Sumedh KakdeNoch keine Bewertungen
- Load Balance GHTDokument12 SeitenLoad Balance GHTKank RiyanNoch keine Bewertungen