Beruflich Dokumente
Kultur Dokumente
Tessellation Project
Hochgeladen von
Nicholas YatesCopyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Tessellation Project
Hochgeladen von
Nicholas YatesCopyright:
Verfügbare Formate
Tessellation Project Names _____________________________
Mr. Yates Date ___________ Geometry Period ____
Two people to a group.
Cut templates out of index card based on the polygons on p. 398.
You should make:
Shape (# sides) # to cut
Triangles (3) 6
Squares (4) 4
Pentagons (5) 3
Hexagons (6) 3
Octagons (8) 2
Decagons (10) 2
Dodecagons (12) 2
I. First investigate which shapes will allow a regular tiling of the plane—that is,
which shapes will fit together to fill up space, using only copies of one type of
shape?
For each regular tiling you find, on graph paper, draw a copy of one vertex
which has 360 degrees of one shape fitting around it.
II. Now investigate which pairs or triplets of shapes can fit together (for example,
two dodecagons and a triangle fill a vertex; this tiling is illustrated on p.397 as
3.12.12). The results of such vertices fitting together ad infinitum is called a
semiregular tessellation of the plane. Try to find as many combinations as
you can (there are eight), and draw a copy of each vertex on graph paper.
III. Pick one regular tiling and one semiregular tiling, and fill up a sheet of graph
paper with each. After you do the following analysis, please make them
colorful, so that I may hang them up on my Student Work wall!
For each tiling:
1) Are there any translations that move shapes on top of other copies of the
same shape? Draw in three arrows in dark ink that indicate the length and
direction for these translations. Your tiling has translation symmetry.
2) Are there any lines you can fold along to match up everything on both sides
of the line? Do the folds, then trace over them lightly with a pencil. Try and
get at least one fold from every possible direction (that is, non-parallel folds).
These folds indicate lines of reflection symmetry.
3) Are there any points of rotation symmetry, where you can turn the whole
picture around that point and every piece will match up with a
corresponding piece around it? Draw in dark ink at least four of these points.
4) Bonus: identify with lines and arrows any glide reflections on the back.
5) Name it. Go back and name each of your eleven vertices from Parts I & II.
Naming tilings that are semiregular like this can be accomplished by just
listing all the shapes that meet at a vertex. For example, if 6 triangles meet at
every vertex, we can write 3.3.3.3.3.3 (3’s since each triangle has three sides).
6) Color in your tessellation.
IV. Cut out a square from index-card stock. Mr. Yates will show you how to
create a shape by cutting and taping pieces from your square. Use this shape
to create an Escher-esque tiling of the plane.
V. Write one paragraph that identifies what you learned, what you found
interesting, and what you found difficult or frustrating about this project.
Your paragraph should have at least six sentences.
Grading rubric:
Part I – 10 points (got all 3 regular tilings; drew a copy of each vertex; named
each vertex/tiling)
Part II – 15 points (got all 8 semiregular tilings; drew a copy of each vertex;
named each vertex/tiling)
Part III – 25 points regular, 25 points semiregular (correct and colorful tiling;
reflections, rotations, translations identified; correct name)
Part IV – 15 points (for complete and colorful tiling)
Part V – 15 points (at least six sentences; addresses each topic)
105 points total possible
Das könnte Ihnen auch gefallen
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryVon EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryBewertung: 3.5 von 5 Sternen3.5/5 (231)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Von EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Bewertung: 4.5 von 5 Sternen4.5/5 (119)
- Never Split the Difference: Negotiating As If Your Life Depended On ItVon EverandNever Split the Difference: Negotiating As If Your Life Depended On ItBewertung: 4.5 von 5 Sternen4.5/5 (838)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaVon EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaBewertung: 4.5 von 5 Sternen4.5/5 (265)
- The Little Book of Hygge: Danish Secrets to Happy LivingVon EverandThe Little Book of Hygge: Danish Secrets to Happy LivingBewertung: 3.5 von 5 Sternen3.5/5 (399)
- Grit: The Power of Passion and PerseveranceVon EverandGrit: The Power of Passion and PerseveranceBewertung: 4 von 5 Sternen4/5 (587)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyVon EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyBewertung: 3.5 von 5 Sternen3.5/5 (2219)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeVon EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeBewertung: 4 von 5 Sternen4/5 (5794)
- Team of Rivals: The Political Genius of Abraham LincolnVon EverandTeam of Rivals: The Political Genius of Abraham LincolnBewertung: 4.5 von 5 Sternen4.5/5 (234)
- Shoe Dog: A Memoir by the Creator of NikeVon EverandShoe Dog: A Memoir by the Creator of NikeBewertung: 4.5 von 5 Sternen4.5/5 (537)
- The Emperor of All Maladies: A Biography of CancerVon EverandThe Emperor of All Maladies: A Biography of CancerBewertung: 4.5 von 5 Sternen4.5/5 (271)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreVon EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreBewertung: 4 von 5 Sternen4/5 (1090)
- Her Body and Other Parties: StoriesVon EverandHer Body and Other Parties: StoriesBewertung: 4 von 5 Sternen4/5 (821)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersVon EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersBewertung: 4.5 von 5 Sternen4.5/5 (344)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceVon EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceBewertung: 4 von 5 Sternen4/5 (894)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureVon EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureBewertung: 4.5 von 5 Sternen4.5/5 (474)
- The Unwinding: An Inner History of the New AmericaVon EverandThe Unwinding: An Inner History of the New AmericaBewertung: 4 von 5 Sternen4/5 (45)
- The Yellow House: A Memoir (2019 National Book Award Winner)Von EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Bewertung: 4 von 5 Sternen4/5 (98)
- On Fire: The (Burning) Case for a Green New DealVon EverandOn Fire: The (Burning) Case for a Green New DealBewertung: 4 von 5 Sternen4/5 (73)
- Well CompletionDokument26 SeitenWell Completionnitesh kumarNoch keine Bewertungen
- ACL Injuries in The Female Athlete: Causes, Impacts, and Conditioning Programs Frank R. Noyes Sue Barber-WestinDokument658 SeitenACL Injuries in The Female Athlete: Causes, Impacts, and Conditioning Programs Frank R. Noyes Sue Barber-WestinluizamgoNoch keine Bewertungen
- Gini Index Student HandoutDokument8 SeitenGini Index Student HandoutNicholas Yates100% (1)
- Bar BendingDokument142 SeitenBar Bendingjaffna100% (4)
- Bus Network Topology GuideDokument8 SeitenBus Network Topology GuideMjjames Manalo100% (1)
- Tensile FinalDokument43 SeitenTensile Finalnamrataavyas75% (4)
- Effect of Restraint, Volume Change, and Reinforcement On Cracking of Mass ConcreteDokument26 SeitenEffect of Restraint, Volume Change, and Reinforcement On Cracking of Mass ConcreteDIDIER ANGEL LOPEZ RINCONNoch keine Bewertungen
- STEM AnnualChallenge2011Dokument4 SeitenSTEM AnnualChallenge2011Nicholas YatesNoch keine Bewertungen
- A2TQuiz7 8 9 10 11 12Dokument2 SeitenA2TQuiz7 8 9 10 11 12Nicholas YatesNoch keine Bewertungen
- Phi ProjectDokument4 SeitenPhi ProjectNicholas YatesNoch keine Bewertungen
- A2T Final Exam 11 FormulaeDokument2 SeitenA2T Final Exam 11 FormulaeNicholas YatesNoch keine Bewertungen
- A2TQuizP3 P5 1 2 3 5 6 A1Dokument2 SeitenA2TQuizP3 P5 1 2 3 5 6 A1Nicholas YatesNoch keine Bewertungen
- Big Picture Ideas in A2TDokument1 SeiteBig Picture Ideas in A2TNicholas YatesNoch keine Bewertungen
- Bridge GeometryDokument1 SeiteBridge GeometryNicholas YatesNoch keine Bewertungen
- Green Eggs & Catch: The RulesDokument4 SeitenGreen Eggs & Catch: The RulesNicholas YatesNoch keine Bewertungen
- A2TQuizP1 P2 P3 P4 P5 P6Dokument2 SeitenA2TQuizP1 P2 P3 P4 P5 P6Nicholas YatesNoch keine Bewertungen
- A2T4QuizP3 6 7 8 9Dokument3 SeitenA2T4QuizP3 6 7 8 9Nicholas YatesNoch keine Bewertungen
- A2T4QuizP1 P2 P3 P4 P5 P6Dokument3 SeitenA2T4QuizP1 P2 P3 P4 P5 P6Nicholas YatesNoch keine Bewertungen
- A2T4QuizP5 P6 1 2 A1Dokument3 SeitenA2T4QuizP5 P6 1 2 A1Nicholas YatesNoch keine Bewertungen
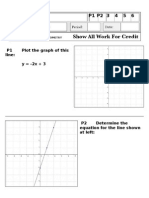
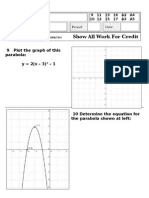
- Mr. Yates: 270° Coordinates: (,) 105° Coordinates: (,) A Graph: B GraphDokument3 SeitenMr. Yates: 270° Coordinates: (,) 105° Coordinates: (,) A Graph: B GraphNicholas YatesNoch keine Bewertungen
- A2TQuizP1 P2 3 4 5 6Dokument2 SeitenA2TQuizP1 P2 3 4 5 6Nicholas YatesNoch keine Bewertungen
- A2TQuiz9 10 11 12 13 15 16 17 A2 A3 A4 A5Dokument4 SeitenA2TQuiz9 10 11 12 13 15 16 17 A2 A3 A4 A5Nicholas YatesNoch keine Bewertungen
- A2T4MiniQuiz10 11Dokument1 SeiteA2T4MiniQuiz10 11Nicholas YatesNoch keine Bewertungen
- A2TQuiz7 8 9 10 11 12Dokument2 SeitenA2TQuiz7 8 9 10 11 12Nicholas YatesNoch keine Bewertungen
- A2TSkillsHandout AllDokument4 SeitenA2TSkillsHandout AllNicholas YatesNoch keine Bewertungen
- Algebra 2 With Trigonometry SyllabusDokument3 SeitenAlgebra 2 With Trigonometry SyllabusNicholas Yates0% (1)
- Mr. Yates: Lgebra With RigonometryDokument3 SeitenMr. Yates: Lgebra With RigonometryNicholas YatesNoch keine Bewertungen
- Mr. Yates: Lgebra With RigonometryDokument3 SeitenMr. Yates: Lgebra With RigonometryNicholas YatesNoch keine Bewertungen
- A2T4Quiz1 2 3 4 5Dokument3 SeitenA2T4Quiz1 2 3 4 5Nicholas YatesNoch keine Bewertungen
- A2TSkillsHandout SkillsGradingDokument2 SeitenA2TSkillsHandout SkillsGradingNicholas YatesNoch keine Bewertungen
- A2TSkillsHandout Analysis CoreDokument1 SeiteA2TSkillsHandout Analysis CoreNicholas YatesNoch keine Bewertungen
- A2TSkillsHandout Analysis P+ADokument1 SeiteA2TSkillsHandout Analysis P+ANicholas YatesNoch keine Bewertungen
- A2TSkillsHandout Algebra P+ADokument1 SeiteA2TSkillsHandout Algebra P+ANicholas YatesNoch keine Bewertungen
- WindmillDokument1 SeiteWindmillNicholas YatesNoch keine Bewertungen
- A2TSkillsHandout Algebra CoreDokument1 SeiteA2TSkillsHandout Algebra CoreNicholas YatesNoch keine Bewertungen
- POE FMP The Paper Tower BlankDokument1 SeitePOE FMP The Paper Tower BlankNicholas YatesNoch keine Bewertungen
- IgE Level Effect of Phyllanthus Acidus Leaf ExtractDokument5 SeitenIgE Level Effect of Phyllanthus Acidus Leaf Extractkhatami muhammadNoch keine Bewertungen
- QST HamClockDokument3 SeitenQST HamClockCPC PHCNoch keine Bewertungen
- METAL CLUSTER COMPLEXESDokument13 SeitenMETAL CLUSTER COMPLEXESKeybateNoch keine Bewertungen
- Phase Shift of 180 Degrees On Reflection From Optically Denser MediumDokument1 SeitePhase Shift of 180 Degrees On Reflection From Optically Denser MediumGreato HibernatoNoch keine Bewertungen
- Chm580 Experiment 3Dokument9 SeitenChm580 Experiment 3ohhiNoch keine Bewertungen
- Project PPTDokument47 SeitenProject PPTIshant KumawatNoch keine Bewertungen
- This Study Resource Was: Titration Level 1Dokument4 SeitenThis Study Resource Was: Titration Level 1Camaya RumbleNoch keine Bewertungen
- 5437 1Dokument190 Seiten5437 1Khateeb RehmanNoch keine Bewertungen
- Structural Soils Engineer's Quick Reference GuideDokument64 SeitenStructural Soils Engineer's Quick Reference GuideGreg McNamaraNoch keine Bewertungen
- Computer Science Project On Management SystemDokument26 SeitenComputer Science Project On Management Systemsajid aliNoch keine Bewertungen
- 01 - Lesson Plan - Fractions - Decimal - PercentDokument4 Seiten01 - Lesson Plan - Fractions - Decimal - PercentAnthony MontoyaNoch keine Bewertungen
- Hibbeler D14 e CH 12 P 23Dokument2 SeitenHibbeler D14 e CH 12 P 23Mona fabrigarNoch keine Bewertungen
- Akvola Technologies MicroGas S Technical Specifications - Web PDFDokument2 SeitenAkvola Technologies MicroGas S Technical Specifications - Web PDFHardik VavdiyaNoch keine Bewertungen
- Areas Related To CircleDokument32 SeitenAreas Related To CircleGiorno GiovannaNoch keine Bewertungen
- Datasheet PDFDokument16 SeitenDatasheet PDFSergio Daniel BarretoNoch keine Bewertungen
- TVS Apache RTR 180 Service ManualDokument25 SeitenTVS Apache RTR 180 Service ManualSandino JoseNoch keine Bewertungen
- Problems On Heat Transfer ConductionDokument3 SeitenProblems On Heat Transfer ConductionGenerale, Rey marck C.Noch keine Bewertungen
- LP Galvo Scanner LaserphotoDokument16 SeitenLP Galvo Scanner LaserphotoCostin DinamaxNoch keine Bewertungen
- IT407 Knowledge EngineeringDokument2 SeitenIT407 Knowledge EngineeringVidya ANoch keine Bewertungen
- Sabp G 007Dokument8 SeitenSabp G 007Li PengNoch keine Bewertungen
- Indicate The Answer Choice That Best Completes The Statement or Answers The QuestionDokument10 SeitenIndicate The Answer Choice That Best Completes The Statement or Answers The QuestionHasan EserNoch keine Bewertungen
- Tecquipment - Flumes - Data SheetDokument3 SeitenTecquipment - Flumes - Data SheetArthur BritoNoch keine Bewertungen
- Notes On Continuum MechanicsDokument13 SeitenNotes On Continuum Mechanicsdalves31503Noch keine Bewertungen
- PDCT - Hydraulic Torque Wrench - Hangzhou Penad Machinery Co.,LtdDokument4 SeitenPDCT - Hydraulic Torque Wrench - Hangzhou Penad Machinery Co.,LtdQS BMDSNoch keine Bewertungen