MA261-A Calculus III

2006 Fall
Homework 11 Solutions
Due 11/20/2006 8:00AM
12.6 #2 Find the area of the surface which is the part of the plane 2x + 5y + z = 10 that lies
inside the cylinder x
2
+ y
2
= 9.
[Solution]
Let D be the disk x
2
+y
2
9 on the xy-plane. We can write z = 102x5y = f (x; y).
So, our surface is a graph of the function f. Thus, the area is
A(S) =
__
D
_
1 +
_
@z
@x
_
2
+
_
@z
@y
_
2
dA =
__
D
_
1 + (2)
2
+ (5)
2
dA =
__
D
p
30dA
=
p
30
__
D
dA =
p
30A(D) .
The area of D is 3
2
= 9 since D is a disk with radius 3. Therefore, we have the surface
area is A(S) =
p
30 (9) = 9
p
30.

12.6 #4 Find the area of the surface which is the part of the plane with vector equation
r (u; v) = h1 + v; u 2v; 3 5u + vi
that is given by 0 u 1, 0 v 1.
[Solution]
We have
r
u
(u; v) = h0; 1; 5i
and
r
v
(u; v) = h1; 2; 1i .
To calculate the surface, we calculate jr
u
r
v
j rst.
jr
u
r
v
j =

i j k
0 1 5
1 2 1

= j9i 5j + (1) kj =
_
(9)
2
+ (5)
2
+ (1)
2
=
p
107.
Thus, the surface area is
A(S) =
__
D
jr
u
r
v
j dA =
__
D
p
107dA =
p
107
__
D
dA =
p
107
_
1
0
_
1
0
dudv =
p
107.

1
2
12.6 #6 Find the surface area which is the part of the surface z = 1 + 3x + 2y
2
that lies above
the triangle with vertices (0; 0), (0; 1), and (2; 1).
[Solution]
First, we recognize that the triangle D is a right angle triangle enclosed by x = 0,
y = 1, and x = 2y. Then, it can be described as 0 y 1 and 0 x 2y.
We can write z = 1 + 3x + 2y
2
= f (x; y). So, our surface is a graph of the function f.
Thus, the area is
A(S) =
__
D
_
1 +
_
@z
@x
_
2
+
_
@z
@y
_
2
dA =
__
D
_
1 + (3)
2
+ (4y)
2
dA
=
__
D
_
10 + 16y
2
dA =
_
1
0
_
2y
0
_
10 + 16y
2
dxdy
=
_
1
0
2y
_
10 + 16y
2
dy
u=10+16y
2
=
_
26
10
p
u
du
16
=
1
16
_
2
3
u
3
2
_

u=26
u=10
=
_
1
24
(26)
3
2
_

_
1
24
(10)
3
2
_
=
13
p
26 5
p
10
12

12.6 #8 Find the area of the surface which is the helicoid (or spiral ramp) with vector equation
r (u; v) = ucos vi + usin vj + vk,
where 0 u 1, 0 v .
[Solution]
We have
r
u
(u; v) = cos vi + sin vj
and
r
v
(u; v) = usin vi + ucos vj + k.
To calculate the surface, we calculate jr
u
r
v
j rst.
jr
u
r
v
j =

i j k
cos v sin v 0
usin v ucos v 1

sin vi cos vj +
_
ucos
2
v + usin
2
v
_
k

= jsin vi cos vj + ukj

=
_
(sin v)
2
+ (cos v)
2
+ (u)
2
=
p
1 + u
2
.
3
Thus, the surface area is
A(S) =
__
D
jr
u
r
v
j dA =
__
D
p
1 + u
2
dA =
_
1
0
_

0
p
1 + u
2
dvdu
=
_
1
0

p
1 + u
2
du
=
_
u
2
p
1 + u
2
+
1
2
ln
_
u +
p
1 + u
2
_
_

u=1
u=0
=
1
2

_
ln
_
p
2 + 1
_
+
p
2
_
.

12.7 #4 Evaluate the triple integral

_
1
0
_
2x
x
_
y
0
2xyzdzdydx.
[Solution]
The triple integral
_
1
0
_
2x
x
_
y
0
2xyzdzdydx =
_
1
0
_
2x
x
_
xyz
2

z=y
z=0

dydx
=
_
1
0
_
2x
x
xy
3
dydx
=
_
1
0
_
x
y
4
4

y=2x
y=x
_
dx
=
_
1
0
15
4
x
5
dx
=
15
4
x
6
6

x=1
x=0
=
15
24
=
5
8
.

12.7 #8 Evaluate the triple integral

___
E
yz cos
_
x
5
_
dV ,
where
E = f(x; y; z) j 0 x 1; 0 y x; x z 2xg .
[Solution]
4
The triple integral is
___
E
yz cos
_
x
5
_
dV =
_
1
0
_
x
0
_
2x
x
yz cos
_
x
5
_
dzdydx
=
_
1
0
_
x
0
_
y
z
2
2
cos
_
x
5
_

z=2x
z=x
_
dydx
=
_
1
0
_
x
0
_
y
4x
2
x
2
2
cos
_
x
5
_
_
dydx
=
_
1
0
_
y
2
2
3x
2
2
cos
_
x
5
_

y=x
y=0
_
dx
=
_
1
0
3
4
x
4
cos
_
x
5
_
dx
=
3
4
_
1
0
cos (u)
du
5
=
3
20
sin uj
u=1
u=0
=
3
20
sin 1.

12.7 #12 Evaluate the triple integral

___
E
xzdV , where E is the solid tetrahedron with vertices
(0; 0; 0), (0; 1; 0), (1; 1; 0), and (0; 1; 1).
[Solution]
First, we recognize (0; 0; 0), (0; 1; 0), and (1; 1; 0) all lie on the xy-plane. Thus, the solid
is bounded below by the xy-plane, which is z = 0.
Another three points, (0; 1; 0), (1; 1; 0), and (0; 1; 1) all lie on the plane y = 1. Thus,
the solid is bounded on the right by the plane y = 1.
Also, (0; 0; 0), (0; 1; 0), and (0; 1; 1) all lie on the yz-plane. Thus, the solid is bounded
on the back by the yz-plane, which is x = 0.
Finally, (0; 0; 0), (1; 1; 0), and (0; 1; 1) form a plane. We have that h1; 1; 0i h0; 0; 0i =
h1; 1; 0i and h0; 1; 1i h0; 0; 0i = h0; 1; 1i are two vectors on the plane. The cross ptoduct
h1; 1; 0ih0; 1; 1i = h1; 1; 1i is the normal vector of the plane. Thus, the solid is bounded
by the plane (x 0) (y 0) + (z 0) = 0, that is x y + z = 0.
We treat the triangle formed by (0; 0; 0), (0; 1; 0), and (1; 1; 0) as the base D of the
tetrahedron. It is bounded by the lines on the xy-plane, which are x = 0, y = 1 and
x = y. We can describe it as 0 x 1 and x y 1.
With a point (x; y; 0) in the base D, the height can be seen as z = y x. So, the range
of z is 0 z y x.
Therefore, the triple integral is
___
E
xzdV =
_
1
0
_
1
x
_
yx
0
xzdzdydx =
1
120
.

5
12.7 #14 Evaluate the triple integral
___
E
(x + 2y) dV , where E is bounded by the parabolic cylin-
der y = x
2
and the plane x = z, x = y, and z = 0.
[Solution]
The intersection points on the xy-plane of y = x
2
and x = y are (0; 0; 0) and (1; 1; 0)
(since x
2
= y = x and it implies that x = 0 or 1.) So, the base D on the xy-plane is
enclosed by y = x
2
and x = y. Thus, we can describe D as 0 x 1 and x
2
y x.
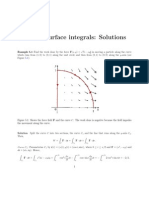
The graph of D looks like
-1.0 -0.8 -0.6 -0.4 -0.2 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0
-1
1
2
x
y
The range of z is determined by x = z and z = 0. So, we know that 0 z x since
0 x 1.
Therefore, the triple integral is
___
E
xzdV =
_
1
0
_
x
x
2
_
x
0
(x + 2y) dzdydx =
2
15
.

12.7 #18 Use a triple integral to nd the volume of the solid bounded by the cylinder y = x
2
and
the planes z = 0, z = 4, and y = 9.
[Solution]
The volume is
___
E
dV =
_
4
0
_
3
3
_
9
x
2
dydxdz = 144.

12.7 #30 Express the integral

___
E
f (x; y; z) dV as an iterated integral in six dierent ways, where
E is the solid bounded by the surface 9x
2
+ 4y
2
+ z
2
= 1.
[Solution]
.

6
12.7 #34 Write ve other iterated integrals that are equal to the iterated integral
_
1
0
_
x
2
0
_
y
0
f (x; y; z) dzdydx.
[Solution]
.

12.7 #48 Find the average value of the function f (x; y; z) = x

2
z +y
2
z over the region enclosed by
the paraboloid z = 1 x
2
y
2
and the plane z = 0.
[Solution]
The region can be described as
E =
_
(x; y; z) j 1 x 1;
p
1 x
2
y
p
1 x
2
; 0 z 1 x
2
y
2
_
.
Thus, the volume is
V (E) =
___
E
dV =
_
1
1
_
p
1x
2

p
1x
2
_
1x
2
y
2
0
dzdydx
=
_
1
1
_
p
1x
2

p
1x
2
_
1 x
2
y
2
_
dydz
=
_
1
0
_
2
0
_
1 r
2
_
rddr
=
_
1
0
2
_
r r
3
_
dr
=

2
.
The triple integral is
___
E
f (x; y; z) dV =
_
1
1
_
p
1x
2

p
1x
2
_
1x
2
y
2
0
_
x
2
z + y
2
z
_
dzdydx
=
_
1
1
_
p
1x
2

p
1x
2
_
x
2
+ y
2
_
(1 x
2
y
2
)
2
2
dydz
=
_
1
0
_
2
0
_
r
2
_
(1 r
2
)
2
2
rddr
=
_
1
0
r
3
_
1 r
2
_
2
dr
=

24
.
The average value is
f
ave
=
1
V (E)
___
E
f (x; y; z) dV =

24

2
=
1
12
.