Beruflich Dokumente
Kultur Dokumente
Lie Algebras and Lie Groups
Hochgeladen von
Mani PillaiCopyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Lie Algebras and Lie Groups
Hochgeladen von
Mani PillaiCopyright:
Verfügbare Formate
A Lie Algebras and Lie Groups" Basic Notions
A Lie algebra A is a linear space over some field F, say, for instance, the field of real numbers R or of complex numbers C, together with a binary operation [.,-], which maps pair of elelnents in A into all elelnent in A:
[., .]: (h,.9) c A A
, [h,.q] E .4.
(A.1)
It is called the Lie bracket and satisfies the following properties: 9 bilinearity:
[~h + Vk, ~] = ~[h, ~] + V[k, ~],
for all a, b C F and h, k,g E A; 9 anticommutativity:
[h, ~g + vk] = ~[h, g] + bib, k],
(A.2)
[h,.q] = -[.q, hi,
for all h, g r A; 9 Jacobi identity:
(A.3)
[h, [k, g]] + [k, [9, h]l + [~, [h, k] = o.
for all h, k, g E A. It is evident that in general the Lie bracket is not associative, i.e.
(A.4)
[h, [k, g]] r [[h, k], g],
(A.5)
the associative law being replaced by the Jacobi identity. The dimension of A is, of course, determined by the cardinality of the basis set {hj }j, which spans the underlying linear space. As a concrete example of a Lie algebra, we may mention that the Euclidean space R 3 becomes a three-dimensional Lie algebra with the Lie bracket taken as the cross product of vectors. Also, any associative algebra, with associative product f g (here simply denoted by justaposition), becomes a Lie algebra under the definition of the Lie bracket as the commutator, also called Lie product, of elements in the algebra:
{h, g] = h~ - gh. (A.6)
520
Linear Ray and Wave Optics in Phase 5pace
In a sense the c o m n m t a t o r is a measure of how n o n - c o m m u t a t i v e the algebra is. The algebra of invertible real square matrices is m a d e into a Lie algebra under the. Lie t)rodu('t (A.6), involving the familiar row-by-col~mnl multiplication of ma.triccs. Besi(tes, in the text it is seen that the algebra of the 2D illhomogelu;O~lS linear t)olynonfials (witll rest)cot to a,(tr a.cquircs a Lie a.lget)ra s t n u : t u r c lul(ter tilt; Poissoll bra,(:ket ot)eratio~l, as sinlilarly (toes the algel)ra ~f 21) l~on~ogelm~n~s (t~a,r l)~)lyll~)~fials. A h,omomo't7~h, ism a 1)(:t,w(:(:ll l,w() l.ie a,lg;el~ra,s A m u l / 3 ()v(:r t,l~(: sanle ti(:l(t /~':
a:A , B (A.7)
(letixu~s a, li~('a,r ~lm,l)t>i~g ~f A i~t() B, s~u:t~ tlm,t tl~e I.ie Iwa,t'ket i~ B ~f illm,ge(t elellltUltS ()f ~4 is ta,ktu~ I,() tlw illm,g('. ()f tile l.ie lwa~:ket ill A ()f 1,11e ()rigina,1 (~lelliell|,S; l~m~l('.ly:
[~(h), ~(g)l = ~([h, g])
v h, g e ,4.
(A.S)
If slu:ll a ll()l,,()l,l(~I't)llisll, is ()ll('~-t()-()ll(; (()r, .fitit/r s() tlmt tll(' ilw(;rs(; l~m.t)t)illg exist,s, it, is <:alh;(l a,n isomo't'phism. Ft)r all t)ra,t:tir In~rl)t)ses, is(ml()l'lflfi(: l,i(; algt;twas il,l'(~ i(l(;lltir A s'u,ba,ltl~'bra ,5 i~ .,4 is a, li~ear s~fl)Sl)a,(:e ()f A, wl~i(J~ is (:h)s(:(l ~ ( h ; r Lie lwa~:k(;t ()f ('~l(;~(;~l,s ()f ,5 witl~ (;l(;l~(;~t,s ()f $:
IS, Sl c s.
(A.0)
All ideal ill A is a lill(;a.r slfl)sl)ar J ()f A, wtfit:h is (:l()s(;(l llll(l(;r Lie |)ra(:ket ~f ~;h;lllellts ~)f J witll elellmIlt.s ~)f A:
[j, .4] c J .
(A.IO)
The dcT"ived series is reI)resente(t t)y the se(tuen(:e of sulm.lgebras ill A rec11rsively ot)ta,ilm(t Ulltler Lie 1)ra,(:ket a,t tim same level ()f (:ollnlnltal,i(m:
A D [A,A] D [[A, A], [A, A]I D IlIA, A], [A, A]], [[A, A], [A, A]]] D ....
(A.11)
Corr('~st)(nl(tingly, th(; lowe'l" cent'ml series is intended as the sequence of sllba.lgcl)ras in A obtained under rct)cate(t (right) Lie bracket with A itself:
A ~ [A, A] D [A, [A, A]] ~ [A, [A,, [A, A]]] D ....
(A.12)
A Lie algebra A is said abclian if [A, A] = 0; is said solvable if at a certain level of c o n u n u t a t i o n tile derived series terminates; and is said nilpotent if the lower central series b e c o m e s zero eventually. The Heisenberg-Weyl algebra {~, ~, I} yields a significative example of a nilpotent algebra.
A
Appendix
521
Also, a Lie algebra A is simple if it contains no nonzero ideals, whilst it is semi-simple if it contains no nonzero abelian ideals. A simple Lie algebra is semi-simple. It turns out that semi-simple Lie algebras are the direct sum of simple (non abelian) Lie algebras. A Lie group ~ combines the continuous structure of a differentiable manifold with the basic properties of groups. A group is a set of eleinents in which it is defined a binary operation (the group multiplication), which maps any two elements in G into an clement in G as well, and satisfies the properties: 9 associativity: H.(G.K)=(H.G).K (A. 13) for all H, G, K E {7; 9 existence of identity: 3 IEG 9 I .H-H (A.14)
for a l l H EG;
9 existence of unique inverse:
3 H -1 E ~} 9 H - 1 - H H - H -1 - I. (A.15)
fl)r every H C G. A familiar example is the group 7),. of all p e r m u t a t i o n s of n objects, which consists of n! operations. Also, the collection of rotations of the circle in a plane through multiples of a given angle tg, say t9 - 2~ with respect to a fixed n ~ point, constitutes a group Inade of n distinct operations. In order that G be a Lie group, its group operation must be consistent with the continuous structure of the underlying manifold, and so it must diffcrcntiable as well. This na'/vely means t h a t if H and G in G multiply to W - H - G in ~, then the group operation takes any elements J and K , respectively drawn from a neighborhood of H and a neighborhood of G, to the group element Y in a neighborhood of W. As a simple example of Lie groups, we may mention that the set of real numbers, excluding 07 forms a Lie group with respect to the familiar multiplication of numbers. The set of translations of a straight line with respect to a reference point also constitutes a Lie group, each element of which being individualizable (i.e. parameterizable) by a real number (which specifies the shift from the identity). Also, the ensemble of rotations of the circle with respect to a fixed point by an angle ~9, allowed to range continuously through the interval 0 <_ g _< 27r, generates a Lie group, whose elements can be parameterized just by the continuous angle g. It is seen in the text t h a t the group of the unimodular 2 x 2 real matrices (under the ordinary multiplication of matrices) forms a Lie group, and each matrix in it is parameterized by three real numbers, which
522
Linear Ray and Wave Optics in Phase Space
can be (tifferently interprete(1 a(:cording to the a d o p t e d (tec()mt)osition. Ano t h e r e x a m p l e is the g r o u p GL(~t) of n x n invertible m a t r i c e s , or tl~e relevant sut)gro~H) O(n) of o r t h o g ( m a l matrices. 1R.()~ghly st)caking, Lie a.lget)ras ext)(mentiate to Lie gr(nq)s. M()re t)re(:isely, the t a n g e ~ t st)a<'e at the i(hmtity of a Lie gr(n~t) is always a Lie alget)ra. This Lie algel)ra (h;tei'nfines the h)(:al str~(:t~r(; ()f the Lie gro~lt) thr(n~gh the ext)()nential nm.I). (~,()~si(t('.ri~g, f()r ill~strative tn~rI)()s(;s, a. ()n(;-t)aI'a.~u;ter I,i(; gr(nq) {7, S)~l )l )( )s(: tlm.l, (;(t) r(;l)r(:selll,s a sni()()l,h (:lit'v(: in ~; l)assil~g (,l~r()~gh (,h(: g r o u p i(le~Itity, (:.g. I -: (;(()). F()r vahu:s bt ()f (,l~(: r(:al l)ara~(:(,(:r t il~li~dl,(:simally (:h)s(; t() (), (,lle (:()rr(:sl)()~uli~g (:l(:~n(;~t (;(bt) iI~ ~ (:()~(:s t() l)(: i~fi~fi(,(:simally (:]()se (,() tl~(: i(](:~tity I = (1(()), i.(:. (A.16) tllllS (;St,alflisllillg a ~llal)l)illg ()f (;l(;111(;lll,S (;'(()) ill tll(' l,i(', alg('.l)ra t() tt~(; i~ti~fitesi~m.l ge~mrat()rs G((St) ()f (,l~(; Lie gr()~q). It ix (;vi(h;~t tlm.t l,l~(; sl, r~u:t,~r(; ()f tt~(', a lg(;1)ra ix r(;fi(;('l.(:(! l()('ally i~(,() tlm.(, ()f l,l~(; gr()~ l) i~ a ~(;iglfl)()rh()()(t ()f tl~(; i(le~tity. S~q)t)()s(; ~l()w (,() l,ak(; a. fi~ii,e ~nn~d)(;r t ~ IR. ()f ('.()~n's('., ()~(; ('a~ g() i~finitesi~m,lly (:l()s(; 1,()(), 1)y l)r()l)(,rly fra('l,i()~i~g t,; s(;(, r()~gl~ly, bl - a~(l let 1,1~(; III. in(,(:g(:r ')))g() (,() infilfi(,y: '))) --+ c~. Sill(:(:, 1)y vir(,~i(: ()f (,lle ('l()s~n'(: l)r()l)erty ()f tl~(: gr()~q), f()r a~y i~(,(:g(:r '))),, [(7'(bt)]'" l)(:l()~gs (,o (,l~(: gr()~l), w(: fi~m.lly lm.ve
[(;(~t)]'" ,.~ [I + - - _ (7,' (())] '" ~ (' to,' (()) ,
Ill,
(1.17)
/,lnls esl, at)lisllillg all (:xt)()Imlltial nmt)t)i21g l,llr(mgll (,ll(; real lm.rmllel,er t ()f eh:nl(:nl,s G ' ( 0 ) in (,he Li(: alg(:l)ra (,()" finil,(:" eh:nlenl, s ()f l,h(: I,i(: gr(nq). Histori(:ally, lSe algel)ras lm.ve enlerge(t |)y (:oIlsi(h:rillg (:l(:IIl(:lll, s in Lie gTout)s infinitesimally (:h)se t() the gr()lq) i(tentity. D u e to this i n t i m a t e link l)etween Lic algc|)ras a.n(1 I, ie g r o u p s (,lu: (:haracteriza.tion ()f Lic algebras ~llent, ione(t a,t)()ve reflects in an analog(ms (:hara,cterization (or, nlore precisely, classification) of Lie groups. A r e p r e s e i l t a t i o n of a Lie g r o u p {~ on a vector spa,(:(; V is a h o m o m o r p h i s m of {~ into the g r o u p of a u t o m o r p h i s m of V (i.e. of transforma, tion of V into itself). If a tin.sis set is chosen for the vector space V, the r e p r e s e n t a t i o n can equally t)e intende(t as a. h o m o m o r p h i s m of {7 to the g r o u p GL(n), a n d a c c o r d i n g l y it t)rovides a m a t r i x r e p r e s e n t a t i o n of t h e group. In a sense, a g, oup r e t ) r e s e n t a t i o n Inay yieht a d e s c r i p t i o n of a g r o u p in t e r m s of m o r e "visible" ot)jects.
Das könnte Ihnen auch gefallen
- Introduction to Differential Galois TheoryDokument19 SeitenIntroduction to Differential Galois TheoryAriel BorgesNoch keine Bewertungen
- Inhomogeneous: SL (N, C)Dokument9 SeitenInhomogeneous: SL (N, C)Anonymous FigYuONxuuNoch keine Bewertungen
- Methods of Constructing Functions in Involution (4s)Dokument5 SeitenMethods of Constructing Functions in Involution (4s)Adriano AraujoNoch keine Bewertungen
- Normal Form of A Hopf Bifurcation With Noise: L LX, Rat, 71Dokument6 SeitenNormal Form of A Hopf Bifurcation With Noise: L LX, Rat, 71happelNoch keine Bewertungen
- The Trace Formula For Reductive 'Groups : JamesDokument41 SeitenThe Trace Formula For Reductive 'Groups : JamesJonel PagalilauanNoch keine Bewertungen
- The Zeros of Hankel FunctionsDokument13 SeitenThe Zeros of Hankel FunctionsMelike ErdoğanNoch keine Bewertungen
- Discrete Series of GLn Over a Finite Field. (AM-81), Volume 81Von EverandDiscrete Series of GLn Over a Finite Field. (AM-81), Volume 81Noch keine Bewertungen
- Group Theoretical Quantum Tomography: G. Cassinelli, G.M. D'Ariano, E. de Vito, and A. LevreroDokument13 SeitenGroup Theoretical Quantum Tomography: G. Cassinelli, G.M. D'Ariano, E. de Vito, and A. LevreroJL ArceNoch keine Bewertungen
- The Gr6bner Fan of An IdealDokument26 SeitenThe Gr6bner Fan of An IdealMinh TuấnNoch keine Bewertungen
- PJM v52 n2 p26 SDokument21 SeitenPJM v52 n2 p26 Sajitkumar1Noch keine Bewertungen
- Exposition of Polya's Enumeration TheoremDokument17 SeitenExposition of Polya's Enumeration TheoremEugene QuahNoch keine Bewertungen
- Bocherer-Kohnen-1993-Estimates of Fourier Coefficients of Siegel Cusp FormsDokument19 SeitenBocherer-Kohnen-1993-Estimates of Fourier Coefficients of Siegel Cusp FormsTamilselviNoch keine Bewertungen
- An Extension of Buchberger's AlgorithmDokument10 SeitenAn Extension of Buchberger's AlgorithmAnonymous Tph9x741Noch keine Bewertungen
- Pacific Journal of Mathematics: Reproducing Kernels and Operators With A Cyclic Vector. IDokument21 SeitenPacific Journal of Mathematics: Reproducing Kernels and Operators With A Cyclic Vector. IKate Sai kishoreNoch keine Bewertungen
- Orthogonal Wavelets With Compact Support On Locally Compact Abelian GroupsDokument28 SeitenOrthogonal Wavelets With Compact Support On Locally Compact Abelian GroupsukoszapavlinjeNoch keine Bewertungen
- 1 s2.0 S0747717188800051 MainDokument28 Seiten1 s2.0 S0747717188800051 Maincreatorb2003Noch keine Bewertungen
- NONLOCAL BRS COUNTERTERMS IN A PHYSICAL GAUGE Leibrandt NyeoDokument7 SeitenNONLOCAL BRS COUNTERTERMS IN A PHYSICAL GAUGE Leibrandt NyeomaurodiloretoNoch keine Bewertungen
- A Model (, Hidden-Variable, Theory For Hydrogen.: (X, T) FDX' .D - (.Dokument7 SeitenA Model (, Hidden-Variable, Theory For Hydrogen.: (X, T) FDX' .D - (.Kokipro KokiproNoch keine Bewertungen
- The Value of The Ramsey Number R (3,8)Dokument7 SeitenThe Value of The Ramsey Number R (3,8)Cristian BenavidesNoch keine Bewertungen
- The Selberg Trace Formula For Groups Without Eisenstein SeriesDokument28 SeitenThe Selberg Trace Formula For Groups Without Eisenstein SeriesPaul RingsethNoch keine Bewertungen
- 6D - The Wigner Distribution Function Analytical EvaluationDokument70 Seiten6D - The Wigner Distribution Function Analytical EvaluationMani PillaiNoch keine Bewertungen
- State Space AnalysisDokument26 SeitenState Space AnalysisWilson TanNoch keine Bewertungen
- A Semi-Implicit Mid-Point Rule For Stiff Systems of Ordinary Differential EquationsDokument26 SeitenA Semi-Implicit Mid-Point Rule For Stiff Systems of Ordinary Differential EquationsKami JaraNoch keine Bewertungen
- Continuous Wavelet Transform and Continuous Multiscale AnalysisDokument18 SeitenContinuous Wavelet Transform and Continuous Multiscale Analysissarita yadavNoch keine Bewertungen
- 1969 04erdosDokument9 Seiten1969 04erdosvahidmesic45Noch keine Bewertungen
- MP (7r) Special: ............. OperatorDokument35 SeitenMP (7r) Special: ............. OperatorJonel PagalilauanNoch keine Bewertungen
- NCM Annual Foundational School Algebra Exercise Set 1Dokument2 SeitenNCM Annual Foundational School Algebra Exercise Set 1Chiranjib ChoudhuryNoch keine Bewertungen
- Time Dependent DFT PRL PDFDokument4 SeitenTime Dependent DFT PRL PDFGokaran ShuklaNoch keine Bewertungen
- 1 s2.0 0024379586902387 MainDokument13 Seiten1 s2.0 0024379586902387 Mainwalid badrNoch keine Bewertungen
- BF02189684Dokument13 SeitenBF02189684Atharv NadkarniNoch keine Bewertungen
- BF03042214Dokument12 SeitenBF03042214Julio Cesar Jaramillo QuicenoNoch keine Bewertungen
- Dealfaro 1976Dokument44 SeitenDealfaro 1976Víctor AndrésNoch keine Bewertungen
- The Trace Formula in Invariant Form: Annals of 114 (1981), 1-74Dokument74 SeitenThe Trace Formula in Invariant Form: Annals of 114 (1981), 1-74Jonel PagalilauanNoch keine Bewertungen
- A Note On Total DominationDokument7 SeitenA Note On Total DominationRosyid Asy-syifaNoch keine Bewertungen
- Dirac Combs CórdobaDokument6 SeitenDirac Combs CórdobaTest oneNoch keine Bewertungen
- 5vector FunctionDokument24 Seiten5vector FunctionNur HannaNoch keine Bewertungen
- (Lecture Notes in Mathematics 302) Michel Demazure (Auth.) - Lectures On P-Divisible Groups-Springer-Verlag Berlin Heidelberg (1972)Dokument103 Seiten(Lecture Notes in Mathematics 302) Michel Demazure (Auth.) - Lectures On P-Divisible Groups-Springer-Verlag Berlin Heidelberg (1972)陈仡韬Noch keine Bewertungen
- Fuzzy Calculus BasicsDokument13 SeitenFuzzy Calculus BasicsYuri IvanovichNoch keine Bewertungen
- SQM Problem Set 1: Groups, Representations and Their ApplicationsDokument8 SeitenSQM Problem Set 1: Groups, Representations and Their ApplicationsPhilip RuijtenNoch keine Bewertungen
- Generalized Laurent Polynomial Rings As Quantum Projective 3-SpacesDokument15 SeitenGeneralized Laurent Polynomial Rings As Quantum Projective 3-Spacesjohn_k7408Noch keine Bewertungen
- Filliman 1990Dokument18 SeitenFilliman 1990epidendrum2Noch keine Bewertungen
- 33 Geometry of SelfadjointDokument27 Seiten33 Geometry of SelfadjointGustavo CorachNoch keine Bewertungen
- Itô's Stochastic Calculus and Its ApplicationsDokument61 SeitenItô's Stochastic Calculus and Its Applicationskim haksongNoch keine Bewertungen
- Lie AsdfasfdasfdDokument83 SeitenLie Asdfasfdasfdnirb1123Noch keine Bewertungen
- Galois Groups For Polynomials Related To Quadratic Map IteratesDokument39 SeitenGalois Groups For Polynomials Related To Quadratic Map IteratesJose UgarteNoch keine Bewertungen
- Note Partitioning Permutations Into Increasing and DecreasingDokument7 SeitenNote Partitioning Permutations Into Increasing and DecreasingQuocNoch keine Bewertungen
- Theodorus Spiral - GeometriaDokument13 SeitenTheodorus Spiral - GeometriaarantheoNoch keine Bewertungen
- Galois Symmetries in CFTDokument6 SeitenGalois Symmetries in CFTalexNoch keine Bewertungen
- WongDokument6 SeitenWongAlvaro Rafael MartínezNoch keine Bewertungen
- 1 s2.0 0304397586900290 MainDokument21 Seiten1 s2.0 0304397586900290 MainLe CaméléonNoch keine Bewertungen
- Convolution Quadrature and Discretized Operational Calculus. IDokument17 SeitenConvolution Quadrature and Discretized Operational Calculus. Irezza ruzuqiNoch keine Bewertungen
- 443 Bit BoundaryDokument5 Seiten443 Bit BoundarySaint-CyrNoch keine Bewertungen
- Lee Brekke Et Al - Knots and Links of Nonabelian StringDokument17 SeitenLee Brekke Et Al - Knots and Links of Nonabelian StringPomac232Noch keine Bewertungen
- Contra Pairwise Continuity in Bitopological Spaces: Archana PawarDokument15 SeitenContra Pairwise Continuity in Bitopological Spaces: Archana PawarinventionjournalsNoch keine Bewertungen
- Rectifying Curves in The Three-Dimensional Hyperbolic Space: Pascual Lucas and Jos e Antonio Ortega-Yag UesDokument16 SeitenRectifying Curves in The Three-Dimensional Hyperbolic Space: Pascual Lucas and Jos e Antonio Ortega-Yag UesJuan Antonio VeraNoch keine Bewertungen
- The Second Bounded Cohomology of Word-Hyperbolic Groups: PergamonDokument15 SeitenThe Second Bounded Cohomology of Word-Hyperbolic Groups: PergamonGregNoch keine Bewertungen
- A Short Introduction To Quantum Symmetry: PhysicsDokument6 SeitenA Short Introduction To Quantum Symmetry: PhysicsSamuel SoaresNoch keine Bewertungen
- On Orbit Sum Values of Elements of Finite Order: Stefan Grimm 1Dokument6 SeitenOn Orbit Sum Values of Elements of Finite Order: Stefan Grimm 1Onur ÖztırpanNoch keine Bewertungen
- Reproducing Kernels and Operators With A Cyclic Vector I: e E), First Considered by LivsicDokument18 SeitenReproducing Kernels and Operators With A Cyclic Vector I: e E), First Considered by LivsicjNoch keine Bewertungen
- Commensurabilities among Lattices in PU (1,n). (AM-132), Volume 132Von EverandCommensurabilities among Lattices in PU (1,n). (AM-132), Volume 132Noch keine Bewertungen
- AppBreweryCornellNotesTemplate PDFDokument2 SeitenAppBreweryCornellNotesTemplate PDFharieswaranNoch keine Bewertungen
- AppBrewer PDFDokument2 SeitenAppBrewer PDFharieswaranNoch keine Bewertungen
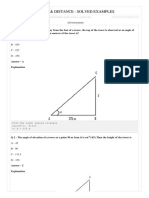
- Height & Distance - Solved ExamplesDokument6 SeitenHeight & Distance - Solved Examplesharieswaran100% (1)
- Detailed contingent bill summaryDokument1 SeiteDetailed contingent bill summaryharieswaranNoch keine Bewertungen
- Number System - PercentagesDokument1 SeiteNumber System - PercentagesharieswaranNoch keine Bewertungen
- Aptitude Height Distance PDFDokument1 SeiteAptitude Height Distance PDFharieswaranNoch keine Bewertungen
- Height & Distance - Solved ExamplesDokument6 SeitenHeight & Distance - Solved Examplesharieswaran100% (1)
- Aptitude Number System Examples PDFDokument9 SeitenAptitude Number System Examples PDFharieswaranNoch keine Bewertungen
- Aptitude Number System PDFDokument5 SeitenAptitude Number System PDFharieswaranNoch keine Bewertungen
- Aptitude Percentages ExamplesDokument6 SeitenAptitude Percentages ExamplesharieswaranNoch keine Bewertungen
- Aptitude Number System PDFDokument5 SeitenAptitude Number System PDFharieswaranNoch keine Bewertungen
- Aptitude HCF LCM ExamplesDokument7 SeitenAptitude HCF LCM ExamplesharieswaranNoch keine Bewertungen
- Aptitude Number System Examples PDFDokument9 SeitenAptitude Number System Examples PDFharieswaran100% (1)
- Aptitude HCF LCM PDFDokument1 SeiteAptitude HCF LCM PDFharieswaranNoch keine Bewertungen
- Aptitude Height DistanceDokument1 SeiteAptitude Height DistanceharieswaranNoch keine Bewertungen
- Aptitude HCF LCM ExamplesDokument7 SeitenAptitude HCF LCM ExamplesharieswaranNoch keine Bewertungen
- Contingent Bill: Annexure - ViiDokument1 SeiteContingent Bill: Annexure - ViiharieswaranNoch keine Bewertungen
- Height & Distance - Solved ExamplesDokument6 SeitenHeight & Distance - Solved Examplesharieswaran100% (1)
- Aptitude - Decimals & FractionsDokument3 SeitenAptitude - Decimals & FractionsharieswaranNoch keine Bewertungen
- Number System - DiscountsDokument1 SeiteNumber System - DiscountsharieswaranNoch keine Bewertungen
- Discounts - Solved ExamplesDokument4 SeitenDiscounts - Solved ExamplesharieswaranNoch keine Bewertungen
- Aptitude - Basic ArithmeticDokument2 SeitenAptitude - Basic ArithmeticharieswaranNoch keine Bewertungen
- Adobe After Effects Cheat Sheet: Most Commonly Needed Keyboard ShortcutsDokument2 SeitenAdobe After Effects Cheat Sheet: Most Commonly Needed Keyboard ShortcutsharieswaranNoch keine Bewertungen
- Aptitude - Decimals & Fractions Solved ExamplesDokument7 SeitenAptitude - Decimals & Fractions Solved ExamplesharieswaranNoch keine Bewertungen
- Aptitude - Averages ExamplesDokument7 SeitenAptitude - Averages ExamplesharieswaranNoch keine Bewertungen
- Aptitude - Basic Arithmetic ExamplesDokument8 SeitenAptitude - Basic Arithmetic ExamplesharieswaranNoch keine Bewertungen
- Aptitude Averages PDFDokument1 SeiteAptitude Averages PDFharieswaranNoch keine Bewertungen
- Contingent Bill PDFDokument2 SeitenContingent Bill PDFbdoranni86% (7)
- Sivagamiyin Sabatham Part3Dokument143 SeitenSivagamiyin Sabatham Part3api-19854516Noch keine Bewertungen
- Just For FunDokument1 SeiteJust For FunharieswaranNoch keine Bewertungen