1

Lecture 2: Limit, Continuity and

Differentiability

1. Limit
In engineers language, it suffices to say that
a x f
x x
=

) ( lim
0
means that f(x) can be arbitrarily
close to a when
x
is sufficiently close to 0
x

(note: x does not have to equal 0
x
).

How to find the limit of f(x)?
Two approaches: (i) Draw the function, and see what
value f(x) approaches as x-> 0
x
.
(ii) Check the value of
) (
0
x f
.

Examples:
(i). For a function f(x)=x, what is its limit at x=2?

(ii). Consider a function

=
=
=
2 .......... 8
2 ........
) (
2
x
x x
x f

Find its limit as x=2.

For the second example, the limit does not equal f(2)! So, if
possible, it is better to use the first approach to determine a limit.


2
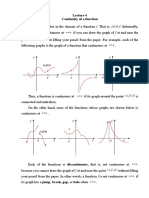
2. Continuity


Example: Which function in the first two examples is
continuous, and which is not? This can be seen clearly by
plotting the function.

3. Differentiability

If
a
h
x f h x f
h
=
+

) ( ) (
lim
0 0
0
, then we say that f(x) is
differentiable at 0
x
and write

a x f = ' ) (
0
.
Geometrically,
) (
0
x f '
means the slope of the curve of
f(x) at x= 0
x
.

Note that if f(x) is differentiable at x= 0
x
, it is also
continuous at 0
x
. The converse is not true, however
(counter-example:
x x f = ) (
).


3
The function in this counter-example can be written
explicitly as:

=
<
>
=
0. x if 0,
0, x if x, -
, x if x
x f
0 ,
) (

Consideration its differentiability at x=0. As h->0
+

(i.e., h approaches 0 from the positive side of 0 and h
is positive),
1
0
lim
0
=

h
h
h
. On the other hand, as h->0
-

(i.e., h approaches 0 from the negative side of 0 and h
is negative),

1
0
lim
0
=

+

h
h
h
.
Since
h
h
h
h
h h
0
lim
0
lim
0 0

, there does not exist

differentiation of f(x) at x=0.

In short, a function is not differentiable at x=x
0
, if
(i)
h
x f h x f
h
x f h x f
h
h
) ( ) (
lim
) ( ) (
lim
0 0
0
0 0
0
+
=
+
+

.
Geometrically, this implies that the function has a
sharp corner at this point, for example, | | ) ( x x f = has a
sharp corner at x=0 as shown below. A function has
to be smooth at a point for it to be differentiable at
this point.

4









(ii) f(x) is not continuous at x=x
0.
Being not
continuous means that there is a hole at x=x
0
. That is,
as h->0,
) (
0
h x f +
does not necessarily approach f(x
0
).
This further means the nominator in
is a finite value. However, the
denominator in this expression goes to zero.
Therefore, the limit goes to infinity, i.e., there is no
limit. Thus f(x) is not differentiable at this point.

4. Five examples
Note that for continuity, we need to show that




x
f(x)
0
5
For differentiability, we need to show that
equals a particular value.

It is observed that the absolution value of a sine
function is not greater than 1. Making use of this
condition, we have


6
Note that
)
1
sin(
h
changes its value between -1
and 1, thus not approaching a particular value as h->0.



3. Find the derivatives of the following functions at
x=6:

(a) x and (b) x
2

4. The limit of the following function at x=2:
7

=
number irrational a is x if 1, -
number, rational a is x if
x f
, 1
) (
.
Note there is no limit of this function at any point
since in any small neighborhood of x=2, we can
always find both rational and irrational numbers, the
corresponding values of f(x) are 1 and -1, respectively
and do not approach to a specific value. Therefore,
there does not exist a limit.


5.





8
How to determine the limits of some special functions?


Exercise:


Answers: (a) , (b) infinity (assume n=2), (c) 1, and (d) 1

9
Note that due to the requirement that , the
above theorem is only applicable to the cases of
0
0
and

, such
as (a),(b) and (c). Cannot be applied to other cases, such as (d)
since the requirement is violated.