THE ENERGY EQUATION

A fluid in motion is subjected to several forces, resulting in variation of fluid acceleration and the
energies associated with flow. Forces acting on a fluid mass in motion can be broadly categorised
into (i) body or volume forces that are proportional to the volume of the fluid such as self weight,
centrifugal force etc, (ii) surface forces that are proportional to the surface area such as pressure
force, shear or tangential force, force due to compressibility of the fluid, force due to turbulence etc
and (iii) line forces that are proportional to length such as surface tension. The dynamics of fluid
is governed by Newtons second law of motion that states that the resultant force on any fluid
element is equal to the product of the mass and the fluid acceleration. The acceleration vector and
the resultant force vector have the same direction. In mathematical form, this can be written as
a F m =

, where

Fis the vector of resultant forces acting on a fluid element of mass mand
a is the acceleration vector. In the study of fluids in motion, in many cases, the forces per unit
volume of the element f are required to be determined and this can be evaluated as a f = .

In general, the forces that may influence the motion of a fluid includes (i) gravity force
g
F - due to
the self weight of the fluid = g m , where g is the acceleration due to gravity, (ii) pressure force
p
F - due to a pressure gradient existing between two points in the direction of flow, (iii) viscous
force
v
F - due to the viscosity of the fluid (exists in the case of all real fluids), (iv) force due to
turbulence in the flow
t
F - the continuous moment exchange in the fluid due motion of fluid
particles results in the development of additional stresses called Reynolds stresses (v) force due to
compressibility of the fluid
e
F - due to the elastic properties of the fluid and (vi) surface tension
force
s
F due to the cohesive property of the fluid mass. If the motion of a fluid mass is influenced
by all the above forces, then the equation of motion in a typical coordinate direction, say i , can be
written as
s e t v p g i i
F F F F F F a m F + + + + + = =

In many problems involving fluid flow, the surface tension forces and forces due to fluid
compressibility are not significant and hence these may be neglected. The resulting equations of
motion are called Reynolds equations of motion and these are used in the analysis of turbulent
flows. In the case of laminar or viscous flows, the forces due to turbulence are also not significant
and this yields the Navier-Stokes equations. If the viscous forces are also insignificant, then only
gravity and pressure forces need to be considered while formulating the equations of motion. The
resulting equations are called Eulers equations of motion.
Eulers Equations of Motion and Bernoullis Equation
The equation of motion for a frictionless fluid can be derived by considering all the forces which act on a
fluid element. In the case of Eulers equations of motion, only two forces - surface forces (which act on
various surfaces of the fluid element (pressure forces) and body forces (gravitational forces fluid weight)
are taken into account.

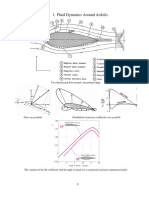
Consider a point P ( ) z y x , , in a flowing mass of fluid at which the velocities in the z and y x , ,
directions are w and v u , , respectively; the mass density of the fluid is and the pressure intensity is
p . Fig. shows an element of fluid of size z y x o o o at P.
Net pressure force acting on the element in the x direction=
(

If X is the body force/unit mass in the x -direction, the net body force in the x -direction =
Surface forces + body forces = mass x acceleration

where,
Dt
Du
is the total derivative.
x
p
X
c
c

1
=
Dt
Du
is the equation of motion in the x -direction
Similarly we have in the y -direction

and

in the z - direction, where Z and Y are body forces/unit mass in the z and y -directions respectively.
The accelerations in the z and y x , , directions can be written as .

With the x and y axes horizontal and the z axis vertical, X = Y
=
0 and Z = - g =

()
Assuming the motion to be irrotational, we have
0
2
1
0
2
1
0
2
1
=
|
.
|

\
|
c
c

c
c
=
= |
.
|

\
|
c
c

c
c
=
= |
.
|

\
|
c
c

c
c
=
x
w
z
u
z
v
y
w
y
u
x
v
y
x
z
e
e
e

Therefore,

From the definition of velocity potential,

The equations of motion can now be written as

()

Further,

Also, assuming fluid density to be uniform,
|
|
.
|

\
|
c
c
=
|
.
|

\
|
c
c
|
|
.
|

\
|
c
c
=
|
.
|

\
|
c
c

p
z z
p
and
p
x x
p 1 1

Hence, ( ) 0
2
1
2 2 2
= |
.
|

\
|
+ + + +
c
c

c
c

| p
w v u
t x

( ) 0
2
1
2 2 2
= |
.
|

\
|
+ + + +
c
c

c
c

| p
w v u
t y

and
( ) 0
2
1
2 2 2
= |
.
|

\
|
+ + + + +
c
c

c
c
gz
p
w v u
t z
|

Integrating these equations we get,
( )

| p
w v u
t
+ + + +
c
c

2 2 2
2
1
( ) t z y F , ,
1
=
( )

| p
w v u
t
+ + + +
c
c

2 2 2
2
1
( ) t z x F , ,
2
=
and ( ) gz
p
w v u
t
+ + + + +
c
c

|
2 2 2
2
1
( ) t y x F , ,
3
=
From the above, = gz ( ) t y x F , ,
3

- ( ) t z y F , ,
1

and = gz ( ) t y x F , ,
3

- ( ) t z x F , ,
2

Since, g is not a function of x and y ,
3
F is a function of time alone. Hence,
( ) ( ) gz t F t z y F =
3 1
, , and ( ) ( ) gz t F t z x F =
3 2
, ,
Hence, the above equations can be reduced to a single equation as
( )

| p
w v u
t
+ + + +
c
c

2 2 2
2
1
gz + = ( ) t F
3

For steady flow, ( ) = =
c
c
t F and
t
3
0
|
constant. Hence, the above equation becomes

2
v

This is the steady state Bernoullis equation.

In general,
( )

| p
w v u
t
+ + + +
c
c

2 2 2
2
1
gz + =
This is the integrated equation of motion (irrotational flow, fluid density is invariant).
Substituting, ( )
2 2 2 2
V w v u = + + , we get,

This is general equation of motion. For steady flow, this becomes,

This is the Bernoullis equation applicable for steady irrotational flow of an incompressible fluid. If the fluid
is compressible, the corresponding equation will be
constant z g
V dp
= + +
}
2
2

Each term in the above equations represent energy possessed by the fluid per unit mass of the fluid.
Bernoullis equation can also be written as

Each term in the above equation represents energy possessed by the fluid per unit weight of the fluid. This
has dimensions of length and is called head. The term

is called pressure head or static head,

is called
velocity head or kinetic head, and is called datum head or potential head. The sum of these three heads is
called total head (total energy per unit weight of the fluid. The sum of the pressure head and potential
head,

is called piezometric head.

The Bernoulls equation applied between any two points in a steady, irrotational flow of an incompressible
fluid yields,
2
2
2 2
1
2
1 1
2 2
z
g
V p
z
g
V p
+ + = + +


However, this is true only in the case of ideal fluids. In real fluids, there will be some loss of energy as flow
occurs and hence the above equation may be modified as
L
h z
g
V p
z
g
V p
+ + + = + +
2
2
2 2
1
2
1 1
2 2

where,
L
h = energy (head) loss between sections 1 and 2.


Newton's Second Law of Motion
As a fluid particle moves from one location to another, it usually experiences acceleration or
deceleration. According to Newton's Second Law of Motion, the net force on the fluid particle
under consideration is given by F=ma. Let us consider the motion of inviscid fluids (viscosity is
zero --> thermal conductivity of the fluid=0, there can be no heat transfer except by radiation). In
practice, there are no inviscid fluids. However in many flow situations, the viscous effects are
several orders of magnitude smaller compared to forces due to gravity or pressure differences
(normally in the case of flow of water, flow of gases etc). Assuming that the fluid motion is
governed by pressure and gravity forces only and examining Newton's Second Law of Motion as it
applies to a fluid panicle we have: (Net pressure force on a particle) + (Net gravity force on the
particle) = (Particle mass) x (particle acceleration). To apply Newton's Second Law to a fluid (or
any other object), we must define an appropriate coordinate system in which fluid motion is to be
described. In general, the motion will be 3D and unsteady. Hence three space coordinates and time
are needed to describe it (cart esi an or rectangular coordinate system ( ) z y x , , or cylindrical
polar coordinate system ( ) z r , ,u ). The specific flow geometry determines which of the above is
the most appropriate.

Let us consider 2D motion like that confined to the z x plane. The motion of each particle is
described in terms of its velocity vector V which is defined as the time rate of change of position of
the fluid particle. This is a vector with magnitude equal to the speed V given by V = |V| and
direction. As the particle moves about, it follows a particular path. The shape of this path is
governed by the velocity of the fluid particle. The location of the particle along the path is a
function of where the particle started at the initial time and its velocity along the path. If the flow is
steady, each successive particle that passes through a given path will follow the same path and this
is fixed in the z x plane. For steady flows, each particle slides along its path, its velocity vector
being tangential to the path. The lines that are tangent to the velocity vectors throughout the flow
field are called streamlines. We can use a coordinate system based on streamlines to describe the
fluid motion. The particle motion can be described in terms of its distance ( ) t s s = along the
streamline from some convenient origin and the local radius of curvature of the streamline
( ) s R R = . The distance along the streamline is related to the particle's speed as
dt
ds
V = and the
radius of curvature is related to the shape of the streamline. In addition to the coordinate along the
streamline s , the coordinate normal to the stream line n is also useful.


To apply Newton's second law of motion to a particle flowing along a streamline, the particle
acceleration has to be written in terms of the streamline coordinates. Acceleration is the time rate of
change of velocity of the particle, i.e.
dt
dV
a = . For a 2D flow in the z x plane, it has two
components - one along the stream line
s
a (stream-wise acceleration) and the other normal to the
stream line
n
a (normal acceleration). The stream-wise acceleration results from the fact that speed
of the particle may vary along the stream line. The components of acceleration in the s direction is
given by
|
.
|

\
|
c
c
=
c
c
= =
s
V
V
dt
ds
s
V
dt
dV
a
s

The normal component of acceleration (in the ndirection) is the centrifugal acceleration (since the
particle does not flow in a straight line), given by
R
V
a
n
2
= , where Ris the radius of curvature of
the path. Both V and Rmay vary along a streamline. In general, there is acceleration along the
streamline since the speed of the particle changes along its path and acceleration normal to the
stream line since the particle does not flow in a straight line. To produce this acceleration, there
must be a net non zero force on the fluid particle.

a F m = along a streamline
Consider the free body diagram of a small fluid particle of size s o x n o in the plane of the Fig. and
y o normal to the plane of the Fig. In this case, the important forces are assumed to be pressure and
gravity forces. Viscous forces and surface tension effects are assumed to be negligible. The
acceleration due to gravity g is constant and acts vertically in the negative z direction at an angle
u to the normal to the streamline.


Unit vectors along and normal to the streamlines are denoted by
^
s and
^
nrespectively. For steady
flow, the component of Newton's second law along the streamline direction s can be written as
s
V
V
s
V
V m a m F
s s
c
c
=
c
c
= =

o o o o ------- (1)

s
F o is the sum of the s components of all forces acting on the particle of mass = o om and
s
V
V
c
c
is the acceleration in the s direction. o = s o x n o x y o . Equation 1 is valid for both
compressible and incompressible fluids. The gravity force on the particle = o oW , where
g = is the specific weight of the fluid. Its component in the direction of the streamline is
u o u o o sin sin = = W W
s
............................. (2)
If the streamline is horizontal, 0 = u and there is no component of the particle weight along the
streamline to contribute to its acceleration in that direction.

x
z
Pressure is not constant through a stationary fluid because of the fluid weight. In general, for steady
flow, ( ) n s p p , = . Let the pressure at the centre of the fluid particle be p . Then its average value
on the two end faces that are perpendicular to the streamline are
s
p p o + and
s
p p o , where
s
p o
can be approximated as
2
s
s
p
p
s
o
o
c
c
=
(Assuming the particle to be small, we use only one term in the Taylor series expansion for the
pressure field). If
ps
F o is the net pressure force on the particle in the streamline direction, then
( ) ( ) ( )
c
c
=
c
c
= + = o o o o o o o o o o o
s
p
y n s
s
p
y n p p y n p p F
s s ps
................... (3)
The actual level of pressure p is not important. The non zero pressure gradient
^ ^
n s
s
p
s
p
p
c
c
+
c
c
= V
produces a net pressure force on the particle. Viscous forces are zero since the fluid is assumed to
be inviscid. Therefore, the net force acting in the streamline direction on the particle is given by

|
.
|

\
|
c
c
= + =

o 0 o o o
s
p
F W F
ps s s
sin --------------- (4)
Combining (1) and (4), we get the equation of motion along the stream line as
s
p
c
c
0 sin =
s
V
V
c
c
..................................... (5)
The physical interpretation of eqn. (5) is as follows: A change in fluid particle speed is
accomplished by the appropriate combination of pressure gradient and the particle weight along the
streamline. For fluid static situations, this balance is such that there is no change in the particle
speed - the RHS of (5) =0 and the particle remains stationary. In a flowing fluid, these forces do not
necessarily balance - the force unbalance provides the appropriate acceleration and hence, particle
motion.
Along a stream line,
ds
dz
= u sin . Also,
( )
ds
V d
ds
dV
V
2
2
1
= . Further, along a streamline, the
value of nis a constant ( ) 0 = dn and hence . ds
s
p
dn
n
p
ds
s
p
dp
c
c
=
c
c
+
c
c
= Along the streamline,
ds
dp
s
p
=
c
c
. Substituting these in (5), we get,
( )
ds
V d
ds
dp
ds
dz
2
2
1
= and this can be simplified
as
( ) streamline a along dz V d dp 0
2
1
2
= + +

This can be integrated to give
streamline a along C t cons gz V
dp
tan
2
1
2
= + +
}


CC is the constant of integration which can be determined if the conditions at some point on the
streamline is known. In general, the pressure term cannot be integrated, because the. density may not be
constant. To integrate, we should know how density varies with pressure. (For a perfect gas,
T R p = where = R Universal Gas Constant. For steady flow of an inviscid, incompressible
fluid this becomes,
streamline a along t cons z V p tan
2
1
2
= + +
This is the celebrated Bernoulli's equation (a very poverful tool in Fluid Mechanics. Daniel
Bernoulli 1738 > published Hydrodynamics - an eqnvalent of this famous equation
appeared first. In general, this equation is valid for both planar and nonplanar (3D) flows, provided
it is applied along a stream line.

F = ma Normal to the Streamline
In many flows, the streamlines are relatively straight, the flow is essentially 1D and variations in
parameters across streamlines in the normal direction can be neglected compared to the variations along
the streamline. However in many other situations, valuable information can be obtained from
considering F = ma normal to the streamlines. Considering force balance of components in the normal
direction n and writing Newton's second law in this direction, we have,
R
V
R
V m
F
n
2 2

= =

o o
o ................................ (6)

n
F o is the sum of the ncomponents of all forces acting on the particle of mass = o om . It
is assumed that the flow is steady with a normal acceleration
R
V
a
n
2
= , where R = local radius of
curvature of the stream lines. (
n
a is produced by change in direction of the particles as it moves along a
curved path). Assuming that the only forces of importance are pressure and gravity, the component
of gravity force in the normal direction is
u o u o o cos cos = = W W
n

If the pressure at the centre of the particle is p , then its values on the top and bottom of the particle
are
n
p p o + and
n
p p o , where
n
p o can be approximated as
2
n
n
p
p
n
o
o
c
c
= ................................. (7)
If
pn
F o is the net pressure force on the particle in the normal direction, then
( ) ( ) ( )
c
c
=
c
c
= + = o o o o o o o o o o o
n
p
y n s
n
p
y s p p y s p p F
n n pn
................... (8)
Therefore, the net force acting in the normal direction on the particle is given by

|
.
|

\
|
c
c
= + =

o 0 o o o
n
p
F W F
pn n n
cos --------------- (9)
Combining (6) and (9), we get the equation of motion across the stream line as
n
p
c
c
0 cos =
R
V
2

..................................... (10)
But,
dn
dz
= u cos and hence,
n
p
dn
dz
c
c
=
R
V
2

..................................... (11)
The physical interpretation of the above equation is that a change in the direction of flow of a fluid
particle (i. e., a curved path < R is accomplished by the appropriate combination of pressure
gradient and particle weight normal to the streamline. Larger speed or density or smaller Rrequires
a large force unbalance to produce the motion, eg: - if gravity is neglected (as normally done for the
flow of gases) or if the flow is in a horizontal ( ) 0 =
dn
dz
plane, equation (11) becomes,
n
p
c
c
=
R
V
2

............................ (12)
This implies that pressure increases with distance away from the centre of curvature.
n
p
c
c
is
negative since
R
V
2

is positive - the positive ndirection points towards the inside of the curved
stream line. Thus, the pressure outside a tornado is larger than that near the centre of the tornado.
This pressure difference is needed to balance the centrifugal acceleration associated with the curved
streamlines of the fluid motion. Multiplying equation (11) by dn, assuming
n
p
c
c
=
dn
dp
if s is a
constant, and integrating across the stream line in the ndirection, we get,
= + +
} }
gz dn
R
V dp
2

constant across a streamline

(We should know how varies with p and how the fluid speed and radius of curvature vary with
nto perform this integration). ( ) n s V V , = and ( ) n s R R , = . For incompressible fluids,

p dp
=
}
. Therefore, for steady flow of an inviscid, incompressible fluid, the final form of
Newton's second law of motion applied across the streamlines is,
}
= + + z dn
R
V
p
2
constant across a streamline
Physical interpretation
Application of the equation F=ma along and normal to a streamline yields the following equations.
streamline a along t cons z V p tan
2
1
2
= + + ------ (13)
}
= + + z dn
R
V
p
2
constant across a streamline ....... (14)
Assumptions
Steady flow, inviscid and incompressible fluid. Violation of one or more of these assumptions is
the common cause for an incorrect match between real world and solutions obtained using the
Bernoulli equation. The Bernoulli equation was obtained by integration of the equation of motion
along the natural coordinate direction of the streamlines. To produce an acceleration, there must be
an unbalance of the resultant forces, of which only pressure and gravity forces were considered
important. The three processes involved in the flow here are mass times acceleration (
2
2
V

term), pressure (the p term) and weight ( z term). Integration of the equation of motion to derive
the Bernoulli equation corresponds to the work energy principle often used in dynamics (obtained
by integrating the equations of motion for an object). The work energy principle may be stated as
"The work done on a particle by all the forces acting on the particle = change in the kinetic energy
of that particle''. The Bernoulli equation is the mathematical statement of the above principle. As a
fluid particle moves, both gravity and pressure forces do work on the particle. The z and p terms
are related to the work done by weight and pressure forces respectively. The
2
2
V
term is
related to the kinetic energy of the particle. An alternative form of Bernoulli equation is
= + + z
g
V p
2
2

= constant on a streamline (energy/ unit weight or length units)

z related to the potential energy of the particle > elevation head

p
pressure head (height of a column of fluid that is needed to produce a pressure p )
g
V
2
2
> velocity head (vertical distance needed for the fluid to fall freely (without friction) if it is
to reach velocity V from rest). The Bernoulli equation can also be derived from the first and second
laws of thermodynamics (the energy and the entropy equations).
The Bernoulli Equation for Irrotational Flow
For incompressible, irrotational flow, the Bernoulli equation can be written as
= + + z
g
V p
2
2

constant between any two points in the flow field

(throughout the flow field - not limited to application along a streamline).
However the equation is restricted to
> Inviscid fluid
> Steady flow
> Incompressible fluid
> Irrotational flow