Beruflich Dokumente
Kultur Dokumente
Microwave Filters
Hochgeladen von
Linh TajOriginalbeschreibung:
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Microwave Filters
Hochgeladen von
Linh TajCopyright:
Verfügbare Formate
Prof. T. L.
Wu
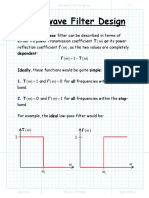
Microwave Filter Design
Chp3. Basic Concept and Theories of Filters
Prof. Tzong-Lin Wu
Department of Electrical Engineering
National Taiwan University
Prof. T. L. Wu
Transfer Functions
General Definitions
Transfer function: a mathematical description of network response characteristics.
The transfer function of a 2-port filter network is usually defined as:
where is the ripple constant, Fn() is the characteristic function, and is the
frequency variable of a lowpass prototype filter that has a cutoff frequency
for (rad/s).
For linear, time invariant networks, the transfer function may be defined as a rational
function:
where N(p) and D(p) are polynomials in a complex frequency variable p= +j. For a
lossless passive network, the neper frequency (damping coefficient) =0 and p= j.
c
= 1
c
=
Prof. T. L. Wu
Transfer Functions: Definitions
Insertion Loss
Return Loss
Phase Response
Group Delay Response
Prof. T. L. Wu
Transfer Functions:
Poles and Zeros on the Complex Plane
Complex Plane (p-plane) : (, )
The values of p at which the function becomes zero are the zeros of the function, and the values
of p at which the function becomes infinite are the singularities (usually the poles) of the function.
Therefore, the zeros of S21(p) are the roots of the numerator N (p) and the poles of S21(p) are
the roots of denominator D (p).
These poles will be the natural frequencies of the filter.
For the filter to be stable, these natural frequencies must lie in the left half of the p-plane, or on
the imaginary axis.
D(p) is a Hurwitz polynomial, i.e., its roots (or zeros) are in the inside of the left half-plane, or on
the j-axis,
the roots (or zeros) of N(p) may occur anywhere on the entire complex plane. The zeros of N (p)
are called finite-frequency transmission zeros of the filter.
Prof. T. L. Wu
Butterworth (Maximally Flat) Response
where n is the degree or the order of filter, which corresponds to the number of reactive
elements required in the lowpass prototype filter.
Maximally flat because its amplitude-squared transfer function has the maximum
number of (2n 1) zero derivatives at = 0.
Prof. T. L. Wu
Butterworth (Maximally Flat) Response
Prof. T. L. Wu
Order dependence
Prof. T. L. Wu
Chebyshev Response
Prof. T. L. Wu
Chebyshev Polynomial
The solutions are the Chebyshev polynomials of the first and second kind, respectively
Chebyshev Differential Equations
Chebyshev Polynomial of the first kind Chebyshev Polynomial of the second kind
The Chebyshev polynomials of the first kind
can be defined by the trigonometric identity
The Chebyshev polynomials of the second kind
can be defined by the trigonometric identity
Prof. T. L. Wu
Chebyshev Response
Rhodes has derived a general formula of the rational transfer function
Similar to the maximally flat case, all the transmission zeros of S21(p) are located at
infinity. Therefore, the Butterworth and Chebyshev filters dealt with so far are
sometimes referred to as all-pole filters.
The pole locations for the Chebyshev lie on an ellipse in the left half-plane.
Prof. T. L. Wu
Poles of Chebyshev Filter
Using the complex frequency s, the poles satisfy
Defining js = cos() and using the trigonometric definition of the Chebyshev polynomials yields
Solving for
The poles of the Chebyshev gain function are then
Using the properties of the trigonometric and hyperbolic functions, this may be written in explicitly complex form:
It demonstrates that the poles lie on an ellipse in s-space centered at s = 0 with a real semi-axis of length
and an imaginary semi-axis of length of
Prof. T. L. Wu
Poles of Chebyshev Filter
http://en.wikipedia.org/wiki/Chebyshev_filter
Prof. T. L. Wu
Elliptic Function Response
Prof. T. L. Wu
Elliptic Function Response
Prof. T. L. Wu
Elliptic Filter
An elliptic filter (also known as a Cauer filter, named after Wilhelm Cauer) is a signal
processing filter with equalized ripple (equiripple) behavior in both the passband and the
stopband.
The amount of ripple in each band is independently adjustable, and no other filter of equal
order can have a faster transition in gain between the passband and the stopband, for the
given values of ripple (whether the ripple is equalized or not).
As the ripple in the stopband approaches zero, the filter becomes a type I Chebyshev filter.
As the ripple in the passband approaches zero, the filter becomes a type II Chebyshev filter
and finally, as both ripple values approach zero, the filter becomes a Butterworth filter.
Prof. T. L. Wu
Elliptic Filter
The gain of a lowpass elliptic filter as a function of angular frequency is given by:
where R
n
is the nth-order elliptic rational function and
0
is the cutoff frequency
is the ripple factor
is the selectivity factor
The value of the ripple factor specifies the passband ripple,
while the combination of the ripple factor and the selectivity
factor specify the stopband ripple.
The passband of the gain therefore will vary
between 1 and
The gain of the stopband therefore will vary
between 0 and
where
Prof. T. L. Wu
Elliptic Filter
Elliptic filters are sharper than all the others, but they show ripples on the whole bandwidth
Prof. T. L. Wu
Gaussian (Maximally Flat Group-Delay) Response
1. Poor selectivity
2. BW depends on order n ?
Prof. T. L. Wu
Gaussian (Maximally Flat Group-Delay) Response
With increasing filter order n, the selectivity improves little and the insertion loss in decibels
approaches the Gaussian form
Unlike the Butterworth response, the 3 dB bandwidth of a Gaussian filter is a function of the filter
order; the higher the filter order, the wider the 3 dB bandwidth.
Advantage: A quite flat group delay in the passband
Prof. T. L. Wu
All-pass Response
The transfer function of an all-pass network is defined by
However, there will be phase shift and group delay produced by the allpass network.
In mathematics, a Hurwitz polynomial, named after Adolf Hurwitz, is a polynomial whose coefficients are positive real
numbers and whose zeros are located in the left half-plane of the complex plane, that is, the real part of every zero is
negative.
Prof. T. L. Wu
All-pass Response
If all poles and zeros of an all pass network are located along the -axis, such a network is said to
consist of C-type sections and therefore referred to as C-type all-pass network.
If the poles and zeros of the transfer function are all complex with quadrantal symmetry about the
origin of the complex plane, the resultant network is referred to as D-type all-pass network
consisting of D-type sections only.
C-type (single section)
Prof. T. L. Wu
All-pass Response
D-type (single section)
Prof. T. L. Wu
Lowpass Prototype Filters
Filter syntheses for realizing the transfer functions usually result in the so-called lowpass prototype
filters
n-pole lowpass prototype for realizing an all-pole filter response, including Butterworth, Chebyshev,
and Gaussian responses.
source resistance
source conductance
load resistance
load conductance
load conductance
load resistance
These g-values are supposed to be the inductance in henries, capacitance in farads, resistance in ohms,
and conductance in mhos.
Ladder Network
Dual
Prof. T. L. Wu
Butterworth Lowpass Prototype Filters
Prof. T. L. Wu
Chebyshev Lowpass Prototype Filters
Prof. T. L. Wu
Chebyshev Lowpass Prototype Filters
Prof. T. L. Wu
Elliptic Lowpass Prototype Filters
The series branches of parallel-resonant circuits are introduced for realizing the finite-frequency
transmission zeros
The shunt branches of series-resonant circuits are used for implementing the finite-frequency
transmission zeros
Prof. T. L. Wu
Elliptic Lowpass Prototype Filters
Unlike the Butterworth and Chebyshev lowpass prototype filters, there is no simple formula
available for determining element values of the elliptic function lowpass prototype filters.
Prof. T. L. Wu
Gaussian Lowpass Prototype Filters
It is noteworthy that the higher order (n >= 5) Gaussian filters extend the
flat group delay property into the frequency range where the insertion loss has exceeded
3 dB.
Prof. T. L. Wu
All-Pass, Lowpass Prototype Filters
By inspection
S-parameters can then be derived
Prof. T. L. Wu
All-Pass, Lowpass Prototype Filters
It can derived that
21
11 22 11 22 12 21
( )
1
1/
1/
b a
i
i
k
k
z z
S j
z z z z z z
j g
j g
p
p
+ + +
=
+
=
+
C-type
If the elements are assigned as
p. 14 in slides
Prof. T. L. Wu
All-Pass, Lowpass Prototype Filters
D-type
Similar to C-type, the elements are assigned as
Prof. T. L. Wu
FREQUENCY AND ELEMENT TRANSFORMATIONS
Frequency and impedance scaling
Lowpass Transformation
Highpass Transformation
Bandpass Transformation
Bandpass Transformation
Prof. T. L. Wu
Impedance and frequency scaling
Normalized source resistance/conductance g
0
= 1
Cutoff frequency
c
= 1
impedance scaling : define an impedance scaling factor
0
Scaled value : impedance impedance
0
L
0
L C C/
0
R
0
R G G/
0
The impedance scaling will remove the g
0
= 1 normalization and adjust the filter to work for any value of
the source impedance denoted by Z0. This scaling will has no effect on the response shape.
Resistive element transformation for the generic term g for the lowpass prototype elements in the
element transformation
Prof. T. L. Wu
Impedance and frequency scaling
Frequency scaling :
scaled values :
Impedance and Frequency scaling :
scaled values :
( )
2
2
21 21
c c
c c
S j S j
| | | |
= =
| |
\ \
c c
c c
j L j L L L
| | | |
= =
| |
\ \
1 1 c
c c
c
C C
j C
j C
| |
= =
|
| |
\
|
\
Prof. T. L. Wu
Lowpass Transformation
Example:
Prof. T. L. Wu
Highpass Transformation
0 , ,
c
c c
c
c c
=
c -c
0
0
0
1 1 1
c c c c
j L L
C C C
j j
| |
= = =
|
| |
\
|
\
0 0
0
1 1 1 c c
c c
j L j L C
j C L
| | | |
= = =
| |
\ \
Prof. T. L. Wu
Highpass Transformation
An inductive/capacitive element in the lowpass prototype will be inversely transformed to a
capacitive/inductive element in the highpass filter.
Example:
A practical highpass filter with a cutoff frequency at 2GHz and
50-ohms terminals, which is obtained from the transformation
of the 3 pole Butterworth lowpass prototype given above.
Prof. T. L. Wu
Bandpass Transformation
0
0 2 1
0
0 , , ,
c
c c
FBW
| |
=
|
\
2 1
0
FBW
=
0 1 2 =
-c c
0
0 0 0 0
0 0 0 0 0 0
0
1 1 1
,
1
c
p p
c c c
c
C FBW
C L
C C C FBW C
j j j
FBW FBW FBW
j
C
| | | |
= = = =
| |
| | | | \ \
+
| |
| | \ \
|
\
0
0 0 0 0
0 0 0 0 0
0 0
1 1
,
1
c c c
S S
c
c
FBW
j L j L j L C L L
FBW FBW FBW L FBW
j
L
| | | | | | | |
= = + = =
| | | |
| | \ \ \ \
|
\
Prof. T. L. Wu
Bandpass Transformation
An inductive/capacitive element g in the lowpass prototype will transform to a series/parallel LC
resonant circuit in the bandpass filter.
Prof. T. L. Wu
Bandstop Transformation
( )
1 2
c
0
0
0 , ,
c
c
FBW
w w
( )
0 0
0 0 0 0
0 0 0 0 0
0
1 1 1 1 1
,
c
s s
c c c c
FBW C
j C L
C FBW C FBW C FBW C FBW C
j j j
| |
= = + = =
|
| |
\
|
\
( )
0 0 0
0 0 0 0 0
0
0 0 0
1 1 1
,
1
c c
p p
c
c c
FBW FBW
j L j L C L L
FBW L
j
j FBW L FBW L
| | | |
= = = =
| |
\ \
+
c c
0 1 2 =
2 1
0
FBW
=
Prof. T. L. Wu
Bandstop Transformation
Opposite to the bandpass transformation, an inductive/capacitive element g in the lowpass
prototype will transform to a parallel/series LC resonant circuit in the bandstop filter.
Ex:
Prof. T. L. Wu
IMMITTANCE INVERTERS
Definition of Immittance, Impedance, and Admittance
Inverters
Filters with Immittance Inverters
Practical Realization of Immittance Inverters
Prof. T. L. Wu
Definition of Immittance
Immittance inverters are either impedance or admittance inverters.
An idealized impedance inverter is a two-port network that has a unique property at all
frequencies
if it is terminated in an impedance Z2 on one port, the impedance Z1 seen looking in at the
other port is
As can be seen, if Z2 is inductive/conductive, Z1 will become conductive/inductive, and
hence the inverter has a phase shift of 90 degrees or an odd multiple thereof.
K: characteristic impedance of the inverter
Prof. T. L. Wu
Impedance/admittance Inverter
the inverter has a phase shift of 90 degrees
Impedance/admittance inverters are also known as K-inverters / J-inverters.
The ABCD matrix of ideal impedance inverters may generally be expressed as
It is noted that the +/- 90 degree is decided by the phase of S
21
of the 2-port network
Prof. T. L. Wu
Filters with Immittance Inverters
A series inductance with an inverter on each side looks like a shunt capacitance from its exterior
terminals
A shunt capacitance with an inverter on each side looks likes a series inductance from its
external terminals
Inverters have the ability to shift impedance or admittance levels depending on the choice of K
or J parameters.
Making use of these properties enables us to convert a filter circuit to an equivalent form that
would be more convenient for implementation with microwave structures.
0 0
1 1 0
1 1
0 0 0 1 1
jK jK
j L
j C
jK jK
( (
( (
( (
=
( (
( (
( (
Proved by ABCD matrix
Prof. T. L. Wu
Lowpass Filters with Impedance Inverters
Prof. T. L. Wu
Lowpass Filters with Admittance Inverters
How to prove?
Take n=2 as an example
1 1
2
0 0 01
( / )
a
L g
Z g K
=
By expanding the input immittances of the original prototype networks and the
equivalent ones in continued fractions and by equating corresponding terms.
1
3 2
1
( )
1
Z s
g s
g sg
=
+
+
2
01
2
12
1 2
23
2
3
( )
a
a
K
Z s
K
sL
K
sL
Z
=
+
+
Compare their coefficients
1 0
01
1 0
a
L Z
K
g g
=
As an example
Prof. T. L. Wu
Bandpass Filters with Impedance Inverters
Since the source impedances are assumed the same in the
both filters as indicated, no impedance scaling is required.
Replace L
a1
transforming the inductors of the lowpass filter to the series
resonators of the bandpass filter, we obtain:
Prof. T. L. Wu
Bandpass Filters with admittance Inverters
Similarly
Prof. T. L. Wu
Generalized bandpass filters (including distributed
elements) using immittance inverters.
Reactance slope parameter for resonators having zero
reactance at center frequency
Susceptance slope parameter for resonators having
zero susceptance at center frequency
Prof. T. L. Wu
Practical Realization of Immittance Inverters
1 1 2
1 2
3 3
2
3 3
1
0
1
0 1
1
Z Z Z
Z Z
j L
Z Z
Z
j L
Z Z
(
+ + +
(
(
(
(
=
(
(
+
(
(
Z1
Z3
Z2
proof
+90
0
-90
0
+90
0
-90
0
Prof. T. L. Wu
Immittance inverters comprised of lumped and transmission line
elements
A circuit mixed with lumped and transmission line elements
Prof. T. L. Wu
Richards Transformation
lossless passive networks
p j = +
p j =
Distributed transmission line elements are of importance for designing practical microwave
filters.
A commonly used approach to the design of a practical distributed filter is to seek some approximate
equivalence between lumped and distributed elements.
Such equivalence can be established by applying Richardss transformation
Richards showed that distributed networks, comprised of commensurate length
(equal electrical length) transmission lines and lumped resistors, could be treated in
analysis or synthesis as lumped element LCR networks under the transformation
The new complex plane where t is defined is called the t-plane.
Following is referred to as Richards transformation
Prof. T. L. Wu
Richards Transformation
The periodic frequency response of the distributed filter network is demonstrated in Figure
3.23(b), which is obtained by applying the Richards transformation of (3.54) to the Chebyshev
lowpass prototype transfer function of (3.9), showing that the response repeats in frequency
intervals of 2w
0
.
A lowpass response in the p-plane may be mapped into either the lowpass or the bandstop one
in the t-plane, depending on the design objective. Similarly, it can be shown that a highpass
response in the p-plane may be transformed as either the highpass or the bandpass one in the
t-plane.
Prof. T. L. Wu
Richards Transformation
Lumped and distributed element correspondence
under Richards transformation
Prof. T. L. Wu
Richards Transformation
Another important distributed element, which has no lumped-element counterpart, is a two-
port network consisting of a commensurate-length line.
It is interesting to note that the unit element has a half-order transmission zero at t = 1.
Unit elements are usually employed to separate the circuit elements in distributed filters,
which are otherwise located at the same physical point.
Prof. T. L. Wu
Kuroda Identities
Such transformations not only provide designers with flexibility, but also are essential in many
cases to obtain networks that are physically realizable with physical dimensions.
Physically separate transmision line stubs
Transform series stubs into shunt stubs, or vice versa
Change impractical characteristic impedances into more realizable ones
Prof. T. L. Wu
Kuroda Identities
2
2
2
1 0 1
1
1 / 1
1
1
1
( 1/ ) 1
1
u
c u
u
c u c u
Z t
Y t t Z
t
Z t
Y Z t Y Z t
t
( (
( (
(
=
(
+ +
2
2 2
1
1 1
/ 1
0 1 1
1 ( )
1
1 / 1
u
c
u
u c
c
u
u
Z t
Z t
t Z
t
Z Z t
Z
t t Z t
Z
( (
(
(
(
(
+
(
=
(
+
(
Proof:
Prof. T. L. Wu
Kuroda identities
Prof. T. L. Wu
Coupled-Line Equivalent Circuits
I
2
0 0 1 1
0 0 2 2
2
1
2
2
cot csc
csc cot
/ 1
1
p
jZ jZ V I
jZ jZ V I
v I L L t
I t
t L L
( ( (
=
( ( (
(
(
( =
(
(
Coupled line Single line
Similar form
Proof: refer to Microwave Engineering
Prof. T. L. Wu
Coupled-Line Equivalent Circuits
Admittance matrix form
Prof. T. L. Wu
Coupled-Line Equivalent Circuits
It can be proved by ABCD parameters
Prof. T. L. Wu
Dissipation and unloaded quality factor
In reality, any practical microwave filter will have lossy elements with finite unloaded quality
factors in association with power dissipation in these elements.
Such parasitic dissipation may frequently lead to substantial differences between the response of
the filter actually realized and that of the ideal one designed with lossless elements.
Unloaded quality factor
For a lowpass or a highpass filter, is
usually the cutoff frequency; while for a
bandpass or bandstop filter, is the center
frequency.
is the resonant freq. for the lossy
resonator
Prof. T. L. Wu
Dissipation Effect on Lowpass and Highpass Filters
Assuming that the unloaded quality factors of all reactive elements in a filter are known,
determined theoretically or experimentally, we can find R and G for the lossy reactive elements
from previous equations. The dissipation effects on the filter insertion loss response can easily
estimated by analysis of the whole filter equivalent circuit, including the dissipative elements R and
G.
Another approach based on simple formula by Cohn (1959)
Prof. T. L. Wu
Dissipation Effect on Lowpass and Highpass Filters
As an example, let us consider the lowpass filter designed previously in Figure 3.13, which has a Butterworth
response with a cutoff frequency at fc = 2 GHz. To take into account the finite unloaded quality factors of the
reactive elements, the filter circuit becomes that of Figure below.
1. A shift of insertion loss by a constant amount determined by the additional loss at zero
frequency.
2. A gradual rounding off of the insertion loss curve at the passband edge, resulting in
diminished width of the passband and hence in reduced selectivity.
Two effects are obvious:
Prof. T. L. Wu
Dissipation Effect on Bandpass and Bandstop Filters
It should be mentioned that not only does the passband insertion loss increase and the selectivity
become worse as the Qu is decreased, but it also can be shown that for a given Qu, the same
tendencies occur as the fractional bandwidth of the filter is reduced.
Prof. T. L. Wu
HW #1
Prove equation (3.24) for Butterworth Lowpass Prototype Filter
Prove the equations shown in Fig. 3.18(a) and Fig. 3.18(b).
Prove the equations shown in Fig. 3.19(a) and Fig. 3.19(b).
Please prove the reactance slope parameters of a lumped LC series resonator is
0
L, and the susceptance
slope parameters of a lumped LC parallel resonator is
0
C.
Prove the equations shown in Fig. 3.20(a) and Fig. 3.20(b).
Please prove Fig. 3.21(a) & (d) have a phase shift of +90 degree, and Fig. 3.21(b) & (c) have a phase shift
of -90 degree.
Please prove the identities in Fig. 3.27.
Das könnte Ihnen auch gefallen
- Microwave FiltersDokument20 SeitenMicrowave FiltersDiptiman BiswasNoch keine Bewertungen
- Solution Manual for 100 Genesys Design Examples: Second EditionVon EverandSolution Manual for 100 Genesys Design Examples: Second EditionNoch keine Bewertungen
- Microwave Filters-1965Dokument20 SeitenMicrowave Filters-1965alokcena007Noch keine Bewertungen
- Advanced Synthesis Techniques For Microwave Filters - Richard J CameronDokument19 SeitenAdvanced Synthesis Techniques For Microwave Filters - Richard J CameronMinh VuNoch keine Bewertungen
- Microwave Filter DesignDokument50 SeitenMicrowave Filter Designsimsook91100% (1)
- Modeling of Digital Communication Systems Using SIMULINKVon EverandModeling of Digital Communication Systems Using SIMULINKNoch keine Bewertungen
- Design and Simulation of A Multilayer Dual Behavior Resonator Microwave FilterDokument5 SeitenDesign and Simulation of A Multilayer Dual Behavior Resonator Microwave FilterViteriNoch keine Bewertungen
- Partial-Update Adaptive Signal Processing: Design Analysis and ImplementationVon EverandPartial-Update Adaptive Signal Processing: Design Analysis and ImplementationNoch keine Bewertungen
- Microwave Filter DesignDokument106 SeitenMicrowave Filter Designgirinaag10Noch keine Bewertungen
- Introduction to Optical Waveguide Analysis: Solving Maxwell's Equation and the Schrödinger EquationVon EverandIntroduction to Optical Waveguide Analysis: Solving Maxwell's Equation and the Schrödinger EquationNoch keine Bewertungen
- 08 HirtenfelderDokument42 Seiten08 HirtenfelderMazigh HoudNoch keine Bewertungen
- Microstrip Patch AntennaDokument23 SeitenMicrostrip Patch AntennaKaluwaNoch keine Bewertungen
- (0.5) A History of Microwave Filter Research, Design, and DevelopmentDokument15 Seiten(0.5) A History of Microwave Filter Research, Design, and Developmentsanjeevsoni64Noch keine Bewertungen
- Reflector Antenna System DesignDokument35 SeitenReflector Antenna System DesignAyyem Pillai VNoch keine Bewertungen
- CHP4-MICROWAVE FILTERS - WithexamplesDokument71 SeitenCHP4-MICROWAVE FILTERS - WithexamplesAnonymous VoetONtGnNoch keine Bewertungen
- FilterDesign and HFSS HODokument22 SeitenFilterDesign and HFSS HOOlalere KolawoleNoch keine Bewertungen
- Narrowband Microstrip Filter DesignDokument48 SeitenNarrowband Microstrip Filter DesigndwisselNoch keine Bewertungen
- CST Studio Suite - FEST3D User ManualDokument661 SeitenCST Studio Suite - FEST3D User ManualZain100% (1)
- 6-2-4 CST EucDokument30 Seiten6-2-4 CST EucDo SonNoch keine Bewertungen
- Antenna Array Analysis and SynthesisDokument37 SeitenAntenna Array Analysis and SynthesisMani Raaz0% (1)
- Coupled Line Bandpass FilterDokument70 SeitenCoupled Line Bandpass Filterash9977100% (2)
- Microstrip Patch AntennaDokument20 SeitenMicrostrip Patch AntennaAnuragNoch keine Bewertungen
- Modeling and Design of Microwave-Millimeterwave Filters and MultiplexersDokument314 SeitenModeling and Design of Microwave-Millimeterwave Filters and MultiplexersFilete de FaleteNoch keine Bewertungen
- Experiment No.1 Rectangular Waveguide Design Using CST Microwave Studio SuiteDokument3 SeitenExperiment No.1 Rectangular Waveguide Design Using CST Microwave Studio Suiteali saleh100% (1)
- Port Tutorial Lump V WaveDokument11 SeitenPort Tutorial Lump V WavePablo MontesNoch keine Bewertungen
- Guidelines For Meshing in Ansoft HFSSDokument19 SeitenGuidelines For Meshing in Ansoft HFSSAshutosh BahetiNoch keine Bewertungen
- Microstrip Antenna PDFDokument17 SeitenMicrostrip Antenna PDFDhivya Dhanalakshmi ECENoch keine Bewertungen
- Antenna Gs PDFDokument182 SeitenAntenna Gs PDFgogu vasileNoch keine Bewertungen
- 1 BasicDokument39 Seiten1 BasicanililhanNoch keine Bewertungen
- Content Beyond Syllabus-Microwave FiltersDokument36 SeitenContent Beyond Syllabus-Microwave FiltersAnonymous 8E7uRzNoch keine Bewertungen
- Radar Cross SectionDokument9 SeitenRadar Cross SectionConstantin DorinelNoch keine Bewertungen
- Low-Loss, Broadly-Tunable Cavity Filter Operating at UHF FrequenciesDokument4 SeitenLow-Loss, Broadly-Tunable Cavity Filter Operating at UHF FrequenciesDo SonNoch keine Bewertungen
- 1-1 Patch Antenna Design Using Ansoft DesignerDokument53 Seiten1-1 Patch Antenna Design Using Ansoft DesignerAlainN2200Noch keine Bewertungen
- 4 1 2 Uwb Antenne Simulation With CST Microwave StudioDokument24 Seiten4 1 2 Uwb Antenne Simulation With CST Microwave StudioUmair SaleemNoch keine Bewertungen
- 04 MW Microwave Dividers CouplersDokument88 Seiten04 MW Microwave Dividers CouplersJulie ThorNoch keine Bewertungen
- Infinitesimal Dipole Antennas2Dokument35 SeitenInfinitesimal Dipole Antennas2Anonymous XV3SIjz8bNoch keine Bewertungen
- Boundary and Excitation Training: February 2003Dokument30 SeitenBoundary and Excitation Training: February 2003Sandrine GallardNoch keine Bewertungen
- Sub Harmonic Mixer Design With Ansoft DesignerDokument35 SeitenSub Harmonic Mixer Design With Ansoft DesignerNaga NikhilNoch keine Bewertungen
- Hfss ProjectsDokument7 SeitenHfss Projectssandeepsrikumar100% (1)
- Antenna Assignment1Dokument14 SeitenAntenna Assignment1karthikrao191919Noch keine Bewertungen
- 3 Design of RF and Microwave FiltersDokument44 Seiten3 Design of RF and Microwave Filterswearole100% (2)
- FSS CST TutorialDokument10 SeitenFSS CST TutorialIftikhar Ahmed100% (1)
- An Introduction To HFSS OptimetricsDokument52 SeitenAn Introduction To HFSS OptimetricsdhruvaaaaaNoch keine Bewertungen
- Directional CouplersDokument10 SeitenDirectional Couplersnamhoa02Noch keine Bewertungen
- Microwave Filter DesignDokument7 SeitenMicrowave Filter DesignduwuNoch keine Bewertungen
- 2.microwave Engineering PDFDokument82 Seiten2.microwave Engineering PDFsankeerthanreddyNoch keine Bewertungen
- Antenna 2Dokument15 SeitenAntenna 2Jaskirat Singh ChhabraNoch keine Bewertungen
- Effect of Antenna Size On Gain BandwidthDokument14 SeitenEffect of Antenna Size On Gain BandwidthNgoc Lan NguyenNoch keine Bewertungen
- ParallelCoupledBandpassFilter PDFDokument38 SeitenParallelCoupledBandpassFilter PDFKis BelaNoch keine Bewertungen
- Hfss Tutorial CPWDokument21 SeitenHfss Tutorial CPWFAROOQ Tahir67% (3)
- HFSS Antennas - Arrays PDFDokument37 SeitenHFSS Antennas - Arrays PDFYohandriNoch keine Bewertungen
- In CST To Choose A Point That Lies in The Center Between Two PointsDokument10 SeitenIn CST To Choose A Point That Lies in The Center Between Two PointsAlfredo DezoNoch keine Bewertungen
- Aperture Coupled Fed Micro-Strip Patch AntennaDokument5 SeitenAperture Coupled Fed Micro-Strip Patch AntennaemremiranNoch keine Bewertungen
- Antenna and Wave Propagation (EEE) - EEC708Dokument5 SeitenAntenna and Wave Propagation (EEE) - EEC708Mayur BundelNoch keine Bewertungen
- EDICONChina2019 - (87) - Vye, David - Designing A Narrowband 28-GHz Bandpass Filter For 5G Applications PDFDokument41 SeitenEDICONChina2019 - (87) - Vye, David - Designing A Narrowband 28-GHz Bandpass Filter For 5G Applications PDFkhyatichavdaNoch keine Bewertungen
- Antenna 5Dokument30 SeitenAntenna 5Frederico MailaNoch keine Bewertungen
- 2.45GHz Patch AntennaDokument7 Seiten2.45GHz Patch AntennawearoleNoch keine Bewertungen
- Course OutlineDokument4 SeitenCourse OutlineSalome ChivimaNoch keine Bewertungen
- Module 1-Introduction and Image Parameter MethodDokument83 SeitenModule 1-Introduction and Image Parameter MethodTanvi DeoreNoch keine Bewertungen
- Updated RFD Lab Manual PDFDokument46 SeitenUpdated RFD Lab Manual PDFAminaMouhoucheNoch keine Bewertungen
- RF Filter Part 1Dokument47 SeitenRF Filter Part 1Tuhin DuttaNoch keine Bewertungen
- Design of Low Pass Filter Using Micro Strip LinesDokument14 SeitenDesign of Low Pass Filter Using Micro Strip LinesSakshiKoulNoch keine Bewertungen
- Lecture 31: Filter Implementation: 1 ELEC4630, Shu Yang, HKUSTDokument18 SeitenLecture 31: Filter Implementation: 1 ELEC4630, Shu Yang, HKUSTAlejandro GudiñoNoch keine Bewertungen
- Richard's TransformationDokument7 SeitenRichard's Transformationservice infoNoch keine Bewertungen
- Microstrip Notch FilterDokument22 SeitenMicrostrip Notch FilterGöksenin BozdağNoch keine Bewertungen
- Design, Simulation and Implementation of Very Compact Dual-Band Microstrip Bandpass Filter For 4G and 5G ApplicationsDokument4 SeitenDesign, Simulation and Implementation of Very Compact Dual-Band Microstrip Bandpass Filter For 4G and 5G ApplicationsTran TommyNoch keine Bewertungen
- 6.2 Filters BPFDokument26 Seiten6.2 Filters BPFThanh HàNoch keine Bewertungen
- Band Pass Filter Design Example PDFDokument18 SeitenBand Pass Filter Design Example PDFShrutiAwasthiNoch keine Bewertungen
- E 412 F 04 Lec 13Dokument19 SeitenE 412 F 04 Lec 13Vedran IbrahimovicNoch keine Bewertungen
- Microwave FiltersDokument34 SeitenMicrowave FiltersLinh TajNoch keine Bewertungen
- Band-Pass Filter Design ExampleDokument18 SeitenBand-Pass Filter Design ExampleFa Mido ChemseddineNoch keine Bewertungen
- Module 1-Insertion Loss MethodDokument46 SeitenModule 1-Insertion Loss MethodTanvi DeoreNoch keine Bewertungen
- Microwave Filters: Prof. D. Kannadassan, School of Electronics EngineeringDokument23 SeitenMicrowave Filters: Prof. D. Kannadassan, School of Electronics EngineeringAkshay GuptaNoch keine Bewertungen
- Chp4 Microwave FiltersDokument77 SeitenChp4 Microwave FiltersRavindra KumarNoch keine Bewertungen
- Introduction To RF Filter Design: RF Electronics Spring, 2018 Robert R. Krchnavek Rowan UniversityDokument47 SeitenIntroduction To RF Filter Design: RF Electronics Spring, 2018 Robert R. Krchnavek Rowan UniversityBisuNoch keine Bewertungen