Design and Analysis of Nuclear Steam Generator

Components Using CFX-5

M. H. Hu
Westinghouse Electric Company
Madison, PA
Abstract
A nuclear power plant U-Tube steam generator is a boiling heat exchanger with shell and tubes. Feed
water enters the generator as subcooled water and goes through a series of components to distribute into
tube bundle. In the tube bundle, the subcooled water boils, leaves the bundle as a mixture of steam and
water, and rises through moisture separation devices. Saturated water returns to a water pool where the
feed water enters and mixes with the saturated water. Steam continues rising up and leaves the steam
generator. Each component has its unique fluid conditions ranging from single phase to two-phase flow
plus corrosion particles and solute. Modules of CFD analysis for various components are being developed
using the CFX-5 program. This paper presents four modules: (1) the lower tube bundle, (2) the sludge
collector in the water pool, (3) the steam flow through the last stage of moisture separation, and (4) the feed
water distribution ring. This paper presents results of the CFX-5 CFD analysis for these modules. The
paper demonstrates the CFX-5 role and its usefulness in the design and analysis of the nuclear steam
generator. The continued module development will cover more components, in particular, in the tube
bundle where boiling takes place. For example, it is planned to evaluate steam and water flow through the
restricted passage of the tube support plate so that particulate deposition and solute precipitation in the
restricted passage can be examined and prevented.
Introduction
As a component of pressurized water reactor (PWR) power plant, a steam generator is a boiling heat
exchanger that uses the reactor coolant as heat source to bring water into steam. Figure 1 illustrates a
nuclear steam generator that consists of thousands of U-shaped tubes through which the reactor coolant
passes and transfer heat to water outside the tubes. Within the tube bundle water boils and two-phase flow
results. Water is separated from the two-phase flow by the primary and secondary moisture separator.
Steam then leaves the steam nozzle and continues to the steam turbine. Feed water constantly supplies the
water mass to compensate the mass that evaporates and leaves the generator. Feed water brings with it the
corrosion products of either particulates or dissolved chemicals from upstream piping and components.
Therefore, water, vapor and corrosion products can form multiple phases in the tube bundle flow. In
summary, the steam generator thermal and hydraulic flow ranges from single phase to two-phase to
multiple phases. Depending on size of fluid domain in the tube bundle, fluid flow can be treated as either
the fluid flow with discrete solids or porous media flow.
It may be feasible to simulate the whole steam generator with just one model of computational fluid
dynamics (CFD). However, it is practical and flexible to approach the whole steam generator as a variety
of modules in setting up CFD analysis. After many years of searching and usage of different CFD codes,
we finally settled on CFX CFD codes. In the beginning, we contracted the CFD analysis to outside firms.
For example, we had had ANSYS CFX to simulate flow in the upper, water pool, and the flow in the feed
water distribution ring. We finally convinced the management to use the CFD analysis and steadily build
up the in-house capability in applying the CFX-5 code. This paper is to present our successful modules of
the CFX-5 CFD analysis for the nuclear steam generator.
Modules
We are continuing building CFD modules for a variety of needs in design and trouble shooting of the steam
generator. The paper will present four modules to date.


























Figure 1. Schematic of a Steam Generator
Module 1 Flow at Tube Sheet
Figure 2 depicts Module 1 to simulate flow at tube sheet of the steam generator. It consists of flow in the
downcomer and tube bundle. At the bottom end of the downcomer, a groove can relieve stress at the joint
between the shell and the tube sheet. The design with the groove is new, and the designer wants to know
that such a groove will not compromise the fluid flow functions inside the tube bundle. For example, use
of the groove should neither trigger the flow induced tube vibration, nor increase amount of settlement of
sludge particles on top of the tube sheet.

Downcomer
Tube Sheet
Water Level &
Water Pool
Outer Shell
Channel Head
Hot Leg:
Coolant
Inlet
Feed Water
Distribution Ring
Primary Separator
Tube Support Plate
Secondary Separator
Feed Water Flow
Wrapper
U-Tube
Cold Leg:
Coolant
Outlet
Sludge collector
Steam Nozzle
Downcomer
Tube Sheet
Water Level &
Water Pool
Outer Shell
Channel Head
Hot Leg:
Coolant
Inlet
Feed Water
Distribution Ring
Downcomer
Tube Sheet
Water Level &
Water Pool
Outer Shell
Channel Head
Hot Leg:
Coolant
Inlet
Feed Water
Distribution Ring
Primary Separator
Tube Support Plate
Secondary Separator
Feed Water Flow
Wrapper
U-Tube
Cold Leg:
Coolant
Outlet
Sludge collector
Primary Separator
Tube Support Plate
Secondary Separator
Feed Water Flow
Wrapper
U-Tube
Cold Leg:
Coolant
Outlet
Sludge collector
Steam Nozzle Steam Nozzle














Figure 2. Zone of CFD Simulation at the Tube Sheet with Groove (Dimension in mm)

A scoping assessment concludes that effect of the groove would be negligible to the fluid conditions inside
the wrapper where the tube bundle resides. The tube bundle consists of about 5800 tubes with 19 mm in
diameter, and 27 mm in tube pitch in square layout. As expected, flow perturbation due to the groove feeds
into the tube bundle. However, its effect should be quickly dissipated within 2 or 3 tube rows from the
periphery of the tube bundle because the flow resistance due to the tube bundle is orders of magnitude
higher than the flow resistance due to the groove.
To confirm this conclusion, we set up a CFD simulation over a fluid domain that covers from the top of the
tube sheet to the second tube support plate. An 180
o
model was used with a tube lane that is relatively open
without tubes as shown in Figure 2. Along the tube lane fluid flow is at relatively higher velocity than that
through the regions where tubes exist.
During normal operation, it is expected to see boiling in certain zone of the tube bundle because of heat
transfer from the reactor coolant to the secondary side water. However, we consider it adequate to simulate
just the hydraulic effect without heat transfer. Two simulations were done with and without the groove,
respectively. The boundary conditions are (1) uniform velocity at 4.36 m/s at the inlet of the downcomer
and (2) uniform pressure at the top of the second tube support plate. The second boundary condition is
assumed according to a simulation of the whole tube bundle by ATHOS code (Reference 1) that showed a
fairly uniform pressure at the second tube support plate. Therefore, use of uniform pressure boundary
condition is sound for comparative evaluation between design with and without a groove. The built-in k-
turbulence model was used. The tube bundle was treated as an anisotropic porous medium with momentum
sinks. The momentum sinks take the following expressions.
U U C S x x x R x M , 2 ,
=
U U C S y y y R y M , 2 ,
=
U U C S z z z R z M , 2 ,
=
For the tube bundle in cross flow,

60
30
3686
3506
L
o
w
e
r
S
h
e
l
l
Groove
W
r
a
p
p
e
r
D
o
w
n
c
o
m
e
r
1st Tube Support Plate
2nd Tube Support Plate
Hot Leg
Cold Leg
Outlet Boundary
Inlet Inlet
56.20
50
200 Wrapper Opening T
u
b
e

L
a
n
e
2
1
0
4
60
30
3686
3506
L
o
w
e
r
S
h
e
l
l
Groove
W
r
a
p
p
e
r
D
o
w
n
c
o
m
e
r
1st Tube Support Plate
2nd Tube Support Plate
Hot Leg
Cold Leg
Outlet Boundary
Inlet Inlet
56.20
50
200 Wrapper Opening T
u
b
e

L
a
n
e
2
1
0
4
|
.
|

\
|

|
|
.
|

\
|
|
|
.
|

\
|
=
D S
S
S g
f
C
o L
L
L
c
x R
2
, 2
1
2


The coefficient C
R2,y
has the same expression as the C
R2,x
. The friction factor (Ref. 2) is as below.
(
(
(
(
(
(
(

+ =
|
.
|

\
|

|
.
|

\
|

D
D S
S D
D
S
D U
D S
S
f
o
o L
L
o
L
b
o
o T
T
o
/ 13 . 1 43 . 0
15 . 0
08 . 0
044 . 0

In the above expression, the cross flow velocity U is either U
x
or U
y
.
For the tube bundle in parallel flow,
|
|
.
|

\
|

|
|
.
|

\
|
|
|
.
|

\
|
=
D S S
S S
D
g
f
C
o T L
T L
e
c
z R
2
2
, 2
4
1
2

Where the friction factor (Ref. 3) is as below
|
|
.
|

\
|

D U
D S S
S S
f
e z
o T L
T L
2
2 . 0
4
046 . 0
For the tube support plate,
|
|
.
|

\
|

|
|
.
|

\
|
|
|
.
|

\
|
=
D S S
S S
Z
K
g
C
o L T
L T
TSP
c
z R
2
2
, 2
4
2

For present simulation, we have the following:
D
e
29.67 mm (Tube bundle hydraulic diameter)
D
o
19.05 mm (Tube OD)
g
c
1 g-cm/dyne-sec
2

S
L
27 mm (Tube pitch in longitudinal direction)
S
T
27 mm (Tube pitch in transverse direction)
K 2.53 (Loss coefficient of tube support plate)
Z
TSP
29 mm (Thickness of tube support plate)
778.6 kg/m
3
(Water density)

o
1.016E-04 Pa-sec (Dynamic viscosity of water)

Using the above values, we have calculated the friction factors over a range of velocity (0.34 to 5 m/s). Of
course, the loss coefficient depends on velocity. However, their average value is a good approximation for
simplicity. The average is 0.0484 and 0.0032 for the cross and parallel flow, respectively. Finally, the
coefficient of the momentum sinks is calculated and results are shown below.

Coefficient Value, kg/m
4

Remark
C
R2,x
32185
Normal to Tube Bundle
C
R2,y
32185
Normal to Tube Bundle
C
R2,z
450
Parallel to Tube Bundle
C
R2,z
142698
Normal to Tube Support Plate

Results of convergent solutions were obtained and analyzed. Figures 3a and 3b depict velocity contours at
a plane 2.5 centimeters above the tube sheet that is perpendicular to the tube bundle. These velocity
contours represent magnitude of the cross flow velocity in meters per second. When the cross flow
velocity is smaller than a threshold of 0.3 m/s, the sludge particle will settle on the top of the tube sheet. A
close comparison between Figure 3a with a groove and Figure 3b without a groove didnt show discernable
difference. Therefore, use of the groove will not increase amount of sludge settlement at the tube sheet.
Around 90
o
, the velocity contours penetrate much deeper because it is along the tube lane where no tubes
exist and thus flow resistance is much less, compared to the tube bundle zone. Such a flow behavior as
shown in Figure 3b is also obtained by a special purpose code called ATHOS (Ref. 1) that uses different
approach in simulating the porosity of the tube bundle.
Figure 4 presents velocity components along two selective tubes for both simulations with and without the
groove. The difference in values of the velocity is negligible so that no difference in flow induced tube
vibration is expected. Results of CFD calculation confirm that effect of the groove is negligible to flow
conditions inside the tube bundle.

Figure 3a. Velocity Contours on the Plane 2.5 cm above Top of Tube Sheet with a Groove


Figure 3b. Velocity Contours on the Plane 2.5 cm above Top of Tube Sheet without a
Groove


0.00
0.20
0.40
0.60
0.80
1.00
1.20
1.40
1.60
0.00 0.50 1.00 1.50 2.00 2.50
Elevation, m
V
e
l
o
c
i
t
y
,

m
/
s
Velocity, Non-G(180), T#1
Velocity,W/G(180), T#1
Velocity, Non-G(180), T#2
Velocity, W/G(180), T#2

Figure 4. Value of Velocity along Two Selective Tubes (Non-G (180): 180
o
Model without a
Groove, W/G (180): 180
o
Model with a Groove, T#1: Tube #1, and T#2: Tube #2)
Module 2 Steam Flow through Secondary Separator
Figure 5 depicts a CFX-5 CFD model for steam flow through the space from the exit of the primary
separator, through the secondary separator to the steam nozzle. Purpose of this CFD simulation is to
estimate the range of transport time of sodium tracer through this space. The assumption is that the sodium
tracer would travel at the same velocity as steam does. A 45
o
sector was modeled with steam flow entering
the fluid domain at the exits of the primary separator and leaving the domain at the steam nozzle (see
Figure 5). The secondary separator consists of tortuous paths for capturing moisture. In addition, those
black bodies are solid cutouts where no fluid flow exists. Similar to the tube bundle in Module 1, the
secondary separator is treated as porous medium with the use of fluid sub-domain for introducing
momentum sinks. The steam inlet velocity from each orifice opening varies from 11.2 m/s to 13.3 m/s and
the outlet is at relative pressure of 0 Pa. The system pressure is 5.45 MPa, and reference temperature is
269.3
o
C for this isothermal problem. Flow area of the outlet is so small compared to the dimension of the
fluid domain, and thus, use of 0 Pa at the outlet is practical and valid.
The built-in k- turbulence model was selected and convergent solution was obtained. Rigorous approach
of solving the transport time was instructed by ANSYS CFX Technical Support Center (Ref. 4), but was
not used in this analysis. Transport time of the sodium tracer is considered to be the time taken by steam
along the streamlines. Figure 6 depicts the transport time started at one of the orifice openings. As shown,
the transport time ranges from about 1.2 to 2.2 seconds. Use of the streamline yields quick, approximate
estimates of the transport time.
In fact, results of this CFD calculation is also of great use in understanding other mechanisms of moisture
separation. Granted, moisture droplets would travel paths other than those at the steam. However, as an
approximation, we can assume that moisture droplets travel with the steam at the same velocity. We see
some streamlines end up at the wall and never reach the steam nozzle. Therefore, the wall of the shell or
the solid cutout does serve the role of moisture separation. As depicted in Figure 7 for Orifice Inlet No. 2,
one of four streamlines reaches the steam nozzle, and the other three terminate on the wall and thus the
moisture droplets are separated by wall. Therefore, it appears that certain locations of the steam flow inlet
to the secondary separator may enhance the moisture separation, such as the Orifice Inlet No. 2 that is
directly below the bottom cover of the separator, and thus encourages the moisture droplets to divert to the
wall.










Figure 5. Geometry of Secondary Separator and CFX Model with Boundary Openings
Mid Deck Plate
Opening to Steam Nozzle
x
Sector I
Sector II Sector III
Sector IV
y
8
1
2
3
4
5 6
7
8 Orifices on Mid Deck Plate
428 cm
4
2
0

c
m
Lower Tier of
Secondary
Separator
Upper Tier of
Secondary
Separator
Solid Cutout
Mid Deck Plate
Opening to Steam Nozzle
x
Sector I
Sector II Sector III
Sector IV
y
8
1
2
3
4
5 6
7
8 Orifices on Mid Deck Plate
428 cm
4
2
0

c
m
Lower Tier of
Secondary
Separator
Upper Tier of
Secondary
Separator
Solid Cutout
Mid Deck Plate
Opening to Steam Nozzle
x
Sector I
Sector II Sector III
Sector IV
y
8
1
2
3
4
5 6
7
8 Orifices on Mid Deck Plate
428 cm
4
2
0

c
m
Lower Tier of
Secondary
Separator
Upper Tier of
Secondary
Separator
Solid Cutout

Figure 6. Steam Transit Time from Outer Orifice-Inlet (No. 8) to Steam Nozzle Outlet


Figure 7. Steam Transit Time from Inner Orifice-Inlet (No. 2) to Steam Nozzle Outlet

Module 3 Flow inside and outside a Sludge Collector
Figure 8 shows a CFX-5 CFD model to simulate flow inside and outside a sludge collector. A sludge
collector is to trap the sludge particle. Sludge deposit on the tube wall could cause tube corrosion and
reduce heat transfer. A sludge collector that sits in the water pool that is outside the tube bundle is a
desired device. The sludge collector had been verified and confirmed in field operation to capture sludge.
Purpose of a CFX-5 CFD analysis is to quantify and optimize the collector design.
Flow outside the collector is chaotic. It is critical to properly locate the inlet and outlet holes. Figure 8
shows that the inlet holes draw the water into the collector and the outlet holes allow the water to leave.
During the passage of the water through the collector, sludge particles will settle due to its being heavier
than water. It is desirable to draw adequate water to maximize the amount of sludge mass and yet to avoid
re-entraining effect. If the flow rate through the collector is too high, the particle may not have time to
settle, and worse yet the settled particles can be picked up again (i.e. re-entrained into the water flow).
The overall fluid domain of the CFD model consists of boundary conditions, solid cutouts with velocity
boundaries, and thin plates to simulate the outer covers and inner floors for sludge to settle. This collector
has three floors with the bottom one having largest floor area. There are four fluid flow inlets in the model.
Inlets 1 to 3 are for saturated water that is separated from steam and returned to the water pool at different
locations. Such recirculated, saturated water is at 276.9
o
C and a flow rate of 283 kg/s with 10% via Inlets 1
and 3, each, and the remaining 80% via Inlet 2. Inlet 4 provides feed water at 227.3
o
C and a flow rate of
103 kg/s. The outlet is at a relative pressure of 0 Pa and the system pressure is 6.13 MPa. Flow area at the
outlet boundary is small compared to the dimension of the overall fluid domain, and thus use of zero
pressure at the outlet is a practical approximation. The built-in k- turbulence model was selected and
convergent solution was obtained. Results of the convergent solution were captured through the user
defined surfaces for the eight inlet holes and outlet holes, respectively. Table 1 summarized the flow rate
through these eight inlet and outlet holes, respectively. Flow rate through the inlet holes is summed to 0.69
kg/s, about equal to that through the outlet hole. The total flow through the model is 103 kg/s and thus the
collector flow of 0.69 kg/s is relatively small. Yet, the CFX-5 model is able to solve such a big contrast in
flow between the overall model and the collector. Of course, it took much effort in solution control to
finally obtain the convergent solution. It is considered that CFX-5 is a good CFD tool to produce result for
a complicated problem like this.

Table 1. Flow Rate and Velocity through Inlet and Outlet Holes

Inlet Hole Flow Rate, kg/s Velocity, m/s Outlet Hole Flow Rate, kg/s Velocity, m/s
1 -0.046 -0.19 1 0.102 0.43
2 -0.022 -0.09 2 0.092 0.39
3 -0.060 -0.25 3 0.081 0.34
4 -0.115 -0.48 4 0.073 0.31
5 -0.046 -0.20 5 0.069 0.29
6 -0.126 -0.53 6 0.075 0.32
7 -0.151 -0.64 7 0.095 0.40
8 -0.118 -0.50 8 0.104 0.44
Average -0.086 -0.36 Average 0.086 0.36

Figure 9 plots temperature on wall of various components. The red color is at 276.9
o
C and the blue at
227.3
o
C and those in between are due to mixing of saturated water and feed water. The cover of the
collector where the inlet holes are located is essentially in red that indicates that only the saturated water
enters the collector. The saturated water has a higher concentration of sludge particles than the feed water,
and thus is desirable. Flow velocity through the sludge collector ranges from 0.05 to 0.10 m/s that are
below the re-entrainment velocity. Sludge particles entering with the water would settle on the three floors
in the collector. There is room for optimizing the amount of the sludge settlement in the collector. This
can be achieved by increasing the diameter of the inlet holes and increasing the floor space by extending
the radial edge toward the shell of the steam generator.






Figure 8. Schematic and CFX CFD Model for Fluid Domain With Sludge Collector in the
Lower Left Corner


Figure 9. Temperatures on Wall of Various Components
Flow Outlet
Flow Intlet 1
F
l
o
w

I
n
t
l
e
t
3
Flow Intlet 4
Flow
Intlet 2
Sludge
Collector
Solid Cutouts
Cover
Inlet Holes Outlet Holes
241 cm
2
1
8

c
m
O
u
t
l
e
t

h
o
l
e
s
Inlet holes
Holes on Cover
(2 cm Diameter)
1
,
2
3
,
4
,
5
6
,
7
,
8
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
Flow Outlet
Flow Intlet 1
F
l
o
w

I
n
t
l
e
t
3
Flow Intlet 4
Flow
Intlet 2
Sludge
Collector
Solid Cutouts
Cover
Inlet Holes Outlet Holes
241 cm
2
1
8

c
m
Flow Outlet
Flow Intlet 1
F
l
o
w

I
n
t
l
e
t
3
Flow Intlet 4
Flow
Intlet 2
Sludge
Collector
Solid Cutouts
Cover
Inlet Holes Outlet Holes
241 cm
2
1
8

c
m
O
u
t
l
e
t

h
o
l
e
s
Inlet holes
Holes on Cover
(2 cm Diameter)
1
,
2
3
,
4
,
5
6
,
7
,
8
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
O
u
t
l
e
t

h
o
l
e
s
Inlet holes
Holes on Cover
(2 cm Diameter)
1
,
2
3
,
4
,
5
6
,
7
,
8
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
Module 4 Distribution of Feed Water Flow
Figure 10 illustrates a schematic of a feed water distribution system into a steam generator. It is desirable
to have a uniform distribution of feed water via the top-mounted spray tubes into the water pool in the
steam generator. In addition, local velocity distribution for each spray tube would be of great use in
assessing the erosion-corrosion potential. The feed water distribution system consists of an inlet pipe, a
Tee, a reducer and a ring with constant diameter. There are two tubes on top of the Tee. There are 31
tubes on the ring with a tube pitch of 4.7
o
.
The boundary conditions are (1) uniform inlet velocity at the pipe inlet, and (2) constant pressure at exit
windows of spray tubes. The built-in k- turbulence model is used in the simulation. Result of convergent
solution was captured for each discharging window of each spray tube. Table 2 tabulates the average
velocity and mass flow rate through each spray tube. Discharge flow is not uniform among all 33 spray
tubes. The first two spray tubes have the highest discharge rate this is because the feed water flow
impinges on the back side of the Tee and turns, and thus flow slows down and kinetic energy transform into
potential energy. Therefore, the pressure differential from the inlet to the outlet of the spray tube is highest
for the 1
st
and 2
nd
spray tube (see Figure 11). When feed water flow leaves the reducer and gets into the
ring, the flow speeds up at the expense of the pressure. Therefore, the pressure differential for the spray
tubes in this portion of the ring is low, and the discharge rate or velocity is relatively small. When the feed
water flow approaches the end of the ring, it slows down and thus pressure increases. Therefore, the
discharge rate and velocity is relatively high within the rear portion of the feed ring.

Table 2. Flow Rate and Velocity through Each Spray Tube
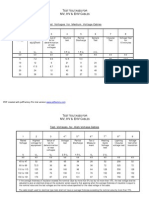
Spray Tube No. Flow Rate,
kg/s
% of Total
Flow
Spray Tube
No.
Flow Rate,
kg/s
% of Total
Flow
1 18.67 6.18 18 5.02 1.66
2 16.96 5.61 19 4.96 1.64
3 3.94 1.30 20 11.91 3.94
4 3.41 1.13 21 11.08 3.67
5 2.89 0.96 22 13.20 4.37
6 3.07 1.02 23 13.81 4.57
7 2.90 0.96 24 13.94 4.62
8 2.90 0.96 25 14.83 4.91
9 3.61 1.20 26 14.92 4.94
10 3.39 1.12 27 15.65 5.18
11 3.66 1.21 28 15.93 5.27
12 4.46 1.48 29 15.95 5.28
13 3.67 1.21 30 16.30 5.40
14 3.33 1.10 31 16.05 5.31
15 4.44 1.47 32 13.01 4.31
16 4.15 1.37 33 12.56 4.16
17 7.48 2.48

Figure 12 depicts velocity vector on the symmetry plane of the inlet pipe and outlets of certain spray tubes,
and velocity contours on the symmetry plane in the Tee and reducer. Each spray tube has different
discharge flow pattern, and it shows circumferential and axial variation within each spray tube. The
difference in flow conditions among spray tubes may be responsible for whether erosion-corrosion may
occur in specific tube. Figure 12 indicates that Spray Tube Nos. 1 and 2 can have velocity as high as 11
m/s. A velocity of 11 m/s could lead to erosion-corrosion for carbon steel tube. However, current design
of alloy 600 spray tube should have no concern of erosion-corrosion for a velocity of 11 m/s.
Generally, the feed water ring is made of carbon steel. Therefore, junction of the carbon steel feed ring to
the alloy 600 spray tube may be subject to erosion-corrosion if velocity is high. Figure 13 shows velocity
distribution among junctions for all 33 spray tubes. As shown, the junction of Spray Tube Nos. 3 to 8 may
experience velocity ranging from 7 to 9 m/s. For carbon steel without a trace of chromium content,
erosion-corrosion may take place at the junction with velocity as high as 7 to 9 m/s. Therefore, it may be
desirable to relocate Spray Tube Nos. 3 to 8 to other locations, such as the reducer and other part of the
feed ring. To relocate to other part of the feed ring, one can use a tube pitch smaller than 4.7
o
.
Spray Tubes of Nos. 3 to 8 have the lowest discharge flow rate among 33 tubes, and yet have the highest
velocity near their junction to the feed ring. Non-uniformity in discharge flow is due to non-uniform
pressure distribution as shown in Figure 11. We have considered that all 33 discharge windows on spray
tubes are at same pressure. In reality, pressure at the discharge windows may vary, and thus amount of
non-uniformity in discharge flow can change. However, it is considered that pressure variation among 33
discharge windows is small compared to the pressure differential between the inlet and outlet of each spray
tube. Therefore, use of constant pressure for all 33 discharge windows is a good approximation. If desired,
the uncertainty of constant pressure boundary condition can be removed if we consider a fluid domain to
include water pool outside the feed ring. Such a model is to be simulated in the continued CFD analysis for
nuclear steam generator design.
















Figure 10. Schematic of Feed Water Distribution System
152.4 133.108
5.9
1
4
.
9
3
2
4
.
8
8
R
5
8
.
4
3
2
3
5
3
8
.
1
35
o
Note: Unit is cm
Z
Y
58.483 118.178
F
l
o
w

O
u
t
l
e
t
F
l
o
w

O
u
t
l
e
t
F
l
o
w

I
n
l
e
t
1
3
3
.
1
0
8
1
5
2
.
4

=
3
2
o
1 2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 33 Spray Tube No. =
Z
X
1
7
6
.
6
6
1
Flow Inlet
152.4 133.108
5.9
1
4
.
9
3
2
4
.
8
8
R
5
8
.
4
3
2
3
5
3
8
.
1
35
o
Note: Unit is cm
Z
Y
58.483 118.178
F
l
o
w

O
u
t
l
e
t
F
l
o
w

O
u
t
l
e
t
F
l
o
w

I
n
l
e
t
152.4 133.108
5.9
1
4
.
9
3
2
4
.
8
8
R
5
8
.
4
3
2
3
5
3
8
.
1
35
o
Note: Unit is cm
Z
Y
58.483 118.178
F
l
o
w

O
u
t
l
e
t
F
l
o
w

O
u
t
l
e
t
F
l
o
w

I
n
l
e
t
1
3
3
.
1
0
8
1
5
2
.
4

=
3
2
o
1 2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 33 Spray Tube No. =
Z
X
1
7
6
.
6
6
1
Flow Inlet
1
3
3
.
1
0
8
1
5
2
.
4

=
3
2
o

=
3
2
o
1 2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 33 Spray Tube No. =
Z
X
1
7
6
.
6
6
1
Flow Inlet

Figure 11. Pressure Distribution on the Inner Wall of Feed Water Distribution System


Figure 12. Velocity Vector on Symmetry Plane and Spray Tube Outlets, and Velocity
Contours

Figure 13. Velocity on a Plane Normal to Spray Tubes and 1.6 cm below Top of the Feed
Ring

Discussions
CFX-5 offers a wide range of capability in simulating fluid flow. Four modules presented above of course
cover just a small area of the CFX-5 capability. Modules 1, 2 and 4 consider single phase flow without
heat transfer, and Module 3 again deals only single phase flow, but with energy transfer due to hot and cold
water mixing. All four modules are models at important areas in the PWR steam generator, the modules
demonstrate that CFX-5 can be used to verify and optimize the design. These capabilities are important in
view that flow tests are now generally out of the reach.
Steam generator involves a wide range of thermal and hydraulics. Four modules will not cover the whole
range. For example, there are water and steam flow that are of two-phase. A simulation of two-phase flow
through the opening of the tube support plate was made at Rensselaer Polytechnic Institute (Ref 5) via a
contract from Westinghouse, and not included in this paper. Module 1 demonstrates the flexibility of the
CFX-5 code in simulating tube bundle flow through the use of porous media. Module 2 also involves the
use of porous media for the tortuous passage through the moisture separation device. The porous media
modeling works well for both cases. As of now, Module 3 considered only water flow, and results of
water flow are used together with the empirical correlation of sludge particle settlement. Module 3 for the
sludge collector can include sludge particles with water flow, and the amount of settlement of the sludge
particle could be directly estimated without using the empirical correlation. Continued module
development will include simulation of two-phase flow, such as steam and water flow, and water with solid
particle in the above mentioned sludge collector. Module 4 encountered certain difficulty in building the
solid. The code cannot accept the projection of the half circle arc from the upstream pipe into the Tee
pipe when both pipes have equal diameter. However at the advice of the CFX Technical Center, a
reduction of the upstream pipe diameter from 38.100 cm to 38.092 cm solves the difficulty. Compared to
Module 3, solution of Model 4 is relatively easier, and results of the pipe flow like Module 4 offers a lot for
properly locating the layout of the spray tubes.
CFX-5 provides excellent means to post processing the results of the CFD calculation. For example,
graphical representation itself can be adequate to confirm the design requirement. Figure 9 is such an
example, temperature distribution on wall of various components clearly depicts that the sludge collector
draws just the recirculated water, not the feed water. As the recirculated water has a higher concentration
of sludge particles than the feed water, thus a collector will be more efficient to draw the recirculated water
only. Module 2 demonstrates again that CFX-5s graphical option provides a quick estimate of range of
steam transport time through a complicated, 3-D domain. If the numeric is important the user-defined
surface can serve the user well. For instance, we defined user surfaces through eight inlet and eight outlet
holes on top of the collector, and obtained flow rates through them.
Conclusions
It appears practical and useful to divide the whole steam generator into modules when adapting CFX-5 for
CFD analysis. The CFX-5 CFD code apparently offers a wide spectrum of capability in evaluating thermal
and hydraulics of engineering equipments. Current paper emphasizes in one aspect: simple, practical
capability as a CFD analysis tool. The presented modules of four have successfully demonstrated the
capability of the CFX-5 in verifying or optimizing the component designs of the PWR steam generator.
Acknowledgements
The author would like to acknowledge that the presented Modules 1, 3 and 4 were supported through two
contracts granted by Mitsubishi Heavy Industries, Ltd for design and analysis of Tsuruga Nuclear Power
Plant Units 3 and 4 in Japan. In addition, excellent support from the ANSYS CFX Technical Center is
gratefully acknowledged.
References
1) Keeton, L. W., and Singhal, A. K., ATHOS3: A Computer Program for Thermal-Hydraulic
Analysis of Steam generators, EPRI NP-4604-CCM, Electric Power Research Institute, July
1986.
2) Kreith, F., Principles of Heat Transfer, 3
rd
Ed., Intext Educational Publishers, New York, p.482.
3) Kays, W. M., Convective Heat and Mass Transfer, McGraw-Hill, New York, 1966, p. 73.
4) Mi, J., Pordal, H., and Svihla, C. K., Calculating Residence time in CFX-5, ANSYS CFX, Feb.
8, 2001.
5) Podowski, M.Z., Antal, S. and Hu, M.H., CFD Analysis of Two-Phase Flow Around Tube
Support Plates in U-Tube Steam Generators, Proc. International Conference on Industrial
Applications of Two-Phase flow, Milan, Italy, October 1998.