!

"#$%&'
)*
+,-./012 3.452016.
78 ! A uniIorm magnetic Iield oI magnitude 2000 G is parallel to the x axis. A square coil oI side 5 cm has a
single turn and makes an angle ! with the z axis as shown in Figure 30-28. Find the magnetic Ilux through the
coil when (a) ! 0, (b) ! 30, (c) ! 60, and (d) ! 90.
(a), (b), (c), (d) "m
BA cos ! (a) "m
2#10
1
#
25#10
4
Wb 5#10
4
Wb 0.5 mWb;
(b) "m
0.433 mWb; (c) "m
0.25 mWb; (d) "m
0
9 ! A circular coil has 25 turns and a radius oI 5 cm. It is at the equator, where the earth's magnetic Iield is 0.7
G north. Find the magnetic Ilux through the coil when its plane is (a) horizontal, (b) vertical with its axis
pointing north, (c) vertical with its axis pointing east, and (d) vertical with its axis making an angle oI 30 with
north.
(a), (b), (c) Use Equ. 30-3 (a) "m
|(25#7#10
5
#$#25#10
4
) cos 90| Wb 0
(b) "m
(1.37#10
5
cos 0) Wb 1.37#10
5
Wb
(c) "m
(1.37#10
5
cos 30) Wb 1.19#10
5
Wb
) ! A magnetic Iield oI 1.2 T is perpendicular to a square coil oI 14 turns. The length oI each side oI the coil is
5 cm. (a) Find the magnetic Ilux through the coil. (b) Find the magnetic Ilux through the coil iI the magnetic
Iield makes an angle oI 60 with the normal to the plane oI the coil.
(a), (b) Use Equ. 30-3 (a) "m
(14#25#10
4
#1.2) Wb 0.042 Wb
(b) "m
(0.042 cos 60) Wb 0.021 Wb
: ! A circular coil oI radius 3.0 cm has its plane perpendicular to a magnetic Iield oI 400 G. (a) What is the
magnetic Ilux through the coil iI the coil has 75 turns? (b) How many turns must the coil have Ior the Ilux to be
0.015 Wb?
(a), (b) Use Equ. 30-3 (a) "m
(75#$#9#10
4
#4#10
2
) Wb 8.48 mWb
(b) N 75(15/8.48) 133
;8 ! A uniIorm magnetic Iield B is perpendicular to the base oI a hemisphere oI radius R. Calculate the
magnetic Ilux through the spherical surIace oI the hemisphere.
Note that "m
through the base must also penetrate the spherical surIace. Thus, "m
$R
2
B.
< !! Find the magnetic Ilux through a solenoid oI length 25 cm, radius 1 cm, and 400 turns that carries a current
Chapter 30 Magnetic Induction
oI 3 A.
Use Equs. 29-9 and 30-3; "m
0
N
2
AI/L "m
7.58#10
4
Wb
= !! Work Problem 6 Ior an 800-turn solenoid oI length 30 cm, and radius 2 cm, carrying a current oI 2 A.
Use Equs. 29-9 and 30-3; "m
0
N
2
AI/L "m
6.74#10
3
Wb
> !! A circular coil oI 15 turns oI radius 4 cm is in a uniIorm magnetic Iield oI 4000 G in the positive x
direction. Find the Ilux through the coil when the unit vector perpendicular to the plane oI the coil is (a) n i,
(b) n j, (c) n (i j)/ 2 , (d) n k, and (e) n 0.6i 0.8j.
(a), (b), (c), (d), (e) Use Equ. 30-1 with B 0.4 T i (a) NA 0.0704 m
2
; "m
0.0302 Wb. (b) "m
0
(c) Wb 0.0213 Wb 2 / 0.0302
m
" . (d) "m
0
(e) "m
0.0169 Wb
?8 !! A solenoid has n turns per unit length, radius R
1
, and carries a current I. (a) A large circular loop oI radius
R
2
~ R
1
and N turns encircles the solenoid at a point Iar away Irom the ends oI the solenoid. Find the magnetic
Ilux through the loop. (b) A small circular loop oI N turns and radius R
3
R
1
is completely inside the solenoid,
Iar Irom its ends, with its axis parallel to that oI the solenoid. Find the magnetic Ilux through this small loop.
(a) B Ior R ~ R
1
0; so "m
NBA 0
nIN$R
1
2
.
(b) Now A $R
3
2
, so "m
0
nIN$R
3
2
.
7* !! A long, straight wire carries a current I. A rectangular loop with two sides parallel to the straight wire has
sides a and b with its near side a distance d Irom the straight wire, as shown in Figure 30-29. (a) Compute the
magnetic Ilux through the rectangular loop. (Hint: Calculate the Ilux through a strip oI area dA b dx and
integrate Irom x d to x d a.) (b) Evaluate your answer Ior a 5 cm, b 10 cm, d 2 cm, and I 20 A.
(a) 1. Find d"m
(x) BdA; use Equ. 29-12
2. Integrate d"m
(x) Irom d to (d + a)
(b) Evaluate "m
d"m
(x) (0
/2$)Ibdx/x
"m
(0
Ib/2$)ln|(d + a)/d|
"m
4#10
7
#ln(7/2) Wb 5.01#10
7
Wb
77 !!! A long, cylindrical conductor oI radius R carries a current I that is uniIormly distributed over its cross-
sectional area. Find the magnetic Ilux per unit length through the area indicated in Figure 30-30.
At r R, B 0
Ir/2$R
2
(see Problem 29-49). The Ilux d"m
through an area Ldr is BLdr, and the total Ilux
through the area A is obtained by integrating d"m
Irom r 0 to r R. One obtains "m
0
LI/4$, and the Ilux
per unit length is then "m
0
I/4$.
79 !!! A rectangular coil in the plane oI the page has dimensions a and b. A long wire that carries a current I is
placed directly above the coil (Figure 30-31). (a) Obtain an expression Ior the magnetic Ilux through the coil as
a Iunction oI x Ior 0 % x % 2b. (b) For what value oI x is Ilux through the coil a maximum? For what value oI x
is the Ilux a minimum?
(a) Note that Ior 0 % x % b, B is symmetric about the wire, into the paper Ior the region below the wire and out
oI the paper Ior the region above the wire. Clearly, the net Ilux is zero Ior the area 2(b x)a. We can now use
the result oI Problem 30-10 to Iind the Ilux through the remaining area oI the rectangle. Thus, Ior 0 % x % b, we
Iind "m
(0
Ia/2$)ln|x/(b x)|. For x & b, we Iind "m
(0
Ia/2$)ln|(x + b)/x).
(b) From the expressions derived in (a) we see that '"m' ( ) as x ( 0. This is the result oI assuming a wire
oI inIinitesimal radius; Ior R 0, Equ. 29-12 diverges. The Ilux is a minimum ("m
0) Ior x b/2, as expected
Chapter 30 Magnetic Induction
Irom symmetry.
7)8 ! A conducting loop lies in the plane oI this page and carries a clockwise induced current. Which oI the
Iollowing statements could be true?
(a) A constant magnetic Iield is directed into the page.
(b) A constant magnetic Iield is directed out oI the page.
(c) An increasing magnetic Iield is directed into the page.
(d) A decreasing magnetic Iield is directed into the page.
(e) A decreasing magnetic Iield is directed out oI the page.
(d)
7: ! A uniIorm magnetic Iield B is established perpendicular to the plane oI a loop oI radius 5.0 cm, resistance
0.4 *, and negligible selI-inductance. The magnitude oI B is increasing at a rate oI 40 mT/s. Find (a) the
induced emI in the loop, (b) the induced current in the loop, and (c) the rate oI Joule heating in the loop.
(a) Use Equs. 30-3 and 30-5; '
E
' A dB/dt
(b) I E/R
(c) P I
2
R
'
E
' (0.04#$#25#10
4
) V 0.314 mV
I 0.785 mA
P 0.247 W
7; ! The Ilux through a loop is given by "m
(t
2
4t)#10
1
Wb, where t is in seconds. (a) Find the induced emI
E as a Iunction oI time. (b) Find both "m
and E at t 0, t 2 s, t 4 s, and t 6 s.
(a) Use Equ. 30-5
(b) Evaluate E and "m
Ior t 0, 2, 4, and 6 s
E (0.2t 0.4) V
E(0) 0.4 V; E(2) 0; E(4) 0.4 V; E(6) 0.8 V
"m
(0) 0; "m
(2) 0.4 Wb; "m
(4) 0; "m
(6) 1.2 Wb
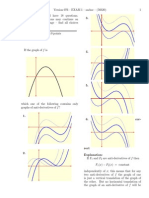
7< ! (a) For the Ilux given in Problem 15, sketch graphs oI "m
and E versus t. (b) At what time is the Ilux
minimum? What is the emI at this time? (c) At what times is the Ilux zero? What is the emI at these times?
(a) The graphs oI the Ilux, ",and induced emI, E,
are shown in the adjacent Iigure. The solid curve
represents ", the dashed curve represents E.
(b) The Ilux is a minimum at t 2 s; at that instant
E 0.
(c) The Ilux is zero at t 0 and t 4 s; at these
times,
E 0.4 V and 0.4 V, respectively.

7=8 ! The magnetic Iield in Problem 4 is steadily reduced to zero in 0.8 s. What is the magnitude oI the emI
induced in the coil oI part (b)?
E d"m
/dt
'
E
' 0.015/0.8 V 18.75 mV

7> ! A solenoid oI length 25 cm and radius 0.8 cm with 400 turns is in an external magnetic Iield oI 600 G that
makes an angle oI 50 with the axis oI the solenoid. (a) Find the magnetic Ilux through the solenoid. (b) Find
the magnitude oI the emI induced in the solenoid iI the external magnetic Iield is reduced to zero in 1.4 s.
(a) Use Equ. 30-3
(b) Use Equ. 30-5

"m
(400#0.06#$#64#10
6
#cos 50) Wb 3.10 mWb
E (3.10#10
3
/1.4) V 2.21 Mv
Chapter 30 Magnetic Induction

7? !! A 100-turn circular coil has a diameter oI 2.0 cm and resistance oI 50 *. The plane oI the coil is
perpendicular to a uniIorm magnetic Iield oI magnitude 1.0 T. The direction oI the Iield is suddenly reversed.
(a) Find the total charge that passes through the coil. II the reversal takes 0.1 s, Iind (b) the average current in
the coil and (c) the average emI in the coil.
(a) 1. Use Equ. 30-5, E IR, and I +Q/+t
2. Evaluate "m
and +Q
(b) I
av
+Q/+t
(c) E
av
I
av
R

+"m
2"m
IR+t R+Q; +Q 2"m
/R

"m
31.4 mWb; +Q 1.26 mC
I
av
12.6 mA
E
av
628 mV

9* !! At the equator, a 1000-turn coil with a cross-sectional area oI 300 cm
2
and a resistance oI 15.0 * is aligned
with its plane perpendicular to the earth's magnetic Iield oI 0.7 G. II the coil is Ilipped over, how much charge
Ilows through it?

+Q 2"m
/R (see Problem 3019); +Q 2NBA/R
+Q 0.28 mC

978 !! A circular coil oI 300 turns and radius 5.0 cm is connected to a current integrator. The total resistance oI
the circuit is 20 *. The plane oI the coil is originally aligned perpendicular to the earth's magnetic Iield at some
point. When the coil is rotated through 90, the charge that passes through the current integrator is measured to
be 9.4 C. Calculate the magnitude oI the earth's magnetic Iield at that point.
1. Relate the Ilux change to the charge
2. +"m
NBA; B QR/NA QR/N$r
2
E +"m
/+t; I E/R; Q I+t +"m
/R
B 79.8 T

99 !! An elastic circular conducting loop is expanding at a constant rate so that its radius is given by R R
0
vt.
The loop is in a region oI constant magnetic Iield perpendicular to the loop. What is the emI generated in the
expanding loop? Neglect possible eIIects oI selI-inductance.
The Ilux is given by "m
$R
2
B $(R
0
vt)
2
B. Thus E (d"m
/dt) 2$vB(R
0
vt).
9) !! The wire in Problem 12 is placed at x b/4. (a) Obtain an expression Ior the emI induced in the coil iI the
current varies with time according to I 2t. (b) II a 1.5 m and b 2.5 m, what should be the resistance oI the
coil so that the induced current is 0.1 A? What is the direction oI this current?
(a) From Problem 30-12, "m
(0
Ia/2$)ln(1/3) 1.100
Ia/2$. Thus E 1.100
a/$.
(b) R E/I 1.100
a/$I; solve Ior R R 6.6 *; the current is counterclockwise.

9: !! Repeat Problem 23 iI the wire is placed at x b/3.
(a) For x b/3, ln|x/(x b)| ln(1/2) 0.693. Then E 0.6930
a/$.
(b) Now R |6.6(0.693/1.10)| * 4.16 *; the current is again counterclockwise.
9;8 ! Give the direction oI the induced current in the circuit on the right in Figure 30-32 when the resistance in
the circuit on the leIt is suddenly (a) increased and (b) decreased.
Note that when R is constant, B in the loop to the right points out oI the paper.
(a) II R increases, I decreases and so does B. By Lenz`s law, the induced current is counterclockwise.
(b) Conversely, iI R decreases, the induced current is clockwise.
9< !! The two circular loops in Figure 30-33 have their planes parallel to each other. As viewed Irom A toward
B, there is a counterclockwise current in loop A. Give the direction oI the current in loop B and state whether
Chapter 30 Magnetic Induction
the loops attract or repel each other iI the current in loop A is (a) increasing and (b) decreasing.
(a) Current in B is clockwise; loops repel one another.
(b) Current in B is counterclockwise; loops attract one another.
9= !! A bar magnet moves with constant velocity along the axis oI a loop as shown in Figure 30-34. (a) Make a
qualitative graph oI the Ilux "m
through the loop as a Iunction oI time. Indicate the time t
1
when the magnet is
halIway through the loop. (b) Sketch a graph oI the current I in the loop versus time, choosing I to be positive
when it is counterclockwise as viewed Irom the leIt.
(a), (b) The adjacent Iigure shows the Ilux and
induced current as a Iunction oI time as the bar
magnet passes through the coil. When the center oI
the magnet passes through the plane oI the coil d"m
/dt 0, and the current is zero. In the Iigure, the solid
curve represents the Ilux, and the dashed curve
represents the current.


9> !! A bar magnet is mounted on the end oI a coiled spring in such a way that it moves with simple harmonic
motion along the axis oI a loop as shown in Figure 30-35. (a) Make a qualitative graph oI the Ilux "m
through
the loop as a Iunction oI time. Indicate the time t
1
when the magnet is halIway through the loop. (b) Sketch the
current I in the loop versus time, choosing I to be positive when it is counterclockwise as viewed Irom above.
(a), (b) The adjacent Iigure shows the Ilux, "m
, and
the induced current in the loop as a Iunction oI time.
The Ilux is shown as the solid curve, thecurrent as
the dashed curve. The times when the magnet is
halIway through the loop is indicated. At those times
the Ilux is a maximum and the current is zero.


9?8 ! A rod 30 cm long moves at 8 m/s in a plane perpendicular to a magnetic Iield oI 500 G. The velocity oI the
rod is perpendicular to its length. Find (a) the magnetic Iorce on an electron in the rod, (b) the electrostatic
Iield E in the rod, and (c) the potential diIIerence V between the ends oI the rod.
(a) F qv
# ## #
B
(b) E v
# ## #
B
(c) V E!
F 1.6#10
19
#8#5#10
2
N 6.4#10
20
N
E 0.4 V/m
V 0.12 V

)* ! Find the speed oI the rod in Problem 29 iI the potential diIIerence between the ends is 6 V.
V , v; use the result oI Problem 29 v (6/0.12)(8 m/s) 400 m/s

Chapter 30 Magnetic Induction
)7 ! In Figure 30-14, let B be 0.8 T, v 10.0 m/s, ! 20 cm, and R 2 *. Find (a) the induced emI in the
circuit, (b) the current in the circuit, and (c) the Iorce needed to move the rod with constant velocity assuming
negligible Iriction. Find (d) the power input by the Iorce Iound in part (c), and (e) the rate oI Joule heat
production I
2
R.
(a) Use Equ. 30-6
(b) I E/R; use Lenz`s law
(c) Use Equ. 28-5; F BI !
(d) P Fv
(e) P I
2
R
E (0.8#0.2#10.0) V 1.6 V
I 0.8 A, counterclockwise
F 0.128 N
P 1.28 W
P 1.28 W

)9 ! Work Problem 31 Ior B 1.5 T, v 6 m/s, ! 40 cm, and R 1.2 *.
Repeating the procedure oI the previous problem one obtains:
(a) E 3.6 V (b) I 3.0 A (c) F 1.8 N (d) P 10.8 W (e) P 10.8 W
))8 !! A 10-cm by 5-cm rectangular loop with resistance 2.5 * is pulled through a region oI uniIorm magnetic
Iield B 1.7 T (Figure 30-36) with constant speed v 2.4 cm/s. The Iront oI the loop enters the region oI the
magnetic Iield at time t 0. (a) Find and graph the Ilux through the loop as a Iunction oI time. (b) Find and
graph the induced emI and the current in the loop as Iunctions oI time. Neglect any selI-inductance oI the loop
and extend your graphs Irom t 0 to t 16 s.
(a) For 0 t 4.17 s, "m
0.05Bvt 2.04#10
3
t;
Ior 4.17 s t 8.33 s, "m
8.51 mWb;
Ior 8.33 s t 12.5 s, "m
8.51#10
3
(t 8.33);
Ior t ~ 12.5 s, "m
0
The graph oI "m
(t) is shown on the right. Here "m
is in mWb, t in s.


(b) E (d"m
/dt); Ior 0 t 4.17 s, E 2.04 mV
Ior 4.17 s t 8.33 s, E 0;
Ior 8.33 s t 12.5 s, E 2.04 mV;
Ior t ~ 12.5 s, E 0.
The graph oI E(t) is shown on the right. Here E
is in mV and t in s.
The graph oI the current is identical to that oI E
with the ordinate scale changed to I
max
0.8 mA.


): !! A uniIorm magnetic Iield oI magnitude 1.2 T is in the z direction. A conducting rod oI length 15 cm lies
parallel to the y axis and oscillates in the x direction with displacement given by x (2 cm) cos 120$t. What is
the emI induced in the rod?
Use Equ. 30-6 and v dx/dt; E B! A- sin(-t) E |1.36 sin (120$t)| V

Chapter 30 Magnetic Induction
); !! In Figure 30-37, the rod has a resistance R and the rails are horizontal and have negligible resistance. A
battery oI emI E and negligible internal resistance is connected between points a and b such that the current in
the rod is downward. The rod is placed at rest at t 0. (a) Find the Iorce on the rod as a Iunction oI the speed v
and write Newton's second law Ior the rod when it has speed v. (b) Show that the rod moves at a terminal speed
and Iind an expression Ior it. (c) What is the current when the rod will approach its terminal speed?
(a) The net emI that drives a current in this circuit is the emI oI the battery minus the induced emI in the rod as
a result oI its motion. Thus, I (E B! v)/R. The Iorce on the rod due to this current is F BI ! . Newton`s
equation oI motion is thereIore ma (B! /R)(E B! v).
(b) Note that a diminishes as v increases and becomes zero when v v
t
E/B! , where v
t
is the terminal
speed.
(c) It Iollows Irom the expression Ior I given above that when v v
t
, I 0.
)< !! In Example 30-8, Iind the total energy dissipated in the resistance and show that it is equal to
2
1
mv
0
2
.
The power dissipated is P I
2
R (B! v)
2
/R, where v v
0
exp(-B
2
!
2
t/mR). The total energy dissipated as the
rod comes to rest is obtained by integrating dE P dt. Thus,

2
0
0
2 2
0
2 2
2
1
2
0
2 2
mv dt e
R
v B
E
mR
v B
= =
.
)
/
!
!
)=8 !! Find the total distance traveled by the rod in Example 30-8.
Note that v dx/dt v
0
e
Ct
, where C B
2
!
2
/mR. Integrating the diIIerential equation gives x
.
)
/
=
0
0 0
/ C V dt e v
Ct
.
The distance traveled is v
0
mR/B
2
!
2
.
)> !! In Figure 30-37, the rod has a resistance R and the rails have negligible resistance. A capacitor with charge
Q
0
and capacitance C is connected between points a and b such that the current in the rod is downward. The
rod is placed at rest at t 0. (a) Write the equation oI motion Ior the rod on the rails. (b) Show that the terminal
speed oI the rod down the rails is related to the Iinal charge on the capacitor.
(a) In this case, the current is given by I (Q/C B! v)/R. The current is due to the discharge oI the capacitor;
consequently, I dQ/dt. The acceleration is also proportional to the current through F BI ! ma m dv/dt.
So dQ/dt (m/B! ) dv/dt, or dQ (m/B! ) dv. This is readily integrated; with Q Q
0
Ior v 0 one obtains
Q Q
0
mv/B! . Thus the equation oI motion is
v
R m

B
+
C R
1

C R m
Q B
= v B
C
) v/B (m Q

R m
B
=
m
I B
=
dt
dv
2 2
0 0
0
0
1
2
3
3
4
5
/
0
0
1
2
3
3
4
5
/
/
!
!
!
! ! !
(b) At the terminal speed, F 0 and thereIore I 0. Thus, Q
I
/C B!

v
t
, or v
t
Q
I
/CB! .
)? !! In Figure 30-38, a conducting rod oI mass m and negligible resistance is Iree to slide without Iriction along
two parallel rails oI negligible resistance separated by a distance ! and connected by a resistance R. The rails
are attached to a long inclined plane that makes an angle ! with the horizontal. There is a magnetic Iield B
directed upward. (a) Show that there is a retarding Iorce directed up the incline given by
R. / )
B
( = F
2
!
cos
v
2 2
!
(b) Show that the terminal speed oI the rod is ).
B
( / ) mgR
v
2
! !
cos
sin (
2 2
t !
(a) Here, only the horizontal component oI v produces an induced emI; Irom Equ. 30-6, E B! v cos !, and
the current in the circuit is then I (B! v/R) cos !. The Iorce due to the interaction oI the current I with the
magnetic Iield B is given by F I !
# ## #
B, which points in the horizontal direction and has the magnitude F
(B
2
!
2
v/R) cos !. However, only the component oI F along the inclined plane contributes to the retarding Iorce.
Chapter 30 Magnetic Induction
So F
ret
(B
2
!
2
v/R) cos
2
!.
(b) From Newton`s law, dv/dt g sin ! F
ret
/m. At the terminal velocity, v
t
, dv/dt 0. Solving Ior v
t
one Iinds
v
t
(mgR sin !)/(B
2
!
2
cos
2
!).
:* !! A simple pendulum has a wire oI length ! supporting a metal ball oI mass m. The wire has negligible mass
and moves in a uniIorm horizontal magnetic Iield B. This pendulum executes simple harmonic motion having
angular amplitude !0
. What is the emI generated along the wire?
Since the pendulum moves with SHM, !(t) !0
cos -t, where ! g/ = - . Consider a segment dr along the wire
a distance r Irom the pivot. The emI dE induced in this segment due to the motion oI the wire is given by
dE Br(d!/dt)dr Br-!0
sin -t dr.Integrating Irom r 0 to r ! gives E 1/2B!
2
-!0
sin -t.
:78 !! A wire lies along the z axis and carries current I 20 A in the positive z direction. A small conducting
sphere oI radius R 2 cm is initially at rest on the y axis at a distance h 45 m above the wire. The sphere is
dropped at time t 0. (a) What is the electric Iield at the center oI the sphere at t 3 s? Assume that the only
magnetic Iield is that produced by the wire. (b) What is the voltage across the sphere at t 3 s?
(a) 1. Find B(y); use Equ. 29-12
2. Find the velocity oI the sphere at t 3 s
3. Find y at t 3 s; y h 1/2gt
2
and B
4. Find E v
# ## #
B
(b) V 2RE
B 200
/2$y i (4#10
6
/y) T i
v gt j 29.4 m/s j
y 0.855 m; B 1.17#10
6
T i
E 0.138 mV/m k
V 5.50 V

:9 !! In Figure 30-38, let ! 30, m 0.4 kg, ! 15 m, and R 2.0 *. The rod starts Irom rest at the top oI the
inclined plane at t 0. The rails have negligible resistance. There is a constant, vertically directed magnetic
Iield oI magnitude B 1.2 T. (a) Find the emI induced in the rod as a Iunction oI its velocity down the rails. (b)
Write Newton's law oI motion Ior the rod; show that the rod will approach a terminal speed and determine its
value.
(a) E B! v cos ! (see Problem 30-39)
(b) dv/dt g sin ! (B
2
!
2
v/Rm)cos
2
!
E (1.56v) V
Dv/dt 4.905 3.038v; v
t
1.61 m/s

:) !! When the rod oI Problem 42 moves at its terminal speed, what is the power dissipated in the resistor? What
is the rate oI change oI the potential energy oI the rod?
P I
2
R; I (B! v
t
/R) cos ! (see Problem 30-39)
U mgy; dU/dt mgv
t
sin !
P 3.16 W
dU/dt 3.16 W

:: !!! A solid conducting cylinder oI radius 0.1 m and mass oI 4 kg rests on horizontal conducting rails (Figure
30-39). The rails, separated by a distance a 0.4 m, have a rough surIace so the cylinder rolls rather than
slides. A 12-V battery is connected to the rails as shown. The only signiIicant resistance in the circuit is the
contact resistance oI 6 * between the cylinder and rails. The system is in a uniIorm vertical magnetic Iield. The
cylinder is initially at rest next to the battery. (a) What must be the magnitude and direction oI B so that the
cylinder has an initial acceleration oI 0.1 m/s
2
to the right? (b) Find the Iorce on the cylinder as a Iunction oI its
speed v. (c) Find the terminal velocity oI the cylinder. (d) What is the kinetic energy oI the cylinder when it
has reached its terminal velocity? (Neglect the magnetic Iield due to the current in the batteryrailscylinder
loop and assume that the current density in the cylinder is uniIorm.)
Since the current through the rod is uniIormly distributed, we may treat the current as though it were
Chapter 30 Magnetic Induction
concentrated at the center oI the rod.
(a) 1. Write the equations oI motion. Let F
I
be the
Iriction Iorce, and I
m
the rod`s moment oI inertia.
2. Solve Ior B with dv/dt 0.1 m/s
2
and I E/R
(b) 1. Write an expression Ior I
2. Write F
net
in terms oI the constants and v
3. Write the equation oI motion
4. Try )
v
= v(t)
e
(1
t/
t
6 /
/ 0 with v
t
E/Ba
5. Substitute numerical values
(c) v
t
E/Ba
(d) K 1/2mv
t
2
1/2I
m-t
2
3mv
t
2
/4
F
net
BIa F
I
m dv/dt mr d-/dt; F
I
r I
m
d-/dt;
r d-/dt (BIa)/(m + I
m
/r2) 2BIa/3m dv/dt
B 0.75 T, pointing downward
I (E Bav)/R
F
net
(Ba/R)(E Bav) 1/2m dv/dt m dv/dt
dv/dt 2BaE/3mR (2B
2
a
2
/3mR)v
Solution is correct with 6 3mR/2B
2
a
2
)
e
(1 40 = v(t)
t/400 /
/ m/s
v
t
40 m/s
K 4800 J

:;8 !!! A rod oI length ! is perpendicular to a long wire carrying current I, as shown in Figure 30-40. The near end
oI the rod is a distance d away Irom the wire. The rod moves with a speed v in the direction oI the current I. (a)
Show that the potential diIIerence between the ends oI the rod is given by

d
+ d
v = V
!
ln
2
I
0
$

(b) Use Faraday's law to obtain this result by considering the Ilux through a rectangular area A ! vt swept out
by the rod.
(a) Consider a small segment oI the rod oI length dx. The induced Iield is dE B(x)v dx, where B(x) 0
I/2$x.
Thus,
. .
+ +
0
1
2
3
4
5 +
= = =
! !
!
d
d
d
d
d
d Iv
x
Iv
Edx V n 1
2 2
0 0
$

.
(b) Again, consider a segment dx. d"m
B dA B vt dx (0
Iv/2$x)t dx. Except Ior the Iactor t, the integrand
is the same as beIore; hence

"m
0
1
2
3
4
5
d
+ d

2
t v I
0
!
ln
$

. The induced emI is E d"m

/dt 0
1
2
3
4
5
d
+ d

2
v I
0
!
ln
$

.

:< !!! The loop in Problem 10 moves away Irom the wire with a constant speed v. At time t 0, the leIt side oI
the loop is a distance d Irom the long straight wire. (a) Compute the emI in the loop by computing the motional
emI in each segment oI the loop that is parallel to the long wire. Explain why you can neglect the emI in the
segments that are perpendicular to the wire. (b) Compute the emI in the loop by Iirst computing the Ilux
through the loop as a Iunction oI time and then using E -d"m
/dt and compare your answer with that obtained
in part (a).
(a) The motion oI the segments perpendicular to the long wire does not change the Ilux through the rectangular
loop. Consequently, these segments do not contribute to the induced emI.
1. E vBb (Equ. 30-6); B 2#10
7
I/R (Equ. 29-
12); note that the emI`s in both wires point up and
thereIore oppose one another.
(b) 1. Generalize the result oI Problem 3010
2. E (d"m
/dt)
For the near wire, E
1
2#10
7
Ibv/(d + vt); Ior the Iar
wire, E
2
2#10
7
Ibv/(d + a + vt). So the total emI is
E 2#10
7
Ibv|1/(d + vt) 1/(d + a + vt)|

"m
(2#10
7
Ib) ln|(d + a + vt)/(d + vt)|
E 2#10
7
Ibv|1/(d + vt) 1/(d + a + vt)|

:= !!! A conducting rod oI length ! rotates at constant angular velocity about one end, in a plane perpendicular to
Chapter 30 Magnetic Induction
a uniIorm magnetic Iield B (Figure 30-41). (a) Show that the magnetic Iorce on a charge q at a distance r Irom
the pivot is Bqr-. (b) Show that the potential diIIerence between the ends oI the rod is
!
2
2
1
B = V - . (c) Draw
any radial line in the plane Irom which to measure ! -t. Show that the area oI the pie-shaped region between
the reIerence line and the rod is A
2
1
!
2
!. Compute the Ilux through this area, and show that E
2
1
B-!
2
Iollows when Faraday's law is applied to this area.
(a) We have F qv
# ## #
B. Here v and B are at right angles, and v r-. So F qBr-.
(b) We can use Equ. 30-6 to Iind dE Br- dr. Integrating Irom r 0 to r ! one obtains E 1/2B-!
2
.
(c) For any value oI !, the area dA between r and r dr is r! dr. Integrating Irom r 0 to r ! , one Iinds
A 1/2 !
2
!. The Ilux through this area is "m
BA 1/2B!
2
!, and '
E
' d"m
/dt 1/2B!
2
-.
:> ! How would the selI-inductance oI a solenoid be changed iI (a) the same length oI wire were wound onto a
cylinder oI the same diameter but twice the length; (b) twice as much wire were wound onto the same cylinder;
and (c) the same length oI wire were wound onto a cylinder oI the same length but twice the diameter?
(a) L is given by Equ. 30-9. Since the diameter does not change, the number oI turns and the area A remain
constant. However, n
2
is diminished by a Iactor oI 4 and ! is increased by a Iactor oI 2. Thus L is reduced by a
Iactor oI 2.
(b) Using twice as much wire and making no other change, n
2
and L are increased by a Iactor oI 4.
(c) With twice the diameter, n
2
is reduced by a Iactor oI 4, but A is increased by the same Iactor; L is
unchanged.
:?8 ! A coil with a selI-inductance oI 8.0 H carries a current oI 3 A that is changing at a rate oI 200 A/s. Find (a)
the magnetic Ilux through the coil and (b) the induced emI in the coil.
(a) "m
LI; I (3 200t) A
(b) E -L(dI/dt)

"m
24 1600t Wb
E 1600 V

;* ! A coil with selI-inductance L carries a current I, given by I I
0
sin 2$ft. Find and graph the Ilux "m
and the
selI-induced emI as Iunctions oI time.
By deIinition, "m
LI LI
0
sin 2$f
0
t and the induced
emI E L dI/dt 2$fLI
0
cos 2$ft. The two
quantities are shown in the Iigures. The maximum
value oI the Ilux is LI
0
; the maximum value oI the
induced emI is 2$fLI
0
.


Chapter 30 Magnetic Induction

;7 !! A solenoid has a length oI 25 cm, a radius oI 1 cm, and 400 turns, and carries a 3-A current. Find (a) B on
the axis at the center oI the solenoid; (b) the Ilux through the solenoid, assuming B to be uniIorm; (c) the
selI-inductance oI the solenoid; and (d) the induced emI in the solenoid when the current changes at 150 A/s.
(a) Use Equ. 29-9
(b) "m
NBA (Equ. 30-3)
(c) L "m
/I (Equ. 30-7)
(d) Use Equ. 30-10
B (4$#10
7
#1600#3) T 6.03 mT

"m
7.58#10
4
Wb
L 0.253 mH

'
E
' 37.9 mV

;9 !! Two solenoids oI radii 2 cm and 5 cm are coaxial. They are each 25 cm long and have 300 and 1000 turns,
respectively. Find their mutual inductance.
Use Equ. 30-13 n
1
4000 m
1
, n
2
1200 m
1
; M 1.89 mH

;)8 !! A long, insulated wire with a resistance oI 18 */m is to be used to construct a resistor. First, the wire is
bent in halI, and then the doubled wire is wound in a cylindrical Iorm as shown in Figure 30-42. The diameter
oI the cylindrical Iorm is 2 cm, its length is 25 cm, and the total length oI wire is 9 m. Find the resistance and
inductance oI this wire-wound resistor.
Note that the current in the two parts oI the wire is in opposite directions. Consequently, the total Ilux in the coil is
zero, and the selI inductance is also zero. L 0. The length oI the wire is 9 m, so its resistance is 9#18 * 162 *.
;: !! Figure 30-43 shows two long solenoids each with 2000 turns oI wire. The outer solenoid is 20 cm long and
has a diameter oI 2 cm. The inner solenoid is 10 cm long and has a diameter oI 1 cm. Find the eIIective
inductance oI this arrangement.
1. Write the expression Ior L (see Problem 99)
2. Evaluate L
1
and L
2
using Equs. 30-9
3. Evaluate M 0
N
1
N
2
A
1
/ !
1
4. Evaluate L L
1
L
2
2M; note that Ilux oI L
1

opposes that oI L
2
; use the negative sign.
L L
1
L
2
+ 2M
L
1
0 #$#10
3
H; L
2
0 #2$#10
3
H
M 0 #$#10
3
H

L 2$#10
3
0
H 7.90 mH

;; !!! In Figure 30-44, circuit 2 has a total resistance oI 300 *. A total charge oI 2#10
4
C Ilows through the
galvanometer in circuit 2 when switch S in circuit 1 is closed. AIter a long time, the current in circuit 1 is 5 A.
What is the mutual inductance between the two coils?
1. Use KirchhoII`s law Ior the galvanometer circuit
2. Integrate each term Irom t 0 to t )
3. Solve Ior and evaluate M
M dI
1
/dt + L
2
dI
2
/dt RI
2
0
MI
1)
L
2
I
2)
RQ 0; I
2)
0
M RQ/I
2)
12 mH

;< !!! Show that the inductance oI a toroid oI rectangular cross section as shown in Figure 30-45 is given by

$

2
(b/a) ln H
N
2
0
= L
where N is the total number oI turns, a is the inside radius, b is the outside radius, and H is the height oI the
toroid. From Equ. 29-17, B 0
NI/2$r. Consider a strip oI height H and width dr; the Ilux in this strip is
d"m
BHdr. Integrate d"m
Irom r a to r b. The result is "m
(0
NIH/2$) ln(b/a). This Ilux encloses N
turns, so L N"m
/I (0
N
2
H/2$) ln(b/a).
Chapter 30 Magnetic Induction
;=8 ! II the current through an inductor were doubled, the energy stored in the inductor would be (a) the same.
(b) doubled. (c) quadrupled. (d) halved. (e) quartered.
(c)

;> ! A coil with a selI-inductance oI 2.0 H and a resistance oI 12.0 * is connected across a 24-V battery oI
negligible internal resistance. (a) What is the Iinal current? (b) How much energy is stored in the inductor
when the Iinal current is attained?
(a) I
I
E/R
(b) Use Equ. 30-16
I
I
2 A
U
m
4 J

;? ! Find (a) the magnetic energy, (b) the electric energy, and (c) the total energy in a volume oI 1.0 m
3
in
which there is an electric Iield oI 10
4
V/m and a magnetic Iield oI 5000 G.
(a) u
E
1/2
70
E
2
(Equ. 25-11)
(b) u
m
1/2B
2
/0
(c) U U
E
U
m
8 U
m
U
E
4.43#10
4
J
U
m
9.95#10
4
J
U 9.95#10
4
J

<* !! In a plane electromagnetic wave such as a light wave, the magnitudes oI the electric and magnetic Iields are
related by E cB, where c 1/
7
0
0
is the speed oI light. Show that in this case the electric and the magnetic
energy densities are equal.
From Equs. 25-11 and 30-17 we have u
E
1/2
70
E
2
and u
m
1/2B
2
/0
. II E cB, then E
2
B
2
/700
and u
E
u
m
.
<78 !! A solenoid oI 2000 turns, area 4 cm
2
, and length 30 cm carries a current oI 4.0 A. (a) Calculate the
magnetic energy stored in the solenoid Irom
2
1
LI
2
. (b) Divide your answer in part (a) by the volume oI the
solenoid to Iind the magnetic energy per unit volume in the solenoid. (c) Find B in the solenoid. (d) Compute
the magnetic energy density Irom u
m
B
2
/20
, and compare your answer with your result Ior part (b).
(a) Use Equ. 30-9 to Iind L; U
m
1/2LI
2
(b) u
m
U
m
/V U
m
/A!
(c) B 0
nI 0
NI/ !
(d) u
m
B
2
/20
L 6.70 mH; U
m
53.6 mJ
u
m
447 J/m
3
B 33.5 mT
u
m
447 J/m
3
as in part (b)
<9 !! A long, cylindrical wire oI radius a 2 cm carries current I 80 A uniIormly distributed over its cross-
sectional area. Find the magnetic energy per unit length within the wire.
Consider a cylindrical annulus oI thickness dr at a radius r a. The Iield B is given by B 0
Ir/2$a
2
(see
Problem 29-49). The magnetic energy per unit length in this annulus is dU
m
(0
I
2
r
2
/8$
2
a
4
)2$r dr. To Iind the
total magnetic energy within the cylinder, integrate dU
m
Irom r 0 to r a. The result is U
m
0
I
2
/16$. Note
that the magnetic energy per unit length is independent oI the radius oI the cylinder and depends only on the
total current. Substitute numerical values. U
m
0.16 mJ/m.
<) !! A toroid oI mean radius 25 cm and circular cross section oI radius 2 cm is wound with a superconducting
wire oI length 1000 m that carries a current oI 400 A. (a) What is the number oI turns on the coil? (b) What is
the magnetic Iield at the mean radius? (c) Assuming that B is constant over the area oI the coil, calculate the
magnetic energy density and the total energy stored in the toroid.
(a) Length per turn 2$r; N L/2$r
(b) Use Equ. 29-17; here r r
mean
N 7958
B 2.55 T
Chapter 30 Magnetic Induction
(c) Use Equ. 30-17; V 8 2$
2
r
2
r
mean
; U
m
Vu
m
u
m
2.58#10
6
J/m
3
; U
m
5.09 kJ
<: ! A coil oI resistance 8.0 * and selI-inductance 4.0 H is suddenly connected across a constant potential
diIIerence oI 100 V. Let t 0 be the time oI connection, at which the current is zero. Find the current I and its
rate oI change dI/dt at times (a) t 0, (b) t 0.1 s, (c) t 0.5 s, and (d) t 1.0 s.
(a), (b), (c), (d) Use Equs. 30-21 and 30-22
and evaluate Ior t 0, 0.1 s, 0.5 s, and 1.0 s
I 12.5(1 e
t/0.5
) A; dI/dt 25e
t/0.5
A/s
t 0: I 0, dI/dt 25 A/s
t 0.1 s: I 2.27 A, dI/dt 20.5 A/s
t 0.5 s: I 7.90 A, dI/dt 9.20 A/s
t 1.0 s: I 10.8 A, dI/dt 3.38 A/s
<;8 ! The current in a coil with a selI-inductance oI 1 mH is 2.0 A at t 0, when the coil is shorted through a
resistor. The total resistance oI the coil plus the resistor is 10.0 *. Find the current aIter (a) 0.5 ms and (b) 10
ms.
(a), (b) I(t) I
0
e
(R/L)t
; R/L 10
4
s
1
(a) I(0.5 ms) 13.5 mA (b) I(10 ms) 7.44#10
44
A 9 0
<< !! In the circuit oI Figure 30-20, let E
0
12.0 V, R 3.0 *, and L 0.6 H. The switch is closed at time t 0.
At time t 0.5 s, Iind (a) the rate at which the battery supplies power, (b) the rate oI Joule heating, and (c) the
rate at which energy is being stored in the inductor.
(a) 1. Use Equs. 30-21 and 30-22
2. Find I(0.5 s); P IE
(b) P
J
I
2
R
(c) dU
L
/dt LI dI/dt
I 4(1 e
5t
) A; dI/dt 20e
5t
A/s
I 3.67 A; P 44.1 W
P
J
40.4 W
dI/dt 1.64 A/s; dU
L
/dt 3.62 W P P
J
<= !! Do Problem 66 Ior the times t 1 s and t 100 s.
Proceeding as in the preceding problem one obtains, Ior t 1.0 s, I 3.973 A and dI/dt 0.135 A/s. Then:
(a) P 47.7 W; (b) P
J
47.4 W; (c) dU
L
/dt 0.322 W. For t 100 s, I 4.00 A and dI/dt 8 0. So,
(a) P 48.0 W; (b) P
J
48.0 W; (c) dU
L
/dt 0.
<> !! The current in an RL circuit is zero at time t 0 and increases to halI its Iinal value in 4.0 s. (a) What is the
time constant oI this circuit? (b) II the total resistance is 5 *, what is the selI-inductance?
(a) Here e
t/6
0.5; Iind 6Ior t 4 s
(b) L/R 6(Equ. 3-22)
4/6 ln 2; 6 5.77 s
L R6 28.9 H
<?8 !! How many time constants must elapse beIore the current in an RL circuit that is initially zero reaches (a)
90, (b) 99, and (c) 99.9 oI its Iinal value?
(a), (b), (c) 1 e
t/6
x; t/6 ln|1/(1 x)| (a) x 0.9, t/6 2.30; (b) x 0.99, t/6 4.61;
(c) x 0.999, t/6 6.91
=* !! A coil with inductance 4 mH and resistance 150 * is connected across a battery oI emI 12 V and negligible
internal resistance. (a) What is the initial rate oI increase oI the current? (b) What is the rate oI increase when
the current is halI its Iinal value? (c) What is the Iinal current? (d) How long does it take Ior the current to
reach 99 oI its Iinal value?
Chapter 30 Magnetic Induction
(a) From Equs. 30-21 and 30-22, dI/dt E/L e
Rt/L
(b) When I I
0
/2, e
Rt/L
0.5
(c) I
I
E/R
(d) Find t when e
Rt/L
0.01
For t 0, dI/dt 3.0 kA/s
dI/dt 1.5 kA/s
I
I
80 mA
t (L/R) ln 100 0.123 ms
=7 !! A large electromagnet has an inductance oI 50 H and a resistance oI 8.0 *. It is connected to a dc power
source oI 250 V. Find the time Ior the current to reach (a) 10 A and (b) 30 A.
(a) 1. Write I(t) using Equs. 30-21 and 30-22
2. Solve Ior t when (1 e
0.16t
) 0.32
(b) Solve Ior t when (1 e
0.16t
) 0.96
I(t) 31.25(1 e
0.16t
) A
t |ln (1/0.68)|/0.16 2.41 s
t 20.1 s
=9 !! Given the circuit shown in Figure 30-46, assume that switch S has been closed Ior a long time so that
steady currents exist in the circuit and that the inductor L is made oI superconducting wire so that its resistance
may be considered to be zero. (a) Find the battery current, the current in the 100-* resistor, and the current
through the inductor. (b) Find the initial voltage across the inductor when switch S is opened. (c) Give the
current in the inductor as a Iunction oI time measured Irom the instant oI opening switch S.
(a) The 100-* resistor is shorted by L
(b) V
Li
(100 *)(1 A)
(c) I
L
(t) I
L
(0) e
Rt/L
I 1 A; I
100
0; I
L
1 A
V
Li
100 V
I
L
(t) e
50t
A
=)8 !! Compute the initial slope dI/dt at t 0 Irom Equation 30-24, and show that iI the current decreased steadily
at this rate, it would be zero aIter one time constant.
I I
0
e
t/6
; dI/dt (1/6)I
0
e
t/6
. At t 0, dI/dt I
0
/6. II I is a linear Iunction oI t, then I I
0
(1 t/6) and
I 0 at t 6.
=: !! An inductance L and resistance R are connected in series with a battery as in Figure 30-22. A long time
aIter switch S
1
is closed, the current is 2.5 A. When the battery is switched out oI the circuit by opening switch
S
1
and closing S
2
, the current drops to 1.5 A in 45 ms. (a) What is the time constant Ior this circuit? (b) II R
0.4 *, what is L?
(a) I I
0
e
t/6
; solve Ior 6
(b) L 6R
e
0.045/6
0.6; 6 0.0881 s
L 35.2 mH
=; !! When the current in a certain coil is 5.0 A and is increasing at the rate oI 10.0 A/s, the potential diIIerence
across the coil is 140 V. When the current is 5.0 A and is decreasing at the rate oI 10 A/s, the potential
diIIerence is 60 V. Find the resistance and selI-inductance oI the coil.
1. V IR + L dI/dt; write the two conditions given
2. Solve Ior R and L
140 5R 10L; 60 5R - 10L
R 20 *, L 4 H
=< !! For the circuit oI Figure 30-47, (a) Iind the rate oI change oI the current in each inductor and in the resistor
just aIter the switch is closed. (b) What is the Iinal current? (Use the result Irom Problem 92.)
(a) 1. Find L
eII
and 6; see Problem 30-92
2. At t 0, dI
R
/dt E/L
3. Note that at t 0, IR 0; L dI
L
/dt E
L
eII
2.67 mH
dI
R
/dt 9.0 kA/s
L 8 mH, dI
L
/dt 3 kA/s; L 4 mH, dI
L
/dt 6 kA/s
Chapter 30 Magnetic Induction
(b) I
I
E/R I
I
1.6 A
==8 !! For the circuit oI Example 30-11, Iind the time at which the power dissipation in the resistor equals the rate
at which magnetic energy is stored in the inductor.
1. Find the rate oI energy storage in L
2. Set I
2
R LI(dI/dt)
3. Solve Ior t/6and Iind t Ior 6 333 s
dU
L
/dt d(1/2LI
2
)/dt LI(dI/dt)
1/6 (1/I)(dI/dt) e
t/6
/|6(1 e
t/6
)|
t/6 ln(2); t 231 s
=> !!! In the circuit oI Figure 30-21, let E
0
12.0 V, R 3.0 *, and L 0.6 H. The switch is closed at time t 0.
From time t 0 to t 6, Iind (a) the total energy that has been supplied by the battery, (b) the total energy that
has been dissipated in the resistor, and (c) the energy that has been stored in the inductor. (Hint: Find the rates
as Iunctions oI time and integrate Irom t 0 to t 6 L/R.)
(a) Integrate P EI Irom 0 to 6; 6 L/R and I is
given by Equ. 30-21
(b) Integrate I
2
R Irom 0 to 6with I given by
Equ. 30-21
(c) At t 6, U
L
1/2LI
2
(E
2
L/R
2
)(1 e
1
)
2
(E
2
/R) ( )
.
/
/
T
T t
dt e
0
/
1 E
2
6/Re E
2
L/R
2
e; E 3.53 J
(E
2
/R) ( )
.
/ /
+ /
T
T t T t
dt e e
0
/ 2 /
2 1 (E
2
/R)(26/e 6/2
6/2e
2
);
E
J
0.168E
2
L/R
2
1.61 J
U
L
1.92 J; note that U
L
E
J
E
=? ! Two identical bar magnets are dropped Irom equal heights. Magnet A is dropped Irom above bare earth,
whereas magnet B is dropped Irom above a metal plate. Which magnet strikes Iirst? (a) Magnet A (b) Magnet
B (c) Both strike at the same time. (d) Whichever has the N pole toward the ground. (e) Whichever has the S
pole toward the ground.
(a)
>* ! True or Ialse:
(a) The induced emI in a circuit is proportional to the magnetic Ilux through the circuit.
(b) There can be an induced emI at an instant when the Ilux through the circuit is zero.
(c) Lenz's law is related to the conservation oI energy.
(d) The inductance oI a solenoid is proportional to the rate oI change oI the current in it.
(e) The magnetic energy density at some point in space is proportional to the square oI the
magnetic Iield at that point.
(a) False (b) True (c) True (d) False (e) True
>78 ! A bar magnet is dropped inside a long vertical tube. II the tube is made oI metal, the magnet quickly
approaches a terminal speed, but iI the tube is made oI cardboard, it does not. Explain.
The time varying magnetic Iield oI the magnet sets up eddy currents in the metal tube.The eddy currents
establish a magnetic Iield with a magnetic moment opposite to that oI the moving magnet; thus the magnet is
slowed down. II the tube is made oI a nonconducting material, there are no eddy currents.
>9 ! A circular coil oI radius 3.0 cm has 6 turns. A magnetic Iield B 5000 G is perpendicular to the coil. (a)
Chapter 30 Magnetic Induction
Find the magnetic Ilux through the coil. (b) Find the magnetic Ilux through the coil iI the coil makes an angle
oI 20 with the magnetic Iield.
(a), (b) Use Equ. 30-3; B 0.5 T; A 2.83#10
3
m
2
(a) "m
8.48 mWb; (b) "m
7.97 mWb
>) ! The magnetic Iield in Problem 82 is steadily reduced to zero in 1.2 s. Find the emI induced in the coil when
(a) the magnetic Iield is perpendicular to the coil and (b) the magnetic Iield makes an angle oI 20 with the
normal to the coil.
(a), (b) Use Equ. 30-5; E +"/+t "m
/+t (a) E 7.07 mV; (b) E 6.64 mV
>: ! A 100-turn coil has a radius oI 4.0 cm and a resistance oI 25 *. At what rate must a perpendicular magnetic
Iield change to produce a current oI 4.0 A in the coil?
From Equ. 30-5, E IR NA(dB/dt) dB/dt IR/NA 199 T/s
>;8 !! Figure 30-48 shows an ac generator. It consists oI a rectangular loop oI dimensions a and b with N turns
connected to slip rings. The loop rotates with an angular velocity - in a uniIorm magnetic Iield B. (a) Show
that the potential diIIerence between the two slip rings is E NBab- sin wt. (b) II a 1.0 cm, b 2.0 cm, N
1000, and B 2 T, at what angular Irequency - must the coil rotate to generate an emI whose maximum value
is 110 V?
(a) Find "m
(t) and E d"m
/dt
(b) E
max
Ior sin -t 1; solve Ior -
"m
(t) NBA cos -t; E NBab- sin -t
- 110/(1000#2#10
4
#2) 275 rad/s
>< !! Prior to about 1960, magnetic Iield strength was measured by means oI a rotating coil gaussmeter. This
device used a small loop oI many turns rotating on an axis perpendicular to the magnetic Iield at Iairly high
speed and connected to an ac voltmeter by means oI slip rings like those shown in Figure 30-48. The sensing
coil Ior a rotating coil gaussmeter has 400 turns and an area oI 1.4 cm
2
. The coil rotates at 180 rpm. II the
magnetic Iield strength is 0.45 T, Iind the maximum induced emI in the coil and the orientation oI the coil
relative to the Iield Ior which this maximum induced emI occurs.
Use the result oI Problem 30-85 E
max
(400#0.45#1.4#10
4
#18.85) V 0.475 V when
the plane oI the coil is parallel to the magnetic Iield.
>= !! Show that the eIIective inductance Ior two inductors L
1
and L
2
connected in series such that none oI the
Ilux Irom either passes through the other is given by L
eII
L
1
L
2
.
Since the inductors L
1
and L
2
are in series, I
1
I
2
I and dI
1
/dt dI
2
/dt dI/dt. The total induced emI is E
E
1
E
2
(L
1
L
2
) dI/dt L
eII
dI/dt. So L
eII
L
1
L
2
.
>> !! The rectangular coil in Figure 30-49 has 80 turns, is 25 cm wide and 30 cm long, and is located in a
magnetic Iield B 1.4 T directed out oI the page as shown, with only halI oI the coil in the region oI the
magnetic Iield. The resistance oI the coil is 24 *. Find the magnitude and direction oI the induced current iI the
coil is moved with a speed oI 2 m/s (a) to the right, (b) up, (c) to the leIt, and (d) down.
(a), (b), (c), (d) Proceed as in Example 30-6 (a) and (c): E 0 and I 0; (b) and (d): I 2.33 A;
Ior (b) I is clockwise, Ior (d) I is counterclockwise
>?8!! Suppose the coil oI Problem 88 is rotated about its vertical centerline at constant angular velocity oI 2
Chapter 30 Magnetic Induction
rad/s. Find the induced current as a Iunction oI time.
From Problem 85, I E/R (NBA- sin -t)/R I(t) (80#0.0375#1.4#2/24) sin 2t A 0.35

sin 2t A
?* !! Suppose the coil oI Problem 88 is rotated about its horizontal centerline at constant angular velocity oI 2
rad/s. Find the induced current as a Iunction oI time.
Since the rotation is about the centerline, d"m
/dt is the same as in Problem 30-89. So I 0.35 sin 2t.
?7 !! Show that iI the Ilux through each turn oI an N-turn coil oI resistance R changes Irom "m1
to "m2
, the total
charge passing through the coil is given by Q N("m1
"m2
)/R.
The induced current is I E/R (N/R) d"m
/dt dQ/dt. So dQ (N/R) d"m
, and integrating both sides one
obtains +Q (N/R)(" m1
"m2
).
?9 !! Show that the eIIective inductance Ior two inductors L
1
and L
2
connected in parallel such that none oI the
Ilux Irom either passes through the other is given by
L L L 2 1 eII
1

1

1
For the parallel connection, E
1
E
2
E and I I
1
I
2
and dI/dt dI
1
/dt + dI
2
/dt. The emIs are E L
1
dI
1
/dt
and E L
2
dI
2
/dt. DeIine L
eII
by L
eII
E/(dI/dt). Then L
eII
E/(E/L
1
E/L
2
) L
1
L
2
/(L
1
L
2
) or 1/L
eII
1/L
1

1/L
2
.
?)8 !! A long solenoid has n turns per unit length and carries a current given by I I
0
sin wt. The solenoid has a
circular cross section oI radius R. Find the induced electric Iield at a radius r Irom the axis oI the solenoid Ior
(a) r R and (b) r ~ R.
(a) The Iield within the solenoid is B 0
nI. The Ilux through an area $r
2
Ior r R is then "m
$r
2
0
nI. We
now apply Equ. 30-5 and obtain 2$rE d"m
/dt. Solving Ior E we Iind E (0
nrI
0- /2) cos -t.
(b) Proceed as in part (a) with "m
$R
2
0
nI. One obtains E (0
nR
2
I
0- /2r) cos -t.
?: !!! A thin-walled hollow wire oI radius a lies with its axis along the z axis and carries current I in the positive
z direction. A second identical wire is parallel to the Iirst with its axis along the line x d. The second wire
carries current I in the negative z direction. (a) Find the magnetic Ilux per unit length through the space in the
xz plane between the wires. (b) II the Iar ends oI the wires are connected together so that the parallel wires Iorm
two sides oI a loop, Iind the selI-inductance per unit length oI the loop.
(a) Since the two wires carry the same current but in opposite directions, the Iields produced by them in the
region between the wires are in the same direction. Moreover, the total Ilux in this region is just twice the Ilux
due to the current in one oI the wires. We can now use the result oI Problem 30-10, with b 1 m, d replaced by
a, and a replaced by d 2a. Thus the Ilux per unit length due to the currents in the two wires in the speciIied
region is "m
(o
I/$) ln|(d a)/a|.
(b) From the deIinition oI L, Equ. 30-7, L (0
/$) ln|(d a)/a|
?; !!! A coaxial cable consists oI two very thin-walled conducting cylinders oI radii r
1
and r
2
(Figure 30-50).
Current I goes in one direction down the inner cylinder and in the opposite direction in the outer cylinder. (a)
Use Ampere's law to Iind B. Show that B 0 except in the region between the conductors. (b) Show that the
magnetic energy density in the region between the cylinders is
r
8
I

2 2
2
0
m
$

u
(c) Find the magnetic energy in a cylindrical shell volume element oI length ! and volume dV ! 2$r dr, and
integrate your result to show that the total magnetic energy in the volume oI length ! is
Chapter 30 Magnetic Induction
r
r
I U
1
2 2
ln
4

0
m
!
$

(d) Use the result in part (c) and U

m

2
1
0LI
2
to show that the selI-inductance per unit length is
r
r
=
L
1
2
ln
2
0
$

!
(a) The system exhibits cylindrical symmetry, so one can use Ampere`s law to determine B. For r r
1
and Ior r ~
r
2
the net enclosed current is zero; consequently, in these regions B 0. For r
1
r r
2
, 2$rB 0
I and B
0
I/2$r.
(b) u
m
is given by Equ. 30-17; i.e., u
m
0
I
2
/8$
2
r
2
in the region between the two cylinders.
(c) U
m
.u
m
dV, where dV 2$r ! dr. Integrating Irom r r
1
to r r
2
one obtains U
m
(0
! I
2
/4$) ln(r
2
/r
1
).
(d) Set ! 1 m and use the relation U
m
1/2LI
2
. Then L (0
/2$) ln(r
2
/r
1
) per unit length.
?< !!! In Figure 30-50, compute the Ilux through a rectangular area oI sides ! and r
2
r
1
between the conductors.
Show that the selI-inductance per unit length can be Iound Irom "m
LI (see part (d) oI Problem 95).
Consider a strip oI unit length and width dr at a distance r Irom the axis. The Ilux through this area is given by
d"m
B dA B dr (0
I/2$) dr/r. Integrating Irom r r
1
to r r
2
one obtains "m
(0
I/2$) ln(r
2
/r
1
). Using the
deIinition Ior L, Equ. 30-7, L (0
/2$) ln(r
2
/r
1
).
?=8 !!! Figure 30-51 shows a rectangular loop oI wire, 0.30 m wide and 1.50 m long, in the vertical plane and
perpendicular to a uniIorm magnetic Iield B 0.40 T, directed inward as shown. The portion oI the loop not in
the magnetic Iield is 0.10 m long. The resistance oI the loop is 0.20 * and its mass is 0.50 kg. The loop is
released Irom rest at t 0. (a) What is the magnitude and direction oI the induced current when the loop has a
downward velocity v? (b) What is the Iorce that acts on the loop as a result oI this current? (c) What is the net
Iorce acting on the loop? (d) Write the equation oI motion oI the loop. (e) Obtain an expression Ior the velocity
oI the loop as a Iunction oI time. (f) Integrate the expression obtained in part (e) to Iind the displacement y as a
Iunction oI time. (g) From the result obtained in part (f) Iind t Ior y 1.40 m, i.e., the time when the loop leaves
the region oI magnetic Iield. (h) Find the velocity oI the loop at that instant. (i) What would be the velocity oI
the loop aIter it has dropped 1.40 m iI B 0?
(a) E Bv ! ; I E/R; use Lenz`s law
(b) F
v
BI ! directed up
(c) F
net
mg F
v
(d) F
net
ma m(dv/dt)
(e) See Problem 5-88
(f) y(t) .v(t) dt
(g) Find t Ior y 1.40 m by trial and error
(h) Find v(0.538 s) Irom part (e)
(i) h g 2 = v
I (0.4#0.3/0.2)v A 0.6v A, clockwise
F
v
(0.4#0.3#0.6)v A 0.072v N, directed up
F
net
(0.5g 0.072v) N, directed down
0.5g 0.072v 0.5(dv/dt)
v(t) 68.1(1 e
0.144t
) m/s
y(t) 68.1|t 6.94(e
0.144t
1)| m
t 0.538 s
v(0.538 s) 5.08 m/s
v 5.24 m/s
?> !!! The loop oI Problem 97 is attached to a plastic spring oI spring constant : (Figure 30-52). (a) When B 0,
the period oI small-amplitude vertical oscillations oI the massspring system is 0.8 s. Find the spring constant
:. (b) When B ; 0, a current is induced in the loop as a result oI its up and down motion. Obtain an expression
Ior the induced current as a Iunction oI time when B 0.40 T. (c) Show that the induced current acts as a
damping mechanism. (d) Determine the value oI the magnetic Iield Ior which the Q oI the massspring system
is 100.
Chapter 30 Magnetic Induction
(a) Use Equ. 14-12; : 4$
2
m/T
2
(b) Let y y
0
sin -t; Iind E/R; E Bv !
(c) The damping Iorce is oI the Iorm F
d
bv
(d) 1. Find the energy loss per cycle
2. Write the energy oI the oscillator
3. Q 2$E/+E; solve Ior B
: 30.8 N/m
E@R |(0.4#0.3#7.85y
0
/0.2) cos 7.85t| A
I (4.71y
0
sin 7.85t) A
F
d
BI ! (0.565y
0
cos 7.85t) N
. .
= = = +
T T
y B tdt y B Rdt I E
0 0
2
0
2 2 2
0
2 2
87 . 13 cos 73 . 27 -
E 1/2
:y
0
2
15.4y
0
2
B
2
(15.4#2$/1387) T
2
; B 0.264 T
??8!!! Show that the eIIective inductance oI two inductors, L
1
and L
2
, connected in series and in close proximity, is
L
eII
L
1
L
2
+ 2M. When should the plus sign be used in this expression, and when should the minus sign be
used?
We need to Iind L in terms oI L
1
, L
2
, and M. We recall that the Ilux in the coil L
1
is "m1
+ I
2
M and the Ilux in the
coil L
2
is "m2
+ I
1
M, where we have used "mi
to denote the Ilux due to each inductor when isolated Irom the
other. Since the same current Ilows through both inductors, the total Ilux linking the two inductors is
"m
L
1
I + L
2
I + 2MI, and consequently L
eII
L
1
L
2
+ 2M. The positive sign should be used iI the two
inductors are wound in the same sense so that the Iluxes add, the negative sign iI the inductors are wound in an
opposing sense so that the Iluxes subtract.