Lewandowski 1

Sarah Lewandowski
Mr. Acre
AP Calculus
10 February 2014
Solids of Revolution
One of the major topics in calculus is solids of revolution, revolving an area on a graph
360 degrees in order to create a solid. This topic incorporates many ideas, such as area under a
curve, area between two curves, and many different methods of finding volume of the solid.
These topics will be explained and explored in detail, along with sample problems and the
method of solving them.
Finding the area under a curve is one of the most basic ideas involved in finding the
volume of solids. A definite integral is the area bounded by the function and the x-axis between
the two limits. The notation for a definite integral is
()

where a is the lower limit, b is the upper limit, f(x) is the function in question, and dx is the
change in x. An integral is found by creating infinitely many rectangles, all with a height of f(x),
or the distance from the x-axis, and a width of dx,
where dx is infinitely small. Area of a rectangle is
found by multiplying length and width; when
calculating an integral, the length
and width are f(x) and dx. The area of each of
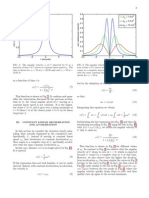
these rectangles is found and then integrated, Figure 1. Area Under a Curve
b a
Lewandowski 2

or summed up, in order to find the total area from a to b. Figure 1 on the previous page shows a
sample function f(x) where a is the lower limit, b is the upper limit, and dx is the width of one of
the infinitely many intervals. Note that dx would not actually appear this big, because it is
infinitely small. When computing the definite integral from a to b, a is the lower limit and b is
the upper limit, meaning that the area between a and b is what is desired, or, in other words,
integration begins at a and ends at b. The green space on the graph shows a sample rectangle. It
would appear that the top of this rectangle is curved because f(x) is curved, but when dx becomes
infinitely small it will become a rectangle, or close enough to a rectangle that finding the area of
all of these will give the true area. The width of this interval is dx and the height is f(x), so the
product or dx and f(x) is the area of the interval. When this area is integrated from a to b, the
total area under the curve is found.
To find the area between two curves, a very similar process is used. The notation is still
the same because a definite integral is still being used. The a and b values, or the limits, are
nearly the same. To find the limits, it is necessary to find where the two graphs intersect and
create an area between them. The x-value of the first intersection point will be the lower limit, or
the a value, and the x-value of the second intersection point will be the upper limit, or the b
value. Also, f(x) changes slightly. When finding the area under the curve, f(x) was the distance
between the curve and the x-axis, or the height of each of the infinite rectangles. Now, f(x) is still
the height of each of the rectangles, but it is the distance between the curves. In Figure 2 below,
the distance between the two graphs is the blue function minus the red function, or -

. What
remains the same is dx it is still the change in x or the width of each of the rectangles. A
sample rectangle is shown in green in Figure 2; the area of all of these rectangles is added up to
Lewandowski 3

find the total area between the two curves. A definite integral used when finding the area
between two curves would therefore look like (() ()

.
For all sample problems done in this paper, let R be the region in the first quadrant
bounded by the graphs of and

, as shown in Figure 2. To find the area of R, or the

area between and

, a definite integral must be used. Set up an integral in the form

of ()

, where a (the lower

limit) is the x-value of the first
intersection of the graphs and b (the
upper limit) is the x-value of the
second intersection of the graphs.
The intersections of these graphs,
which can be found through
Figure 2. Sample Problem Graphs graphing technology and other
techniques, occur at the points (0,0) and (9,3). The lower limit of the integral would then be 0
and the upper limit would be 9. The height of each rectangle is also needed. Since the area
between the curves is being found, the distance between the curves (and also the height of each
rectangle) is the top function minus the bottom function; in this case, f(x) = -

. The integral
should now look like (

. When this integral is evaluated, it shows that the area

between the two curves is 4.5 square units.
A method used to find the volume of a solid with no hole in the middle is the disk
method. This is commonly used when revolving an area bounded by a function and the x-axis
around the x-axis. A graph such as the one shown in Figure 3 can be used in a problem like this.
a
b
Lewandowski 4

If the area under the curve is found or drawn, it can be revolved around the x-axis to make a
solid like the one in Figure 4. Figure 4 shows a completely solid object.

Figure 3. Graph used for Revolution Figure 4. Solid Created by Revolution
To find the volume of an object like the one in Figure 4, the disk method can be used. The disk
method involves creating an infinite number of solid disks, and then finding the volume of each
one and integrating to find the total volume. A circular disk can be sliced out of the object in
Figure 4 perpendicular to the x-axis. This is similar to creating a dx cut when finding the area
under a curve. The disk is a cross-section of the object. Finding the volume of one of these
infinitely many disks will allow one to add them all up by integrating and find the volume of the
entire solid. These disks can also be considered cylinders. To find the volume of one
cylinder/disk, the formula is

. The radius of the cylinder, since the cylinder is

inscribed in the solid, is f(x), or y, from the function in Figure 3. The height of the cylinder is dx,
because it is a dx cut that is created in the object when a slice is taken out. The axis of rotation,
the x-axis, is perpendicular to the dx cut that is made. The integral for this method looks like

, where y is the function in Figure 3, revolved around the x-axis in Figure 4. The can
be pulled out in front of the integral so that the answer can be in terms of . This integral will
produce the total volume of the solid.
a b
Lewandowski 5

The ring method is used when finding the volume of a hollow solid, or a solid with a hole
in the middle. The area between two curves is revolved around an axis of rotation and forms a
solid with thicker walls but a hole in the middle. Let R be the region in the first quadrant
bounded by the graphs of and

, as shown in Figure 5. When the

region R is rotated about the horizontal line
y = -2, a solid will be created with a hole
through the middle, parallel to the x-axis,
and with walls bound by the graphs of
Figure 5. Sample Problem Graphs and

, very similar to Figure 4

but with a hole through the middle. The ring method is similar to the disk method in that
cylinders are used to find the volume of the solid, and the same dx cut is used, perpendicular to
the axis of rotation. It is different in that since there is a hole in the middle, the inner cylinders
volume must be subtracted from the outer cylinders volume. The formula that would be used is

. This can be simplified down to (

). The height is the same

it remains dx so only the radii remain. Do not forget that the area between the curves is being
revolved around y = -2, not y = 0. The radius of the outer cylinder is (2+y) or (2+ ) because
it is f(x) plus the two units it is away from the axis of rotation. The radius of the inner cylinder
will also be (2+y) or (2+

) because it is also f(x) plus the two units it is away from the axis of
rotation. The setup definite integral of this problem looks like (( )

.
When the integral is calculated, the volume of the solid comes out to be 98.96 units cubed.
a
b
Lewandowski 6

Another method that can be used to determine the volume of a solid is the shell method.
The shell method is most useful when the axis of rotation is, or is parallel to, x = 0. A dy cut can
be used in both the disk and ring method,
but it can be much more difficult to use,
and that is why the shell method is used,
because a dx cut is used in the shell
method. Figure 6 will be used to explain
the shell method. In this example, the area
bound by the red and blue graphs is being Figure 6. Example Shell Method
revolved around the y-axis. The ring method could be used; however, the equation would have to
be manipulated so that it is in terms of y instead of x, and this can be nearly impossible to do.
The shell method is done by creating infinitely many cylinders and finding the surface area of
each one in order to find the total volume of the revolved solid. A cylinder is created with a
height of the vertical distance between the curves. The center of the cylinder is the y-axis, and
the radius of the cylinder is x, as shown in Figure 7. The
green part in the diagram is the revolved solid, but it has
only been revolved halfway around so that it can be
seen. The surface area of each one of these cylinders is
found so that when they are all added up, they will equal
the volume of the solid. There are infinitely many
Figure 7. Shell Method cylinders because dx is the thickness of the cylinder and
dx is infinitely small. The surface area formula that is to be used is . The radius of the
cylinder is x and the height of the cylinder is the top function minus the bottom function, so the
a
b
Lewandowski 7

integral of this would look like (

, where the area being revolved is bound by

y1 and y2, and a and b are the lower and upper limits, respectively. This will give the volume of
this solid, which has been revolved around the y-axis.
One final method that can be used to determine the volume of a solid is the cross-section
method. Let R be the region in the first quadrant
bounded by the graphs of and

,
as shown in Figure 8. The base of the solid is
the region R. The cross-sectional method
involves placing the base of a shape, such as a
triangle, circle, or square, between the top
function and the bottom function so that it Figure 8. Cross-Section Example
touches both, perpendicular to the x-axis. The area of each one of these shapes is found, and then
integrated, using a dx cut. This totaled area will give the volume of the solid whose base sits in
the region R. Figure 9 shows an example of one of these
shapes and the solid it fills. A dx cut is being used
because the cross-sections are perpendicular to the x-axis.
In a particular example, the region R is the base of a solid.
The cross-sections perpendicular to the x-axis are
isoscoles right triangles with one leg on the base. The
Figure 9. Cross-Sections volume of the solid can be found by first finding the area
of each triangle. The area of a triangle is

. In this case, the triangles are isoscoles right

triangles, therefore the base and height are equal. The base of the triangle is the distance between
the two functions, so

. The integral for this problem would be

a
b
Lewandowski 8

, giving a final volume of the solid of 1.35 cubic units.

There are a variety of methods available to find the volume of a solid or a revolved solid.
These methods are the disk method, ring method, shell method, and cross-section method. The
area under curves and between curves is also an important focus when finding volume of solids.
It is beneficial to know all of these methods instead of just one because some are extremely easy
to use in certain situations while some are extremely difficult. Knowing all of the methods well
could be the difference between a 4 and a 5 on the AP Calculus exam, and either getting credit or
not getting credit for a college class.













*Figures1, 2, 3, 5, 6, and 8 were made using graphsketch.com
*Figure 4 was made using Microsoft Paint
*Figure 7 - http://www.mathdemos.org/mathdemos/shellmethod/2curve1shell.gif
*Figure 9 - http://library.thinkquest.org/3616/Calc/S3/cross.jpg