RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 1 of 11

Raffles Institution
2011 Year 6 Preliminary Examination Paper 2
H2 Mathematics 9740

SOLUTIONS

Section A: Pure Mathematics [40 marks]

1

[6m]
Since one of the root of the equation is 1 2i +
( ) ( ) ( )
4 3
1 2i 1 2i 10 1 2i 25 0 a + + + + =

( ) ( ) ( ) 7 24i 11 2i 10 20i 25 0 a + + =
11 2 i= 22 4i a a

( 11 2 ) 2( 11 2 ) a i i =


OR: Compare real or imaginary part:

11 22 or 2 4 a a = =

a = 2 (since a is real)


Clearly, the other root is 1 2i
4 3
2 10 25 0 z z z + =
2
( 1 2i)( 1 2i)( ) z z z bz c = + + +
2 2
( 2 5)( 5) z z z bz = + + (by inspection, 5 c = )
2 5 5 0 b + = (compare coefficient of
2
z )
0 b =

4 3
2 10 25 z z z +
2 2
( 2 5)( 5) z z z = + 0 =

1 2i, 1 2i, 5, 5 z = +

Let z = (w 1 )
Therefore w = 2i, 2i, 1 5, 1 5 +

2(i)
[1m]
Since
42 43 44
, , a a a are in AP,
44 43 43 42
44 43 42
3 2 4
2 2 .
81 81 81
a a a a
a a a
=
| |
= = =
|
\ .


(ii)
[2m]
Since
24 34 44
, , a a a are in GP,
2 2 2
44 24
4 4 1
81 9 9
a a r r r = = =
1
3
r =
Since the array contains positive real numbers, r > 0 so
1
3
r = .

2(iii) We have
RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 2 of 11
[3m]
24 14 11
3 3
42 12 11
( 3 ) ...(1)
( ) ...(2)
a a r a d r
a a r a d r
= = +
= = +

Hence
24 11 11
42 11 11
4 1 4
( 3 ) 3
9 3 3
2 1 2
( )
81 27 3
a a d a d
a a d a d
= = + = +
= = + = +

Solving both equations (via GC) or simply subtracting the 2
nd
equation from the 1
st
, we
get a
11
= d =
1
3
.

Alternatively,
3
42 41 11
1 1
81 81
a a a r = + = + . Solve simultaneously with (1).

(iv)

[2m]
Method 1
1
1
1
11
1
1
( ( 1) )
1 1 1
( 1)
3 3 3
1 1
(1 ( 1))
3 3
1
3
k
kk k
k
k
k
k
a a r
a k d r
k
k
k

=
= +
| || |
= +
| |
\ .\ .
| |
= +
|
\ .
| |
=
|
\ .

Method 2
1
1
1 1
11
1 1
( 1)
( 1)
1 1 1 1
( 1)
3 3 3 3
1
(1 1)
3
1
3
k
kk k
k k
k k
k
k
a a k dr
a r k dr
k
k
k

= +
= +
| | | |
= +
| |
\ . \ .
| |
= +
|
\ .
| |
=
|
\ .


(v)

[3m]
( )
( )
2 3
2 2 1
2 3 1
1 1
3 3
1
1
3
1
3 1
1 1 2 3
3 3 3 3 3
1 2 1
3 3 3 3
1 1 1 1
3 3 3 3 3
(1 )
1 3
1
(1 ) .
2 3
n n n
n n
n n
n
n
n
n
n
S S
n n
n
n
n
+
+
+
+
= + + + +

= + + + +

Hence
( )
1
3 1
2 1 3 1
(1 ) 1 .
3 2 3 4 3 2(3 )
n
n n n n n
n n
S S
+
| |
= =
|
\ .





RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 3 of 11
3(i)
[1m]

3(ii)
[3m]
At
4 4
sin , cos ) ( , b a u u

3 3
d
sin cos and 4 cos sin ,
d
d
4
d
y
b
x
a u u u u
u u
= =
so
3 2
2 3
2
cos sin cos
cot (Shown).
sin co
d 4 d d
d d d 4 s sin
y b b b y x
x a a a
u u u
u
u u u u u

= = = =
3(iii)
[3m]
The equation of the tangent at
4 4
sin , cos ( ) b a u u is

( )
4 2 4
cos co s . t in
b
y b x a
a
u u u =
Setting 0 y = and solving for x gives

( )
2 2 2 2
sin cos sin sin . x a a u u u u + = =

Coordinates of P are
2
( sin , 0). a u
Similarly, setting 0 x = and solving for y gives
2
cos . y b u =

Coordinates of Q are (0,
2
cos ) b u .
3(iv)
[3m]
From (iii),
2
sin OP a u = and
2
cos , OQ b u = so

2 2 2
sin co
1
( )( )
2
s sin 2
8 2
.
ab
A OP O
ab
Q u u u = = =
A is maximum when sin 2u = 1, i.e.
4
t
u = for 0, ,
2
t
u
| |
e
|
\ .

Maximum value of
2
sin 2 .
8 4 8
ab b
A
a t | |
= =
|
\ .


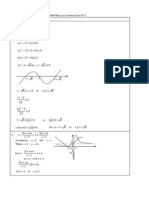
x
O
y
2
1
4
4
, sin
cos y
a
b
x u
u =
=
RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 4 of 11
Alternatively,
From (iii),
2
sin OP a u = and
2
cos , OQ b u = so

2 2
1
( )( ) sin cos .
2 2
ab
A OP OQ u u = =

( ) ( )
3 3 2 2
2 2 2
sin cos 2sin cos cos sin
For 0, ,
2
when
d
2 sin cos
d 2
d
0, cos sin t
d
an 1
4
A ab
ab
A
u u u u u u
t
u
t
u u u u
u u
u
u
=
| |
e
|
\ .
= = =
=
=

Maximum value of
4
2 2
1
sin cos .
2 4 4 2 8 2
ab ab ab
A
t t | | | | | |
= = =
| | |
\ . \ . \ .

4(i)

[3m]
For
1
l and
2
l to intersect,
2 0 1
0 1 = 3 0 for some , .
1 5 4 2
p

| | | | | | | |
| | | |
+ + e
| | | |
\ . \ . \ . \ .


2 0
3 3, 6, 0
5 2 3
p
p



+ =

= = = =
`

=
)

Hence coordinates of (6, 3,16) A =


4(ii)

[3m]
3
l has equation
2
0 1 ,
1 5
q
o o
| | | |
| |
= + e
| |
\ . \ .
r

3
2 2 2
2 2
2
0 1
1 5
Shortest distance from to
2
1
5
2 6
1
3 1
2 ( 1) 5
15 5
0
1
5
30
5 1 (since 0)
30
13
15
q
OA
A l
q
q
q
q
q
q
| | | | | |
| | |

| | |
\ . \ . \ .
=
| |
|

|
\ .
| | | |
| |
=
| |
+ +
\ . \ .
| |
|
=
|
\ .
= + >
=

RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 5 of 11

4(iii)

[4m]
2
0 1 for some
1 5
q
OB
| | | |
| |
= + e
| |
| |
\ . \ .

o o

15 13
Now , so 15 by (i).
15
AB q = =

1
2 2 2
2
Since , 1 0
5
9 2 2
3 1 1 0
15 5 5
(18 3 75) (2 ( 1) 5 ) 0
60
2
30
15 2 19
So 0 2 1 2
1 5 11
AB l AB
OB
o
o
o
| |
|
=
|
\ .
| | | | | | | |
| | | |
+ =
| | | |

\ . \ . \ . \ .
+ + + =
= =
| | | | | |
| | |
= + =
| | |
\ . \ . \ .

4(iv)

[3m]
Note that (0, 0,1) and (15,0,1)

lie on
1
l and
3
l respectively, so they lie on
1
H , and hence
a vector parallel to
1
H is
15 0 15 1
0 0 0 15 0
1 1 0 0
| | | | | | | |
| | | |
= =
| | | |
\ . \ . \ . \ .
.
So a normal vector to
1
H is
1 2 0 0
0 1 5 ( 1) 5
0 5 1 1
| | | | | | | |
| | | |
= =
| | | |

\ . \ . \ . \ .
.
So equation of
1
H is
0 0 0
5 0 5
1 1 1
| | | | | |
| | |
=
| | |
\ . \ . \ .
r
0
5 1
1
r
| |
|
=
|
\ .





Section B: Statistics [60 marks]

5(i)
[2m]
Number of ways
15 15 15
0 1
2 C C =
32768 1 15 32752 = =

OR
15
15 15 15 15 15
2 3 4 15
2
32752
r
r
C C C C C
=
= = + + + + =

RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 6 of 11
5(iia)
[1m]
Number of ways 9! 362880 = =

OR

( )
3
9 6 3
3 3 3
3! 362880 C C C = =

5(iib)
[2m]
Number of ways
6
1
2! 7 6048 ! 0 C = =

OR

( )
2
6 7 6 3
1 1 3 3
2! 6 3! 0480 C C C C = =
5(iii)
[2m]

Number of ways = (6 1)! 6 5 4 = 14400
OR

Number of ways ( ) ( ) ( )
3 6
2 2
9 1 ! 7 1 ! 3! 6 1 4 ! 14 00 P P = =
6(i)

[2m]
Probability
2 4 3 5 23
5 10 5 10 50
| || | | || |
= + =
| | | |
\ .\ . \ .\ .


6(ii)

[5m]
Probability
=

P(transferring from A to B and drawing a white ball from B) +
P(transferring from B to A and drawing a white ball from A)
1 23 3 5 3 4 4
4 50 4 9 6 9 6
491
900
( ( | || | | || |
= + +
| | | | ( (
\ .\ . \ .\ .
=



P (ball transferred from A to B final ball chosen is white)
( )
( )
transfer from to andfinal ball chosenis white
final ball chosenis white
P A B
P
=
1 23 23
207 4 50 200
491 491 982
900 900
| || | | |
| | |
\ .\ . \ .
= = =
| |
|
\ .



7(i)

[1m]




7(ii)
[1m]
Product moment correlation coefficient = 0.920 (3 s.f.)
t (hours)
x (micrograms per litre)
RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 7 of 11
7(iii)

[2m]

Equation of the regression line of x on t is
x = 120.743 12.6179t
i.e. x = 121 12.6t (to 3 s.f.)

The gradient 12.6 means that the estimated decrease in the concentration of drug in
the bloodstream is 12.6 micrograms per litre for every 1 hour increase in time.

7(iv)

[2m]
Using the equation of the line in (iii),
when x = 50, t = 5.61,
Estimated time is 5.61 hours.

The estimate is not reliable as the scatter diagram in (i) shows that a curve is a better fit
for the data points, so a linear model is not suitable.

8(i)
[1m]
The probability of concluding that the population mean GPA score is more than 2.9,
when it is actually 2.9, is 0.1.

8(ii)

[6m]
Note: The t-test should be used, because the sample size is small, and the population
variance is unknown.

To test H
0
: = 2.9 vs H
1
: > 2.9

Perform a 1 tail t-test at 10% level of significance.

Under H
0
,
0
~ ( 1)
/
X
T t n
S n

=
where
0
= 2.9, x = 3.12, s = 0.72821, n = 15

Using a t-test, p-value = 0.131 (3 s.f.)

Since p-value = 0.131 > 0.1, we do not reject H
0
and conclude that there is insufficient
evidence at the 10% level of significance that the population mean GPA score is more
than 2.9.

Assumption is that the GPA scores of the student population follow a normal
distribution.


9(i)
[2m]

Let X be the number of students, out of 16, who wore brown shoes to school.
~ (16, 0.17). X B

( 3) 0.244. (3 s.f.) P X = =


9(ii)
[5m]

Let Y be the number of students, out of 60, who wore white shoes to school.
( ) ~ 60, 0.58 . Y B
Since n = 60 > 50 is sufficiently large and p = 0.58 are such that
34.8 5 np = > and (1 ) 25.2 5, n p = >
Therefore ( ) ~ , (1 ) Y N np np p approximately
i.e. ( ) ~ 34.8, 14.616 Y N approximately.
RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 8 of 11
( ) ( ) ( )
( )
38 38.5 by continuity correction
0.167. 3 s.f.
P Y P Y > = >
=



10(i)
[2m]
Let X be the number of defects in a box.

2.5
~ Po 3.2
40
X
| |

|
\ .

i.e. ~ Po(0.2) X

( ) 1 0.98248 0.982 P X s ~ ~ (3 s.f.)

10(ii)
[2m] ( )
(a package is accepted)
box has at most one defect and its barcode is not defective
0.98248 0.96 0.94318 0.943 (3 s.f.)
P
P =
~ = =

10(iii)
[4m]
Let Y be the number of packages, out of 70, that are rejected.

( ) ~ 70,1 0.94318 Y B

Since n = 70 is large, p = 0.05682 is small such that 3.9774 5 np = < , therefore
( ) ~ 3.9774 Y Po approximately.

( )
(more than 67 packages are accepted)
2 0.241 (3 s.f.)
P
P Y = s =


11(i)

[2m]
Let X be mass of an abalone in grams.

( )
2
~ 180, X N o


( ) 200 0.08 P X > =

200 180
0.08 P Z
o
| |
> =
|
\ .

20
0.92 P Z
o
| |
s =
|
\ .

From G.C.,
20
1.4051
14.234 14.2 (3 s.f.) (shown)
o
o
~
~ =

11(ii)
[1m]

( ) 165 0.14541 0.145 (3 s.f.) P X < ~ ~

11(iii)

[3m]


2
14.2
~ 180,
15
X N
| |
|
\ .


RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 9 of 11
( ) ( )
( )
( )
180 5 180 5 ( 180 5)
2 180 5 or 2 ( 180 5)
2 185 or 2 ( 175)
0.173 (3 s.f.)
P X P X P X
P X P X
P X P X
> = > + <
(
= > <

(
= > <

=

Alternative 1,
2
14.2
180 ~ 0,
15
X N
| |

|
\ .


( ) ( )
( )
180 5 180 5 ( 180 5)
2 180 5
0.173 (3 s.f.)
P X P X P X
P X
> = > + <
= >
=

Alternative 2,
( ) ~ 2700, 3024.6 X N

( )
( )
( )
180 5 2700 75
( 2700 75) ( 2700 75)
2 2775
0.173 (3 s.f.)
P X P X
P X P X
P X
> = >
= > + <
= >
=

11(iv)

[3m]
Let C be cost of one abalone in dollars.

( )
( )
2 450
~ 81, 6.39
1000
C X N =


( )
( )
2
1 2 3 4 5
~ 5 81, 5 6.39 T C C C C C N = + + + +

( ) ~ 405, 204.1605 T N

( ) 420 0.147 (3 s.f.) P T > =


Alternatively,

Let ( )
( )
2
1 2 3 4 5
~ 5 180, 5 14.2 W X X X X X N = + + + +

( ) ~ 900, 1008.2 W N

Probability required
( )
450
420
1000
933.33
0.147 (3 s.f.)
P W
P W
| |
= >
|
\ .
= >
=




12(i)
Unbiased estimate of population mean
RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 10 of 11

[2m]












12(ii)

[4m]


































=
( 50)
100
50 50
120
1
49 or 49.167 (5 s.f ) 49.2 (3 s.f )
6
x
n

+ = +
= =

Unbiased estimate of population variance
( )
2
2
2
( 50)
1
( 50)
1
1 ( 100)
(1158 ) 9.0308 9.03 (3 s.f )
119 120
x
x
n n
(

(
=
(

= ~ =

Since n = 120 is large, by Central Limit Theorem,

9.0308
(49.167, ) approximately. X N
n

( 49.9) 0.01
( 49.9) 0.99
49.9 49.167
( ) 0.99
9.0308
49.9 49.167
From , 2.3263
9.0308
90.960
Least value of 91
Method 1: Using Standardization
P X
P X
P Z
n
GC
n
n
n
> s
< >

< >

>
>
=



Method 2 : Using table of values
Key in Y
1
= normalcdf(49.9, E99, 49.167, 9.0308 / X )

n
( 49.9) P X >
90 0.01033 > 0.01
91 0.00999 < 0.01
92 0.00965 < 0.01

Least value of n = 91


The population is first divided into 4 strata according to 4 levels Sec 1 to 4. Random
samples, of sample sizes proportional to the relative sizes of the strata, are then drawn
separately and independently (by using simple random sampling) from each stratum
(level).
OR (divide into 2 strata according to gender)

RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 Page 11 of 11


(iii)









Stratified sampling is a better sampling method compared to simple random sampling
because it is likely to give good representative samples of the population, i.e. students
from each stratum (level or gender) are well represented as in the population.