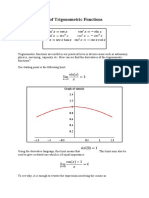
Hyperbolic function

From Wikipedia, the free encyclopedia

Jump to: navigation, search


A ray through the origin intercepts the hyperbola in the point , where
is twice the area between the ray and the -axis. For points on the hyperbola below the -axis,
the area is considered negative (see animated version with comparison with the trigonometric
(circular) functions).
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular,
functions. The basic hyperbolic functions are the hyperbolic sine "sinh" ( /snt/ or /an/),
and the hyperbolic cosine "cosh" ( /k/), from which are derived the hyperbolic tangent
"tanh" ( /tnt/ or /n/
[citation needed]
), and so on, corresponding to the derived trigonometric
functions. The inverse hyperbolic functions are the area hyperbolic sine "arsinh" (also called
"asinh" or sometimes "arcsinh")
[1]
and so on.
Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the
right half of the equilateral hyperbola. Hyperbolic functions occur in the solutions of some
important linear differential equations, for example the equation defining a catenary, and
Laplace's equation in Cartesian coordinates. The latter is important in many areas of physics,
including electromagnetic theory, heat transfer, fluid dynamics, and special relativity.
The hyperbolic functions take real values for a real argument called a hyperbolic angle. In
complex analysis, they are simply rational functions of exponentials, and so are meromorphic.
Hyperbolic functions were introduced in the 1760s independently by Vincenzo Riccati and
Johann Heinrich Lambert.
[2]
Riccati used Sc. and Cc. ([co]sinus circulare) to refer to circular
functions and Sh. and Ch. ([co]sinus hyperbolico) to refer to hyperbolic functions. Lambert
adopted the names but altered the abbreviations to what they are today.
[3]
The abbreviations sh
and ch are still used in some other languages, like French and Russian.
Contents
[show]

[edit] Standard algebraic expressions


sinh, cosh and tanh


csch, sech and coth

(a) cosh(x) is the average of e
x
and e
x


(b) sinh(x) is half the difference of e
x
and e
x

Hyperbolic functions (a) cosh and (b) sinh obtained using exponential functions e
x
and e
x

The hyperbolic functions are:
Hyperbolic sine:

Hyperbolic cosine:

Hyperbolic tangent:

Hyperbolic cotangent:

Hyperbolic secant:

Hyperbolic cosecant:

Hyperbolic functions can be introduced via imaginary circular angles:
Hyperbolic sine:

Hyperbolic cosine:

Hyperbolic tangent:

Hyperbolic cotangent:

Hyperbolic secant:

Hyperbolic cosecant:

where i is the imaginary unit defined as i
2
= 1.
The complex forms in the definitions above derive from Euler's formula.
Note that, by convention, sinh
2
x means (sinh x)
2
, not sinh(sinh x); similarly for the other
hyperbolic functions when used with positive exponents. Another notation for the hyperbolic
cotangent function is ctnh x, though coth x is far more common.
[edit] Useful relations


Hence:




It can be seen that cosh x and sech x are even functions; the others are odd functions.



Hyperbolic sine and cosine satisfy the identity

which is similar to the Pythagorean trigonometric identity. One also has


for the other functions.
The hyperbolic tangent is the solution to the nonlinear boundary value problem
[4]
:

It can be shown that the area under the curve of cosh x is always equal to the arc length:
[5]



[edit] Inverse functions as logarithms






[edit] Derivatives












[edit] Standard Integrals
For a full list of integrals of hyperbolic functions, see list of integrals of hyperbolic functions










Where C is the constant of integration.
[edit] Taylor series expressions
It is possible to express the above functions as Taylor series:

The function sinh x has a Taylor series expression with only odd exponents for x. Thus it is an
odd function, that is, sinh x = sinh(x), and sinh 0 = 0.

The function cosh x has a Taylor series expression with only even exponents for x. Thus it is an
even function, that is, symmetric with respect to the y-axis. The sum of the sinh and cosh series
is the infinite series expression of the exponential function.

(Laurent series)

(Laurent series)
where
is the nth Bernoulli number
is the nth Euler number
[edit] Comparison with circular trigonometric functions
Consider these two subsets of the Cartesian plane

Then A forms the right branch of the unit hyperbola {(x,y): x
2
y
2
= 1}, while B is the unit circle.
Evidently = {(1,0)}. The primary difference is that the map t B is a periodic function
while t A is not.
There is a close analogy of A with B through split-complex numbers in comparison with ordinary
complex numbers, and its circle group.
[clarification needed]
In particular, the maps t A and t B
are the exponential map in each case. They are both instances of one-parameter groups in Lie
theory where all groups evolve out of the identity For contrast, in the
terminology of topological groups, B forms a compact group while A is non-compact since it is
unbounded.
The hyperbolic functions satisfy many identities, all of them similar in form to the trigonometric
identities. In fact, Osborn's rule
[6]
states that one can convert any trigonometric identity into a
hyperbolic identity by expanding it completely in terms of integral powers of sines and cosines,
changing sine to sinh and cosine to cosh, and switching the sign of every term which contains a
product of 2, 6, 10, 14, ... sinhs. This yields for example the addition theorems



the "double argument formulas"



and the "half-argument formulas"
[7]

Note: This is equivalent to its circular counterpart
multiplied by 1.
Note: This corresponds to its circular counterpart.
The derivative of sinh x is cosh x and the derivative of cosh x is sinh x; this is similar to
trigonometric functions, albeit the sign is different (i.e., the derivative of cos x is sin x).
The Gudermannian function gives a direct relationship between the circular functions and the
hyperbolic ones that does not involve complex numbers.
The graph of the function a cosh(x/a) is the catenary, the curve formed by a uniform flexible
chain hanging freely between two fixed points under uniform gravity.
[edit] Relationship to the exponential function
From the definitions of the hyperbolic sine and cosine, we can derive the following identities:

and

These expressions are analogous to the expressions for sine and cosine, based on Euler's formula,
as sums of complex exponentials.
[edit] Hyperbolic functions for complex numbers
Since the exponential function can be defined for any complex argument, we can extend the
definitions of the hyperbolic functions also to complex arguments. The functions sinh z and
cosh z are then holomorphic.
Relationships to ordinary trigonometric functions are given by Euler's formula for complex
numbers:


so:








Thus, hyperbolic functions are periodic with respect to the imaginary component,with period 2i
(i for hyperbolic tangent and cotangent).
Hyperbolic functions in the complex plane