Beruflich Dokumente
Kultur Dokumente
Shallow Foundations Allowable Bearing Capacity & Settlement
Hochgeladen von
MansoorCopyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Shallow Foundations Allowable Bearing Capacity & Settlement
Hochgeladen von
MansoorCopyright:
Verfügbare Formate
NPTEL ADVANCED FOUNDATION ENGINEERING-I
Module 4
Lecture 14
SHALLOW FOUNDATIONS: ALLOWABLE BEARING CAPACITY AND
SETTLEMENT
Topics
1.1 SETTLEMENT CALCULATION
1.2 ELASTIC SETTLEMENT BASED ON THE THEORY OF
ELASTICITY
1.3 ELASTIC SETTLEMENT OF FOUNDATION ON
SATURATED CLAY
1.4 SETTLEMENT OF SANDY SOIL: USE OF STRAIN
INFLUENCE FACTOR
1.5 RANGE OF MATERIAL PARAMETERS FOR COMPUTING
ELASTIC SETTLEMENT
1.6 CONSOLIDATION SETTLEMENT
1.7 SKEMPTON-BJERRUM MODIFICATION FOR CONSOLIDATION
SETTLEMENT
1.8 CONSOLIDATION SETTLEMENT-GENERAL COMMENTS
AND A CASE HISTORY
NPTEL ADVANCED FOUNDATION ENGINEERING-I
SETTLEMENT CALCULATION
ELASTIC SETTLEMENT BASED ON THE THEORY OF ELASTICITY
The elastic settlement of a shallow foundation can be estimated by using the theory of
elasticity. Referring to figure 4.16 and using Hookes law,
Figure 4.16 Elastic settlement of shallow foundation
S
e
=
z
dz =
1
E
s
H
0
p
z
s
p
x
s
p
y
dz
H
0
[4.27]
Where
S
e
= elastic settlement
E
s
= modulus of elasticity of soil
H = thickness of the soil layer
s
= Poisson
s ratio of the soil
p
x
, p
y
, p
z
=
stress increase due to the net applied foundation load in the x, y, and z, directions, respectively
NPTEL ADVANCED FOUNDATION ENGINEERING-I
Theoretically, if the depth of foundation D
f
= 0, H = , and the foundation is perfectly
flexible, according to Harr (1966) the settlement may be expressed as (figure 4.17)
Figure 4.17 Elastic settlement of flexible and rigid foundations
S
e
=
Bq
o
E
s
(1
s
2
)
2
(corner of the flexible foundation) [4.28]
S
e
=
Bq
o
E
s
(1
s
2
) (center of the flexible foundation) [4.29]
Where
=
1
In
1+m
1
2
+m
1
1+m
1
2
m
1
+m In
1+m
1
2
+1
1+m
1
2
1
[4.30]
m
1
= L/B [4.31]
B = width of foundation
L = length of foundation
The values of for various length-to-width (L/B) ratios are shown in figure 4.18. The
average immediate settlement for a flexible foundation also may be expressed as
NPTEL ADVANCED FOUNDATION ENGINEERING-I
Figure 4.18 Values of ,
av
, and
r
equations (28, 29, 32 and 32a)
S
e
=
Bq
o
E
s
(1
s
2
)
av
= average for flexible foundation) [4.32]
Figure 18 also shows the values of
av
for various L/B ratios of foundation.
However, if the foundation shown in figure 17 is rigid, the immediate settlement will be
different and may be expressed as
S
e
=
Bq
o
E
s
(1
s
2
)
r
= (rigid foundation) [4.32a]
The value of
r
for various L/B ratios of foundation are shown in figure 4.18.
If D
f
= 0 and H < due to the presence of a rigid (incompressible) layer as shown in
figure 17,
S
e
=
Bq
o
E
s
(1
s
2
)
[1
s
2
F
1
+1
s
2
s
2
F
2
]
2
(corner of flexible foundation) [4.33a]
And
S
e
=
Bq
o
E
s
(1
s
2
)[(1
s
2
)F
1
+(1
s
2
s
2
)F
2
](corner of flexible foundation) [4.33b]
The variation of F
1
and F
2
with H/B are given in figures 4.19 and 4.20, respectively
(Steinbrenner, 1934).
NPTEL ADVANCED FOUNDATION ENGINEERING-I
Figure 4.19 Variation of F
1
with H/B (based on Steinbrener, 1934
Figure 4.20 Variation of F
2
with H/B (based on Steinbrenner, 1934)
NPTEL ADVANCED FOUNDATION ENGINEERING-I
It is also important to realize that the preceding relationships for S
e
assume that the depth
of the foundation is equal to zero. ForD
f
> 0, the magnitude of S
e
will decrease.
Example 5
A foundation is 1m 2m in plan and carries a net load per unit area, q
o
= 150 kN/m
2
.
Given, for the soil, E
s
= 10,000 kN/m
2
;
s
= 0.3. Assuming the foundation to be
flexible, estimate the elastic settlement at the center of the foundation for the following
conditions:
a. D
f
= 0; H =
b. D
f
= 0; H = 5 m
Solution
Part a
From equation (29)
S
e
=
Bq
o
E
s
(1
s
2
)
For L/B = 2/1 = 2, from figure 18, 1.53, so
S
e
=
(1)(150)
10,000
(1 0. 3
2
)(1.53) = 0.0209 m = 20.9 mm
Part b
From equation (33b)
S
e
=
Bq
o
E
s
(1
s
2
)[(1
s
2
)F
1
+(1
s
2
s
2
)F
2
]
For L/B = 2 and H/B = 5, from figures 19 and 20, F
1
0.525 and F
2
0.06
S
e
=
(1)(150)
10,000
(1 0. 3
2
)[(1 0. 3
2
)(0.525) +(1 0.3 2 0. 3
2
)(0.06)] =
0.007 m = 7.0 mm
ELASTIC SETTLEMENT OF FOUNDATION ON SATURATED CLAY
Janbu et al. (1956) proposed an equation for evaluating the average settlement of flexible
foundations on saturated clay soils (Poissons ratio,
s
= 0.5). For the notation used in
figure 4.21, this equation is
NPTEL ADVANCED FOUNDATION ENGINEERING-I
Figure 4.21 Values of A
1
and A
2
for elastic settlement calculation-equation (34) (after
Christian and Carrier, 1978)
S
e
= A
1
A
2
q
o
B
E
s
[4.34]
Where A
1
is a function of H/B and L/B and A
2
is a function of D
f
/B
Christian and Carrier (1978) modified the values of A
1
and A
2
to some extent, as
presented in figure 21.
SETTLEMENT OF SANDY SOIL: USE OF STRAIN INFLUENCE FACTOR
Settlement of granular soils can be evaluated by use of a semi-empirical strain influence
factor (figure 4.22) proposed by Schmertmann and Hartman (1978). According to this
method, the settlement is
NPTEL ADVANCED FOUNDATION ENGINEERING-I
S
e
= C
1
C
2
(q q)
I
z
E
s
z
z
2
0
[4.35]
Figure 4.22 Elastic settlement calculation by using strain influence factor
Where
I
z
= strain influence factor
C
1
= a = 1
0.5[/( )]
2
= r =
1 +0.2( /0.1)
=
=
The variation of the strain influence factor with depth below the foundation is shown in
figure 22a. Note that, for square or circular foundations,
= 0.1 = 0
= 0.5 =
1
= 0.5
= 0 =
2
= 2
Similarly, for foundation with / 10,
= 0.2 = 0
NPTEL ADVANCED FOUNDATION ENGINEERING-I
= 0.5 =
1
=
= 0 =
2
= 4
Where
= =
For values of / between 1 and 10, necessary interpolations can be made.
To use equation (35) first requires evaluation of the approximate variation of he modulus
of elasticity with depth (figure 4.22). This evaluation can be made by using the standard
penetration numbers or cone penetration resistances. The soil layer can be divided into
several layers to a depth of =
2
, and the elastic settlement of each layer can be
estimated. The sum of the settlement of all layers equals
, Schmertmann (1970)
provided a case history of a rectangular foundation (Belgian bridge pier) having L = 23 m
and B = 2.6 m and being supported by a granular soil deposit. For this foundation we may
assume that / 10 for plotting the strain influence factor diagram. Figure 4.23 shows
the details of the foundation along with the approximate variation of the cone penetration
resistance,
, with depth. For this foundation [equation (35)], note that
Figure 4.23 Variation of
below the foundation
NPTEL ADVANCED FOUNDATION ENGINEERING-I
= 178.54 /
2
= 31.39 /
2
1
= 1 0.5
= 1 (0.5)
31.39
178.5431.39
= 0.893
2
= 1 +0.2
0.1
For = 5
2
= 1 +0.2
5
0.1
= 1.34
The following table shows the calculation of (
2
0
in conjunction with figure
4.23.
Layer ()
(/
2
)
(/
2
)
to the
center of
the layer
(m)
at the
center of
the layer
(
) (
2
/
)
1 1 2,450 8,575 0.5 0.258 3.00
10
5
2 1.6 3,430 12,005 1.8 0.408 5.43
10
5
3 0.4 3,430 12,005 2.8 0.487 1.62
10
5
4 0.5 6,870 24,045 3.25 0.458 0.95
10
5
5 1.0 2,950 10,325 4.0 0.410 3.97
10
5
6 0.5 8,340 29,190 4.75 0.362 0.62
10
5
NPTEL ADVANCED FOUNDATION ENGINEERING-I
7 1.5 14,000 49,000 5.75 0.298 0.91
10
5
8 1 6,000 21,000 7.0 0.247 1.17
10
5
9 1 10,000 35,000 8.0 0.154 0.44
10
5
10 1.9 4,000 14,000 9.45 0.062 0.84
10
5
10.4
= 4
18.95
10
5
a
3.5
[ (40)]
Hence the immediate settlement is calculated as
=
1
2
( )
= (0.893)(1.34)(178.54 31.39)(18.95 10
5
)
= 0.03336 33
After five years, the actual maximum settlement observed for the foundation was about
39 mm.
RANGE OF MATERIAL PARAMETERS FOR COMPUTING ELASTIC
SETTLEMENT
Section 8-10 presented the equations for calculating immediate settlement of foundations.
These equations contain the elastic parameters, such as
. If the laboratory test
results for these parameters are not available, certain realistic assumptions have to be
made. Table 5 shows the approximate range of the elastic parameters for various soils.
Several investigators have correlated the values of the modulus of elasticity,
, with the
field standard penetration number,
and the cone penetration resistance,
, Mitchell
and Gardner (1975) compiled a list of these correlations, Schmertmann (1970) indicated
that the modulus of elasticity of sand may be given by
(/
2
) = 766
[4.36]
NPTEL ADVANCED FOUNDATION ENGINEERING-I
Where
= a
In English units
(. . /
2
) = 8
[4.37]
Table 5 Elastic Parameters of Various Soils
Modulus of elasticity,
Type of soil /
2
/
2
Poissons ratio,
Loose sand 1,500-3,500 10.35-24.15 0.20-0.40
Medium dense sand 2,500-4,000 17.25-27.60 0.25-0.40
Dense sand 5,000-8000 34.50-55.20 0.30-0.45
Silty sand 1,500-2,500 10.35-17.25 0.20-0.40
Sand and gravel 10,000-25,000 69.00-172.50 0.15-0.35
Soft clay 600-3,000 4.1-20.7
Medium clay 3,000-6,000 20.7-41.4 0.20-0.50
Stiff clay 6,000-14,000 41.4-96.6
Similarly,
= 2
[4.38]
Where
=
Schmertmann and Hartman (1978) further suggested that the following correlations may
be used with the strain influence factors described in section 10:
= 2.5
( ) [4.39]
And
= 3.5
( ) [4.40]
Note: Any consistent set of units may be used in equation (38)-(40).
NPTEL ADVANCED FOUNDATION ENGINEERING-I
The modulus of elasticity of normally consolidated clays may be estimated as
= 250 500 [4.41]
And for overconsolidated clays as
= 750 1000 [4.42]
Where
=
CONSOLIDATION SETTLEMENT
As mentioned before, consolidation settlement occurs over time, and it occurs in
saturated clayey soils when they are subjected to increased load caused by foundation
construction (figure 4.24). Based on the one-dimensional consolidation settlement
equations given in chapter 1, we write
Figure 4.24 Consolidation settlement calculation
Where
=
=
1+
NPTEL ADVANCED FOUNDATION ENGINEERING-I
=
= (
, )
So
1+
( )
(From chapter 1) [64]
1+
( )
(From chapter 1) [66]
1+
1+
<
<
)
(From chapter 1) [66]
Where
a
=
= d
=
The procedures for determining the compression and swelling indexes were discussed in
chapter 1.
Note that the increase of pressure, , on the clay layer is not constant with depth. The
magnitude of will decrease with the increase of depth measured from the bottom of
the foundation. However, the average increase of pressure may be approximated by
=
1
6
(
+4
) [4.43]
NPTEL ADVANCED FOUNDATION ENGINEERING-I
where
are the pressure increases at the top, middle, and bottom of the
clay layer that are caused by the foundation construction.
The method of determining the pressure increase caused by various types of foundation
load is discussed in sections 2-7,
can also be directly obtained from the method
presented in section 5.
Example 6
A foundation 1 2 in plan is shown in figure 4.25. Estimate the consolidation
settlement of the foundation.
Figure 4.25
Solution
The clay is normally consolidated. Thus
1+
= (2.5)(16.5) +(0.5)(17.5 9.81) +(1.25)(16 9.81) = 41.25 +3.85 +7.74 =
52.84/
2
From equation (43),
=
1
6
(
+4
)
Now the following table can be prepared (note: = 2 ; = 1 ):
1
= / () /(/2) =
1
2 2 4 0.190 28.5 =
2 2+2.5/2 = 3.25 6.5 0.085 12.75 =
NPTEL ADVANCED FOUNDATION ENGINEERING-I
2 2+2.5 = 4.5 9 0.045 6.75 =
Table 3
Equation (10)
=
1
6
(28.5 +4 12.75 +6.75) = 14.38 /
2
So
=
(0.32)(2.5)
1+0.8
52.84+14.38
52.84
= 0.0465 = 46.5
SKEMPTON-BJERRUM MODIFICATION FOR CONSOLIDATION
SETTLEMENT
The consolidation settlement calculation presented in the preceding section is based on
equations (64, 66, and 68). These equations, as shown in chapter 1, are based on one-
dimensional laboratory consolidation tests. The underlying assumption for these
equations is that the increase of pore water pressure, , immediately after the load
application equals the increase of stress, , at any depth. For this case
(e)
=
1+
(1)
Where
( )
=
(64, 66, 68 1)
(1)
= ( )
= ( 1)
In the field, however, when load is applied over a limited area on the ground surface, this
assumption will not be correct. Consider the case of a circular foundation on a clay layer
as shown in figure 4.26. The vertical and the horizontal stress increases at a point in the
clay layer immediately below the center of the foundation are
(1)
(3)
,
respectively. For saturated clay, the pore water pressure increase at that depth (chapter 1)
is
=
(3)
+ [
(1)
(3)
] [4.44]
NPTEL ADVANCED FOUNDATION ENGINEERING-I
Figure 4.26 Circular foundation on a clay layer
Where
=
For this case
S
=
(
)
(3)
+
(1)
(3)
[4.45]
Thus we can write
( )
=
0
m
v
p
(1)
dz
H
c
0
= A +(1 A)
p
(3)
dz
H
c
0
p
(1)
dz
H
c
0
[4.46]
Where
K
cir
= settlement ratios for circular foundations
The settlement ratio for a continuous foundation (K
str
) can be determined in a manner
similar to that or a circular foundation. The variation of K
cir
and K
str
with A and H
c
/B is
given in figure 4.27. (Note: B = diameter of a circular foundation, and B = width of a
continuous foundation).
NPTEL ADVANCED FOUNDATION ENGINEERING-I
Figure 4.27 Settlement ratios for circular (K
cir
) and continuous (K
str
) foundation
Following is the procedure for determining consolidation settlement according to
Skempton and Bjerrum (1957).
1. Determine the consolidation settlement, S
c(oed )
, using the procedure outlined in
section 12. (Note the change of notation from S
c
.
2. Determine the pore water pressure parameter, A.
3. Determine H
c
/B.
4. Obtain the settlement ratio-in this case, from figure 27.
5. Calculate the actual consolidation settlement:
S
c
= S
c(oed )
settlement ratio [4.47]
This technique is generally referred to as the Skempton-Bjerrum modification for
consolidation settlement calculation.
CONSOLIDATION SETTLEMENT-GENERAL COMMENTS AND A CASE
HISTORY
In predicting the consolidation settlement and the time rate of settlement for actual field
conditions, an engineer has to make several simplifying assumptions. They include the
NPTEL ADVANCED FOUNDATION ENGINEERING-I
compression index, coefficient of consolidation, preconsolidation pressure, drainage
conditions, and thickness of the clay layer. Soil layering is not always uniform with ideal
properties; hence field performance may deviate from the prediction, requiring
adjustments during construction. The following case history on consolidation, as reported
by Schnabel (1972), illustrates this reality.
Figure 4.28 shows the subsoil conditions for the construction of a school building in
Waldorf, Maryland. Upper Pleistocene sand and gravel soils are underlain by deposits of
very loose fine silty sand, soft silty clay, and clayey silt. The softer surface layers are
underlain by various layers of stiff to firm silty clay, clayey silt, and sandy silt to a depth
of 50 ft. before construction of the building began; a compacted fill having a thickness of
8-10 ft was placed on the ground surface. This fill initiated the consolidation settlement
in the soft silty clay and clayey silt.
Figure 4.28 Subsoil conditions for the construction of school building (note: SPT N value
are uncorrected, i.e., after Schnabel, 1972)
To predict the time rate of settlement, based on the laboratory test results, the engineers
made the following approximations:
NPTEL ADVANCED FOUNDATION ENGINEERING-I
a. The preconsolidation pressure, p
c
was 1600 to 2800 lb/ft
2
in excess of the
existing overburden pressure.
b. The swell index, C
s
, was 0.01 to 0.03.
c. For the more compressive layers C
v
0.36 ft
2
/day, and for the stiffer soil layers
C
v
3.1 ft
2
/day.
The total consolidation settlement was estimated to be about 3 in. under double drainage
conditions, 90% settlement was expected to occur in 114 days.
Figure 4.29 shows a comparison of measured and predicted settlement with time, with
indicates that
a.
S
c(observed )
S
c(estimated )
0.47
b. 90% of the settlement occurred in about 70 days; hence t
90(observed )
/
t
90(estimated )
0.58.
The reality rapid settlement in the field is believed to be due to the presence of a fine sand
layer within the Miocene deposits.
Figure 4.29 Comparison of measured and predicted consolidation settlement with time
(after Schnabel, 1972)
NPTEL ADVANCED FOUNDATION ENGINEERING-I
Das könnte Ihnen auch gefallen
- Shallow Foundations Allowable Bearing Capacity & SettlementDokument22 SeitenShallow Foundations Allowable Bearing Capacity & SettlementMansoorNoch keine Bewertungen
- HORIZONTAL SUBGRADE REACTIONDokument1 SeiteHORIZONTAL SUBGRADE REACTIONVegetable BunNoch keine Bewertungen
- Highway Subdrainage Design FHWADokument180 SeitenHighway Subdrainage Design FHWAEliécerNoch keine Bewertungen
- Design of Vertical Bracing Connections For High Seismic DriftDokument12 SeitenDesign of Vertical Bracing Connections For High Seismic DriftvNoch keine Bewertungen
- Dynamic Bearing CapacityDokument38 SeitenDynamic Bearing CapacityEdgar De LeonNoch keine Bewertungen
- Soil Constitutive ModelDokument36 SeitenSoil Constitutive ModelMohamed YousufNoch keine Bewertungen
- Rectangular Spread Footing DesignDokument42 SeitenRectangular Spread Footing DesignJedidiah MelakuNoch keine Bewertungen
- Shallow Foundation 1Dokument48 SeitenShallow Foundation 1Nimas Az-zahra SofaNoch keine Bewertungen
- Assignments and Tutorials - Soil Mechanics - Spring NewDokument42 SeitenAssignments and Tutorials - Soil Mechanics - Spring NewmanthanNoch keine Bewertungen
- Active Vs Passive Earth PressureDokument1 SeiteActive Vs Passive Earth Pressuregeorgeispasoiu100% (1)
- OutputDokument5 SeitenOutputMoch Raka RizkiNoch keine Bewertungen
- Warning ErrorsDokument18 SeitenWarning ErrorsRakesh KRNoch keine Bewertungen
- Geotehcnical AnalysisDokument61 SeitenGeotehcnical AnalysisZakee KazmeeNoch keine Bewertungen
- 26may2014 1Dokument16 Seiten26may2014 1Desai NileshNoch keine Bewertungen
- İsrail Deprem Yönetmeliği EkiDokument18 Seitenİsrail Deprem Yönetmeliği EkiErol Eylemci KaplanNoch keine Bewertungen
- Com624 ManualDokument511 SeitenCom624 ManualNicole CarrilloNoch keine Bewertungen
- C Coek Info - Batter-Pile-DesignDokument11 SeitenC Coek Info - Batter-Pile-DesignMario Colil BenaventeNoch keine Bewertungen
- 12 Substructure - Soil SpringDokument12 Seiten12 Substructure - Soil SpringLea A ManaloNoch keine Bewertungen
- Earthquake Analysis of StructuresDokument42 SeitenEarthquake Analysis of StructuresManmatha KrishnanNoch keine Bewertungen
- Development of A New Family of Normalized Modulus Reduction and Materials Dumping Curves Darendeli PhD-2008)Dokument25 SeitenDevelopment of A New Family of Normalized Modulus Reduction and Materials Dumping Curves Darendeli PhD-2008)omar45Noch keine Bewertungen
- Applied Bearing Pressure For Spread Foundations - FormulaeDokument4 SeitenApplied Bearing Pressure For Spread Foundations - Formulaealex_3_15Noch keine Bewertungen
- Shear Strength of Dam-Foundation Rock Interface PDFDokument4 SeitenShear Strength of Dam-Foundation Rock Interface PDFAdrian Luis Hernandez GarciaNoch keine Bewertungen
- Seismic Earth Pressures Fact orDokument18 SeitenSeismic Earth Pressures Fact orvalerita89Noch keine Bewertungen
- Latihan 1 - Perilaku Struktur Rangka Baja - Firstka Safira - 25019325Dokument17 SeitenLatihan 1 - Perilaku Struktur Rangka Baja - Firstka Safira - 25019325Firstka SafiraNoch keine Bewertungen
- SDM Example 3 Steel SMF PDFDokument30 SeitenSDM Example 3 Steel SMF PDFRicardoMallmaNoch keine Bewertungen
- Allpile WhiteDokument11 SeitenAllpile WhiteKiryaki FrancisNoch keine Bewertungen
- Prediction of Piled Raft Foundation Sett PDFDokument6 SeitenPrediction of Piled Raft Foundation Sett PDFAhmed MohammedNoch keine Bewertungen
- SAFE ManualDokument20 SeitenSAFE ManualMelvin SolisNoch keine Bewertungen
- kmjk07 PDFDokument10 Seitenkmjk07 PDFParamita BhattacharyaNoch keine Bewertungen
- Eccentric Beam Column Connections Ci 2004 138Dokument5 SeitenEccentric Beam Column Connections Ci 2004 138kp21100% (2)
- Structural Dynamics & Earthquake EngineeringDokument34 SeitenStructural Dynamics & Earthquake EngineeringHema Chandra Reddy Karimireddy100% (1)
- Evaluation of Slope Performance Under Earthquake Loading ConditionsDokument13 SeitenEvaluation of Slope Performance Under Earthquake Loading ConditionsFederico MalteseNoch keine Bewertungen
- Shallow and Deep Foundations DR PDFDokument8 SeitenShallow and Deep Foundations DR PDFLleiLleiNoch keine Bewertungen
- FE Modeling of Embedded Cantilever Sheet Pile Retaining WallDokument10 SeitenFE Modeling of Embedded Cantilever Sheet Pile Retaining WalllollazzoNoch keine Bewertungen
- Optimal Location of Piles in Slope Stabilization by Limit AnalysisDokument8 SeitenOptimal Location of Piles in Slope Stabilization by Limit AnalysisIsmaelMartinez100% (1)
- Lecture 3 Columns - Oct 12 - EndDokument70 SeitenLecture 3 Columns - Oct 12 - EndLiam WilliamsNoch keine Bewertungen
- Optimal Deign of Pile FoundationDokument13 SeitenOptimal Deign of Pile FoundationJustin Johnson100% (1)
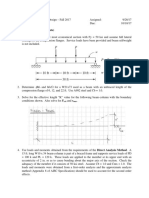
- m4l29 Lesson 29 The Direct Stiffness Method: Beams (Continued)Dokument16 Seitenm4l29 Lesson 29 The Direct Stiffness Method: Beams (Continued)Vitor Vale100% (1)
- AISC DG11 ExamplesDokument7 SeitenAISC DG11 ExamplesMarcel Toruño MendezNoch keine Bewertungen
- Designing compression piles according to Eurocode 7Dokument12 SeitenDesigning compression piles according to Eurocode 7Aniket DNoch keine Bewertungen
- Ecuaciones Wang & ReeseDokument10 SeitenEcuaciones Wang & ReeseMáryuri CriadoNoch keine Bewertungen
- EQuake Forces On Water Retaining StrsDokument4 SeitenEQuake Forces On Water Retaining StrssyakurNoch keine Bewertungen
- ProtaStructure Suite 2016 Whats NewDokument41 SeitenProtaStructure Suite 2016 Whats NewPlacid FabiloNoch keine Bewertungen
- Settle3D Liquefaction Theory Manual v4Dokument58 SeitenSettle3D Liquefaction Theory Manual v4Jamie QuilalaNoch keine Bewertungen
- Generation of Artificial Strong Motion: AccelerogramsDokument19 SeitenGeneration of Artificial Strong Motion: AccelerogramsMarko AdamovićNoch keine Bewertungen
- Plaxis ValidationDokument5 SeitenPlaxis Validationعصام السامرائيNoch keine Bewertungen
- Bilinear Isotropic Hardening BehaviorDokument7 SeitenBilinear Isotropic Hardening BehaviorricardoborNoch keine Bewertungen
- Mat Foundations Engineering Design and AnalysisDokument80 SeitenMat Foundations Engineering Design and AnalysisSabrina Imloul100% (3)
- Pywall v3 Validation NotesDokument17 SeitenPywall v3 Validation NotesXuejian LiuNoch keine Bewertungen
- Soil Structure InteractionDokument16 SeitenSoil Structure InteractionEmad Ahmed Khan67% (3)
- Investigation of the Chirajara Bridge CollapseVon EverandInvestigation of the Chirajara Bridge CollapseNoch keine Bewertungen
- Lecture Notes on Reinforced Concrete DesignVon EverandLecture Notes on Reinforced Concrete DesignNoch keine Bewertungen
- Numerical Methods and Implementation in Geotechnical Engineering – Part 1Von EverandNumerical Methods and Implementation in Geotechnical Engineering – Part 1Noch keine Bewertungen
- Condo QuestionnaireDokument5 SeitenCondo QuestionnaireMansoorNoch keine Bewertungen
- Structural Engineering Practice ProblemsDokument2 SeitenStructural Engineering Practice ProblemsMansoorNoch keine Bewertungen
- Angle EmbedDokument1 SeiteAngle EmbedMansoorNoch keine Bewertungen
- Column AnalysisDokument2 SeitenColumn AnalysisMansoorNoch keine Bewertungen
- Changes To ACIDokument4 SeitenChanges To ACIMansoorNoch keine Bewertungen
- Executive Summary of The RepaortDokument1 SeiteExecutive Summary of The RepaortMansoorNoch keine Bewertungen
- 0416 001Dokument5 Seiten0416 001MansoorNoch keine Bewertungen
- 0506 001Dokument1 Seite0506 001MansoorNoch keine Bewertungen
- Novel Use of Buckling-Restrained Braces in Precast Concrete Frames, PCI Journal Sep-Oct 2017Dokument1 SeiteNovel Use of Buckling-Restrained Braces in Precast Concrete Frames, PCI Journal Sep-Oct 2017MansoorNoch keine Bewertungen
- Technical Information ASSET DOC LOC 1555609Dokument2 SeitenTechnical Information ASSET DOC LOC 1555609MansoorNoch keine Bewertungen
- 10Dokument1 Seite10MansoorNoch keine Bewertungen
- Engr600 Quiz - 3Dokument4 SeitenEngr600 Quiz - 3MansoorNoch keine Bewertungen
- Executive Summary of The RepaortDokument2 SeitenExecutive Summary of The RepaortMansoorNoch keine Bewertungen
- For Example of One of The IntegralsDokument3 SeitenFor Example of One of The IntegralsMansoorNoch keine Bewertungen
- OLS - Report - Certification of 10T Obelix Lifting Clutch PDFDokument2 SeitenOLS - Report - Certification of 10T Obelix Lifting Clutch PDFMansoorNoch keine Bewertungen
- CE 631 Advanced Steel Design Homework 5Dokument2 SeitenCE 631 Advanced Steel Design Homework 5MansoorNoch keine Bewertungen
- Quiz 3 - Finite ElementDokument1 SeiteQuiz 3 - Finite ElementMansoorNoch keine Bewertungen
- Standard Girder PDFDokument1 SeiteStandard Girder PDFMansoorNoch keine Bewertungen
- Summary of 2D Constant Strain ElementDokument3 SeitenSummary of 2D Constant Strain ElementMansoorNoch keine Bewertungen
- SWI 100 QueryDokument1 SeiteSWI 100 QueryMansoorNoch keine Bewertungen
- Engr 636-3 PDFDokument3 SeitenEngr 636-3 PDFMansoorNoch keine Bewertungen
- HW4 Problem 1Dokument12 SeitenHW4 Problem 1MansoorNoch keine Bewertungen
- Movie LetterDokument2 SeitenMovie LetterMansoorNoch keine Bewertungen
- 2881 001Dokument1 Seite2881 001MansoorNoch keine Bewertungen
- ENGR 636 Tuesday 3/14: 1. Review HW 3 SolutionDokument3 SeitenENGR 636 Tuesday 3/14: 1. Review HW 3 SolutionMansoorNoch keine Bewertungen
- 3531 001Dokument1 Seite3531 001MansoorNoch keine Bewertungen
- 3517 001Dokument1 Seite3517 001MansoorNoch keine Bewertungen
- 2762 001Dokument12 Seiten2762 001MansoorNoch keine Bewertungen
- Homework 4, EnGR 636Dokument1 SeiteHomework 4, EnGR 636MansoorNoch keine Bewertungen
- Direct and Min Total PE FormulationDokument12 SeitenDirect and Min Total PE FormulationMansoorNoch keine Bewertungen
- Tube Fitting Hoke Gyrolok CatalogueDokument56 SeitenTube Fitting Hoke Gyrolok CatalogueGorbyNoch keine Bewertungen
- Metals KS3 4 Iron and Aluminium Extraction Methods Info SheetDokument5 SeitenMetals KS3 4 Iron and Aluminium Extraction Methods Info SheetHappy NthakomwaNoch keine Bewertungen
- Bachmann Process For RDXDokument4 SeitenBachmann Process For RDXjoshuaericksonNoch keine Bewertungen
- Thermal Issues in Materials Processing: Yogesh JaluriaDokument14 SeitenThermal Issues in Materials Processing: Yogesh JaluriarahulNoch keine Bewertungen
- Binary Phase DiagramsDokument60 SeitenBinary Phase DiagramsmaryzeenNoch keine Bewertungen
- Spray Drying Technique of Fruit Juice Powder: Some Factors Influencing The Properties of ProductDokument10 SeitenSpray Drying Technique of Fruit Juice Powder: Some Factors Influencing The Properties of ProductNanda AngLianaa KambaNoch keine Bewertungen
- Avogadro's Law ExplainedDokument18 SeitenAvogadro's Law ExplainedNico Van De CasteeleNoch keine Bewertungen
- Merichem Process Technologies Brochure (English)Dokument31 SeitenMerichem Process Technologies Brochure (English)Walid Fattah100% (3)
- Problems: CHEM1020Dokument45 SeitenProblems: CHEM1020Ahmed AliNoch keine Bewertungen
- Combat Rising Damp and Moisture IngressDokument2 SeitenCombat Rising Damp and Moisture IngressESwar KarthikNoch keine Bewertungen
- Lesoon Equipment Catalogue 2015Dokument28 SeitenLesoon Equipment Catalogue 2015Jason PerezNoch keine Bewertungen
- SKAB4022 Short Proposal - Nur Amalina Binti IshakDokument16 SeitenSKAB4022 Short Proposal - Nur Amalina Binti Ishakazhar ahmadNoch keine Bewertungen
- ASTM C33 02a Concrete AggregatesDokument11 SeitenASTM C33 02a Concrete AggregatesJanice Tatiana Alva DelgadoNoch keine Bewertungen
- Checklist NOM-251-SSA1-2009Dokument14 SeitenChecklist NOM-251-SSA1-2009ScribdTranslationsNoch keine Bewertungen
- Expt 1-Alkalinity of Water SampleDokument4 SeitenExpt 1-Alkalinity of Water SampleAbdul RehmanNoch keine Bewertungen
- Adsorption of Flouride Using Nanoparticles of Aluminium OxideDokument15 SeitenAdsorption of Flouride Using Nanoparticles of Aluminium OxideIsa musaNoch keine Bewertungen
- Calculation Sheet: Design CodeDokument1 SeiteCalculation Sheet: Design CodeCak AndiNoch keine Bewertungen
- 2017 Review Silane Mechanism AdhesionDokument16 Seiten2017 Review Silane Mechanism AdhesionDarell Josue Valdez AquinoNoch keine Bewertungen
- Xdcixz2u1wgmgwoavm1gwjvasvj G9vcs39xeb2vi34mccaalbrb7asbodbb3wsn6ujqmqwv8twty Qf4a3jjeqwik Af6q 4mhxyludDokument2 SeitenXdcixz2u1wgmgwoavm1gwjvasvj G9vcs39xeb2vi34mccaalbrb7asbodbb3wsn6ujqmqwv8twty Qf4a3jjeqwik Af6q 4mhxyludAbou Tebba SamNoch keine Bewertungen
- Sample Questions - Chapter 2Dokument5 SeitenSample Questions - Chapter 2Rasel IslamNoch keine Bewertungen
- CV of Dr. Janakarajan RamkumarDokument20 SeitenCV of Dr. Janakarajan RamkumarAnonymous fgrTyKxxsLNoch keine Bewertungen
- Mech Vi Non Traditional Machining (10me665) NotesDokument45 SeitenMech Vi Non Traditional Machining (10me665) Notesnikhil0% (1)
- Pile Jacking FullTextDokument223 SeitenPile Jacking FullTextGeorge Ardianda CrNoch keine Bewertungen
- Resistência Da Cor Ao Calor Prensagem A Quente - AATCC 133-2010Dokument2 SeitenResistência Da Cor Ao Calor Prensagem A Quente - AATCC 133-2010raissaNoch keine Bewertungen
- BPC - BG HD 7000fDokument1 SeiteBPC - BG HD 7000fSLKM Engineering & ConsultantsNoch keine Bewertungen
- Chondroitin sulfate sodium analytical methods guideDokument3 SeitenChondroitin sulfate sodium analytical methods guideAchmad LatiefNoch keine Bewertungen
- Design of Offshore StructuresDokument29 SeitenDesign of Offshore StructuresJOSE PRASOBH..JNoch keine Bewertungen
- IES Mechanical Engineering Paper II 2013 PDFDokument20 SeitenIES Mechanical Engineering Paper II 2013 PDFBalvinderNoch keine Bewertungen
- Learner'S Packet No.1 Quarter 1: Name of Student: Learning Area/Grade Level: Tle-He-Cookery-Grade 9 Date: Activity TitleDokument10 SeitenLearner'S Packet No.1 Quarter 1: Name of Student: Learning Area/Grade Level: Tle-He-Cookery-Grade 9 Date: Activity TitleSalgie MasculinoNoch keine Bewertungen
- Rigid Pavement: Postgraduate Studies Highways EngineeringDokument15 SeitenRigid Pavement: Postgraduate Studies Highways EngineeringHANAN HUSSNoch keine Bewertungen