Bca Experiments

EXPERIMENT NO: DATE:
Department of BCA and B.Sc(CS) ,KSCD.

CAPACTIANCE OF CONDENSER BY
CHARGING AND DISCHARGING

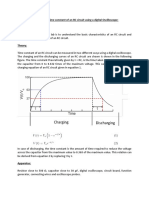
AIM: To determine the time constant of the resistance capacitance series circuit by
charging and discharging characteristics. From the results find the capacitance of a
capacitor.

APPARATUS: High resistance (R), Electrolytic capacitor (C), accumulator charge
and discharge key, tap key, digital stop watch and DMM, bread board and
connecting wires.

INTRODUCTORY INFORMATION: Capacitor in series with resister may be used
in electronic or electronic circuit to control the time required for a current or
voltage to reach a specified value. Operation of this circuit is circuit given below.
R and C are connected in series when we just start charging capacitor, charge on
capacitor is such that potential difference across capacitor Vc is zero but charging
current is maximum as charge starts collecting on C, Vc starts increasing but both
charging current and the potential difference across resistor V
R
starts decreasing at
progressively decreasing rate C:
( E = V
R
+ V
c
), Vc is given by Vc =E ( 1 e
- t/RC
) where RC = T = Time constant
of the circuit Vc = Voltage across C at time.

NATURE OF GRAPH:

CIRCUIT DIAGRAM
: -

E-transistor power supply (5V)
C = Electronic Capacitor of Capacitance
R = 320 K
DMM Digital millimeter.
C & D Charge and discharge key
T - Tap key

OBSERVATIONS: -
1. Resistance used R = 320 k.
3. theoraticaltical values of time constant T = RC sec



Table: 1 Table: 2
Charging curve Discharging curve
Sl.
no
Charging
time t
Sec
Voltage
across
capacitor
V. Volt

Obs
No.

Discharging time
t
sec
Time Voltage across C
Vc Volt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20


When discharging key is pressed battery is cut of capacitor is short circuited
through R. Hence it starts discharging Voltage value decreases exponentially.
Progressively decreasing value of the Voltage Vc is given by Vc = E(
e t/Rc
)
Where the product RC is called time constant and t is the time at which voltage
across C is Vc
The time required to rise the voltage across the capacitor to 63. 2 % of the
maximum applied Voltage is called the time constant of Rc circuit
:: Time constant = T = Rc
It is also the time during which the Voltage across the capacitor falls to 37 % of its
initial maximum value.
Equation Vc = E( e
t/ RC
)
Represents the
decreasing curve.

PROCEDURE: For Table I
Set up the circuit as shown in the figure set the range selection. Switch on
DMM charge the capacitor for s by pressing C and D lay to the position and
simultaneously start the stop watch. After 5 release the C & D key and record Vc
on DMM and time t. Discharge the capacitor fully by closing the tap key T for few
seconds. Now carry out the procedure for time t = 10, 20, 25, ___ until capacitor
voltage reaches the emf of battery

CALCULATION:
Time constant for charging curve = T1
Time constant for discharging curve = T2
Time constant =( T1+T2)/2=
Capacitance of condenser C = T/R=

(Note: for each value of t the capacitor should be discharged before charging).
Tabulate the observations and then plot the charging curve from the charging curve
determine the time constant the time value corresponding Vc = 0.632 V max is the
time constant T.

For Table II:
First charge the capacitor to the battery voltage by pressing C & D key to
position 1 and holding in this position for about 2 to 3 minutes. Then immediately
press C and D key to the position 2 and simultaneously start the stopwatch. Allow
the capacitor to discharge for 5 After 5 second release the key and record Vc and
time. Again charge the capacitor back to its E value and repeat the procedure as
described already for time interval mentioned in the chart. Record the observations
and plot-discharging curve. From this curve determine the time constant. Time for
which curve Vc = 0.37 Vmax is the time constant.

PROCEDURE:

RESULT:
Time constant of the resistance capacitance series circuit=
Capacitance of condenser =

RESONANCE IN LCR CIRCUIT

AIM ; Set up series and parallel resonance Circuit with the resonance frequency fo
= 2250.5 H Study the response of circuit as a function of frequency. Determine the
band width, resonant frequency & quality factor of the circuit take R = 50 , L =
50 mH and C = 0.1 F

APPARATUS : - Inductor, Capacitor, resistance box, Plug key, frequency
generator, multimeter.

FORMULA:-(i) f
o
= resonant frequency =
Here L= 50mH = 50 * 10
3
Hz
C= 0.1 F = 0.1* 10
-6
F
R = 50

(ii) Band Width = f = f
2
f
1

f
2
Upper half power frequency
f
1
Lower half power frequency

(iii) Quality factor
Here fo = Resonant frequency determined by experimental method
f = band width

THEORY: - The property of cancellation of reactance when inductive and
capacitive reactance in series or the cancellation of susceptance when inductor and
capacitor are in parallel is called as resonance.


CIRCUIT DIAGRAM FOR SERIES LCR CIRCUIT:

AFG Audio frequency generator
L Inductor = 50 mH
C Capacitor = 0.1 F
R Resistor = 50

NATURE OF GRAPH:

From graph ,
Fo resonant frequency
I max = mA

There are two types of resonance Circuits
1) LCR series resonance
2) LCR Parallel resonance

1) LCR Series resonance when LCR are in series the effective impedance is a
function of frequency
Zeff = effective impedance
Zeff = R + J (wL 1/Wc)
At certain frequency fo, the effective impedance drops to minimum &
current in the circuit is of maximum value the frequency at which effective
impedance drops to minimum or current in the circuit maximum is called resonant
frequency. The variation of the current in the circuit with respect to frequency of
current applied voltage is shown in the graph the line drawn parallel to frequency
axis, from a point corresponding to current value 0.707. I max on the current
frequency graph intersects is called lower half & second intersect is called upper
half frequency.

2) LCR Parallel resonance : - When LCR are connected in Parallel the effective
impedance zeff raises current in the circuit drops to minimum. Nature of variation
of impedance of the circuit with the frequency as shown in the graph. The frequency
at which Zeff raises to maximum value & current drops to minimum value is called
resonant frequency fo.


TABULAR COLUMN: -
SL. no Frequency f in (Hz) Current I in (mA)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

In this case fo = At resonance frequency the effective impedance of
circuit. Zeff = Zmax =
In case of parallel resonance circuit the band width is defined as the difference
between the frequencies corresponding to two points on either side of resonant
frequency, where value of the impedance drops to 0.707 times the maximum value
of impedance.

Band width - f = f
2
f
1

Quality factor
fo =

CIRCUIT DIAGRAM; - LCR PARALLEL RESONANT CIRCUIT

AFG - Audio frequency generator
L Inductor 50 mH
C Capacitor 0.1 F
R Resistor 50
K Plug Key

NATURE OF GRAPH: -

OBSERVATION: -
1) Vin =
2) Zmax =

CALCULATION: -
1) Band width, f = f
2
f
1
=
2)Quality Factor,

TABUALR COLUMN: -
SL. No Frequency f (Hz) Current I (mA) Impedance Z = V
in

I

From graph : for parallel
Zmax =
INVERTING AND NON INVERTING AMPLIFIER

AIM: -
1) Set up an Op- amp IC 741 as inverting amplifier having an absolute value of
gain equal to 10 compare the observed voltage to the theoretical values of the
output for various input voltages sketch the input & output wave forms for
any one of output.
2) Set up an Op amp IC 741 as non inverting amplifier having an absolute
value of gain equal to 11 compare the measured output voltages with the
theoretical value of output for various input values. Sketch the input &
output voltages wave forms for any one of inputs.

APPARATUS:- Op amp IC 741, Resistors, audio frequency generator,
breadboard, CRO, Connecting wires, DC Power Supply.

THEORY: - The operational amplifier is most commonly termed as Op amp. Due
to its use in performing mathematical operations, it has been given the name
operational amplifier. Because of their low cost, small size, flexibility Op amp are
in the field of process control, communications, computers, power and signal
sources delays & measuring systems.
In linear applications output voltage of the amplifier varies linearly wire the
input voltages off their exists a phase difference of 180
o
between input and part of
output which is feedback. The feedback maker the gain of the circuit stable, noise
distortion is less, higher band width and improved output & input impedance values
study of such an inverting amplifier gain properly to the purpose of experiment in
case of non inverting amplifier (gain) there is no phase difference between input &
output quantities.

CIRCUIT DIAGRAM: -
Inverting amplifier.

Non Inverting amplifier

AFG audio frequency generator
R1 Resistor = 10 K
R2 10 K
IC 741 Op amplifier.

Inverting amplifier:
Amplifier which provides a phase difference of 180
o
between input & output
is called inverting amplifier.
Closed loop gain of gain of the inverting amplifier
= V
o
/ Vin
where
V
o
output voltage
Vin input voltage
The 3 terminals of Op-amp is at potential Vin. Hence the potential of 2
terminal of Op-amp is also equal to Vin
:. VA = VB = Vin
VA = Potential of terminal 2 of Op-amp
VB = Potential of terminal 3 of Op-amp
For outside I = V
o
-V
A

R
2

I = V
o
-Vin
R
2

At inverting terminal 2 of Op-amp
I = V
A
-O = Vin (: V
A
= Vin)
R
1
R
1

Entire current passes through R
2

VO V
in
= V
in

R
2
R
1

V
O
= V
in
+ V
in
= V
in
(R
1
+ R
2
)
R
2
R
2
R
1
R
1
R
2
V
O
= R
2
(R
1
+ R
2
) = (R
1
+ R
2
)
Vin R1 R
2
R
1

:. V
O
/V
in
= gain of amplifier
= 1+R
2
/R
1


NATURE OF GRAPH OF INVERTING AMPLIFIER

NON INVERTING AMPLIFIER

Here +ve sign of gain indicates that the input & output are in phase in case of
non inverting amplifier gain will be always greater than 1.
The terminal 3 of Op-amp is ground therefore from concept of virtual
ground; the terminal 2 is also at ground potential.

OBSERVATIONS & TABULAR COLUMNS

Inverting amplifier
R
1
= . R
2
=
Gain on amplifier = - R2/R1 =
Frequency =

Input voltage V
in
(volt) Output voltage V
o
in
volt
Calculated output voltage Vo
= - Vin R
2
/R
1

Non Inverting amplifier
R
1
= R
2
= gain = 1+(R
2
/R
1)
=2

Input voltage V
in
(volt) Output voltage V
o
volt Calculated output voltage
Vo = -Vin ( 1+R
2
/R
1
)


I = V
in
- VA
R

Vin input voltage
VA potential of terminal 2 of Op-amp ground potential = 0
:. I = V
in
/
R
on output side
R = V
A
V
O
O Vo Output voltage
R V
A
potential at terminals
R = V
O
/R
Entire current flowing through R1, passes through
R2 :. Vin = VO
R
1
R
2

VO/Vin = -R2/R1 gain of amplifier here Ve sign denotes that input & output are
out of phase.
Here gain can be greater, less than or equal to 1, depending on values of R
1
&
R
2
Non inverting amplifier where in input & output are in phase is called non-
inverting amplifier gain V
O
/V
in.

INDENTIFICATION AND MEASUREMENT OF
R ,L AND C IN A BLACK BOX

AIM: - To identify the terminals of R, L and C to determine the values of R, L and
C in the black box.

APPARATUS: - Black box containing R, L and C, Audio Frequency Generator
(AFG) AC voltmeter, bread board connecting wires, resistance box, DC and AC
source etc.

THEORY: - Black box is a box that contains Resister; Inductor and Capacitor with
one end of the each connected to one common terminal of black box and other ends
to each are connected to different terminals of the black box. Therefore given black
box has four terminals A, B, C, and D

CIRCUIT DIAGRAM:

Observation: -

Tr. No Measure Resistance across Resistance
1 AB
2 AC
3 AD
4 BC
5 BD
6 CD


INFERENCE: -

1. _____________ Terminal is common for R =
2. _____________ Terminal is one end of the capacitor
3. Resistance across ________&_______ terminals is maximum
4 R and L are in series between terminal ___________and ____________
5. The terminal __ is node for components R, L and C
6. Capacitor is present between _______and _______terminals.
7. Resitance is present between _______and
_______terminals
8. Inductor is present between _______and _______terminals

CIRCUIT DIAGRAM II: -

To determine terminals of L and R, and also to determine values of C L and
R.
AFG Audio frequency generator
R - Resistance box (0-1000)
V
1
- dc voltmeter (0-10V)
V
2
- dc voltmeter (0-5V) BB Black box with terminals A, B, C & D

OBSERVAITON: -

1. Resistance R
L
in resistance box R =
2. Frequency of alternating voltage input =
3. Nodal terminal is ___B
4. Probe is connected to ________terminal of black box
Given : B is a nodal terminal.

Payable RL Voltmeter reading Iac = V
1
-V
2

/
R

A
Z = V
2
/
Iac
Mean Z
Bet m
V
1
Volt
Bet N
V
2
Volt
V1-V2
Volt
A
AB

B
BC

C
BD

CALUCATION: -
C = = __________F
L= =______________mH

INFERENCE: -

1. Nodal terminal is __
2. R and L are in series between __ and__ terminals
3. Resistance across BD determined by II multimeter ___
4. Resistance across XD determined by part II =______
: Resistance across BD determined by multimeter Resistance across XD
determined by Part II
: Resistance is present in between __ & __ terminals .
5. Capacitor is present between __ and __ terminals
: Inductor must be between __ & __ terminals
: R, L and C Connections in black box are of type.


ZENER DIODE AS A VOLTAGE REGULATOR

Aim:
To determine Zener diode as a voltage regulator to provide a constant voltage from
a source whose voltage may vary over sufficient range.

Apparatus:
Zener Diode, battery,resistor,resistance box,voltmeter,plug key, connecting wires.

THEORY:
Zener Diode of Zener Voltage Vz is reverse connected across the load RL across
which constant output is derived. The series resistance R absorbs the output voltage
across fluctuations so as to maintain constant voltage across the load. When an
input DC source is applied to the Zener diode, the output voltage will be the same as
the input voltage. When the input voltage exceeds the breakdown voltage of the
Zener diode, the output voltage remains constant even when the input voltage is
increased. Hence Zener diode acts as a voltage regulator.

CIRCUIT DIAGRAM:

Ba - Battery (0 V to 20 V) R - Resistor (220 )
RL - Resistance Box V - Voltmeter
K - Plug Key

NATURE OF GRAPH:


TABULAR COLUMN:

LOAD REGULATION

INPUT VOLTAGE V
in
=

Resistance R
L
(ohm) Voltage across Zener Diode V
Z
(volts)


LINE REGULATION

Load R
L
=

Input voltage V
in
(volts) Voltage across Zener Diode V
Z
(volts)

Procedure:

1. Connections are made as shown in the circuit diagram.
2. Supply an input voltage of 10 V.
3. Unplug 100 resistance from the resistance box. Note down the corresponding
voltmeter reading.
4. Continue the procedure for 200 , 300 , 10 K and note down the
corresponding voltmeter reading.
5. Unplug 10 K of resistance from the resistance box
6. Supply an input voltage of 1 V and note down the corresponding voltmeter
reading.
7. Continue the procedure for 2 V, 3 V,.15 V and note down the corresponding
voltmeter reading.
8. Plot the graph of RL v/s Vz and Vin v/s Vz.


ENERGY GAP OF A SEMI CONDUCTOR

THERMISTOR

AIM: Determine the resistance of the thermistor at various temperatures. Plot the
characteristic graph log
10
R (1/T) and hence determine the energy gap of the
given thermistor.

THEORY: Thermistor is temperature sensitive resistor. Its thermal resistance is
related to the body temperature. Thermistor is made up of Germanium, Nickel, and
Manganese. These thermistors are available in different shapes and size. They are in
the form of beads, rods and discs. The compound employed will determine whether
the device has +ve or ve temperature coefficient. Thermistors of resistance ranging
from 1 200 at 800 k are available.
The energy required to transfer an electron from valence bond to conduction
band is called energy gap. The conductivity J of a semiconductor is given by = ze(-
Eg/
2kt) *
e
((e + n)
where I > Z is total number of carriers per unit value of
semiconductor in conduction band and value band
ii) Eg: Energy gap
iii) K: Boltzmanns constant = 8. 62*10-5 eV/ k
iv) e: Electronic charge
v) e = Mobility of electrons
vi) T = Temperature in Kelvin
vii) n = mobility of holes
viii) = Conductively = 1/s
ix) S = Specific resistance
OBSERVATIONS:
Room temperature =
Applied Voltage V =


Tabular Column:
Obs No Temp t
in C
0

Abs temp
T = t + 273k
Current I
in mA
Resistance
R = V/ I
Log R
1/ T (sec
-1
)
1
2
3
4
5
6
7
8
9
10
11
12
13

Nature of graph:

CALCULATION:
Energy gap:- m * 4.606 * 8.62 * 10
-5


SEMICONDUCTOR DIODE

AIM: Obtain current against voltage characteristic for semiconductor diode under
forward bias and condition from the characteristic curves determine important
parameters related to diode.

APPARATUS: Battery, milliammeter, Voltmeter, diode, rheostat, plug key.

THEORY: Forward bias:
When a positive terminal of a dc source is connected to the P side and
negative terminal to the n-side of the PN junction diode it is said to be forward
biased. Forward bias Voltage opposes the potential barriers at the depletion layer.
As forward bias voltage is (V
F
) increases from 0 to the battery potential value
initially there will not be flow of forward current later forward current slowly
increases. When forward voltage is more than barrier potential effect of barrier
potential becomes too less. In this region as the forward potential increases forward
current also increases therefore whenever diode is forward, resistance of diode is
small.

CIRCUIT DIAGRAM: (Forward bias)

D Diode, Ba Battery, Rh Rheostat, MA Milliammeter (0-25 mA),
V-voltmeter, K Plug key, A Anode, K Cathode

NATURE OF GRAPH: -

PROCEDURE: Forward bias
1) Connections are made as shown in the circuit diagram.
2) Note down the readings of the V
f
with corresponding I
f
until it reaches
to its maximum.
3) Plot the graph of V
f
versus I
f
.
4) Find the slope of the graph and calculate if by using the formula,

Where, R
F
is the forward resistance.

HALF WAVE RECTIFIR

AIM: To study half wave rectifier and calculate ripple factor and percentage of
regulator.

APPARATUS: Semiconductor diode, transformer, plug key, Variable Resistor,
milliammeter, dc voltmeter and AC voltmeter.

THEORY: It consists of a transformer which steps down from the power mains to
very low voltage and the circuits consist of load resistance Rc and the diode D.
The Voltage induced in the secondary of the transformer is passed to the
diode the diode is forward biased for the positive peak value and the diode conducts
and the current flows through the load. During Ve half cycle the diode is reversed
bias and it does not conduct and current flows through the load. In this way the ac
voltage is converted into dc voltage.

CIRCUIT DIAGRAM:

T Transformer Rh variable resistor
D Semiconductor V
ac
ac Voltmeter
K Plug key V
dc
dc - Voltmeter
C Capacitor = 0.1mf A ammeter
OBSERVATION: -

When the plug key is open, then
I
max
=
V
dc
=
V
ac
=
Ripple factor =

TABULAR COLUMN: -

SL.NO Iz (mA) Vdc (V) Vac (V)

ripple factor

ripple factor =

% voltage

regulation =

OBSERVATION : - (Forward bias)

TABULAR COLUMN: -

Obs No Voltmeter reading
V
f
Volt
Milliammeter
Reading I
f
(mA)

PROCEDURE:
1) Connections are done as shown in the circuit diagram.
2) Keep the plug key (k) open, switch on the Ac mains note down Vdc and Vac.
3) The plug key is closed and the reading of I, Vac and Vdc are noted down for
corresponding readings.
4) With the increase of Rheostat it is varied for different readings of I, Vac are
noted.
5) After completion of taking the readings calculate the ripple factor using formula.

6) Calculate the percentage of regulator using the formula.

Where, V
NL
is the Voltmeter reading when no current is passed through it.

CALCULATIONS: -


RC PHASE SHIFT OSCILLATOR

AIM: - Set up the RC Phase Shift oscillator using transistor and determine the
frequency of alternating voltage developed by Oscillator.

FORMULA: - Frequency of alternating voltage developed by oscillator

Hz

Where, Rc= Collector resistance
R= Resistance in phase shift network
C= Capacitance of capacitor in phase shift oscillator.

THEORY: - In RC Phase Shift oscillator, three RC Sections are used to provide 180
degree phase shift and the remaining 180 degree phase shift is provided by the transistor.
Therefore there is a total 360 degree phase shift.

CIRCUIT DIAGRAM:


TABULAR COLUMN: -

Theoretical value of frequency Measured value of frequency

Sr
no
Capacitance
C(F)
Resistance
R(k)
Frequency(F) Length
of one
wave
A(div)
Time base
B(s/div)
Time
period
T=A*B
sec
Frequency
F=1/T Hz

WAVEFORM:-

PROCEDURE:-
1] Connections are made as shown in the circuit diagram.
2] Adjust the potentiometer to obtain a stable wave form on CRO. 3] Find the time
period T.
4] Then calculate the frequency f= 1/ T Hz.
5] Compare this value with the theoretical value, repeat the experiment for different
values of R.

CONCLUSION: -


COLPITTS OSCILLATOR

AIM: - Set up Colpitts Oscillator using transistor determine the frequency of oscillating
for various set of capacitors C1 & C2.

APPARATUS: - BC547, NPN Transistor, resistor, capacitors, power supply.

FORMULA: - Frequency of Oscillator

Where, L=inductance=38.95 H= 38.95 x 10
-6
H

C=capacitance= .. microfarads

THEORY: - The tank circuit provides 180-degree phase shift and the amplifier provides
180 degree. Thus, there is a total phase shift of 360-degree. Hence the feedback is +ve.
The frequency of oscillation is,

CIRCUIT DIAGRAM:


TABULAR COLUMN:
Sl no Theoretical value of frequency Measured value of frequency

Capacitor
C
1
(F)

C=(C
1
*C
2
)/
(C
1
+C
2
)
In F

F=1/2LC
MHz

Length of
one wave
(div)

Time base
B (ms/div)

Time period
AB
Sec
-1

Frequency
F=1/T
Hz

PROCEDURE: -
1] Connections are made as shown in the circuit diagram
2] Adjust the CRO controls to obtain the wave form on CRO
3] Measure the time period T and find the frequency, f= 1 / T H 4] Measure & compare
this value with expected value
5] Repeat the experiment for different value of C


FULL-WAVE BRIDGE RECTIFIER

AIM:Set up a Full-Wave Bridge Rectifier with a capacitor filter and study its
performance.

APPARATUS:Transformer, Diode, Capacitor, Resistance Box, Rheostat, DC
Milliammeter, DC Voltmeter, AC Voltmeter, Plug key.

FORMULA:
Ripple Factor =

% Voltage Regulation =

Ripple Factor in absence of filter = r = 0.482

Efficiency of Rectifier = 81.2 %

THEORY:
Rectifier is a device that converts alternating current into unidirectional direct
current. A full-wave rectifier rectifies both the positive and negative half-cycles of
the input ac signal. A bridge rectifier utilizes 4 diodes connected as in the circuit
diagram to accomplish full wave rectification.
Operation of the circuit is like this During positive half cycle of input sine wave,
point A is positive w.r.t. point B. Diodes D1 and D2 are forward biased where as
diodes D3 and D4 are reverse biased.. Hence only diodes D1 & D3 conduct during
the positive half cycle while diodes D3 & D4 do not conduct current. If the filtering
condenser C is not in the circuit then always current through (both during +ve & -
ve half cycles of input current flows through input resistance) R & Rh (in circuit)
will flow in the same direction. But current flowing through load in the absence of
the filter is unidirectional and pulsating one, point D of the diode acts as the Anode
and point C acts as Cathode. Output of the rectifier being pulsating, contains DC
component as well as AC component. This type of output is not useful for driving
sophisticated electronic circuits. In fact, these circuits require steady DC output.
A circuit that converts pulsating output from rectifier into a steady DC level is
known as Filter, because it filters off or smoothens the output.

The filter used here is a Shunt Capacitor Filter. Here, capacitor of suitable value C1
is connected across the rectifier and is parallel to the load resistance R & Rh. This
type of filter is Capacitor Input Filter. It often allows impedance path for DC
portion of the output. The filtering action is shown in the output wave form. By
looking at it, one can see that even after filtering action, small amount of AC
remains unfiltered in the output. The remaining AC in DC component of the output
is called Ripple (unfiltered AC remains in outut). and is written a r = 1 / 4 .
This indicates that ripple factor depends on C and load resistance.

CIRCUIT DIAGRAM:

OBSERVATION:
Sl. No.
Load
Resistance
Vdc
(Volt)
Vac
(Volt)
Iac
(mA)
Ripple
Factor
Vac / Vdc
% Voltage
Regulation
1

2

3

4

5

6

7

8

9

10


PROCEDURE:
1) Connections are done as shown in the circuit diagram.
2) Keep the plug key (k) open, switch on the Ac mains note down Vdc and Vac.
3) The plug key is closed and the reading of I, Vac and Vdc are noted down for
corresponding readings.
4) With the increase of Rheostat it is varied for different readings of I, Vac are
noted.
5) After completion of taking the readings calculate the ripple factor using formula.

6) Calculate the percentage of regulator using the formula.

Where, V
NL
is the Voltmeter reading when no current is passed through it.

CALCULATIONS:


ZENER DIODE CHARACTERISTICS

AIM: - Set up electronic circuit to study the reverse current characteristics of
zenerdiode of power 0.5w and breakdown voltage 6.2v and hence determine.

1. Knee current I
2. Incremental zener resistance Rz
3. Range of Iz over which Vz remains constant

APPARATUS: - Transistor, power supply, Rheostat, current limiting resistor,
Zener diode, digital multimeter, to measure Vz, digital multimeter Iz.

THEORY: - Zener diode is reverse biased, heavily doped P.N diode that is operated
in the breakdown region, where current is limited by both external resistance and
power rating of the diode.
Zener diode at breakdown voltage VB breakdown due to zener effect and
avalanche effect usually at breakdown voltage one of the above two effects will
predominate depending upon breakdown potential difference.
In case of zener effect, breaking of the bond i.e covalent bond by strong
electric field occurs. Avalanche effect occurs due to at higher voltage, when
thermally generated electrons acquire enough to produce more carriers by collision.
Maximum current required to sustain breakdown is called knee current I
k

The maximum current which zener diode can withstand without getting overheated
or burnt is represented by I max. If the current is more than this maximum value,
zener diode will burn out due to overheating.
To reduce overheating, a limiting resistance Rs is connected in series with
zener diode.
Value of Rs is calculated as follows:
P = Power of zener diode = Vz Iz
:. Iz = P
Vz
Where, Vz = break down voltage of diode
Iz = Current
I max = Selected maximum current allowed to pass through zener diode = 50% of
Iz

Then Rs = Vin Vz
Imax
Where, Vin = applied voltage.
Reverse current character of zener diode is as shown in the nature of graph.
Diode passes some resistance called zener dynamic resistance Rz. Ideal
zener diode characteristic is not truly vertical, however the zener dynamic R is
very small. This means for considerable increase in Iz the value of Iz remains almost
same. Vz value of diode remain constant over range Ik I amx

CIRCUIT DIAGRAM:

NATURE OF GRAPH:

OBSERVATIONS:-
1. Voltage selected in TPS = Vin =
2. Zener diode break down voltage =
3. I amx
4. Limiting resistance =
5. Actual value of Rs, selected =

TABULAR COLUMN:
SI. NO. I
Z
in
mA
V
Z
(VOLTS)


CACULATIONS:

AB=

BC=

R
Z
=

Range of current = I
K
to I
max

Bca Experiments

Hochgeladen von

Dokumentinformationen

Originaltitel

Copyright

Verfügbare Formate

Dieses Dokument teilen

Dokument teilen oder einbetten

Freigabeoptionen

Stufen Sie dieses Dokument als nützlich ein?

Sind diese Inhalte unangemessen?

Copyright:

Verfügbare Formate

Bca Experiments

Hochgeladen von

Copyright:

Verfügbare Formate

EXPERIMENT NO: DATE:

Department of BCA and B.Sc(CS) ,KSCD.

Das könnte Ihnen auch gefallen