1

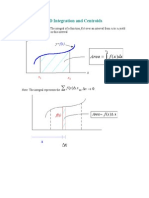
Chapter 2: Multiple Integrals

Definite integral ( )
b
a
f x dx
}
for function of one independent variable is used to
approximate the region in the plane, which is bounded by the continuous function
( ) 0 f x > , the x-axis, and the line x a = and x b = .



Similarly, the double integral for a function of two independent variables
( , )
R
f x y dA
}}
, in fact, approximates the volume of a solid under the surface
( , ) z f x y = and over region R.



It should be noted that:
Area of Region = 1
R
dA
}}

Volume = ( , )
R
f x y dA
}}


y
x
z
a
b
c
d
z =
f(x
,y)
R
Double Integral
2
Chapter 2: Multiple Integrals


Partial Definite Integrals
- The symbols ( , )
b
a
f x y dx
}
and ( , )
d
c
f x y dy
}
denote partial definite integrals.
- ( , )
b
a
f x y dx
}
is called partial definite integral with respect to x, which is
evaluated by holding y fixed and integrating with respect to x.
- ( , )
d
c
f x y dy
}
is called partial definite integral with respect to y, which is
evaluated by holding x fixed and integrating with respect to y.

Example 1
Calculate the value of
1
2
0
xy dx
}
and
1
2
0
xy dy
}
.
Solution
1
1 1
2 2 2 2 2 2 2
2 2
0 0 0
(1) (0)
2 2 2 2
x
x
y x y y y
xy dx y xdx
=
=
= = = =
} }



1
1 1 3 3 3
2 2
0 0 0
(1) (0)
3 3 3 3
y
y
xy x x x
xy dy x y dy
=
=
= = = =
} }





Method of Integration
If ( , ) f x y is function of two variables over a rectangular region
{( , ) | , } R x y a x b c x d = s s s s , then
( , ) ( , )
d b d b
c a c a
f x y dxdy f x y dx dy
(
=
(

} } } }

( , ) ( , )
b d b d
a c a c
f x y dydx f x y dy dx
(
=
(

} } } }

which are known as repeated/iterated integrals.


Double Integral over Rectangular Region
3
Chapter 2: Multiple Integrals

Example 2
Evaluate
2 1
2
0 0
xy dxdy
} }
and
1 2
2
0 0
xy dydx
} }
.

Solution
1
2 1 2
2 2
2
0 0 0 0
2
x
x
x y
xy dxdy dy
=
=
(
=
(

} } }

2
1 2 1 3
2
0 0 0 0
3
y
y
xy
xy dydx dx
=
=
(
=
(

} } }


2
2
0
2
2
0
2
3
0
3 3
0
2 2
2
6
2 0
6 6
4
3
y
y
y
dy
y
dy
y
=
=
| |
=
|
\ .
=
(
=
(

=
=
}
}

1
0
1
0
1
2
0
2 2
8 0
3 3
8
3
4
3
4(1) 4(0)
3 3
4
3
x
x
x
dx
x
dx
x
=
=
| |
=
|
\ .
=
(
=
(

=
=
}
}


It can be observed that these two iterated integrals have the same value. Generally, it is stated
in the theorem as follows:










Example 3
Evaluate the double integral (3 )
R
x y dA
}}
over rectangle {( , ) | 0 2, 0 1} R x y x x = s s s s .

Solution
2 1
0 0
(3 ) (3 )
R
x y dA x y dydx =
}} } }

Fubinis Theorem
Let R be the rectangle defined by the equalities a x b s s and c y d s s . If ( , ) f x y is
continuous on this rectangle, then
( , ) ( , ) ( , )
d b b d
R c a a c
f x y dA f x y dxdy f x y dydx = =
}} } } } }


4
Chapter 2: Multiple Integrals


1
2
2
0 0
2
2 2
0
2
0
2
2
0
2 2
3
2
(1) (0)
3(1) (1) 3(0) (0)
2 2
5
2
5
2 2
5(2) (2) 5(0) (0)
2 2 2 2
3
y
y
x
x
y
y xy dx
x x dx
x dx
x x
=
=
=
=
=
( (
=
( (

| |
=
|
\ .
=
| | | |
=
| |
\ . \ .
=
}
}
}





Example 4
Calculate the volume formed by the surface
2 2
8 z x y = over rectangle
{( , ) | 1 1, 1 1} R x y x x = s s s s .

Solution
1 1
2 2 2 2
1 1
(8 ) (8 )
R
x y dA x y dydx

=
}} } }


1
1 3
2
1 1
1 3 3
2 2
1
1
2
1
8
3
(1) ( 1)
8(1) (1) 8( 1) ( 1)
3 3
2
(16 2 )
3
y
y
y
y x y dx
x x dx
x dx
=
=

(
=
(

( (
=
( (

=
}
}
}

x
y
0 2
1
R
5
Chapter 2: Multiple Integrals


1
2
1
1
3
1
3 3
46
( 2 )
3
46 2
3 3
46 2(1) 46 2( 1)
(1) ( 1)
3 3 3 3
88
3
x
x
x dx
x
x

=
=
=
(
=
(

( (
=
( (

=
}











In applying double integrals over non-rectangular regions, one of the challenges is to
determine the intervals of the integrals.
Technique of using vertical stripe or horizontal stripe is applicable, where both
of them will give the same final answer.

Type 1 Region (Vertical Stripe)
Type 1 region contains points ( , ) x y such that for each fixed x between constants a and b,
y varies from
1
( ) g x to
2
( ) g x , where
1
( ) g x and
2
( ) g x are continuous functions.
Thus, the double integrals ( , )
R
f x y dA
}}
is given by:
2
1
( )
( )
( , ) ( , )
y g x b
R a y g x
f x y dA f x y dydx
=
=
=
}} } }




x
y
-1
1
1
R
-1
Double Integrals over Non-Rectangular Regions
) (
1
x g y =
) (
2
x g y =
a
b
R R
) (
1
x g y =
) (
2
x g y =
a
b
R R
6
Chapter 2: Multiple Integrals

Type 2 Region (Horizontal Stripe)
Type 2 region contains points ( , ) x y such that for each fixed y between constants c and d,
x varies from
1
( ) h y to
2
( ) h y , where
1
( ) h y and
2
( ) h y are continuous functions.
Thus, the double integrals ( , )
R
f x y dA
}}
is given by:
2
1
( )
( )
( , ) ( , )
x h y d
R c x h y
f x y dA f x y dxdy
=
=
=
}} } }



Example 5
Let R be the triangular region enclosed by the line 0 y = , 2 y x = and 1 x = . Evaluate the
double integral
( )
R
x y dA +
}}

using iterated integral with:
(a) y-integration first
(b) x- integration first
Solution
(a)
2 1
0 0
( ) ( )
y x
R y
x y dA x y dydx
=
=
+ = +
}} } }


2
1 2
0 0
1 2 2
0
1
2
0
1
3
0
2
(2 ) (0)
(2 ) (0)
2 2
4
4
3
4
3
y x
y
y
xy dx
x
x x x dx
x dx
x
=
=
= +
( (
= + +
( (

=
=
=
}
}
}

7
Chapter 2: Multiple Integrals

(b)
2 1
0 / 2
( ) ( )
x
R x y
x y dA x y dxdy
=
=
+ = +
}} } }


1
2 2
0 / 2
2 2 2
0
2 2
0
2
2 3
0
2
1 ( / 2)
(1) ( )
2 2 2
1 5
2 8
5
2 2 24
5
1 2 0
3
4
3
x
x y
x
yx dy
y y
y y dy
y
y dy
y y y
=
=
= +
( (
= + +
( (

= +
= +
(
= +
(

=
}
}
}

Example 6
By using double integrals, find the area of the regions enclosed by
2
4 y x = and 3 . y x =

Solution






To find the intercepting points between
2
4 y x = and 3 y x = , we let
2
2
4 3
3 4 0
( 4)( 1) 0
x x
x x
x x
=
+ =
+ =

x = -4 and x = 1

When x = -4, y = 3x = 3(-4) = -12
When x = 1, y = 3x = 3(1) = 3
-5 -4 -3 -2 -1 0 1 2 3 4 5
-25
-20
-15
-10
-5
0
5
10
15
(1,3)
(-4,-12)
R
8
Chapter 2: Multiple Integrals

Area of region, R =
2
4 1
4 3
1
y x
y x
dydx
=
=
} }


2
4
1
4 3
1
2
4
1
3 2
4
(4 3 )
3
4
3 2
1 3 ( 64)
4(1) 16 (24)
3 2 3
20.83
x
x
y dx
x x dx
x x
x

=
=
=
( (
=
( (

=
}
}


Example 7
By using double integrals, find the volume of the solid enclosed by the planes
2 3 6, 0, 0 x y z x y + + = = = and 0 z = .
Solution
Volume = ( , )
R
f x y dA
}}


6 2
3 3
0 0
6 2
3 2
3
0 0
2
3 2
0
3
2
0
3
3
0
(6 2 3 )
3
(6 2 )
2
(6 2 ) 3 6 2
3 2 3
1
(6 2 )
6
1 (6 2 )
6 6
1
(0 ( 36))
6
6
x
y
x
x y
x
x
x
x
x
x
x
x y dydx
y
x y dx
x x
dx
x dx
x

=
=
= =

=
=
=
=
=
=
=
(
=
(

| |
=
|
\ .
=
(
=
(

=
=
} }
}
}
}


y
2
2x+3y=6
R
3 x
9
Chapter 2: Multiple Integrals

Example 8
By using double integrals, evaluate ( )
R
x y dA +
}}
, where R is the region bounded by y x =
and
2
y x = .
Solution
2
1
0
( ) ( )
y x x
R x y x
x y dA x y dydx
= =
= =
+ = +
}} } }


2
1 2
0
1 4
3/ 2 3
0
1
2 4 5
5/ 2
0
2
2 2
2
5 4 4 10
3
10
x
x
x x
x
x
y
xy
x x
x x dx
x x x
x
=
=
=
=
(
= +
(

= +
(
= +
(

=
}
}

Example 9
Given that
4 2
3
0 x
y dydx
} }
. Interchange the order of integration and evaluate
Solution
From
4 2
3
0 x
y dydx
} }
, we derive the information as shown in the figure as follows, where the
technique of vertical stripe has been used.
Thus, interchange the order of integration from dydx to dxdy, we have:
2
2
2 2
3 3
0
0 0 0
x y
x y
x
x
y dxdy y x dy
=
=
=
=
=
} } }


2
5
0
32
3
y dy =
=
}

0 0.2 0.4 0.6 0.8 1 1.2 1.4
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 0.5 1 1.5 2 2.5 3 3.5 4
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2