INNOVA J UNIOR COLLEGE

J C 2 PRELIMINARY EXAMINATION 2
in preparation for General Certificate of Education Advanced Level
Higher 2


CANDIDATE
NAME

CLASS INDEX NUMBER


MATHEMATICS
Paper 1



Additional Materials: Answer Paper
Graph Paper
List of Formulae (MF15)

9740/01

15 September 2010

3 hours


READ THESE INSTRUCTIONS FIRST

Do not open this booklet until you are told to do so.

Write your name, class and index number on all the work you hand in.

Write in dark blue or black pen on both sides of the paper. You may use a soft pencil for any
diagrams or graphs.
Do not use staples, paper clips, highlighters, glue or correction fluid.

Answer all the questions.
Give non-exact numerical answers correct to 3 significant figures, or 1 decimal place in the
case of angles in degrees, unless a different level of accuracy is specified in the question.
You are expected to use a graphic calculator.
Unsupported answers from a graphic calculator are allowed unless a question specifically
states otherwise.
Where unsupported answers from a graphic calculator are not allowed in a question, you
are required to present the mathematical steps using mathematical notations and not
calculator commands.

You are reminded of the need for clear presentation in your answers.

At the end of the examination, fasten all your work securely together.

The number of marks is given in brackets [ ] at the end of each question or part question.



This document consists of 6 printed pages.

Innova J unior College [Turn over

IJ C/2010/J C2 9740/01/S/10

2

1 For any given mass of gas, the volume V cm
3
and pressure p (in suitable units) satisfy
the relationship

1
n
V p
k
= ,
where k and n are constants.
For a particular type of gas, 2.3 n = . At an instant when volume is 32 cm
3
, the
pressure is 105 units and the pressure is increasing at a rate of 0.2 units s
1
.
Calculate the rate of decrease of volume at this instant. [4]


2 Given that the coefficient of
2
x in the series expansion of
( )
2
1 3
n
x +
is 108, find the
value of n, where n is a positive integer. [4]



3 The sequence of numbers
n
u , where 1, 2, 3,..., n = is such that

1
9
8
u = and
1
8 7 8
n n
u u n
+
= + + .
Use the method of mathematical induction to show that

3
2
n
n
u n

= + for 1 n > . [5]
(i) Determine if the sequence converges. [1]
(ii) Find
1
n
r
r
u
=

in terms of n. [2]


IJ C/2010/J C2 9740/01/S/10 [Turn over

3
4













The diagram shows a quadrilateral OABC with OA AB = and OC BC = .
Points A and B have position vectors
1
2
o
| |
|
|
|
\ .
and
1
0
1
| |
|
|
|
\ .
respectively.
(a) Find cosine of angle OAB in terms of o . [2]
(b) M is the midpoint of OB and 4AM MC =

. By considering the area of the
quadrilateral OABC, show that

5
2
OA OC OA OB =

. [4]


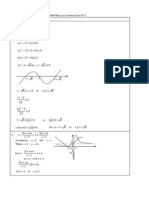
5 Illustrate, on a single Argand diagram, the locus of the point representing the complex
number z that satisfies both the inequalities
( )
3
arg 3 3i
4 2
z
t t
< s and 3 3i 2 z s . [4]
(i) Find the greatest and least values of 3i z + . [2]
(ii) Find the least possible value of ( ) z arg , giving your answer in radians. [3]

C
B
O
A
M

IJ C/2010/J C2 9740/01/S/10

4
6 Show, by means of the substitution
2
w x y = , that the differential equation
d
d
2 3 0
y
x
x y xy + + =
can be reduced to the form

d
d
3
w
x
w = . [2]
Hence find y in terms of x, given that
1
2
y = when 2 x = . [4]

7 A curve is defined parametrically by
2cos x t = , 2 1 y t = ,
where 0 t t < s .
(i) Find the equation of the normal to the curve at the point P where
3
t
t
= . [5]
(ii) The normal at P meets the y-axis at N and the x-axis at M. Given that the curve
meets the y-axis at Q, find the area of triangle MNQ, correct to 1 decimal place.
[5]

8 A curve has equation
2 2
( 4)
1
4 9
x y
= .
(i) Sketch the curve, stating the equations of the asymptotes and the coordinates
of the vertices. [3]
(ii) The region enclosed by the curve
2 2
( 4)
1
4 9
x y
= , the x-axis and the line
2 x = is rotated through 4 right angles about the y-axis to form a solid of
revolution of volume V. Find the exact value of V, giving your answer in terms
of t . [4]



IJ C/2010/J C2 9740/01/S/10 [Turn over

5
9 In a medical research centre, a particular species of insect is grown for treatment of
open wounds. The insects are grown in a dry and cool container, and they are left to
multiply. The increase in the number of insects at the end of each week is at a
constant rate of 4% of the number at the beginning of that week. At the end of each
week, 10 of the insects would die due to space constraint and are removed from the
container.
A researcher puts y insects at the beginning of the first week and then a further y at the
beginning of the second and each subsequent week. He also decides that he will not
take any live insects out of the container.
(i) How many insects will there be in the container at the end of the first week?
Leave your answer in terms of y. [1]
(ii) Show that, at the end of n weeks, the total number of insects in the container is
( ) ( ) 26 250 1.04 1
n
y
(


. [4]
(iii) Find the minimum number of complete weeks for the population of the insects
to exceed 125 13 y . [4]

10 The functions f and g are defined as
f : 1 x x for 1 x s
g: e 1
x
x

for 0 x >
(i) Define
1
f

in a similar form, including its domain. [3]

(ii) State the relationship between f and
1
f

, and sketch the graphs of f and

1
f

on
the same diagram. [3]
(iii) Find the exact solutions of the equation

1
f ( ) f ( ) x x

= . [2]
(iv) Show that the composite function fg exists. [2]
(v) Given that h( ) fg( ) x x ' = for 0 x > , show that h is an increasing function for
0 x > . [2]





IJ C/2010/J C2 9740/01/S/10

6
11 (a) Write 2cos3 cos x x in the form ( ) ( ) cos cos px qx + , where p and q are
positive integers. [1]
Hence find
(i) cos3 cos d x x x
}
, [2]
(ii) the exact value of
4
0
cos3 cos d x x x x
}
t
. [4]
(b) State a sequence of transformations which transform the graph of sin y x = to
the graph of
3
sin 2
2
y x t
| |
=
|
\ .
. [2]
(c) Find the numerical value of the area of the region bounded by the curves
cos3 cos y x x = and
3
sin 2
2
y x t
| |
=
|
\ .
for 0
2
x
t
s s . [3]

12 A plane
1
t has equation
2
1 9
3
| |
|
=
|
|
\ .
r. and a line
1
has equation
3 4
0 1
0 2
| | | |
| |
= +
| |
| |

\ . \ .
r .

(i) Find the coordinates of P, the point of intersection of
1
and
1
t . [4]
Hence, or otherwise, find the shortest distance from point A (3, 0, 0) to
1
t .
[2]
The equations of planes
2
t and
3
t are given as

2
t :
1 2 2
1 0 2
1 3 1
s t
| | | | | |
| | |
= + +
| | |
| | |

\ . \ . \ .
r , and

3
t : x y z o | + = , where , o | e.
(ii) Find the equation of plane
2
t in the form d r n = . Explain why the planes
1
t and
2
t intersect. [4]
(iii) The line of intersection of planes
1
t and
2
t is
2
. The line
2
has equation

3 2
3 1
2 1
| | | |
| |
+
| |
| |

\ . \ .
r = .
Given that the three planes
1
t ,
2
t and
3
t do not have any points in common,
find the conditions satisfied by o and | . [3]