11.

6 FUGACITY AND FUGACITY COEFFICIENT:

SPECIES IN SOLUTION
The definition of the fugacity of a species in solution is parallel to the definition of the purespecies
fugacity. For species i in a mixture of real gases or in a solution of liquids, the equation
analogous to Eq. (1 1.28), the ideal-gas expression, is:
pi -- ri (T) + RT In ti (1 1.42)
where fi is the fugacity of species i in solution, replacing the partial pressure yi P. This
definition of ti does not make it a partial molar property, and it is therefore identified by a
circumflex rather than by an overbar.
A direct application of this definition indicates its potential utility. Equation 11.6 is the
fundamental criterion for phase equilibrium. Since all phases in equilibrium are at the same
temperature, an alternative and equally general criterion follows immediately from Eq. (1 1.42):
Thus, multiple phases at the same T and P are in equilibrium when
the fugacity of each constituent species is the same in all phases.
This criterion of equilibrium is the one usually applied by chemical engineers in the solution
of phase-equilibrium problems.
For the specific case of multicomponent vaporlliquid equilibrium, Eq. (1 1.43) becomes:
Equation (1 1.38) results as a special case when this relation is applied to the vaporAiquid
equilibrium of pure species i .
The definition of a residual property is given in Sec. 6.2:
MR - M - I,@ (6.41)
where M is the molar (or unit-mass) value of a thermodynamic property and M'g is the value
that the property would have for an ideal gas of the same composition at the same T and P. The
defining equation for apartial residual property M: follows from this equation. Multiplied by
n mol of mixture, it becomes:
Differentiation with respect to ni at constant T, P, and nj gives:
Reference to Eq. (1 1.7) shows that each term has the form of a partial molar property.
Thus, Since residual properties measure departure from ideal-gas values, their most logical use is as
gas-phase properties, but in fact they also find use as liquid-phase properties.
Written for the residual Gibbs energy, Eq. (1 1.45) becomes:
an equation which defines the partial residual Gibbs energy.
Subtracting Eq. (1 1.28) from Eq. (1 1.42), both written for the same T and P, yields:
This result combined with Eq. (1 1.46) and the identity pi E Ci gives:
where by definition
The dimensionless ratio $i is called the fugacity coefJicient of species i in solution. Although
most commonly applied to gases, the fugacity coefficient may also be used for liquids, and in
this case mole fraction yi is replaced by xi.
Equation (1 1.47) is the analog of Eq. (1 1.31), which relates $i to G;. For an ideal gas,
G: is necessarily zero; therefore $jg = 1, and
Thus the fugacity of species i in an ideal-gas mixture is equal to its partial pressure.
The Fundamental Residual-Property Relation
In order to extend the fundamental property relation to residual properties, we transform
Eq. (1 1.2) into an alternative form through the mathematical identity (also used in Sec. 6.1):
1 nG
d (1-;) - --d(nG)- -dT Ri" RT2
In this equation d(nG) is eliminated by Eq. (1 1.2) and G is replaced by its definition, H - TS.
The result, after algebraic reduction, is:
All terms in Eq. (1 1.50) have the units of moles; moreover, in contrast to Eq. (1 1.2), the
enthalpy rather than the entropy appears on the right side.
Equation (1 1.50) is a general relation expressing nGIRT as a function of all of its canonical variables, T, P, and the
mole numbers. It
reduces to Eq. (6.37) for the special case of 1 mol of a constant-composition phase. Equations
(6.38) and (6.39) follow from either equation, and equations for the other thermodynamic
properties then come from appropriate defining equations. Knowledge of GIRT as a function
of its canonical variables allows evaluation of all other thermodynamic properties, and therefore
implicitly contains complete property information. However, we cannot directly exploit this
characteristic, and for this reason develop an analogous equation relating residual properties.
Since Eq. (1 1 SO) is general, it may be written for the special case of an ideal gas:
In view of Eqs. (6.41) and (1 1.46), subtracting this equation from Eq. (1 1.50) gives:
Equation (1 1.51) is thefundamental residual-property relation. Its derivation from Eq. (1 1.2)
parallels the derivation in Chap. 6 that led from Eq. (6.10) to Eq. (6.42). Indeed, Eqs. (6.10) and
(6.42) are special cases of Eqs. (1 1.2) and (1 1.51), valid for 1 mol of a constant-composition
fluid. An alternative form of Eq. (1 1.51) follows by introduction of the fugacity coefficient as
given by Eq. (1 1.47):
Equations so general as Eqs. (1 1.51) and (1 1.52) are useful for practical application only
in their restricted forms. Division of Eqs. (1 1.5 1) and (1 1.52) by d P and restriction to constant
T and composition leads to:
Similarly, division by dT and restriction to constant P and composition gives:
These equations are restatements of Eqs. (6.43) and (6.44) wherein the restriction of the derivatives
to constant composition is shown explicitly. They lead to Eqs. (6.46), (6.47), and (6.48)
for the calculation of residual properties from volumetric data. Moreover, Eq. (1 1.53) is the
basis for the direct derivation of Eq. (1 1.34), which yields fugacity coefficients from volumetric
data. It is through the residual properties that this kind of experimental information enters into
the practical application of thermodynamics. In addition, from Eq. (1 1.52),
This equation demonstrates that In ai is a partial property with respect to G R / ~
Fugacity Coefficients from the Virial Equation of State
Values of )i for species i in solution are readily found from equations of state. The simplest
form of the virial equation provides a useful example. Written for a gas mixture it is exactly
the same as for a pure species: The mixture second virial coefficient B is a function of temperature and composition.
Its exact
composition dependence is given by statistical mechanics, and this makes the virial equation
preeminent among equations of state where it is applicable, i.e., to gases at low to moderate
pressures. The equation giving this composition dependence is:
where y represents mole fractions in a gas mixture. The indices i and j identify species,
and both run over all species present in the mixture. The virial coefficient Bij characterizes
a bimolecular interaction between molecule i and molecule j , and therefore Bij = Bji. The
summations account for all possible bimolecular interactions.
For a binary mixture i = l , 2 and j = l,2; the expansion of Eq. (1 1.57) then gives:
Two types of virial coefficients have appeared: Bll and B22, for which the successive subscripts
are the same, and BI2, for which the two subscripts are different. The first type is a purespecies
virial coefficient; the second is a mixture property, known as a cross coeficient. Both
are functions of temperature only. Expressions such as Eqs. (1 1.57) and (1 1.58) relate mixture
coefficients to pure-species and cross coefficients. They are called mixing rules.
Equation (1 1.58) allows derivation of expressions for In $1 and In $2 for a binary gas
mixture that obeys Eq. (3.37). Written for n mol of gas mixture, it becomes:
Differentiation with respect to nl gives:
Substitution for in Eq. (1 1.56) yields:
where the integration is elementary, because B is not a function of pressure. All that remains
is evaluation of the derivative.
Equation (1 1.58) for the second virial coefficient may be written:
where 812 -- 2B12 - Bll - B22
Since yi = ni/n,
n B = ~ ~ B+ In2BI 22 + -1a21l122 2 n
Differentiation gives:
A P
Therefore, In41 = -R(&TI + ~22812) ( 11 .59)
. P
Similarly, In42 = -R(BT2 2 + yf612)
(1 1.60)
Equations (1 1.59) and ( 1 1.60) are readily extended for application to multicomponent gas
mixtures; the general equation is:9
where the dummy indices i and j run over all species, and
Sik -- 2Bik - Bii - Bkk &' J . -= 2 B'.J . - B .1.1- B . .J J
with Sii = 0, 8kk = 0, etc., and Ski = aik, etc.
11.7 GENERALIZED CORRELATIONS FOR THE
FUGACITY COEFFICIENT
The generalized methods developed in Sec. 3.6 for the compressibility factor Z and in Sec. 6.7
for the residual enthalpy and entropy of pure gases are applied here to the fugacity coefficient.
Equation (1 1.34) is put into generalized form by substitution of the relations,
pr
Hence, d P,
ln4i = (z' - 1)- (1 1.62)
P,
where integration is at constant T,. Substitution for Zi by Eq. (3.54) yields:
where for simplicity we have dropped subscript i. This equation may be written in alternative
form:
In4 = ln@O + w ln4' (1 1.63)
p,
where 1 n 4O- - l (Z, , -1)- dP, and l n d =
p,
The integrals in these equations may be evaluated numerically or graphically for various values
of T, and P, from the data for Z0 and Z' given in Tables E.l through E.4 (App. E).
Another method, and the one adopted by Lee and Kesler to extend their correlation to fugacity
coefficients, is based on an equation of state.
Since Eq. (1 1.63) may also be written,
4 = (4O)(4'>" (1 1.64)
we have the option of providing correlations for 4' and 4' rather than for their logarithms.
This is the choice made here, and Tables E. 13 through E. 16 present values for these quantities
as derived from the LeeIKesler correlation as functions of T, and P,, thus providing a threeparameter
generalized correlation for fugacity coefficients. Tables E. 13 and E. 15 for #' can be
used alone as a two-parameter correlation which does not incorporate the refinement introduced
by the acentric factor.
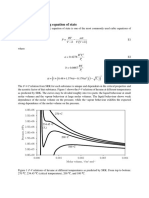
A useful generalized correlation for In # results when the simplest form of the virial
equation is valid. Equations (3.58) and (3.59) combine to give:
Substitution in Eq. (1 1.62) and integration yield:
This equation, used in conjunction with Eqs. (3.61) and (3.62), provides reliable values of 4
for any nonpolar or slightly polar gas when applied at conditions where
Named functions, HRB(TR,PR,OMEGA) and SRB(TR,PR,OMEGA), for evaluation
of H R/ RT, and S R/ R by the generalized virial-coefficient correlation were described in
Sec. 6.7. Similarly, we introduce here a function named PHIB(TR,PR,OMEGA) for evaluation
of 4:
It combines Eq. (1 1.65) with Eqs. (3.61) and (3.62), as indicated in the representative computer
programs given in App. D. For example, the value of 4 for 1-butene vapor at the conditions of
Example 6.8, Step (b), is:
The generalized correlation just described is for pure gases only. The remainder of this
section shows how the virial equation may be generalized to allow calculation of fugacity
coefficients Ji for species in gas mixtures.
The general expression for calculation of In Jk from second-virial-coefficient data is given
by Eq. (1 1.61). Values of the pure-species virial coefficients Bkk, Bii, etc., are found from the
generalized correlation represented by Eqs. (3.59), (3.61), and (3.62). The cross coefficients
Bik, Bij, etc., are found from an extension of the same correlation. For this purpose, Eq. (3.59)
is rewritten in the more general form: lo
where BO and B' are the same functions of Tr as given by Eqs. (3.61) and (3.62). The combining
rules proposed by Prausnitz for calculation of wij, Tcij,a nd PCija re:
In Eq. (1 1.68), kij is an empirical interaction parameter specific to an i- j molecular pair.
When i = j and for chemically similar species, kij = 0. Otherwise, it is a small positive
number evaluated from minimal P VT data or in the absence of data set equal to zero.
When i = j, all equations reduce to the appropriate values for a pure species. When
i # j, these equations define a set of interaction parameters having no physical significance.
Reduced temperature is given for each i j pair by TTi-j-= T/T cij.
For a mixture, values of Bij from Eq. (1 1.66) substituted into Eq. (1 1.57) yield the
mixture second virial coefficient B, and substituted into Eq. (1 1.61) [Eqs. (1 1.59) and (1 1.60)
for a binary] they yield values of In $i.
The primary virtue of the generalized correlation for second virial coefficients presented
here is simplicity; more accurate, but more complex, correlations appear in the literature."