Beruflich Dokumente
Kultur Dokumente
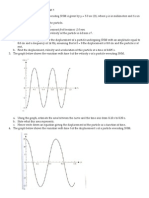
Physics I Problems PDF
Hochgeladen von
BOSS BOSSOriginalbeschreibung:
Originaltitel
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Physics I Problems PDF
Hochgeladen von
BOSS BOSSCopyright:
Verfügbare Formate
470
CHAPTER 14 Periodic Motion
between the tabletop and the spheres for the spheres to roll without
slipping as they move back and forth on the end of the spring. Show
that the motion of the center of mass of the spheres is simple harmonic and calculate the period.
14.95 . CP In Fig. P14.95 the Figure P14.95
upper ball is released from rest,
collides with the stationary lower
ball, and sticks to it. The strings
are both 50.0 cm long. The upper
ball has mass 2.00 kg, and it is initially 10.0 cm higher than the
lower ball, which has mass
3.00 kg. Find the frequency and
maximum angular displacement
10.0 cm
of the motion after the collision.
14.96 .. CP BIO T. rex. Model
the leg of the T. rex in Example
14.10 (Section 14.6) as two uniform rods, each 1.55 m long,
joined rigidly end to end. Let the lower rod have mass M and the
upper rod mass 2M. The composite object is pivoted about the top
of the upper rod. Compute the oscillation period of this object for
small-amplitude oscillations. Compare your result to that of
Example 14.10.
14.97 .. CALC A slender, uni- Figure P14.97
form, metal rod with mass M
is pivoted without friction about
an axis through its midpoint and
perpendicular to the rod. A horizontal spring with force constant
k is attached to the lower end of
the rod, with the other end of the
spring attached to a rigid supu
port. If the rod is displaced by a
small angle from the vertical
(Fig. P14.97) and released, show
that it moves in angular SHM
and calculate the period. (Hint: Assume that the angle is small
enough for the approximations sin L and cos L 1 to be
valid. The motion is simple harmonic if d 2u>dt 2 = - v2u, and the
period is then T = 2p>v.)
14.98 .. The Silently Ringing Bell Problem. A large bell is
hung from a wooden beam so it can swing back and forth with negligible friction. The center of mass of the bell is 0.60 m below the
pivot, the bell has mass 34.0 kg, and the moment of inertia of the
bell about an axis at the pivot is 18.0 kg # m2. The clapper is a
small, 1.8-kg mass attached to one end of a slender rod that has
length L and negligible mass. The other end of the rod is attached to
the inside of the bell so it can swing freely about the same axis as
the bell. What should be the length L of the clapper rod for the bell
to ring silentlythat is, for the period of oscillation for the bell to
equal that for the clapper?
14.99 ... Two identical thin Figure P14.99
rods, each with mass m and
length L, are joined at right
angles to form an L-shaped
L
L
object. This object is balanced
on top of a sharp edge (Fig.
P14.99). If the L-shaped object
is deected slightly, it oscillates.
Find the frequency of oscillation.
14.100 . CP CALC A uniform rod of length L oscillates through
small angles about a point a distance x from its center. (a) Prove
that its angular frequency is 2gx>31L2>122 + x 24. (b) Show that
its maximum angular frequency occurs when x = L> 112.
(c) What is the length of the rod if the maximum angular frequency
is 2p rad>s?
CHALLENGE PROBLEMS
14.101 ... The Effective Force
Figure P14.101
Constant of Two Springs.
(a)
Two springs with the same
unstretched length but different
k1
m
force constants k 1 and k 2 are
attached to a block with mass m
k2
on a level, frictionless surface.
Calculate the effective force
(b)
constant k eff in each of the three
cases (a), (b), and (c) depicted in
m
k1
k2
Fig. P14.101. (The effective force
constant is dened by gFx =
-k effx.) (d) An object with mass
m, suspended from a uniform
(c)
spring with a force constant k,
vibrates with a frequency 1.
m
k1
k2
When the spring is cut in half
and the same object is suspended from one of the halves,
the frequency is 2. What is the
ratio 2>1?
14.102 ... Two springs, each with unstretched length 0.200 m but
with different force constants k 1 and k 2, are attached to opposite
ends of a block with mass m on a level, frictionless surface. The
outer ends of the springs are now attached to two pins P1 and P2,
0.100 m from the original positions of the ends of the springs (Fig.
P14.102). Let k 1 = 2.00 N>m, k 2 = 6.00 N>m, and m =
0.100 kg. (a) Find the length of each spring when the block is in its
new equilibrium position after the springs have been attached to
the pins. (b) Find the period of vibration of the block if it is slightly
displaced from its new equilibrium position and released.
Figure P14.102
0.100 m 0.200 m
P1
0.200 m 0.100 m
P2
14.103 ... CALC A Spring with Mass. The preceding problems in this chapter have assumed that the springs had negligible
mass. But of course no spring is completely massless. To nd the
effect of the springs mass, consider a spring with mass M, equilibrium length L 0, and spring constant k. When stretched or compressed
to a length L, the potential energy is 12 kx 2, where x = L - L 0.
(a) Consider a spring, as described above, that has one end xed
and the other end moving with speed v. Assume that the speed of
points along the length of the spring varies linearly with distance l
from the xed end. Assume also that the mass M of the spring is
distributed uniformly along the length of the spring. Calculate the
kinetic energy of the spring in terms of M and v. (Hint: Divide the
spring into pieces of length dl; nd the speed of each piece in
Das könnte Ihnen auch gefallen
- Physics I Problems PDFDokument1 SeitePhysics I Problems PDFBOSS BOSSNoch keine Bewertungen
- O level Physics Questions And Answer Practice Papers 2Von EverandO level Physics Questions And Answer Practice Papers 2Bewertung: 5 von 5 Sternen5/5 (1)
- Ejercicios Desarrollado ONDASDokument5 SeitenEjercicios Desarrollado ONDASMariangelica Preciado NunezNoch keine Bewertungen
- Sheets PDFDokument6 SeitenSheets PDFmayank singhNoch keine Bewertungen
- Physics I Problems PDFDokument1 SeitePhysics I Problems PDFBOSS BOSSNoch keine Bewertungen
- Soal Untuk Ujian Materi Getaran-ADokument2 SeitenSoal Untuk Ujian Materi Getaran-ADella KhoirunnisaNoch keine Bewertungen
- Simple Harmonic MotionDokument7 SeitenSimple Harmonic MotionRaju SinghNoch keine Bewertungen
- Simple Harmonic MotionDokument7 SeitenSimple Harmonic MotionRaju SinghNoch keine Bewertungen
- SHM SubjectiveDokument8 SeitenSHM SubjectiveAtulNoch keine Bewertungen
- Lab # 5 and 6: Simple Harmonic OscillatorDokument6 SeitenLab # 5 and 6: Simple Harmonic OscillatorVictor CoronelNoch keine Bewertungen
- Physics Problems WavesDokument3 SeitenPhysics Problems WavesMalletNjonkemNoch keine Bewertungen
- Old-Exam.Questions-Ch-15 (Dr. Gondal, Phys101) : θ 0.08cos 4.43 tDokument3 SeitenOld-Exam.Questions-Ch-15 (Dr. Gondal, Phys101) : θ 0.08cos 4.43 tmukesh3021Noch keine Bewertungen
- 11 Physics Sample Papers Solved 05Dokument24 Seiten11 Physics Sample Papers Solved 05Shivam GargNoch keine Bewertungen
- Question 41Dokument7 SeitenQuestion 41Skye JabaNoch keine Bewertungen
- Taller 2Dokument2 SeitenTaller 2marcela galindoNoch keine Bewertungen
- Vibrations HW CH 1-4Dokument33 SeitenVibrations HW CH 1-4osullivryan67% (3)
- SHM Ex1Dokument2 SeitenSHM Ex1Kshitij BansalNoch keine Bewertungen
- Fisdas1 Tugas 3 FixDokument9 SeitenFisdas1 Tugas 3 FixNopran KurniawanNoch keine Bewertungen
- SOALDokument6 SeitenSOALFebryn NgkNoch keine Bewertungen
- Physics I Problems PDFDokument1 SeitePhysics I Problems PDFBOSS BOSSNoch keine Bewertungen
- Simple Harmonic MotionDokument7 SeitenSimple Harmonic Motionbishu_iitNoch keine Bewertungen
- Kelm 105Dokument6 SeitenKelm 105ASHISH KUMARNoch keine Bewertungen
- Types of PendulumDokument5 SeitenTypes of PendulumExpertsmindEdu100% (2)
- PCS125 Tutorial QuestionsDokument52 SeitenPCS125 Tutorial Questionsfurbac321Noch keine Bewertungen
- CBSE Class 11 Physics Sample Paper-09 (Solved)Dokument23 SeitenCBSE Class 11 Physics Sample Paper-09 (Solved)cbsesamplepaper0% (1)
- Bansal Simple Harmonic MotionDokument24 SeitenBansal Simple Harmonic Motionbhnprtp90Noch keine Bewertungen
- Chapter 15 Electric FieldsDokument17 SeitenChapter 15 Electric FieldsdrewNoch keine Bewertungen
- A2 RevisionDokument10 SeitenA2 Revisiongaya8404Noch keine Bewertungen
- Topic C: Energy - Examples SPRING 2014: V V V V e 0.0 e 0.5 e 1.0Dokument9 SeitenTopic C: Energy - Examples SPRING 2014: V V V V e 0.0 e 0.5 e 1.0ettypasewangNoch keine Bewertungen
- Latihan UTSDokument13 SeitenLatihan UTSAyu Patresia NababanNoch keine Bewertungen
- Simple Harmonic MotionDokument45 SeitenSimple Harmonic MotionKarrthiNoch keine Bewertungen
- Problems For Chapter 9Dokument13 SeitenProblems For Chapter 9LeJohn HsuNoch keine Bewertungen
- Phys124s10 hw02Dokument5 SeitenPhys124s10 hw02snyderbl2100% (1)
- II IIT IRP Physics Worksheet - 14 - SHMDokument6 SeitenII IIT IRP Physics Worksheet - 14 - SHMAshwin KumarNoch keine Bewertungen
- PHY 101 Chapter 10 PostDokument33 SeitenPHY 101 Chapter 10 PostkjneroNoch keine Bewertungen
- Assignment01Dokument3 SeitenAssignment01karthikNoch keine Bewertungen
- Sound and Wave ErxerciseDokument21 SeitenSound and Wave Erxercisepaulus1stNoch keine Bewertungen
- Chapter 10Dokument11 SeitenChapter 10kiaunaNoch keine Bewertungen
- Wiley Part2Dokument9 SeitenWiley Part2Andrian Dean Handika CsTahtaNoch keine Bewertungen
- Assigment 1Dokument2 SeitenAssigment 1Pankhuri Kumari0% (1)
- 4 - Oscillation and WavesDokument11 Seiten4 - Oscillation and WavesakhilNoch keine Bewertungen
- F - (Volume × Density × G)Dokument11 SeitenF - (Volume × Density × G)Gaurav ShekharNoch keine Bewertungen
- A Level PhysicsDokument6 SeitenA Level PhysicsPratibha BaluniNoch keine Bewertungen
- Oscillatory MotionDokument182 SeitenOscillatory MotionAlain McVaneyNoch keine Bewertungen
- Torque Dynamics ProblemsDokument3 SeitenTorque Dynamics ProblemsJoshua JonesNoch keine Bewertungen
- Chapter 8Dokument44 SeitenChapter 8Mohan ManickamNoch keine Bewertungen
- Phy Lab PDFDokument67 SeitenPhy Lab PDFAbhayNoch keine Bewertungen
- Chapter - 8 - Simple Harmonic MotionDokument12 SeitenChapter - 8 - Simple Harmonic MotionMohammed Aftab Ahmed0% (1)
- Simple Harmonic Motion IntroDokument37 SeitenSimple Harmonic Motion IntroChristine LobbNoch keine Bewertungen
- Simple Harmonic Motion: AP Physics BDokument19 SeitenSimple Harmonic Motion: AP Physics BMaureen GalinganNoch keine Bewertungen
- Simple Harmonic MotionDokument39 SeitenSimple Harmonic MotionJenievie EspinoNoch keine Bewertungen
- Rigid BodiesDokument8 SeitenRigid BodiesQuim SimonNoch keine Bewertungen
- Rotational ProblemDokument10 SeitenRotational Problemursml12Noch keine Bewertungen
- 11 Rotation and TorqueDokument94 Seiten11 Rotation and TorquePutri S100% (1)
- Taller 1Dokument4 SeitenTaller 1manuelNoch keine Bewertungen
- SHM - Wave - Sound Practice KeyDokument19 SeitenSHM - Wave - Sound Practice KeyanirudhNoch keine Bewertungen
- Practice Hookes and SHM SolutionsDokument10 SeitenPractice Hookes and SHM SolutionsZhong Huang100% (1)
- SHM and Waves Problem SetDokument5 SeitenSHM and Waves Problem SetbananacrunchNoch keine Bewertungen
- CBSE Class 1 English Worksheet PDFDokument1 SeiteCBSE Class 1 English Worksheet PDFManoj GuptaNoch keine Bewertungen
- CBSE Class 1 English Worksheet PDFDokument1 SeiteCBSE Class 1 English Worksheet PDFManoj GuptaNoch keine Bewertungen
- CBSE Class 1 English WorksheetsDokument1 SeiteCBSE Class 1 English WorksheetsBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetDokument2 SeitenCBSE Class 1 English WorksheetBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetDokument2 SeitenCBSE Class 1 English WorksheetBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetDokument1 SeiteCBSE Class 1 English WorksheetBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetDokument1 SeiteCBSE Class 1 English WorksheetBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetsDokument1 SeiteCBSE Class 1 English WorksheetsBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetDokument1 SeiteCBSE Class 1 English WorksheetBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetDokument1 SeiteCBSE Class 1 English WorksheetBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetDokument1 SeiteCBSE Class 1 English WorksheetBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetsDokument1 SeiteCBSE Class 1 English WorksheetsBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English WorksheetDokument1 SeiteCBSE Class 1 English WorksheetBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English Worksheets (16) - A Happy ChildDokument1 SeiteCBSE Class 1 English Worksheets (16) - A Happy ChildBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English Worksheets (17) - After A BathDokument1 SeiteCBSE Class 1 English Worksheets (17) - After A BathBOSS BOSSNoch keine Bewertungen
- Bhagwad GitaDokument6 SeitenBhagwad GitaBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English Worksheets (19) - Bubble, Straw and ShoeDokument2 SeitenCBSE Class 1 English Worksheets (19) - Bubble, Straw and ShoeBOSS BOSSNoch keine Bewertungen
- BuddhaDokument5 SeitenBuddhaBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English Worksheets (18) - After A BathDokument1 SeiteCBSE Class 1 English Worksheets (18) - After A BathBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English Assignments (1) - My Friends and GrammerDokument2 SeitenCBSE Class 1 English Assignments (1) - My Friends and GrammerBOSS BOSSNoch keine Bewertungen
- CBSE Class 1 English Worksheets 2 PDFDokument1 SeiteCBSE Class 1 English Worksheets 2 PDFnagsraviNoch keine Bewertungen
- Abraham LincolnDokument2 SeitenAbraham LincolnBOSS BOSSNoch keine Bewertungen
- TN HSC Physics Bookback One MarksDokument1 SeiteTN HSC Physics Bookback One MarksBOSS BOSSNoch keine Bewertungen
- Abdul Kal AmDokument3 SeitenAbdul Kal AmBOSS BOSSNoch keine Bewertungen
- Albert EinsteinDokument2 SeitenAlbert EinsteinBOSS BOSSNoch keine Bewertungen
- TN HSC Physics Bookback One MarksDokument1 SeiteTN HSC Physics Bookback One MarksBOSS BOSSNoch keine Bewertungen
- TN HSC Physics Bookback One MarksDokument1 SeiteTN HSC Physics Bookback One MarksBOSS BOSSNoch keine Bewertungen
- TN HSC Physics Bookback One MarksDokument1 SeiteTN HSC Physics Bookback One MarksBOSS BOSSNoch keine Bewertungen
- TN HSC Physics Bookback One MarksDokument1 SeiteTN HSC Physics Bookback One MarksBOSS BOSSNoch keine Bewertungen
- TN HSC Physics Bookback One MarksDokument1 SeiteTN HSC Physics Bookback One MarksBOSS BOSSNoch keine Bewertungen
- Conceptualizing On Structure Functionalism and Its Applications On Patriotism Study During Covid-19 Pandemic in MalaysiaDokument7 SeitenConceptualizing On Structure Functionalism and Its Applications On Patriotism Study During Covid-19 Pandemic in MalaysiaMuhammadSyaqirAimanNoch keine Bewertungen
- Basic Electrical Safety Module 1Dokument39 SeitenBasic Electrical Safety Module 1malawi200Noch keine Bewertungen
- MiningDokument3 SeitenMiningDherick RaleighNoch keine Bewertungen
- Ground Architecture (Mourad Medhat)Dokument146 SeitenGround Architecture (Mourad Medhat)Aída SousaNoch keine Bewertungen
- Engine Torque Settings and Spec's 3.0L V6 SCDokument4 SeitenEngine Torque Settings and Spec's 3.0L V6 SCMario MaravillaNoch keine Bewertungen
- Grade 8 - EnglishDokument2 SeitenGrade 8 - EnglishTCHR KIMNoch keine Bewertungen
- ASME Geometric Dimension Ing and Tolerance Professional CertificationDokument20 SeitenASME Geometric Dimension Ing and Tolerance Professional CertificationPaul Anthony Red60% (5)
- Communicative English Lab Manual 1643268175Dokument24 SeitenCommunicative English Lab Manual 1643268175Dimple BhatiNoch keine Bewertungen
- IES 2001 - I ScanDokument20 SeitenIES 2001 - I ScanK.v.SinghNoch keine Bewertungen
- Hamming Code - Error Detection Aim: AlgorithmDokument12 SeitenHamming Code - Error Detection Aim: Algorithmkrithikgokul selvamNoch keine Bewertungen
- The Research Problem: The Key Steps in Choosing A TopicDokument5 SeitenThe Research Problem: The Key Steps in Choosing A TopicJoachim San JuanNoch keine Bewertungen
- Evolis User ManualDokument28 SeitenEvolis User ManualIonmadalin1000Noch keine Bewertungen
- Chapter 2 Ag - EconDokument7 SeitenChapter 2 Ag - EconJay Kenneth Bajar Cernal100% (1)
- Conquering College The Most Fun You Can Have Learning The Things You Need To Know NodrmDokument144 SeitenConquering College The Most Fun You Can Have Learning The Things You Need To Know NodrmVithorNoch keine Bewertungen
- One Wavelength To Loop SkywireDokument2 SeitenOne Wavelength To Loop SkywireRobert TurnerNoch keine Bewertungen
- Burnay, Bushman & Laroi - 2019Dokument10 SeitenBurnay, Bushman & Laroi - 2019TinyjurshNoch keine Bewertungen
- Pradeep Kshetrapal - Genius Physics (Class 12) - For IIT-JEE and CBSE 2 - Libgen - LiDokument338 SeitenPradeep Kshetrapal - Genius Physics (Class 12) - For IIT-JEE and CBSE 2 - Libgen - Lisujan subediNoch keine Bewertungen
- Cable Systems For High and Extra-High Voltage: Development, Manufacture, Testing, Installation and Operation of Cables and Their AccessoriesDokument1 SeiteCable Systems For High and Extra-High Voltage: Development, Manufacture, Testing, Installation and Operation of Cables and Their AccessorieseddisonfhNoch keine Bewertungen
- Century Vemap PDFDokument5 SeitenCentury Vemap PDFMaster MirrorNoch keine Bewertungen
- SH5108 - 5 Occupational Health ProgrammeDokument34 SeitenSH5108 - 5 Occupational Health Programmetaaouicha mujahidNoch keine Bewertungen
- Motion in One Dimension QuestionDokument6 SeitenMotion in One Dimension Questionabh_omega33% (3)
- Anatomy & Physiology MCQsDokument26 SeitenAnatomy & Physiology MCQsMuskan warisNoch keine Bewertungen
- Statistical MethodsDokument77 SeitenStatistical MethodsGuruKPO100% (1)
- WebpdfDokument276 SeitenWebpdfprateekvNoch keine Bewertungen
- PienaDokument1 SeitePienaMika Flores PedroNoch keine Bewertungen
- Overleaf Keyboard ShortcutsDokument2 SeitenOverleaf Keyboard ShortcutsAlberto GiudiciNoch keine Bewertungen
- Advanced Laser Al170: Instruction ManualDokument35 SeitenAdvanced Laser Al170: Instruction ManualJuan Camilo100% (1)
- Chapter4 RetainingwallDokument55 SeitenChapter4 RetainingwallNur HazwaniNoch keine Bewertungen
- Om en A: F in Ite D Iffe Ren Ce-B Ase DN Um Eri Ca L M Eth Od SDokument426 SeitenOm en A: F in Ite D Iffe Ren Ce-B Ase DN Um Eri Ca L M Eth Od SPrateek Kumar PandeyNoch keine Bewertungen
- HVS Hotel Cost Estimating Guide 2021Dokument124 SeitenHVS Hotel Cost Estimating Guide 2021pascal rosasNoch keine Bewertungen
- Dark Matter and the Dinosaurs: The Astounding Interconnectedness of the UniverseVon EverandDark Matter and the Dinosaurs: The Astounding Interconnectedness of the UniverseBewertung: 3.5 von 5 Sternen3.5/5 (69)
- Quantum Spirituality: Science, Gnostic Mysticism, and Connecting with Source ConsciousnessVon EverandQuantum Spirituality: Science, Gnostic Mysticism, and Connecting with Source ConsciousnessBewertung: 4 von 5 Sternen4/5 (6)
- A Brief History of Time: From the Big Bang to Black HolesVon EverandA Brief History of Time: From the Big Bang to Black HolesBewertung: 4 von 5 Sternen4/5 (2193)
- A Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and ScienceVon EverandA Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and ScienceBewertung: 4 von 5 Sternen4/5 (51)
- Summary and Interpretation of Reality TransurfingVon EverandSummary and Interpretation of Reality TransurfingBewertung: 5 von 5 Sternen5/5 (5)
- Knocking on Heaven's Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern WorldVon EverandKnocking on Heaven's Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern WorldBewertung: 3.5 von 5 Sternen3.5/5 (64)
- Midnight in Chernobyl: The Story of the World's Greatest Nuclear DisasterVon EverandMidnight in Chernobyl: The Story of the World's Greatest Nuclear DisasterBewertung: 4.5 von 5 Sternen4.5/5 (410)
- Giza: The Tesla Connection: Acoustical Science and the Harvesting of Clean EnergyVon EverandGiza: The Tesla Connection: Acoustical Science and the Harvesting of Clean EnergyNoch keine Bewertungen
- Packing for Mars: The Curious Science of Life in the VoidVon EverandPacking for Mars: The Curious Science of Life in the VoidBewertung: 4 von 5 Sternen4/5 (1395)
- The Simulated Multiverse: An MIT Computer Scientist Explores Parallel Universes, The Simulation Hypothesis, Quantum Computing and the Mandela EffectVon EverandThe Simulated Multiverse: An MIT Computer Scientist Explores Parallel Universes, The Simulation Hypothesis, Quantum Computing and the Mandela EffectBewertung: 4.5 von 5 Sternen4.5/5 (20)
- Black Holes: The Key to Understanding the UniverseVon EverandBlack Holes: The Key to Understanding the UniverseBewertung: 4.5 von 5 Sternen4.5/5 (13)
- Quantum Physics: What Everyone Needs to KnowVon EverandQuantum Physics: What Everyone Needs to KnowBewertung: 4.5 von 5 Sternen4.5/5 (49)
- The Tao of Physics: An Exploration of the Parallels between Modern Physics and Eastern MysticismVon EverandThe Tao of Physics: An Exploration of the Parallels between Modern Physics and Eastern MysticismBewertung: 4 von 5 Sternen4/5 (500)
- The Beginning of Infinity: Explanations That Transform the WorldVon EverandThe Beginning of Infinity: Explanations That Transform the WorldBewertung: 5 von 5 Sternen5/5 (60)
- Strange Angel: The Otherworldly Life of Rocket Scientist John Whiteside ParsonsVon EverandStrange Angel: The Otherworldly Life of Rocket Scientist John Whiteside ParsonsBewertung: 4 von 5 Sternen4/5 (94)
- Too Big for a Single Mind: How the Greatest Generation of Physicists Uncovered the Quantum WorldVon EverandToo Big for a Single Mind: How the Greatest Generation of Physicists Uncovered the Quantum WorldBewertung: 4.5 von 5 Sternen4.5/5 (8)
- The Physics of God: How the Deepest Theories of Science Explain Religion and How the Deepest Truths of Religion Explain ScienceVon EverandThe Physics of God: How the Deepest Theories of Science Explain Religion and How the Deepest Truths of Religion Explain ScienceBewertung: 4.5 von 5 Sternen4.5/5 (23)
- Chernobyl 01:23:40: The Incredible True Story of the World's Worst Nuclear DisasterVon EverandChernobyl 01:23:40: The Incredible True Story of the World's Worst Nuclear DisasterBewertung: 4 von 5 Sternen4/5 (264)
- Lost in Math: How Beauty Leads Physics AstrayVon EverandLost in Math: How Beauty Leads Physics AstrayBewertung: 4.5 von 5 Sternen4.5/5 (125)
- The Sounds of Life: How Digital Technology Is Bringing Us Closer to the Worlds of Animals and PlantsVon EverandThe Sounds of Life: How Digital Technology Is Bringing Us Closer to the Worlds of Animals and PlantsBewertung: 5 von 5 Sternen5/5 (5)
- Bedeviled: A Shadow History of Demons in ScienceVon EverandBedeviled: A Shadow History of Demons in ScienceBewertung: 5 von 5 Sternen5/5 (5)
- The Reality Revolution: The Mind-Blowing Movement to Hack Your RealityVon EverandThe Reality Revolution: The Mind-Blowing Movement to Hack Your RealityBewertung: 4.5 von 5 Sternen4.5/5 (19)