Beruflich Dokumente
Kultur Dokumente
JJ205 Engineering Mechanic Chapter 4 Jj205
Hochgeladen von
Ah TiangOriginalbeschreibung:
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
JJ205 Engineering Mechanic Chapter 4 Jj205
Hochgeladen von
Ah TiangCopyright:
Verfügbare Formate
Dec-12
JJ205
ENGINEERING MECHANICS
CHAPTER 4
Structure Analysis
COURSE LEARNING OUTCOMES :
Upon completion of this course, students should be able to:
Prepared by:
Siti Syazwani Binti Ilmin
CLO 1. apply the principles of statics and dynamics to solve
engineering problems (C3)
CLO 2. sketch related diagram to be used in problem solving (C3)
CLO 3. study the theory of engineering mechanics to solve related
engineering problems in group (A3)
CLO 1. apply the principles of statics and dynamics to solve engineering problems (C3)
CLO 2. sketch related diagram to be used in problem solving (C3)
Introduction
Examples of Truss Structures
An engineering structure is any connected system of members built to
support or transfer forces and to safely withstand the loads applied to it.
Two types of engineering structures, plane truss and frame, will be
discussed in this lesson.
To determine the forces internal to an engineering structure, we must
dismember the structure and analyze separate free-body diagrams of
individual members or combinations of members.
In this statics class, only statically determinate structures, which do not
have more supporting constraints than are necessary to maintain an
equilibrium configuration, will be considered.
The analysis of trusses and frames under concentrated loads constitutes a
straightforward application of the material developed in the previous two
topics, force systems and equilibrium.
Dec-12
Definitions
Example of Truss Joint connection
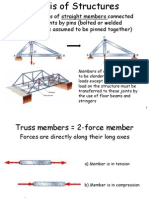
Trusses
Consist exclusively of straight
members connected at joints
located at the ends of each
member. Member of a truss,
therefore, are two-force
members that is, members each
acted upon by two equal and
opposite forces directed along
the member.
Gusset plate
Pin
Large bolt
5
1-Bridge (Figure 1a)
Planar Trusses
Lie in a single plane & are often used to
support roofs and bridges.
In the case of a bridge ,such as shown in
Figure 1a,the load on the deck is first
transmitted to stringers, then to floor
beams, & finally to the joints B,C, & D of
the two supporting side trusses.
The bridge truss loading is also coplanar,
like arrow in the Figure 1a.
C
B
Figure 1a
Figure 1b
7
Dec-12
Plane Trusses
2-Roof (Figure 1b)
Figure 1b is an example of a typical roofsupporting truss.
The roof load is transmitted to the truss at the
joint .
Since the imposed loading acts in the same
plane as the truss.
The analysis of the force developer in the truss
members is two dimensional.
9
Simple Truss
Truss - structure consisting of two-force members
(represented as pin connected) designed to support loads large
in comparison to its weight and applied at joints connecting
members
Simple trusses - build on triangles
simplest stable geometric shape
add two members and one joint at a time
Plane Trusses:
all members lie in a single plane
forces parallel to plane of truss, but not in the plane can
be transmitted via non-coplanar load bearing members
10
In contrast, the truss of figure (b), which
is made of three members connected by
pins at A, B, and C, will deform only
slightly under a load applied at B.
The truss of figure (b) is said to be rigid
truss, that is, the truss will not collapse.
Consider the truss of
figure (a), which are
made of four members
connected by pins at A,
B, C, and D.
As shown in figure (c), a larger rigid
truss can be obtained by adding two
members BD and CD to the basic
triangular truss of figure (b).
If a load applied at B, the
truss will greatly deform,
completely losing its
original shape.
A truss which can be constructed in this
manner is called simple truss.
11
12
Dec-12
Method of Joints
Techniques for Truss Analysis
Method of joints - usually used to determine
forces for all members of truss.
Method of sections - usually used to
determine forces for specific members of truss.
Do FBDs of the joints
Forces are concurrent at each joint no moments, just
Fx = 0 ,
Fy = 0
Procedure:
1) Choose joint with
at least one known force
at most two unknown forces
2) Draw FBD of the joint
draw just the point itself
draw all known forces at the point
assume all unknown forces are tension forces and
draw
positive results tension
negative results compression
13
14
Method of Sections
3) Solve for unknown forces by applying equilibrium
conditions in x and y directions:
Fx = 0 ,
Fy = 0
Do FBDs of sections of truss cut through various members.
Procedure:
1) Determine reaction forces external to truss system.
Draw FBD of entire truss.
Note: can find up to 3 unknown reaction forces.
Use Fx = 0, Fy = 0, M = 0 to solve for the
reaction forces.
2) Draw a section through the truss cutting no more than 3
members.
3) Draw an FBD of each section .one on each side of the cut.
Show external support reaction forces
Assume unknown cut members have tension forces
extending from them
4) Note: if the force on a member is known at one end,
it is also known at the other (since all forces are
concurrent and all members are two-force members)
5) Move to new joints and repeat steps 1-3 until all
member forces are known
15
16
Dec-12
Space Truss
4) Solve FBD for one section at a time using :
Fx = 0, Fy = 0, M = 0
When several
straight members
are joined together
at their extremities
to form a threedimensional
configuration, the
structure obtained is
called a space truss.
Note: choose pt for moments that isolates one
unknown if possible
5) Repeat with as many sections as necessary to find
required unknowns
17
The most elementary rigid
space truss consists of six
members joined at their
extremities to form the edges
of a tetrahedron ABCD (figure
(a)).
18
Frames
Designed to support loads.
Usually stationary, fully constrained
structures.
Frames always contains at least one multiforce
member, that is, a member acted upon by
three or more forces which, in general, are not
directed along the member.
By adding three members at a
time to this basic configuration,
such as AE, BE, and CE,
attaching them to three existing
joints, and connecting them at
a new joint, we can obtain a
larger rigid structure which is
defined as a simple space truss.
(figure (b)).
19
20
Dec-12
Analysis of Frames
Consider figure (a).
The crane is carried a given load W.
The free-body diagram of the
entire frame is shown in figure
(b).
Summing moments about A, we first determine
the force T exerted by the cable; summing x and
y components, we then determine the components
Ax and Ay of the reaction at the pin A.
This diagram can be used to
determine the external forces
acting on the frame.
21
22
First, the two-force member should be
considered.
In this frame, member BE is the only twoforce member.
The forces acting at each end of this
member must have; same magnitude,
same line of action, and opposite sense.
They are therefore, directed along BE and
will be denoted, respectively by FBE and
FBE.
Their sense is as in the figure shown.
later, the sign obtained for the common
magnitude FBE of the two forces will
confirm or deny this assumption.
In order to determine the internal forces
holding the various parts of a frame together,
we must dismember the frame and draw FBD
for each of its components parts.
23
24
Dec-12
Next, consider the multiforce members, which is the
members which acted upon by three or more forces.
They have same magnitude FBE and opposite
sense.
According to Newtons third law, the force exerted at B
by member BE on member AD must be equal and
opposite to the force FBE exerted by AD on BE.
force exerted at B by
member BE on member AD
Similarly, the force exerted at E by member BE on
member CF must be equal and opposite the force FBE
exerted by CF on BE.
the force
exerted at E
by member
BE on
member CF
Thus, the forces that the two-force member BE exerts
on AD and CF are respectively, equal to FBE and FBE.
25
At C, two multiforce members are
connected.
Since, neither the direction nor the
magnitude of the forces acting at C is
known, these forces will be
represented by their x and y
components.
The components Cx and Cy of the
force acting on member AD will be
arbitrarily directed to the right and
upward.
27
26
Since, according to Newtons third law, the
forces exerted by member CF on AD and by
member AD on CF, are equal and opposite.
The components of the force acting on
member CF must be directed to the left and
downward.
They will be denoted respectively, by - Cx and
-Cy .
28
Dec-12
Whether the force Cx is actually directed to
the right and the force Cx is actually directed
to the left will be determined later from the
sign of their common magnitude Cx.
The internal forces can now be determined by
considering the FBD of either of the two
multiforce member.
A plus sign indicating that the assumption
made was correct and a minus sign that it was
wrong.
Choosing the FBD of CF, for example, we
write the equations MC=0, ME=0 and
Fx=0, which yield the values of the
magnitudes FBE, Cy, and Cx, respectively.
The FBD of the multiforce members are
completed by showing the external forces
acting at A, D, and F.
These values can be checked by verifying that
member AD is also in equilibrium.
29
30
For example: a pair of cutting pliers used to
cut a wire.
Machines
Designed to transmit and
modify forces and are structures
containing moving parts.
Machines like frames, always
contain at least one multiforce
member.
Whether they are simple tools
or include complicated
mechanisms, their main
purpose is to transform input
forces into output forces.
If we apply two equal and opposite forces P
and P on their handles, they will exert two
equal and opposite forces Q and Q on the
wire.
31
32
Dec-12
To determine the magnitude Q of the output
forces when the magnitude P of the input
forces is known (or, conversely, to determine P
when Q is known);
However, since a pair of pliers forms a nonrigid
structure, use one of the component parts as a
free body in order to determine the unknown
forces.
Draw FBD of the pliers alone, showing the input
forces P and P and the reactions Q and Q that
the wire exerts on the pliers.
33
For example;
Taking moments about A.
The relationship Pa = Qb is obtained, which
defines the magnitude Q in terms of P or P in terms
of Q.
The same FBD can be used to determine the
components of the internal force at A; Ax = 0 and
Ay = P + Q can be found.
35
34
In the case of more complicated machines, it
generally will be necessary to use several FBD
and, possibly, to solve simultaneous equations
evolving various internal forces.
The free bodies should be chosen to include
the input forces and the reactions to the
output forces, and the total number of
available independent equations.
Before attempting to solve a problem,
determine whether the structure considered
is determinate.
36
Das könnte Ihnen auch gefallen
- HRA2 Service ManualDokument59 SeitenHRA2 Service ManualuserrnNoch keine Bewertungen
- JJ310 STRENGTH OF MATERIAL Chapter 4 (A) Bending StressDokument16 SeitenJJ310 STRENGTH OF MATERIAL Chapter 4 (A) Bending StressAh Tiang50% (2)
- Tormax Automatic Sensor 7501Dokument12 SeitenTormax Automatic Sensor 7501name familyNoch keine Bewertungen
- Jmi Telephone Directory 2022Dokument107 SeitenJmi Telephone Directory 2022Prince Soni XII D 21Noch keine Bewertungen
- PalmistryDokument115 SeitenPalmistryverne4444100% (3)
- Math 216 SyllabusDokument4 SeitenMath 216 Syllabusdoney_78100% (1)
- MUFON UFO Journal - December 1997Dokument24 SeitenMUFON UFO Journal - December 1997Carlos RodriguezNoch keine Bewertungen
- Experimental Design Graphic OrganizerDokument2 SeitenExperimental Design Graphic OrganizerApplesauce90Noch keine Bewertungen
- Chapter 5 Analysis of StructureDokument20 SeitenChapter 5 Analysis of StructureRenu SekaranNoch keine Bewertungen
- TrussDokument18 SeitenTrussSYifa ShuhaIliNoch keine Bewertungen
- Structural Analysis: Engr. John Marco I. MatiraDokument28 SeitenStructural Analysis: Engr. John Marco I. MatiraAIMNoch keine Bewertungen
- Lecture 7, 8, 9 - Chapter 4 Analysis of StructuresDokument57 SeitenLecture 7, 8, 9 - Chapter 4 Analysis of Structuresrobel metikuNoch keine Bewertungen
- Chapter 3: Structures: TrussesDokument19 SeitenChapter 3: Structures: TrussesBadar Sharif100% (1)
- Lecture 4-3Dokument51 SeitenLecture 4-3katethekat2.0Noch keine Bewertungen
- MECH100 Lecture Chapter 4Dokument42 SeitenMECH100 Lecture Chapter 4Kristina PonceNoch keine Bewertungen
- IntroductionDokument17 SeitenIntroductionPhyo ZawNoch keine Bewertungen
- 5 - Structural AnalysisDokument46 Seiten5 - Structural AnalysisHawsar Omer HamaNoch keine Bewertungen
- Dapdap StatDokument7 SeitenDapdap StatDanisse LoiNoch keine Bewertungen
- Statics Notes 4 For StudentsDokument24 SeitenStatics Notes 4 For Students왕흠일Noch keine Bewertungen
- Chapter 6 Analysis of Structures: Connected at Their Extremities Only. The Members BeingDokument13 SeitenChapter 6 Analysis of Structures: Connected at Their Extremities Only. The Members BeingBELAL ALSUBARINoch keine Bewertungen
- Mechanics CH-4 MarkosDokument13 SeitenMechanics CH-4 MarkosGadisaNoch keine Bewertungen
- 16 Lecture Notes For Sections 6.1-6.3Dokument11 Seiten16 Lecture Notes For Sections 6.1-6.3iking balonNoch keine Bewertungen
- LECTURE 3 - StructuresDokument31 SeitenLECTURE 3 - StructuresALBERT MALIRONoch keine Bewertungen
- Chapter 4.a (Simple Truses)Dokument24 SeitenChapter 4.a (Simple Truses)LogarithemNoch keine Bewertungen
- CHAPTER 5 Structural AnalysisDokument76 SeitenCHAPTER 5 Structural AnalysisDavid MurphyNoch keine Bewertungen
- Chapter 6 Structural AnalysisDokument30 SeitenChapter 6 Structural AnalysisOmar AbdullahNoch keine Bewertungen
- Zero Force MemberDokument2 SeitenZero Force MemberNkosinathi EphraimNoch keine Bewertungen
- Analysis of Trusses: Vector Mechanics For Engineers: StaticsDokument31 SeitenAnalysis of Trusses: Vector Mechanics For Engineers: StaticsAlex CarrilloNoch keine Bewertungen
- Truss Lecture6xDokument28 SeitenTruss Lecture6xJoe JoeNoch keine Bewertungen
- Analysis of Simple Trusses: - Prof. Amba ShettyDokument51 SeitenAnalysis of Simple Trusses: - Prof. Amba ShettyShilpashree VNoch keine Bewertungen
- Engineering MechanicsDokument80 SeitenEngineering MechanicsVv4H100% (1)
- Connected at Their Extremities Only. The Members BeingDokument13 SeitenConnected at Their Extremities Only. The Members BeingMarco AntonioNoch keine Bewertungen
- Note Chapter 6.1 - 6.4Dokument32 SeitenNote Chapter 6.1 - 6.4Syakir ImanNoch keine Bewertungen
- Strength of MaterialsDokument26 SeitenStrength of MaterialsJohn Kristoffer GimpesNoch keine Bewertungen
- Analysis of Plane Trusses: Dr. Arkadeb Mukhopadhyay Department of Mechanical EngineeringDokument23 SeitenAnalysis of Plane Trusses: Dr. Arkadeb Mukhopadhyay Department of Mechanical EngineeringAayush SinghNoch keine Bewertungen
- Connected at Their Extremities Only. The Members BeingDokument13 SeitenConnected at Their Extremities Only. The Members BeingSergio Sánchez SalazarNoch keine Bewertungen
- Structures: Unit IIIDokument27 SeitenStructures: Unit IIIDivyanshuVermaNoch keine Bewertungen
- Week 6 - Frames+Friction+FluidDokument60 SeitenWeek 6 - Frames+Friction+Fluidiwhy_Noch keine Bewertungen
- Chapter 05Dokument41 SeitenChapter 05Bảo Tín TrầnNoch keine Bewertungen
- TRUSSDokument11 SeitenTRUSSJanice RamonNoch keine Bewertungen
- Truss Rigid FramesDokument13 SeitenTruss Rigid Framessensei_sembeyNoch keine Bewertungen
- TrussDokument13 SeitenTrussArjun Sharma VNoch keine Bewertungen
- MachineFrames SplitDokument70 SeitenMachineFrames SplitRavi TilaganjiNoch keine Bewertungen
- Lecture 2 Analysis of Trusses Arki 3Dokument44 SeitenLecture 2 Analysis of Trusses Arki 3Michaela Vernice PeñarubiaNoch keine Bewertungen
- Section 2Dokument42 SeitenSection 2tryjasmitNoch keine Bewertungen
- Lec 3 - MTD of Sections - TrussDokument27 SeitenLec 3 - MTD of Sections - TrussIsrar KhanNoch keine Bewertungen
- Adapted From: Vector Mechanics For Engineers: Statics by Ferdinand Beer and Russel JohnstonDokument26 SeitenAdapted From: Vector Mechanics For Engineers: Statics by Ferdinand Beer and Russel Johnston공명형Noch keine Bewertungen
- JJ205 Engineering Mechanic Chapter 3 Jj205Dokument5 SeitenJJ205 Engineering Mechanic Chapter 3 Jj205Ah TiangNoch keine Bewertungen
- Dr. Arafa S.Sobh: InstructorDokument50 SeitenDr. Arafa S.Sobh: InstructorAbdelhay Mohamed Hassan100% (1)
- Engineering Mechanics I CHAP 4Dokument9 SeitenEngineering Mechanics I CHAP 4nvnrevNoch keine Bewertungen
- Engineering Mechanics (Analysis of Trusses)Dokument5 SeitenEngineering Mechanics (Analysis of Trusses)Ema MiguelNoch keine Bewertungen
- Method of JoinDokument45 SeitenMethod of JoinkhairulhakamNoch keine Bewertungen
- Diagrama Del Cuerpo Libre - EstáticaDokument13 SeitenDiagrama Del Cuerpo Libre - Estáticaabrahamrv44Noch keine Bewertungen
- Structures: ENGG1960Dokument34 SeitenStructures: ENGG1960Sahil GrewalNoch keine Bewertungen
- Ayush Kishore 21410005 Physics ProjectDokument12 SeitenAyush Kishore 21410005 Physics ProjectAYUSH KISHORENoch keine Bewertungen
- 3.0 Trusses and FrictionDokument28 Seiten3.0 Trusses and FrictionwengsungNoch keine Bewertungen
- 3-Analysis of StructuresDokument42 Seiten3-Analysis of StructuresJoylyn BeranNoch keine Bewertungen
- Chapter 1 - Method of JointDokument45 SeitenChapter 1 - Method of JointJNoch keine Bewertungen
- Simple Truss PDFDokument14 SeitenSimple Truss PDFHalesh NaikNoch keine Bewertungen
- Simple Truss PDFDokument14 SeitenSimple Truss PDFHalesh NaikNoch keine Bewertungen
- 01 SIMPLE TRUSSES DR G. S KameDokument21 Seiten01 SIMPLE TRUSSES DR G. S KameDrGanesh KameNoch keine Bewertungen
- Week 14 Coe 112 Module (20231130212210)Dokument20 SeitenWeek 14 Coe 112 Module (20231130212210)channelmindNoch keine Bewertungen
- TrussDokument7 SeitenTrussa_j_sanyal259Noch keine Bewertungen
- CE 3221 (Truss)Dokument21 SeitenCE 3221 (Truss)shuvo devNoch keine Bewertungen
- Analysis of StructuresDokument18 SeitenAnalysis of StructuresVivo 1906Noch keine Bewertungen
- Week 5 TrussesDokument40 SeitenWeek 5 Trussesiwhy_Noch keine Bewertungen
- JJ310 STRENGTH OF MATERIAL Chapter 6 TorsionDokument21 SeitenJJ310 STRENGTH OF MATERIAL Chapter 6 TorsionAh Tiang0% (1)
- JJ310 STRENGTH OF MATERIAL Chapter 5 (B) Beam DeflectionDokument18 SeitenJJ310 STRENGTH OF MATERIAL Chapter 5 (B) Beam DeflectionAh TiangNoch keine Bewertungen
- JJ303 Report TigDokument10 SeitenJJ303 Report TigAh Tiang67% (9)
- JJ308 REPORT Layout and Piping of The Steam Power Plant SystemDokument9 SeitenJJ308 REPORT Layout and Piping of The Steam Power Plant SystemAh Tiang86% (7)
- JJ310 STRENGTH OF MATERIAL Chapter 5 (A) Beam DeflectionDokument20 SeitenJJ310 STRENGTH OF MATERIAL Chapter 5 (A) Beam DeflectionAh TiangNoch keine Bewertungen
- JJ310 STRENGTH OF MATERIAL Chapter 4 (B) Bending StressDokument14 SeitenJJ310 STRENGTH OF MATERIAL Chapter 4 (B) Bending StressAh TiangNoch keine Bewertungen
- JJ310 STRENGTH OF MATERIAL Chapter 3 (A) Shear Force & Bending Moment ADokument22 SeitenJJ310 STRENGTH OF MATERIAL Chapter 3 (A) Shear Force & Bending Moment AAh TiangNoch keine Bewertungen
- JJ310 STRENGTH OF MATERIAL Chapter 1 (A) Forces On MaterialDokument18 SeitenJJ310 STRENGTH OF MATERIAL Chapter 1 (A) Forces On MaterialAh Tiang100% (1)
- JJ310 STRENGTH OF MATERIAL Chapter 2 Thermal Stresses and Composite BarsDokument20 SeitenJJ310 STRENGTH OF MATERIAL Chapter 2 Thermal Stresses and Composite BarsAh Tiang50% (6)
- JJ310 STRENGTH OF MATERIAL Chapter 1 (B) Forces On MaterialDokument20 SeitenJJ310 STRENGTH OF MATERIAL Chapter 1 (B) Forces On MaterialAh TiangNoch keine Bewertungen
- JJ311 MECHANICAL OF MACHINE CH 4 FrictionDokument12 SeitenJJ311 MECHANICAL OF MACHINE CH 4 FrictionAh Tiang100% (2)
- JJ311 MECHANICAL OF MACHINE CH 5 BalancingDokument26 SeitenJJ311 MECHANICAL OF MACHINE CH 5 BalancingAh Tiang33% (3)
- JJ306 Autodesk Inventor Week 2 - Project 2 - Flange Manifold PartDokument42 SeitenJJ306 Autodesk Inventor Week 2 - Project 2 - Flange Manifold PartAh TiangNoch keine Bewertungen
- JF302 Material Technology Topic 4 Mechanical TestDokument4 SeitenJF302 Material Technology Topic 4 Mechanical TestAh TiangNoch keine Bewertungen
- JJ311 MECHANICAL OF MACHINE CH 3 Velocity and Acceleration DiagramDokument31 SeitenJJ311 MECHANICAL OF MACHINE CH 3 Velocity and Acceleration DiagramAh Tiang100% (1)
- JJ311 Mechanical of Machine CH 1 HoistDokument15 SeitenJJ311 Mechanical of Machine CH 1 HoistAh Tiang100% (3)
- BA201 Engineering Mathematic UNIT7 - Matrices OperationDokument28 SeitenBA201 Engineering Mathematic UNIT7 - Matrices OperationAh TiangNoch keine Bewertungen
- JJ311 MECHANICAL OF MACHINE CH 2 Simple Harmonic MotionDokument38 SeitenJJ311 MECHANICAL OF MACHINE CH 2 Simple Harmonic MotionAh Tiang100% (3)
- JJ306 Autodesk Inventor Week 2 - Project 3 - Air Cover PartDokument21 SeitenJJ306 Autodesk Inventor Week 2 - Project 3 - Air Cover PartAh TiangNoch keine Bewertungen
- JF302 Material Technology TOPIC 1 Material Structure and Binary Alloy SystemDokument26 SeitenJF302 Material Technology TOPIC 1 Material Structure and Binary Alloy SystemAh TiangNoch keine Bewertungen
- BA201 Engineering Mathematic UNIT2 - Measures of Central TendencyDokument19 SeitenBA201 Engineering Mathematic UNIT2 - Measures of Central TendencyAh TiangNoch keine Bewertungen
- PassYear - JJ207 Thermodynamic - SesiJun2012Dokument7 SeitenPassYear - JJ207 Thermodynamic - SesiJun2012Ah TiangNoch keine Bewertungen
- BA201 Engineering Mathematic UNIT8 - Cramer's Rule and Inverse Matrix MethodDokument14 SeitenBA201 Engineering Mathematic UNIT8 - Cramer's Rule and Inverse Matrix MethodAh TiangNoch keine Bewertungen
- +2 Physics Practical Readings 2019-2020Dokument11 Seiten+2 Physics Practical Readings 2019-2020Barkath Shalu100% (1)
- 6FC5303-0AF35-0AA0 Datasheet enDokument1 Seite6FC5303-0AF35-0AA0 Datasheet ennathansta61Noch keine Bewertungen
- Pseudo-Static Master-Slave Match-Line Scheme For Sustainable-Performance and Energy-Efficient Content Addressable MemoryDokument4 SeitenPseudo-Static Master-Slave Match-Line Scheme For Sustainable-Performance and Energy-Efficient Content Addressable MemoryTajbia HossainNoch keine Bewertungen
- Power Imbalance Issues in AdvertisingDokument22 SeitenPower Imbalance Issues in AdvertisingIonut IugaNoch keine Bewertungen
- Data Science Assignment 01Dokument4 SeitenData Science Assignment 01Abdul MAalikNoch keine Bewertungen
- Workshop Manual: Group 30 Electrical System IDokument176 SeitenWorkshop Manual: Group 30 Electrical System Irichard castañeda100% (1)
- Aa - Spec - 538011 Medium Voltage Induction MotorsDokument32 SeitenAa - Spec - 538011 Medium Voltage Induction Motorsjonodo89Noch keine Bewertungen
- Using Engineering and Management Principles For Better Patient Care Nikhil BalakrishnanDokument345 SeitenUsing Engineering and Management Principles For Better Patient Care Nikhil BalakrishnanYendy ReyesNoch keine Bewertungen
- Cummins K50 Engine Spare Parts Catalog: Part Number DescriptionDokument46 SeitenCummins K50 Engine Spare Parts Catalog: Part Number DescriptionPM Gen careNoch keine Bewertungen
- Unit 8 Migration: 8.0 ObjectivesDokument10 SeitenUnit 8 Migration: 8.0 ObjectivesSatyanshNoch keine Bewertungen
- Aquatherm NA 2014Dokument137 SeitenAquatherm NA 2014Heather MurphyNoch keine Bewertungen
- Predominance Area DiagramDokument5 SeitenPredominance Area Diagramnaresh naikNoch keine Bewertungen
- Tienlongtech-So Tay Ac Quy PanasonicDokument75 SeitenTienlongtech-So Tay Ac Quy PanasonicThuận LêNoch keine Bewertungen
- Ise Online Access For Introduction To Operations Research 11Th Edition Hillier Full ChapterDokument51 SeitenIse Online Access For Introduction To Operations Research 11Th Edition Hillier Full Chapterdarrell.berry639100% (4)
- JVC KD r540 Manual de InstruccionesDokument16 SeitenJVC KD r540 Manual de InstruccionesJesus FloresNoch keine Bewertungen
- How To Kill It at Law School - Harshil Vijayvargiya-Pages-8-15Dokument8 SeitenHow To Kill It at Law School - Harshil Vijayvargiya-Pages-8-15VANSH CHOUHANNoch keine Bewertungen
- Sensors: Performance Evaluations of Lora Wireless Communication in Building EnvironmentsDokument19 SeitenSensors: Performance Evaluations of Lora Wireless Communication in Building EnvironmentsN sartikaNoch keine Bewertungen
- Aeronautics: Aeronautical Calculations: What's With All Those Coefficients Anyway?Dokument2 SeitenAeronautics: Aeronautical Calculations: What's With All Those Coefficients Anyway?Baldev RamNoch keine Bewertungen
- Doménech Carbó Osete Cortina2016 - Article - AnotherBeautyOfAnalyticalChemiDokument50 SeitenDoménech Carbó Osete Cortina2016 - Article - AnotherBeautyOfAnalyticalChemigmjNoch keine Bewertungen
- Vce Chemistry Unit 3 Sac 2 Equilibrium Experimental Report: InstructionsDokument5 SeitenVce Chemistry Unit 3 Sac 2 Equilibrium Experimental Report: InstructionsJefferyNoch keine Bewertungen
- Lyapunov Function - Dynamical SystemsDokument4 SeitenLyapunov Function - Dynamical SystemsmCmAlNoch keine Bewertungen
- Position, Velocity and AccelerationDokument12 SeitenPosition, Velocity and AccelerationawbNoch keine Bewertungen
- Shotcrete Solutions PDFDokument2 SeitenShotcrete Solutions PDFBrett HartNoch keine Bewertungen