Beruflich Dokumente
Kultur Dokumente
Taylor Series For Inverse Laplace
Hochgeladen von
Gustavo MiottoOriginaltitel
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Taylor Series For Inverse Laplace
Hochgeladen von
Gustavo MiottoCopyright:
Verfügbare Formate
Graded-index multimode fibre is used for the delay lines since
the multimode 1 x 7 optical splitter and the 7 x 1 optical
combiner are readily available.
A data bit T is continuously sent by stations 1 to 14 in
arbitrary time slots by suitable delaying the clock as shown in
Fig. 2. Data are sent by a 15th station in the 33rd slot (also
chosen arbitrarily) using a Ti:LiNbO 3 Mach-Zehnder type
interferometric integrated electro-optic modulator, which
requires polarised input light. A fibre polarisation controller5
is used to adjust the input polarisation state. The polarisation
controller introduces a loss of <0-5dB and the modulator
introduces a loss of 7 dB.
The fused biconical multimode star coupler combines the
signals from the 15 stations. An optical receiver retrieves the
data by delaying the clock to the 33rd slot and adding it to
the TDMA signal, using a multimode 2 x 2 coupler. Fig. 3
shows the oscilloscope traces of the clock, the TDMA frame
with the clock pedestal, and the recovered data. The clock
amplitude is set equal to the signal amplitude.
Conclusion: A fixed assignment TDMA fibre-optic system
with 50 assignable time slots and optical synchronisation was
implemented at lOMbit/s (2ns slots), and <10" 9 BER was
measured. The feasibility of the protocol was demonstrated
with 15 active stations (14 interferers and pseudorandom
data). In the future, the Lightwave Communications Laboratory at Columbia University will incorporate a mode-locked
Nd:YAG laser in the TDMA network, generating 140 ps
pulses at 1-32/mi with peak pulse powers of 150 W. This will
allow up to 500 active stations transmitting at 14Mbit/s.
Nonlinear optical effects may be avoided by coupling the laser
light directly into a bundle offibres.The data regeneration
process will also be done optically, using optical bistable
devices, to reduce the electronic bandwidth requirement of the
receiver.
Acknowledgments: The authors wish to thank Dr. M. Corke of
Amphenol Fibre Optics Products and L. W. Stulz of AT&T
Bell Laboratories for providing some optical components. The
assistance of D. J. Blumenthal and M. Levy of the Lightwave
Communications Laboratory is also acknowledged.
P. R. PRUCNAL
M. A. SANTORO
S. K. SEHGAL
Lightwave Communications Laboratory
Center for Telecommunications Research
Columbia University
New York, NY 10027, USA
16th September 1986
I. P. KAMINOW
AT&T Bell Laboratories
Crawford Hill Laboratory
Holmdel, NJ 07733, USA
Fig. 3
a Optical clock synchronised to 33rd slot with 2 ns pulses at
10 MHz
b TDMA frame sequence at photodetector output showing 14
interfering ones and data sequence in 33rd slot. Ones in slot 33 are
raised on the clock pedestal, whereas zeros in slot 33 do not appear
on the clock pedestal
c Recovered data (one is low, zero is high) at monostable multivibrator output 10101000100011101010
A lOMbit/s pseudorandom word pattern is generated by a
bit-error-rate (BER) test set and transmitted in the 33rd time
slot. BERs better than 10" 9 are measured, verifying that,
given this laser pulse energy, excess optical loss and receiver
sensitivity, 15 stations can indeed be accommodated in the
TDMA system. With an increase in laser pulse energy, the
number of stations can be increased in accordance with
eqn. 1.
TAYLOR SERIES APPROACH TO
FUNCTIONAL APPROXIMATION FOR
INVERSION OF LAPLACE TRANSFORMS
Indexing terms: Control theory, Laplace transforms, Taylor
series, Inverse Laplace transforms
The letter is devoted to a functional approximation for inversion of the Laplace transform. The function is approximated
by a truncated Taylor series, which is expanded about t 0 = 0.
Utilising a special transformation, each Laplace transform is
converted into a set of simultaneous linear algebraic equations which are then easily computed to give the coefficients
of the basis function. Two examples with satisfactory results
are given.
Introduction: As is well known, the Laplace transform method
has found wide applications in many engineering problems.
However, it is sometimes very difficult to obtain inversion of
the Laplace transform. It is not a trivial matter, particularly
for transcendental functions whose inversions are not given in
tables of Laplace transforms.
In the past, the inversion of Laplace transforms via orthogonal functions has been discussed by many researchers. Chen
et al.1 first considered fractional calculus for inverting irratio-
References
1
DA VIES, P. W., BARBER, D. L. A., PRICE, W. L., a n d SOLOMONIDES, C. M.:
'Computer networks and protocols' (John Wiley & Sons, New
York, 1981), Chap. 5
2
PRUCNAL, p. R., SANTORO, M. A., and FAN, T. R.: 'Spread spectrum
fiber optic local area network using optical processing', J. Lightwave Technoi, 1986, 4, pp. 547-554
3
PRUCNAL, P. R., SANTORO, M. A., and SEHGAL, s. K.: 'Ultra-fast all-
optical synchronous multiple access fiber networks', J. Lightwave
Technoi. and IEEE J. Sel. Areas in Commun. (joint special issue),
to be published
4
GOTO, H., NAGASH1MA, K., SUZUKI, S., KONDO, M., a n d OHTA, Y.:
'Optical time-division digital switching: an experiment'. OS A/
IEEE sixth topical meeting on optical fiber communications, New
Orleans, 28 Feb.-l March 1983
5 LEFEVRE, H. c.: 'Single-mode-fibre fractional-wave devices and polarisation controllers', Electron. Lett., 1980,16, p. 778
nal Laplace transforms using Walsh functions, and its related
block pulse functions have been extensively applied to the
inversion of rational and irrational Laplace transforms.2"4
Instead, their results are piecewise constant. More recently,
the application of shifted Chebyshev series5 has been studied
from piecewise constant orthogonal functions to continuous
orthogonal polynomials. However, it needs more computation
time to calculate the coefficients of a basis function through
using recursive forms. The objective of this letter is to obtain a
more effective and simple procedure for inverting rational and
transcendental Laplace transforms via the Taylor series
approach. As Bellman et al.6 have pointed out, no completely
general and satisfactory numerical inversion formula exists for
the Laplace transform; consequently, different numerical techniques should be studied for the purpose of solving particular
classes of common control problems. It is this idea that has
motivated the work introduced herein. Two numerical examples are given to show the effectiveness of the present method.
Taylor polynomials: A function y = y(t) which is analytic in
the neighbourhood of the point 10 = 0 may be expanded into
a power series using the Maclaurin formula
ELECTRONICS LETTERS 6th November 1986 Vol. 22 No. 23
(i)
n= 0
1219
where
where a( are coefficients to be determined. Next, multiplying
eqn. 10 by fj{t) exp ( t/k) and integrating from 0 to oo gives
'*>-
'-h&
(2)
y(t)fft)exp(-t/k)dt
With the view of obtaining an approximate expression of the
analytic function y(t) over the interval (0, T), where y(t) may
be assumed analytic, one can truncate the series of eqn. 1 up
to the mth term:
00
m-1
= I , fi
exp (-t/k) dt
;=o J
(3)
j = 0,l,2,...,m-l
(11)
Invoking eqn. 9, eqn. 11 can be rewritten as
or
00
y(t) ~ aTJ[t)
(4)
,0 %<*. = fJj
(12)
where
<xT = [ a 0 , a l s . . . , a m _ j "
By the definition of the Laplace transform, a function y(t) is
given as
and
fT(t) = IMtlUt),....
/_,()] = [i, t, t\ ..., r - 1 ]
y(t) exp (-st) dt = Y(s)
Here, f(t) is the called basis function vector. In general, the
function basis is written as
(13)
Letting; = 0,1,2,..., one has
y(t)exp(-t/k)fo(t)dt=Y(l/k)
(5)
y(t)txv(-t/k)fl(t)dt=Y(2/k)
At this point, integrating ft{z)fj(z) from z = 0 to z = 1, one
obtains
(14)
y(t)txp(-t/k)f2(t)dt=Y(3/k)
^fi(z)fJ{z)dz = - ~ ^
(6)
In an effort to invert the Laplace transforms, the domain has
to be transformed into values between 0 and infinity. Let
z = exp ( t/k)
0 < t < oo
(7)
where k is an adjustable positive parameter; for convenience,
k = 1 is selected for implementation. Therefore, the basis function becomes
cxp(-t/k)
exp(-2t/k)
Then, eqns. 12 and 14 form a set of m simultaneous linear
algebraic equations which are used to calculate <x0, al5 . . . ,
a m _j. Once the af have been determined, the functional
approximation for the inverse Laplace transform can be
obtained from eqn. 10.
Numerical examples:
(a) Example 1: Consider the following rational transfer function:
fo(t) = 1
=
y(t)txp(-t/k)fJ{t)dt=Y(j+l/k)
(8)
Y(s) = A/s(s + 2)
From eqns. 12 and 14, one constructs a set of simultaneous
linear algebraic equations for m = 3 and k = 1:
from which it is seen that the constant k has the function of
regulating the response speed.
Inserting eqn. 7 into eqn. 6, one obtains a useful formula for
inverting Laplace transforms as
a, + (l/3)a2 = 4/3
(l/2)a0 + (1/3)01! + (l/4)a2 = 1/2
(15)
00
(9)
By the solution of eqn. 15, one obtains a0, al5 a2 as
a0 = 2
Obtaining inverse Laplace transforms: Any finite function y(t)
can be represented by a series expansion. In this method, the
function is denoted as a Taylor polynomial:
at = 0
a2 = - 2
Therefore the inverse Laplace transform of Y(s) is
y(t) = 2 2 exp ( 20
(10)
1220
This is precisely the same as the exact solution of y(t).
ELECTRONICS LETTERS 6th November 1986
Vol. 22 No. 23
Introduction: Exact analysis of fused couplers is a formidable
task since it requires the exact solution of the 2-D vector wave
equation. Therefore, many discussions on fused couplers are
limited to those of rectangular cross-section, for which
approximate analytical results are available.1"3 Recently,
Snyder and Zheng, making use of their asymptotic solution
for the Maxwell equations,4 have derived very simple expressions for fused couplers of various cross-sectional shapes.5
However, the accuracy of their results5 at finite V has not
been confirmed since they are exact only at infinite V, where
V is the normalised frequency. Moreover, the derivation of
such formulas requires the solution of the 2-D scalar wave
equation in an arbitrarily bounded domain and the computation of the normal derivative of the scalar field on the boundary. These calculations are in general quite cumbersome.6
In this letter the effective-index method, which was developed for the analysis of optical waveguides of general crosssection,7"9 is applied to the analysis of fused couplers. The
method is very simple and highly efficient. Results for rectangular and elliptical couplers are compared with those given
by the asymptotic analysis.4-5 A stadium-shaped coupler,
which models the realistic one, is also analysed by the present
method.
(b) Example 2: Consider the following problem, whose transcendental transfer function1 is given as
Y(s) = (l/s)exp(-s/s+l)
Likewise, taking m = 3 and k = 1, the coefficients are found
by using eqns. 12 and 14 as
a o = 0-9211
a t = 0-768
a 2 = 0-21
Consequently, y{t) is obtained as
y(t) = 0-9211 - 0-768 exp ( - f ) + 0-21 exp (-2t)
For comparison, the exact solution, the Chebyshev approach
and the proposed method are shown in Table 1. The agreement is quite satisfactory.
Table 1 COMPARISON OF SOLUTIONS
FOR EXAMPLE 2
t
Exact
Taylor
Chebyshev
(Chou et al.5)
00
0-4
0-8
1-2
1-6
20
0-3678
0-5009
0-6086
0-6948
0-7633
0-8172
0-3631
0-5007
0-6184
0-7089
0-7746
0-8210
0-3828
0-4937
0-6083
0-7032
0-7749
0-8267
Method: A coupler is characterised by the polarisationdependent coupling coefficients Cx = (/Ju /?2i)/2 and Cy =
(fii - 0$i)A 2 ' 5 where ftx (flO and F2l (0>2l) are the propagation constants for the E\i (Eyu) and 21 (21) modes of the
coupler, respectively. Here, modes are designated according to
Goell's method.10 Since a typical fused coupler is operated at
V P I,2 the mode field in the coupler is approximately uniformly polarised.4 This consideration makes it possible to use
the effective-index method7"9 to accurately determine the propagation constants and hence the coupling coefficients of the
coupler, which can be of arbitrary shape.
The basic principle of the effective-index method is to
reduce, approximately, the 2-D wave equation into 1-D wave
equations which can be solved easily.7"9 We consider a fused
coupler with long axis 2a and short axis 2b as shown in
Fig. la. At x = x,, the thickness of the coupler is given by
2t(xi). The propagation constant for the TEn_x
(JMn_^)
mode of the infinite slab of thickness 2t(x), with index nx
sandwiched between two semi-infinite layers of index n2, is
used to define the effective-index function nx(x). The propagation constant for the TMm-x (TE^i) mode of the infinite
slab of thickness 2a, with index profile nx(x), is then the
approximate propagation constant for the * (^) mode of
the coupler. In many cases, nx(x) being analytically determined
from t(x),7-8 we need to analyse only one inhomogeneous slab
to obtain the solution for the 2-D structure. The coupling
Conclusion: The Taylor series approach to the inverse Laplace
transforms for rational and transcendental transfer functions
has been considered. The significant advantage is that each
transfer function is converted into a set of simultaneous linear
algebraic equations. This method is simple and very amenable
to computer programming. The results show that the agreement is excellent.
HUANG-YUAN CHUNG
YORK-YIH SUN*
Department of Mechanical Engineering
* Department of Electrical Engineering
National Cheng Kung University
Tainan, Taiwan, Republic of China
16th September 1986
References
1
CHEN, c. F., TSAY, Y. T., and wu, T. T.: 'Walsh operational matrices
for fractional calculus and their application to distributed systems',
J. Franklin Inst., 1977, 303, pp. 267-284
SHIEH, L. s., YATES, R. E., and NAVARRO, J. M.: 'Solving inverse
Laplace transform, linear and nonlinear state equations using
block-pulse functions', Comput. & Electr. Eng., 1979, 6, pp. 3-17
3 WANG, c. H.: 'Generalized block-pulse operational matrices and
their applications to operational calculus', Int. J. Control., 1982,
36, pp. 67-76
4 WANG, c. H.: 'On the generalization of block pulse operational
matrices for fractional and operational calculus', J. Franklin Inst.,
1983,315, pp. 91-102
5
CHOU, J. H., and HORNG, I. R.: 'On a functional approximation for
inversion of Laplace transforms via shifted Chebyshev series', Int.
J. Systems Sci., 1986,17, pp. 735-739
6 BELLMAN, R., KALABA, R., and LOCKETT, J.: 'Numerical inversion of
the Laplace transform' (American Elsevier, New York, 1966),
Chap. 2
ANALYSIS OF FUSED COUPLERS BY THE
EFFECTIVE-INDEX METHOD
y.
Indexing terms: Optical fibres, Optical couplers
Fused couplers of various cross-sections are analysed by the
effective-index method. Results show good agreement with
those given by an asymptotic analysis. It is also shown that a
stadium-shaped coupler which resembles the realistic one has
the polarisation beam-splitting property similar to that of a
rectangular one.
ELECTRONICS LETTERS 6th November 1986
Vol. 22
1319/11
Fig. 1 Fused coupler approximately modelled by a planar waveguide
with refractive-index profile (a) njjc) or (b) ny(y)
No. 23
1221
Das könnte Ihnen auch gefallen
- Data Transmission by Frequency-Division Multiplexing Using The Discrete Fourier TransformDokument7 SeitenData Transmission by Frequency-Division Multiplexing Using The Discrete Fourier TransformDa NyNoch keine Bewertungen
- Gpa8217 PDFDokument151 SeitenGpa8217 PDFdavid garduñoNoch keine Bewertungen
- Piston Vibrator BrochureDokument3 SeitenPiston Vibrator BrochuregemagdyNoch keine Bewertungen
- Protocol Lo Quam Tum 2Dokument3 SeitenProtocol Lo Quam Tum 2matteoriccicipolloni4606Noch keine Bewertungen
- Analysis and Applications of Laplace /fourier Transformations in Electric CircuitDokument7 SeitenAnalysis and Applications of Laplace /fourier Transformations in Electric CircuitSwasti RanjanNoch keine Bewertungen
- 21bma021-Review 2Dokument17 Seiten21bma021-Review 2ShanmathiNoch keine Bewertungen
- Analysis and Applications of Laplace/Fourier Transformations in Electric CircuitDokument8 SeitenAnalysis and Applications of Laplace/Fourier Transformations in Electric Circuitastro trumpNoch keine Bewertungen
- Laplace Transforms and Its ApplicationsDokument4 SeitenLaplace Transforms and Its ApplicationsAhmed S. El-MoghazyNoch keine Bewertungen
- Semiclassical Nonlinear Approach For Mesoscopic CircuitDokument4 SeitenSemiclassical Nonlinear Approach For Mesoscopic CircuitIJAERS JOURNALNoch keine Bewertungen
- Phase-Locked Loop For Grid-Connected Three-Phase Power Conversion SystemsDokument7 SeitenPhase-Locked Loop For Grid-Connected Three-Phase Power Conversion Systems181084aNoch keine Bewertungen
- CCP6 SlavaDokument10 SeitenCCP6 SlavaAndres PalchucanNoch keine Bewertungen
- Fifth&Sixth ProcedureDokument11 SeitenFifth&Sixth ProcedureAmir RabbaniNoch keine Bewertungen
- Mathematics Mini Pro 2 3Dokument8 SeitenMathematics Mini Pro 2 3Preethi PadmanabanNoch keine Bewertungen
- Mathematics Project: CSE1B - GR3 - 2018 - M201 - PROJDokument10 SeitenMathematics Project: CSE1B - GR3 - 2018 - M201 - PROJSudip BiswasNoch keine Bewertungen
- Jordanov NIMA.345.337 1994Dokument9 SeitenJordanov NIMA.345.337 1994leendert_hayen7107Noch keine Bewertungen
- Analysis of An Ac To DC Voltage Source Converter Using PWM With Phase and Amplitude ControlDokument8 SeitenAnalysis of An Ac To DC Voltage Source Converter Using PWM With Phase and Amplitude Controleubis_machado4370Noch keine Bewertungen
- Phase Domain Modelling of Frequency Dependent Transmission Lines by Means of An Arma ModelDokument11 SeitenPhase Domain Modelling of Frequency Dependent Transmission Lines by Means of An Arma ModelMadhusudhan SrinivasanNoch keine Bewertungen
- Characterization of High-Q Resonators For Microwave Filter ApplicationsDokument4 SeitenCharacterization of High-Q Resonators For Microwave Filter ApplicationshazardassNoch keine Bewertungen
- Mobile Communications: Homework 03Dokument4 SeitenMobile Communications: Homework 03Shahzeeb PkNoch keine Bewertungen
- J4 Distortion Correction CircuitsDokument8 SeitenJ4 Distortion Correction CircuitsАлексей ГрабкоNoch keine Bewertungen
- PLL For Grid-Connected Three Phase Power ConversisionDokument7 SeitenPLL For Grid-Connected Three Phase Power ConversisionNguyễn Quang SángNoch keine Bewertungen
- Advanced Iteration For A Magnetic Equivalent Circuit and Modeling A 3-Phase TransformerDokument6 SeitenAdvanced Iteration For A Magnetic Equivalent Circuit and Modeling A 3-Phase TransformerRadouan RadwanNoch keine Bewertungen
- Calculations of The Dispersive Characteristics of Microstrips by The Time-Domain Finite Difference MethodDokument5 SeitenCalculations of The Dispersive Characteristics of Microstrips by The Time-Domain Finite Difference MethodSudantha Jayalal PereraNoch keine Bewertungen
- Unified Frequency-Domain Analysis of Switched-Series-RC Passive Mixers and SamplersDokument14 SeitenUnified Frequency-Domain Analysis of Switched-Series-RC Passive Mixers and SamplersChandraKiranNoch keine Bewertungen
- Reduced-Complexity LLL Algorithm For Lattice-Reduction-Aided MIMO DetectionDokument5 SeitenReduced-Complexity LLL Algorithm For Lattice-Reduction-Aided MIMO DetectionRasool FarajiNoch keine Bewertungen
- Fast Transients Analysis of Non-Uniform Multiconductor Transmission Lines Excited by Incident FieldDokument6 SeitenFast Transients Analysis of Non-Uniform Multiconductor Transmission Lines Excited by Incident FieldItalo ChiarellaNoch keine Bewertungen
- Multicell Convertor - ObservatoriDokument6 SeitenMulticell Convertor - ObservatoriAndrei CocorNoch keine Bewertungen
- Small-Signal Model of A 5kW High-Output Voltage Capacitive-Loaded Series-Parallel Resonant DC-DC ConverterDokument7 SeitenSmall-Signal Model of A 5kW High-Output Voltage Capacitive-Loaded Series-Parallel Resonant DC-DC ConverterAshok KumarNoch keine Bewertungen
- Square-Root Forms of The Minimum Output Energy Detector and EstimatorDokument4 SeitenSquare-Root Forms of The Minimum Output Energy Detector and Estimatorsuchi87Noch keine Bewertungen
- Estimating The Number of Modes in Multimode Waveguide Propagation EnvironmentDokument4 SeitenEstimating The Number of Modes in Multimode Waveguide Propagation EnvironmentyomatotyNoch keine Bewertungen
- 21BMA021Dokument31 Seiten21BMA021ShanmathiNoch keine Bewertungen
- Laplace - Transform Anju BDokument25 SeitenLaplace - Transform Anju BJyothi upadhyayNoch keine Bewertungen
- Uo (W), Vo (W, UO (W) : T2 (W) Are Given by W 2, V 0 (W) w2Dokument4 SeitenUo (W), Vo (W, UO (W) : T2 (W) Are Given by W 2, V 0 (W) w2menguemengueNoch keine Bewertungen
- Spectrum AnalysisDokument35 SeitenSpectrum AnalysisdogueylerNoch keine Bewertungen
- Carrier Capture Cross Sections of Traps by DltsDokument7 SeitenCarrier Capture Cross Sections of Traps by Dltsdevendratiwari0Noch keine Bewertungen
- David M.Pozar-Input Impedance and Mutual Coupling of Rectangular Microstrip Antennas PDFDokument6 SeitenDavid M.Pozar-Input Impedance and Mutual Coupling of Rectangular Microstrip Antennas PDFBhargav Bikkani100% (1)
- (WSOLA) An Overlap-Add Technique Based On Waveform Similarity (WSOLA) For High-Quality Time-Scale Modifications of SpeechDokument4 Seiten(WSOLA) An Overlap-Add Technique Based On Waveform Similarity (WSOLA) For High-Quality Time-Scale Modifications of SpeechAniela MileaNoch keine Bewertungen
- clecocq,+JCAA Vol.11 No.3 1983 pp.047Dokument6 Seitenclecocq,+JCAA Vol.11 No.3 1983 pp.047zerjuniorNoch keine Bewertungen
- A Broad-Band TL Model For A Rectangular Microstrip AntennaDokument10 SeitenA Broad-Band TL Model For A Rectangular Microstrip AntennathgnguyenNoch keine Bewertungen
- Periodic Sequences With Optimal Properties For Channel Estimation and Fast Start-Up EqualizationDokument6 SeitenPeriodic Sequences With Optimal Properties For Channel Estimation and Fast Start-Up Equalizationbavar88Noch keine Bewertungen
- Classification of Power Quality Variations in Wind Power Systems-A Simulation ApproachDokument10 SeitenClassification of Power Quality Variations in Wind Power Systems-A Simulation ApproachraghvendraprasadNoch keine Bewertungen
- CX+JP: 1a +ko2 (4 I-4Dokument6 SeitenCX+JP: 1a +ko2 (4 I-4Raktim GuhaNoch keine Bewertungen
- The Appliance of Wavelet Transform in The Analysis of Seismic Structure Dynamic ReliabilityDokument8 SeitenThe Appliance of Wavelet Transform in The Analysis of Seismic Structure Dynamic ReliabilityprabhaakarNoch keine Bewertungen
- Hinsch 1988Dokument15 SeitenHinsch 1988Hussnain AliNoch keine Bewertungen
- 00001476Dokument8 Seiten00001476damaya1701Noch keine Bewertungen
- Redalyc: Sistema de Información CientíficaDokument9 SeitenRedalyc: Sistema de Información CientíficaJ Jesús Villanueva GarcíaNoch keine Bewertungen
- The Nonlinear Dynamics of Electrostatically-Actuated, Single-Walled Carbon Nanotube ResonatorsDokument12 SeitenThe Nonlinear Dynamics of Electrostatically-Actuated, Single-Walled Carbon Nanotube Resonatorsteju1996coolNoch keine Bewertungen
- Park TransformationDokument6 SeitenPark TransformationfirdousulnazirNoch keine Bewertungen
- Design HPklystronsDokument9 SeitenDesign HPklystronsrajarpitNoch keine Bewertungen
- 1043Dokument6 Seiten1043Eng-Sa'di Y. TamimiNoch keine Bewertungen
- Question Bank of Network Analysis and Synthesis UNIT-1 and UNIT-2Dokument9 SeitenQuestion Bank of Network Analysis and Synthesis UNIT-1 and UNIT-2PrakharGupta100% (1)
- App 4 LaplaceDokument6 SeitenApp 4 LaplaceRycille AlayanNoch keine Bewertungen
- Dyn Sim ModelDokument5 SeitenDyn Sim ModelJojo KawayNoch keine Bewertungen
- Discrete Cosine Transform PDFDokument4 SeitenDiscrete Cosine Transform PDFMohammad RofiiNoch keine Bewertungen
- Wavelet Transforms That Map Integers To IntegersDokument38 SeitenWavelet Transforms That Map Integers To IntegersPrasanna GaneshNoch keine Bewertungen
- Finite-Difference Time-Domain Model of Lasing Action in A Four-Level Two-Electron Atomic SystemDokument7 SeitenFinite-Difference Time-Domain Model of Lasing Action in A Four-Level Two-Electron Atomic System56mani78Noch keine Bewertungen
- Sensors: A Nonlinear Circuit Analysis Technique For Time-Variant Inductor SystemsDokument13 SeitenSensors: A Nonlinear Circuit Analysis Technique For Time-Variant Inductor SystemsEdi nbaNoch keine Bewertungen
- Energy Spectra of Few-Electron Quantum Dots: and A Matulis KDokument15 SeitenEnergy Spectra of Few-Electron Quantum Dots: and A Matulis KkatinasraibasNoch keine Bewertungen
- Laplace TransformDokument24 SeitenLaplace TransformChitransh SharmaNoch keine Bewertungen
- Spline and Spline Wavelet Methods with Applications to Signal and Image Processing: Volume III: Selected TopicsVon EverandSpline and Spline Wavelet Methods with Applications to Signal and Image Processing: Volume III: Selected TopicsNoch keine Bewertungen
- Power Electronics Applied to Industrial Systems and Transports, Volume 2: Power Converters and their ControlVon EverandPower Electronics Applied to Industrial Systems and Transports, Volume 2: Power Converters and their ControlBewertung: 5 von 5 Sternen5/5 (1)
- 1084 Geant Topology Mar 12Dokument1 Seite1084 Geant Topology Mar 12dchardwareNoch keine Bewertungen
- Beamer User GuideDokument245 SeitenBeamer User GuideColossus RhodesNoch keine Bewertungen
- Debugging OVS: Jus.n Pe0t April 14, 2011Dokument20 SeitenDebugging OVS: Jus.n Pe0t April 14, 2011Dimitris Alyfantis100% (1)
- Fitting Tool MatlabDokument1 SeiteFitting Tool MatlabGustavo MiottoNoch keine Bewertungen
- Math Mid Sem 1 Kiit PaperDokument1 SeiteMath Mid Sem 1 Kiit PapersellyNoch keine Bewertungen
- Advanced Composite Engineering Using MSC - Patran and FibersimDokument15 SeitenAdvanced Composite Engineering Using MSC - Patran and FibersimSandeep BandyopadhyayNoch keine Bewertungen
- PDE Multivariable FuncDokument16 SeitenPDE Multivariable Funcsaipavan iitpNoch keine Bewertungen
- Polynomial Problems From Recent Iranian Mathematical OlympiadsDokument15 SeitenPolynomial Problems From Recent Iranian Mathematical OlympiadsaayamNoch keine Bewertungen
- CBLM SketchingDokument18 SeitenCBLM SketchingGlenn F. Salandanan100% (3)
- The Harmonic Analysis of Tidal Model Time Series: M. G. G. Foreman and R. F. HenryDokument12 SeitenThe Harmonic Analysis of Tidal Model Time Series: M. G. G. Foreman and R. F. HenryANGGANoch keine Bewertungen
- 1997-01 Anal. Chem. 69, 3069-3075Dokument7 Seiten1997-01 Anal. Chem. 69, 3069-3075jfrojas60Noch keine Bewertungen
- Hydro Mechanical Systems in Simulink in SL Part 2 PDFDokument20 SeitenHydro Mechanical Systems in Simulink in SL Part 2 PDFAbdulhmeed MutalatNoch keine Bewertungen
- Peta Jaringan Layanan Angkutan UmumDokument1 SeitePeta Jaringan Layanan Angkutan UmumARFICONoch keine Bewertungen
- Pointers To ReviewDokument1 SeitePointers To ReviewRayven DenoyNoch keine Bewertungen
- Expense QuotasDokument3 SeitenExpense QuotasabhiNoch keine Bewertungen
- Determination of Temperature-Moisture Relationship by Linear Regression Models On Masonry and Floor, Kruja, AlbaniaDokument8 SeitenDetermination of Temperature-Moisture Relationship by Linear Regression Models On Masonry and Floor, Kruja, AlbaniaPhD. Arch. Klodjan XhexhiNoch keine Bewertungen
- Object Oriented Programming Question BankDokument4 SeitenObject Oriented Programming Question Bankvelmurugan_j100% (1)
- Polarization WavesDokument37 SeitenPolarization WavesNil TaiiayNoch keine Bewertungen
- Maths FTP NeevDokument10 SeitenMaths FTP NeevKaran SinghNoch keine Bewertungen
- Annuitization and The DARA HypothesisDokument29 SeitenAnnuitization and The DARA HypothesisTomás Valenzuela TormNoch keine Bewertungen
- Iitk Cse ResumeDokument3 SeitenIitk Cse ResumeAnimesh GhoshNoch keine Bewertungen
- Rock Mechanics Fundamentals: Foot) - What Is Its Specific Gravity?Dokument18 SeitenRock Mechanics Fundamentals: Foot) - What Is Its Specific Gravity?Ghulam Mohyuddin SohailNoch keine Bewertungen
- History of CompilersDokument18 SeitenHistory of CompilersMuhammad HamzaNoch keine Bewertungen
- Practical Research 2: Quarter 1 - Module 3Dokument51 SeitenPractical Research 2: Quarter 1 - Module 3bernadette domoloanNoch keine Bewertungen
- MATH 6342 - Advanced Enumeration: Definitions of A GroupDokument22 SeitenMATH 6342 - Advanced Enumeration: Definitions of A GroupjfeliperqNoch keine Bewertungen
- CSLABMANUALDokument99 SeitenCSLABMANUALGOKUL RNoch keine Bewertungen
- Asservissement PDFDokument5 SeitenAsservissement PDFMouad TalhaNoch keine Bewertungen
- Sessional-I Time TableDokument6 SeitenSessional-I Time TableRobin GautamNoch keine Bewertungen
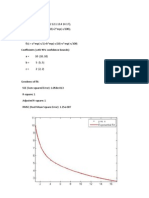
- Materials SB: 1+3.3log Log (N)Dokument10 SeitenMaterials SB: 1+3.3log Log (N)Thu NguyenNoch keine Bewertungen
- Stability of Concrete Gravity Dams Against Sliding Contact On The Bottom of Dam Foundation Using The Software ABAQUS and RS-DAMDokument15 SeitenStability of Concrete Gravity Dams Against Sliding Contact On The Bottom of Dam Foundation Using The Software ABAQUS and RS-DAMFoolad Gharb100% (1)
- 32 2H Nov 2021 QPDokument28 Seiten32 2H Nov 2021 QPXoticMemes okNoch keine Bewertungen