Ecuaciones Cap5

Captulo
ECUACIONES DIFERENCIALES DE
COEFICIENTES VARIABLES
5.1.
INTRODUCCIN
Una ecuacin diferencial de coeficientes variables presenta la forma geneeral:

[an (x)Dn + an1 (x)Dn1 + an2 (x)Dn2 + + a1 D + a0 ]y(x) = f (x)
De acuerdo con lo estudiado previamente, la solucin general de la ecuacin diferencial es de
la forma:
y(x) = C1 y1 (x) + C2 y2 (x) + + Cn yn (x) + yss (x)
En la expresin anterior se tiene que: {y1 , y2 , . . . , yn } es un conjunto fundamental de soluciones

de la homognea asociada mientras que yss es la solucin particular de la no homognea.
Para el caso de coeficientes constantes es relativamente simple determinar la solucin general
sin embargo, para coeficientes variables la situacin puede ser bastante complicada. Algunas
ecuaciones diferenciales tienen un tratamiento similar al de las de coeficientes constantes, tal
es el caso de la ecuacin diferencial de Euler. Para los otros casos se ver que el mtodo
adecuado de solucin mediante series de potencias.
5.2.
LA ECUACIN DIFERENCIAL DE EULER
La ecuacin diferencial de Euler1 de orden n presenta la forma general:
[an xn Dn + an1 xn1 Dn1 + an2 xn2 Dn2 + + a1 xD + a0 ]y(x) = f (x)

Leonhard Paul Euler (1707-1783): matemtico suizo, reconocido como uno de los ms grandes de
todos los tiempos. Con su prolija obra, hizo grandes aportes a las matemticas, clculo, teora de
grafos, mecnica, ptica y astronoma.
297
298 CAPTULO 5. ECUACIONES DIFERENCIALES DE COEFICIENTES VARIABLES

La homognea asociada admite soluciones de la forma y = x ; con C. As las cosas, al
reemplazar idnticamente en la homognea resulta una ecuacin polinmica conocida como
ecuacin caracterstica, as:
P () = an (1)(2) ((n1))+an1 (1)(2) ((n2))+ +a1 +a0 = 0
Resolviendo la ecuacin resulta un conjunto fundamental de soluciones de la homognea.
En cuanto a la solucin particular se aplica el mtodo de variacin de parmetros, previamente desarrollado.
Un mtodo alterno para encontrar el conjunto fundamental de soluciones de la homognea
consiste en realizar el cambio de variables: x = et . Se puede demostrar que la nueva ecuacin
diferencial resultante es una ecuacin de coeficientes constantes de la forma:
(an D(D 1)(D 2) (D (n 1)) + + a1 D + a0 ) y(t) = f (t)
La cual se soluciona con los mtodos estudiados en la seccin 2.3.
Para facilitar la comprensin del mtodo se iniciar con la ecuacin diferencial de Euler
de segundo orden.
5.2.1.
La ecuacin diferencial de Euler de segundo orden
La ecuacin diferencial de Euler de segundo orden presenta la forma general:

x2 y (x) + pxy (x) + qy(x) = x2 r(x)
con p, q constantes
El intervalo de validez de la solucin de la homognea es I = {x R / x = 0}. Para determinar

el conjunto fundamental de soluciones de la homognea se supone que admite soluciones de
la forma y = x , con lo que resulta la ecuacin caracterstica:
( 1) + p + q = 0
Al resolver la ecuacin se pueden presentar los siguientes casos:
1. Las races son reales y distintas: En este caso, el conjunto fundamental de soluciones
de la homognea es:
CF S = {x1 , x2 }
2. Las races son reales e iguales: En este caso, tenemos: 1 = 2 = y el CFS es:
CF S = {x , x ln(x)}
3. Las races son complejas conjugadas: En este caso, tenemos: 1 , 2 = j y
puede demostrarse que el CFS es:
CF S = {x sin ( ln(x)) , x cos ( ln(x))}
5.2. LA ECUACIN DIFERENCIAL DE EULER

Ejemplo: 5.1.
intervalo: x > 0
299
Encuentre la solucin general de la siguiente ecuacin diferencial en el

2x2 y (x) xy (x) + y(x) = 4x3
Solucin:
Primero que todo se escribe la ecuacin caracterstica, as:
2( 1) + 1 = 0
La ecuacin se puede escribir en forma factorizada, as:

(2 1)( 1) = 0
En consecuencia, un conjunto fundamental de soluciones de la homognea es:
CF S = {x, x }
Para determinar la solucin particular se escribe la ecuacin diferencial dada en su forma
normalizada, as:
1
1
y (x) y (x) + 2 y(x) = 2x
2x
2x
Usando el mtodo de variacin de parmetros, la solucin particular es de la forma: yss =
1 y 1 + 2 y 2 .
La aplicacin del mtodo conduce al siguiente sistema de ecuaciones:
x
x
0
1 1
=
1
2
2x
2 x
x
El Wronskiano del sistema es: W (x) =
2
Aplicando la regla de Cramer, se tiene:
1 = 2x x 1 = 4x 1 = 2x2
2
3
x
8 5
2 = 2x2 2 = 4x 2 2 = x 2
2
5
Entonces la solucin particular nos queda:
8 5 1
2
yss = 2x2 (x) x 2 (x 2 ) = x3
5
5
Por tanto, la solucin general de la ecuacin diferencial es:
2
y(x) = C1 x + C2 x + x3
5

Usando el mtodo alternativo, mediante del cambio de variables x = et , la ecuacin diferencial
nos queda:
[2D(D 1) D + 1]y(t) = 4e3t
Factorizando, tenemos: (2D 1)(D 1)y(t) = 4e3t .
De donde el conjunto fundamental de soluciones es:
CF S = {et , e 2 t }
Y la solucin particular, mediante el mtodo de operador inverso es:
yss (t) =
4e3t
2
= e3t
5(2)
5
Retornando a la variable original, la solucin general nos queda:

1
2
y(x) = C2 eln(x) + C2 e 2 ln(x) + e3 ln(x)
5
2 3
= C1 x + C2 x + x
5
5.2.2.
La ecuacin diferencial de Euler de tercer orden
La ecuacin diferencial de Euler de tercer orden presenta la forma general:

x3 y (x) + px2 y (x) + qxy (x) + sy(x) = x3 r(x)
con p, q, s constantes
La ecuacin caracterstica de la homognea asociada es:

( 1)( 2) + p( 1) + q + s = 0
Al resolver la ecuacin se pueden presentar los siguientes casos:
1. Las tres races son reales y diferentes: 1 , 2 , 3
En este caso, el conjunto fundamental de soluciones es:
CF S = {x1 , x2 , x3 }
2. Las tres races son reales, pero dos de ellas son iguales: 1 , 2 = 3 =
CF S = {x1 , x , x ln(x)}
3. Las tres races son reales e iguales: 1 = 2 = 3 =
CF S = {x , x ln(x), x ln2 (x)}
301
4. Dos races son complejas conjugadas y la otra es real: 1 , 2 , 3 = j

CF S = {x1 , x sin (ln(x)) , x cos (ln(x))}
Ejemplo: 5.2.
intervalo: x > 0.
Encuentre la solucin general de la siguiente ecuacin diferencial en el

x3 y (x) 2xy (x) + 4y(x) = x2
Solucin: Primero que todo se escribe la ecuacin caracterstica, as:
( 1)( 2) 2 + 4 = 0
La ecuacin se puede escribir en forma factorizada, as:

( + 1)( 2)2 = 0
En consecuencia, un conjunto fundamental de soluciones de la homognea es:
CF S = {x1 , x2 , x2 ln(x)}
Para determinar la solucin particular se escribe la ecuacin diferencial dada en su forma
normalizada, as:
2
4
y (x) 2 y (x) + 3 y(x) = x1
x
x
El mtodo de variacin de parmetros, conduce al siguiente sistema de ecuaciones:
1

x
x2
x2 ln(x)
1
0
x2 2x 2x ln(x) + x 2 = 0
2x3 2 2 ln(x) + 3
3
x1
El Wronskiano del sistema es W (x) = 9 . Aplicando la regla de Cramer, se tiene:
x3
3
3
92 = ln2 (x) ln(x)
2
93 = 3 ln(x)
91 = x2 91 =
92 = 3x1 ln(x) x1
93 = 3x1
La solucin particular es de la forma: yss = 1 y1 + 2 y2 + 3 y3 , por tanto:

3
x
3 2
1
2
9yss = x
x
ln (x) + ln(x) + x2 ln(x) (3 ln(x))
3
2
1
3
9yss = x2 x2 ln(x) + x2 ln2 (x)
3
2

Los dos primeros trminos son linealmente independientes con la homognea, por lo tanto la
solucin particular nos queda:
1
yss = x2 ln2 (x)
6
Y la solucin general es:
1
y(x) = C1 x1 + C2 x2 + C3 x2 ln(x) + x2 ln2 (x)
6
El procedimiento alternativo, mediante la sustitucin x = et , arroja la ecuacin diferencial:
(D + 1)(D 2)2 y(t) = e2t
De donde: CF S = {et , e2t , te2t }
Y la solucin particular es:
yss (t) =
e2t
te2t
t2 e2t
t2 e2t
=
=
=
(D + 1)(D 2)2 |D=2
3D2 6D|D=2
6(D 1)|D=2
6
Regresando a la variable original, la solucin general nos queda:

1
y(x) = C1 x1 + C2 x2 + C3 x2 ln(x) + x2 ln2 (x)
6
Ejemplo: 5.3.
Encuentre un conjunto fundamental de soluciones para cada una de las
siguientes ecuaciones diferenciales:
1. x2 y + xy y = 0
4. x2 y + 3xy + 2y = 0
3. x2 y xy + y = 0
5. x3 y + 3x2 y + xy 8y = 0
2. x2 y + xy + y = 0
Solucin:
1. La ecuacin caracterstica es:

( 1) + 1 = 0 ( 1)( + 1) = 0
El conjunto fundamental de soluciones es: CF S = {x, x1 }
( 1) + + 1 = 0 2 + 1 = 0
El conjunto fundamental de soluciones es: CF S = {sin(ln(x)), cos(ln(x))}
303

( 1) + 1 = 0 ( 1)2 = 0
El conjunto fundamental de soluciones es: CF S = {x, x ln(x)}
( 1) + 3 + 2 = 0 2 + 2 + 2 = 0
De donde: 1 , 2 = 1 j
El conjunto fundamental de soluciones es: CF S = {x1 sin(ln(x)), x1 cos(ln(x))}
( 1)( 2) + 3( 1) + 8 = 0 3 32 + 2 + 32 3 + 8 = 0
Simplificando, se tiene: 3 8 = ( 2)(2 + 2 + 4) = 0 . De donde:
1 = 2 2 , 3 = 1 j 3
El conjunto fundamental de soluciones es:
CF S = x2 , x1 sin
3 ln(x) , x1 cos
3 ln(x)
5.2.3.
Ecuaciones diferenciales reducibles a Euler
Algunas ecuaciones diferenciales se pueden reducir a ecuaciones de Euler mediante un cambio

de la variable dependiente, tal es el caso de la ecuacin diferencial:
(ax + b)2 y (x) + c(ax + b)y (x) + dy(x) = f (x)
con a, b, c, d constantes
Con base en lo estudiado previamente, el intervalo de validez de la solucin es:

I = {x R / ax + b = 0}
Para convertirla en una ecuacin diferencial de Euler se hace el cambio de variable: z = ax+b.
Con el cambio de la variable independiente se aplica la regla de la cadena para obtener:
dy dz
y (x) = ay (z)
dz dx
dy dz
y (x) =
y (x) = a2 y (z)
dz dx
y (x) =

As las cosas, la ecuacin diferencial para la nueva variable es:
zb
2 2
a z y (z) + aczy (z) + dy(z) = f

a
Ejemplo: 5.4.
Encuentre la solucin general de la ecuacin diferencial:

(2x + 1)2 y (x) + 2(2x + 1)y (x) 4y(x) = 2x + 2
Solucin: Al efectuar el cambio de variable z = 2x + 1 resulta la ecuacin diferencial:
4z 2 y (z) + 4zy (z 4y(z) = z + 1 z 2 y (z) + zy (z) y(z) =
z+1
4
La ecuacin caracterstica es:

( 1) + 1 = 0 2 1 = 0 ( 1)( + 1) = 0
El conjunto fundamental de soluciones de la homognea es:
CF S = {z, z 1 }
Para la solucin particular, hacemos el cambio de variable z = et con lo que la ecuacin nos
queda:
et + 1
(D2 1)z(t) =
4
La solucin particular, mediante operador inverso es:
yss (t) =
1 tet 1 1
tet 1
+
=
4 2
4 (1)
8
4
Retornando a la variable z, nos queda:

yss (z) =
z ln(z) 1
8
4
Y finalmente regresando a la variable original, la solucin general es:

y(x) = C1 (2x + 1) + C2 (2x + 1)1 +
(2x + 1) ln(2x + 1) 1
8
4
con x >
1
2
305
EJERCICIOS 5.1.
Encuentre un conjunto fundamental de soluciones para cada una de las siguientes ecuaciones
diferenciales:
1. x2 y + xy 4y = 0
6. x3 y + 3x2 y xy = 0
2. x2 y + xy + 4y = 0
7. x3 y + 2x2 y xy + y = 0
3. x2 y 3xy + 4y = 0
8. x3 y + 6x2 y + 5xy 5y = 0
4. x2 y + 3xy + 10y = 0
9. (2x 3)2 y + 8(2x 3)y + 8y = 0
5. x3 y + 3x2 y + xy = 0
10. (2x + 3)2 y + 10(2x + 3)y + 8y = 0
Resuelva cada uno de los siguientes problemas de valor inicial.

11. x2 y + xy 4y = x y(1) = 0 , y (1) = 0
12. x2 y 3xy + 4y = x2
13. x2 y + xy + 4y = x3
y(1) = 0 , y (1) = 0
y(1) = 0 , y (1) = 0
14. x3 y + 3x2 y + xy = 0 y(1) = 0 , y (1) = 1 , y (1) = 0

15. x3 y + 3x2 y xy = 0 y(1) = 0 , y (1) = 0 , y (1) = 1
Encuentre la solucin general para cada una de las siguientes ecuaciones diferenciales:
16. (2x 3)2 y + 8(2x 3)y + 8y = 2x
17. x2 y + 3xy + y = x2
18. x3 y + 2x2 y xy + y = x3
19. x3 y + 6x2 y + 5xy 5y = x2
20. x2 y + 3xy + y = x ln(x)
5.3.
SERIES DE POTENCIA
Consideremos una funcin de variable real y = f (x) tal que la funcin y todas sus derivadas
son continuas en un intervalo I R y sea x0 I. Una serie infinita de potencias, conocida
tambin como serie de Taylor, centrada en el punto x0 , es una expresin de la forma:
s(x) =
k=0
ck (x x0 ) =
k=0
ck (x x0 ) +
k=N +1
ck (x x0 )k
En su forma expandida es:

s(x) = c0 + c1 (x x0 ) + c2 (x x0 )2 + + cN (x x0 )N + cN +1 (x x0 )N +1 +
Concepto de convergencia
Se dice que una serie de potencias s(x) converge a una funcin f (x) en un entorno del punto
x0 si se verifica que f (x) s(x) . El intervalo de convergencia de la serie viene dado por:
I = {x R/|x x0 | < }
Donde es el es el radio de convergencia de la serie. La convergencia significa que la serie es
idntica a la funcin en cada punto del intervalo de convergencia. De acuerdo con lo anterior
podemos escribir:
f (x) = c0 + c1 (x x0 ) + c2 (x x0 )2 + + cN (x x0 )N +
k=N +1
ck (x x0 )k
En la expresin anterior, aparece un polinomio de grado N que se utiliza para aproximar la

funcin en el intervalo de convergencia. Intuitivamente, el polinomio de aproximacin es mejor
en la medida en que el grado del polinomio sea mayor. El resido de la serie viene dado por:
RN (x, x0 ) =
k=N +1
ck (x x0 )k
La convergencia implica que:

lm RN (x, x0 ) = 0
Clculo de los coeficientes de la serie

Dado que la serie es convergente a la funcin en cada punto del intervalo de convergencia,
todas las derivadas de la funcin coincidirn con todas las derivadas de la serie, es decir, se
5.3. SERIES DE POTENCIA
307
verifican las siguientes identidades:

f (x) = c0 + c1 (x x0 ) + c2 (x x0 )2 + c3 (x x0 )3 + c4 (x x0 )4 + c5 (x x0 )5 +
Df (x) = c1 (x x0 ) + 2c2 (x x0 ) + 3c3 (x x0 )2 + 4c4 (x x0 )3 + 5c5 (x x0 )4 +
D2 f (x) = 2c2 + 2 3c3 (x x0 ) + 3 4c4 (x x0 )2 + 4 5c5 (x x0 )3 +
D3 f (x) = 2 3c3 + 2 3 4c4 (x x0 ) + 3 4 5c5 (x x0 )2 +
D4 f (x) = 2 3 4 + 2 3 4 5c5 (x x0 ) +
..
.
Evaluando en el punto x = x0 , resulta:
D2 f (x0 )
c0 = f (x0 ) c1 = Df (x0 ) c2 =
2!
D3 f (x0 )
c3 =
3!
...
Dn f (x0 )
cn =
n!
Criterio de la razn
El criterio de la razn, que es el cociente entre dos trminos consecutivos de la serie y permite
determinar el intervalo de convergencia de una serie, as:
cn+1 (x x0 )n+1
<1
lm
n
cn (x x0 )n
En la expresin anterior se supone que la diferencia, en grado, entre dos trminos consecutivos
es la unidad. Lo anterior no es necesariamente cierto en todos los casos.
Series de Maclaurin
Cuando el punto alrededor del cual se hace el desarrollo de la serie es x0 = 0 , la serie de
Taylor recibe el nombre de serie de Maclaurin.
A continuacin se muestra una tabla con las series asociadas a las funciones de mayor inters
en ingeniera. Se indica, en cada caso, el intervalo de convergencia.
Funcin exponencial
ex =
xk
k=0
k!
=1+x+
x2 x3
+
+
2!
3!
; I=R
Funcin seno
sin(x) =
(1)k x2k+1
k=0
(2k + 1)!
=x
x3 x5 x7
+
+
3!
5!
7!
; I=R

Funcin coseno
cos(x) =
(1)k x2k
k=0
Funcin
(2k)!
x2 x4 x6
=1
+
+
2!
4!
6!
; I=R
1
1x
1
=
xk = 1 + x + x2 + x3 + x4 +
1 x k=0
; I = {x R/|x| < 1}
Funcin ln(1 x)
xk+1
x2 x3 x4 x5
ln(1 x) =
=x+
+
+
+
+
k
+
1
2
3
4
5
k=0
; I = {x R/|x| < 1}
Es posible determinar la serie de Maclaurin de cualquier funcin mediante el clculo directo

de los coeficientes o haciendo uso de las series de funciones conocidas.
Ejemplo: 5.5.
Escriba la serie de Maclaurin para la funcin f (x) = ln(2x + 3) , indicando el intervalo de convergencia.
Solucin:
La funcin dada se puede escribir en la forma:
2x
2x
2x
f (x) = ln(2x + 3) = ln 3 1 +
= ln(3) + ln 1 +
= ln(3) + ln 1
3
3
3
Haciendo uso de la serie de la funcin ln(1 x), resulta:

ln(2x + 3) = ln(3) +
k=0
2x k+1
3
k+1
2x
4x2
8x3
16x4
32x4
= ln(3)
+
+
3
2 32 3 33 4 34 5 35
El intervalo de convergencia viene dado por:

2x
3
I = x R/ < 1 = x R/|x| <

3
2
Solucin de ejemplo 5.5 con Mxima: Para expandir la funcin ln(2x + 3) en polinomios de Taylor de grado 8, entorno al punto x0 = 0, mediante Mxima, se ejecuta el
comando:
309
(%i1) taylor(log(2*x+3),x,0,8);
Cuyo resultado es:
( %o1) log (3) +
2 x 2 x2 8 x3 4 x4 32 x5 32 x6 128 x7 32 x8
+ ...
3
9
81
81
1215 2187 15309 6561
Si deseamos encontrar la expresin en series de potencias, ejecutamos el comando:

(%i2) powerseries(log(2*x+3), x, 0);
Obteniendo:
3i1 (2)i xi+1
( %o2) 2
i+1
i=0
Solucin de ejemplo 5.5 con Matlab: Usando MATLAB es comando es el mismo,

pero los argumentos de entrada difieren. En este caso se define el nmero de trminos de la
serie deseados y el punto entorno al cual se desarrollar. La secuencia de comandos a ejecutar
es:
>> syms x ; pretty(taylor(log(2*x+3),9,0))
8
32 x
128 x
32 x
32 x
4 x
8 x
2 x
2 x
- ----- + ------ - ----- + ----- - ---- + ---- - ---- + --- + log(3)
6561
15309
2187
1215
81
81
9
3
Multiplicacin de series de potencias

Se desea encontrar la serie de Maclaurin del producto de dos funciones conocidas las series
individuales, as:
n
f (x) =
an x
g(x) =
bm x m
m=0
k=0
El producto se obtiene de multiplicar cada trmino de la primera serie por la segunda, as:
f (x)g(x) = a0
bm x +a1 x
m=0
bm x +a2 x
m=0
bm x +a3 x
m=0
m=0
La expresin anterior se puede escribir en la forma:

f (x)g(x) =
m=0
a0 b m x +
m=0
a1 b m x
m+1
a2 b m x
m+2
m=0
bm x + +an x
a3 b m x
m+3
m=0
+ +
bm x m
m=0
an bm xm+n
m=0
Un anlisis detallado de la expresin anterior nos permite decir que la serie correspondiente
al producto es de la forma:
2
f (x)g(x) = c0 + c1 x + c2 x + c3 x + =
i=0
ci xi

Donde:
c 0 = a0 b 0
c 1 = a0 b 1 + a1 b 0
c2 = a0 b2 + a1 b1 + a2 b0
..
.
ci =
aj bij
j=0
El intervalo de convergencia del producto es la interseccin de los intervalos de convergencia

individuales.
Ejemplo: 5.6.
Encuentre la serie de Maclaurin de la funcin f (x) = ex x sin(2x), indicando el intervalo de convergencia.
Solucin: Partimos de las series de cada uno de los factores, as:

x
e =
sin(2x) =
(x)k
k=0
k=0
k!
=1x+
x2 x3
+
2!
3!
; I=R
(1)k (2x)2k+1
(2x)3 (2x)5 (2x)7
= 2x
+
+
(2k + 1)!
3!
5!
7!
Con base en lo presentado, resulta:

1
19
ex sin(2x) = 2x 2x2 x3 + x4 x5 + ; I = R
3
60
Solucin de ejemplo 5.6 con Mxima:
(%i1) taylor(exp(-x)*sin(2*x),x,0,8);
( %o1) 2 x 2 x2
x3
19 x5 11 x6 139 x7
x8
+ x4
+ ...
3
60
180
2520
120
Solucin de ejemplo 5.6 con Matlab:

>> syms x; pretty(taylor(exp(-x)*sin(2*x),9,0))
8
x
139 x
11 x
19 x
4
x
2
- --- + ------ - ----- - ----- + x - -- - 2 x + 2 x
120
2520
180
60
3
; I=R
311
Divisin de series de potencias

Para dividir dos series de potencias se usa el algoritmo de divisin de polinomios. El proceso
puede resultar bastante tedioso, pero no hay otra alternativa. En cuanto al intervalo de convergencia, se debe garantizar que el denominador no se anule en el mismo.
Ejemplo: 5.7.
Encuentre la serie de Maclaurin de la funcin f (x) = tan(x), indicando
el intervalo de convergencia.
Solucin:
Puesto que la tangente es el cociente entre la funcin seno y la funcin coseno,
se concluye que el intervalo de convergencia de la serie de Maclaurin es:
I = x R/|x| <
2
El cociente indicado es:
(1)k x2k+1
x3 x5 x7
x
+
k=0
(2k + 1)!
3!
5!
7!
tan(x) =
=
(1)k x2k
x2 x4 x6
1
+
k=0
2!
4!
6!
(2k)!
Efectuando la divisin, resulta:
1
2
17 7
tan(x) = x + x3 + x5 +
x +
3
15
315
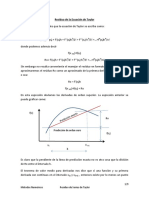
En la figura 5.1 se muestra la funcin tan(x) en linea slida junto con los polinomios de aproximacin de grados n = 3, 5 y 7 en lineas punteadas. Puede verse que la convergencia para
n = 7 es perfecta en el intervalo: [1, 1].
Solucin de ejemplo 5.7 con Mxima: Calculamos el polinomio de Taylor de grado 15, entorno de x0 = 0:
(%i1) taylor(tan(x),x,0,15);
( %i1) x +
x3 2 x5 17 x7 62 x9 1382 x11 21844 x13

929569 x15
+
+
+
+
+
+
+ ...
3
15
315
2835
155925
6081075
638512875
Si queremos encontrar la expresin en series de potencias:

(%i2) powerseries(tan(x),x,0);
Cuyo resultado es:
(1)i1 (22 i 1) 22 i bern (2 i) x2 i1
( %o2)
(2 i)!
i=0
n =7
n =5
3
2
n =3
-1
-1
-2
-3
-4
Figura 5.1: Grfica de tan(x) y polinomios de aproximacin de grados n = 3, 5 y 7
Donde bern son los nmeros de Bernoulli2 .

Solucin de ejemplo 5.7 con Matlab:
>> syms x; pretty(taylor(tan(x),16,0))
15
13
11
9
7
5
3
929569 x
21844 x
1382 x
62 x
17 x
2 x
x
---------- + --------- + -------- + ----- + ----- + ---- + -- + x
638512875
6081075
155925
2835
315
15
3
EJERCICIOS 5.2.
Escriba la serie de Maclaurin para cada una de las siguientes funciones, indicando el intervalo
de convergencia:
1. f (x) =
sin(x)
1+x
2. f (x) = sinh(x)
2
Remtase al Apndice A.3.
cos(2x)
(1 + x)2
1+x
4. f (x) = ln
1x
3. f (x) =
5.4. SOLUCIN POR SERIES DE ECUACIONES DIFERENCIALES

ln(3x + 5)
1 x2
9. f (x) = x + 1
5. f (x) = x cot(x)
8. f (x) =
6. f (x) = tan1 (x)

7. f (x) =
5.4.
313
cosh(x)
1 x2
10. f (x) =
1
x+1
SOLUCIN POR SERIES DE ECUACIONES DIFERENCIALES
Consideremos una ecuacin diferencial lineal de segundo orden, as:

y (x) + p(x)y (x) + q(x)y(x) = r(x)
De acuerdo con lo estudiado previamente, si {y1 , y2 } es un conjunto fundamental de soluciones
de la homognea y yss es una solucin particular de la no homognea, la solucin general de
la ecuacin diferencial viene dada por:
y(x) = C1 y1 + C2 y2 + yss
5.4.1.
Teora general de solucin por series
Se considerar, en primera instancia, la ecuacin diferencial homognea, es decir, la ecuacin

diferencial:
y (x) + p(x)y (x) + q(x)y(x) = 0
Las siguientes definiciones nos orientarn para encontrar un conjunto fundamental de soluciones de la ecuacin diferencial.
Funcin analtica
Se dice f (x) es una funcin analtica o funcin regular en un entorno del punto x0 si
admite un desarrollo en series de potencias en dicho entorno. Una condicin necesaria
para que la funcin sea analtica es que el siguiente lmite exista:
lm {f (x)}
xx0
Las funciones elementales tratadas previamente: exponencial,

seno y coseno, son fun
ciones analticas en los reales. La funcin: f (x) = x no es analtica en un entorno de
x0 = 0 ya que sus diferentes derivadas no estn definidas en dicho punto.
Cuando la funcin es el cociente de dos funciones analticas, la analiticidad de la funcin est sujeta a la existencia del lmite previamente establecido. Esto significa que una
condicin suficiente, para que el cociente de dos funciones analticas en un intervalo sea

analtico, es que el lmite exista.
sin(x)
La funcin f (x) =
, por ejemplo, es analtica en x0 = 0 ya que:
x
sin(x)
=1
x0
x
lm
Punto ordinario
Se dice que x0 es un punto ordinario de la ecuacin diferencial homognea si las funciones
p(x) y q(x) son analticas entorno de dicho punto.
Punto singular
Se dice que x0 es un punto singular de la ecuacin diferencial homognea si una de las
funciones p(x) o q(x) no es analtica en un entorno de dicho punto.
En general los puntos singulares o singularidades de la ecuacin diferencial son nmeros
complejos y se representan mediante cruces en dicho plano.
Ejemplo: 5.8.
Determine las singularidades de las siguientes ecuaciones diferenciales:
1. (x x3 )y + sin(x)y + xy = 0
2. (8 + x3 )y + xy + 2y = 0
3. (x2 + 2x + 10)y + xy + 2y = 0
Solucin:
1. A partir de la ecuacin se tiene que:

p(x) =
sin(x)
x(1 x2 )
q(x) =
1
1 x2
Por simple inspeccin, las singularidades son x = 1.

2. En este caso, se tiene:
p(x) =
(x +
x
2x + 4)
2)(x2
q(x) =
(x +
2
2x + 4)
2)(x2
Por simple inspeccin se

tiene que: x = 2 es una singularidad y las otras dos singularidades, son: x = 1 j 3 .
3. El estudiante puede mostrar que las singularidades son: x = 1 j3
5.4.2.
315
Soluciones entorno a un punto ordinario
Consideremos la ecuacin diferencial homognea:

y (x) + p(x)y (x) + q(x)y(x) = 0
Si x0 es un punto ordinario de la ecuacin diferencial y la singularidad ms cercana a dicho
punto es xs , la ecuacin admite soluciones de la forma de Taylor en un intervalo I, dado por:
I = {x R/|x x0 | < |xs x0 |}
As las cosas, la serie: y(x) =
k=0
ck (x x0 )k es solucin de la ecuacin diferencial y, en
consecuencia, la debe satisfacer idnticamente. Expandiendo la serie, se tiene:
y(x) = c0 + c1 (x x0 ) + c2 (x x0 )2 + + cN (x x0 )N + cN +1 (x x0 )N +1 +
De acuerdo con lo estudiado previamente, los coeficientes de la serie se determinan de la
siguiente manera:
c0 = y(x0 ) c1 = y (x0 ) c2 =
y (x0 )
2!
...
cn =
y n (x0 )
n!
Puesto que y(x0 ) y y (x0 ) son las condiciones iniciales de la ecuacin diferencial, es decir, son
conocidas, entonces las otras constantes se pueden obtener a partir de ellas, de la siguiente
manera:
y (x0 )
Para hallar la constante: c2 =
, se despeja y (x) de la ecuacin diferencial:
2!
y (x) = q(x)y(x) p(x)y (x)
Y se evala en x0 , resultando:
c2 =
Para la constante c3 =
q(x0 )y(x0 ) p(x0 )y (x0 )

q(x0 )c0 p(x0 )c1
=
2!
2!
y (x0 )
, se deriva la ecuacin (5.1) resultando:
3!
y (x) = q (x)y(x) [q(x) + p(x)]y (x) p(x)y (x)

Evaluando en x0 , nos queda:
[q (x0 ) + p(x0 )]c0 + [q(x0 ) p(x0 ) + p2 (x0 )]c1
c3 =
3!
(5.1)

Procediendo de manera iterativa se determinan las dems constantes. Todas las constantes
dependen de las constantes arbitrarias c0 , c1 . Lo anterior nos permite escribir la solucin de
la ecuacin diferencial en la forma:
q(x0 )c0 p(x0 )c1

y(x) =c0 + c1 (x x0 ) +
(x x0 )2 +
2!
[q (x0 ) + p(x0 )]c0 + [q(x0 ) p(x0 ) + p2 (x0 )]c1

(x x0 )3 +
3!
2
La expresin anterior se puede escribir en la forma: y(x) = c0 y1 (x) + c1 y2 (x), con:
q(x0 )
[q (x0 ) + p(x0 )]
2
y1 (x) = 1 +
(x x0 ) +
(x x0 )3 +
2!
3!
p(x0 )
[q(x0 ) p(x0 ) + p2 (x0 )]
2
y2 (x) = (x x0 ) +
(x x0 ) +
(x x0 )3 +
2!
3!
Para que las dos funciones descritas conformen un conjunto fundamental de soluciones de la
homognea se requiere que el Wronskiano sea diferente de cero en cada punto del intervalo de
convergencia.
Recordando la frmula de Abel (2.2), se tiene: W (x) = Ke p(x)dx .

Puesto que p(x) es analtica en el intervalo de convergencia, el Wronskiano es diferente de cero en el mismo, con lo cual: {y1 , y2 } es un conjunto fundamental de soluciones de la homognea.
El procedimiento descrito para resolver la ecuacin diferencial homognea puede hacerse extensivo a la ecuacin diferencial no homognea, slo que el intervalo de convergencia debe
tener en cuenta a la funcin r(x).
Ejemplo: 5.9.
Encuentre un conjunto fundamental de soluciones, entorno de x0 = 0
para la ecuacin diferencial de Airy, indicando el intervalo de convergencia.
y (x) xy(x) = 0
Solucin: De acuerdo con lo planteado previamente, x0 = 0 es un punto ordinario de la
ecuacin diferencial y dado que no hay singularidades, la ecuacin admite dos soluciones de
la forma de Maclaurin en el dominio de los reales, as:
y(x) = c0 + c1 x + c2 x2 + c3 x3 + c4 x4 + + cN xN + cN +1 xN +1 +
317
Tal como acabamos de ver, c0 , c1 son constantes arbitrarias. Por otro lado, se tiene:
y (x) = xy(x) y (0) = 0 c2 = 0
c0
D3 y(x) = xy (x) + y(x) D3 y(0) = y(0) = c0 c3 =
3!
2c1
4
D y(x) = xy (x) + 2y (x) D y(0) = 2y (0) = 2c1 c4 =

4!
D5 y(x) = xD3 y(x) + 3y (x) D5 y(0) = 0 c5 = 0
4c0
D6 y(x) = xD4 y(x) + 4D3 y(x) D6 y(0) = 4D3 y(0) = 4c0 c6 =
6!
10c1
De manera similar puede mostrarse que c7 =
. Con base en los resultados, se tiene:
7!
1
2
4
10
y(x) = c0 + c1 x + c0 x3 + c1 x4 + c0 x6 + c1 x7 +
3!
4!
6!
7!
El resultado puede escribirse en la forma:
1 3 4 6
2 4 10 7
y(x) = c0 1 + x + x + + c1 x + x + x +
3!
6!
4!
7!
Ejemplo: 5.10. Encuentre la solucin general en un entorno de x0 = 0 de la siguiente
ecuacin diferencial, indicando el intervalo de validez.
(x2 + 4)y (x) + y(x) = x
Solucin:
Las singularidades de la ecuacin diferencial son: x = j2.
En consecuencia, el intervalo de convergencia de la solucin es:

I = {x R/|x| < 2}
Para resolver la ecuacin diferencial se parte de las constantes arbitrarias c0 , c1 y se procede

como en el ejemplo 5.9, as:
x y(x)
y(0)
c0
2
D
y(0)
=
=
c2
x2 + 4
4
4
4 x2 (x2 + 4)y (x) 2xy(x)
4 4c1
D3 y(x) =
D3 y(0) =
c3
2
2
(x + 4)
16
4xDy(x) 3D2 y(x)
3D2 y(0)
3c0
4
D4 y(x) =
D
y(0)
=
=
c4
x2 + 4
4
42 2!
6xD4 y(x) 7D3 y(x)
7D4 y(0)
5
D5 y(x) =
D
y(0)
=
c5
x2 + 4
4
..
.
D2 y(x) =
c0
4 2!
1 c1
=
4 3!
3c0
= 2
4 2!4!
7(c1 1)
= 2
4 3!5!
=

Como puede notarse, es bastante laborioso el proceso de derivacin sucesiva en este caso.
Despus de hacer el trabajo, resulta:
c
1 c1
3c0
7(c1 1)
0
2
3
4
y(x) = c0 + c1 x +
x +
x +
x +
x5 +
4 2!
4 3!
42 2!4!
42 3!5!
Reorganizando trminos, podemos ver que adems de las dos soluciones homogneas tenemos
la solucin particular. La solucin general es: y(x) = c0 y1 (x) + c1 y2 (x) + yss (x).
Donde:
x2
3x4
+ 2

4 2! 4 2!4!
x3
7x4
y2 (x) = x
+ 2

4 3! 4 3!5!
x3
7x5
yss (x) =
2
+
4 3! 4 3!5!
y1 (x) = 1
Ejemplo: 5.11. Encuentre un conjunto fundamental de soluciones, entorno de x0 = 2

para la siguiente ecuacin diferencial, indicando el intervalo de convergencia.
xy (x) y (x) y(x) = 0
Solucin: De acuerdo con lo planteado previamente, x0 = 2 es un punto ordinario de la
ecuacin diferencial, mientras que x0 = 0 es un punto singular de la misma.

Por tanto, la ecuacin admite dos soluciones de la forma de Taylor:
y(x) = c0 + c1 (x 2) + c2 (x 2)2 + c3 (x 2)3 + + cN (x 2)N + cN +1 (x 2)N +1 +

En el intervalo: I = {x R/|x 2| < 2}
Para facilitar el trabajo se hace el cambio de variable z = x 2 y se efecta el desarrollo
entorno de z0 = 0. Para la nueva variable, la ecuacin diferencial es:
(z + 2)y (z) y (z) y(z) = 0
Realizando el procedimiento, tenemos:
y(z) + y (z)
y(0) + y (0)
D2 y(0) =
z+2
2
y
(z)
c1
D3 y(z) =
D3 y(0) =
z+2
2
3
y
(z)
D
y(z)
y
(0)
D
y(0)
D4 y(z) =
D4 y(0) =
z+2
2
2
4
D y(z) 2D y(z)
c0
D5 y(z) =
D5 y(0) =
z+2
4
D2 y(z) =
c0 + c1
2 2!
c1
c3 =
2 3!
c1
c4 =
4 4!
c0
c5 =
4 5!
c2 =

Con base en los resultados, la solucin es:
c0 + c1
c1 3
c1 4
y(z) = c0 + c1 z +
z2 +
z +
z +
2 2!
2 3!
4 4!
z2
z5
z2
z3
y(z) = c0 1 +
+
+ + c1 z +
+
+
2 2! 4 5!
2 2! 2 3!
319
c0 5
z +
4 5!
z4
+
4 4!
Retornando a la variable original, resulta:
(x 2)2 (x 2)5
(x 2)2 (x 2)3 (x 2)4
y(x) = c0 1 +
+
+ +c1 (x 2) +
+
+
+
2 2!
4 5!
2 2!
2 3!
4 4!
5.4.3.
Mtodo de los coeficientes indeterminados
De acuerdo con lo estudiado hasta el momento, es claro que puede resultar muy engorroso el
clculo de los coeficientes de la serie por el mtodo de la derivacin sucesiva de la ecuacin
diferencial. El mtodo de los coeficientes indeterminados nos permite obviar ese inconveniente,
veamos:
Dada la ecuacin diferencial:
a2 (x)y (x) + a1 (x)y (x) + a0 (x)y(x) = f (x)
Se parte de suponer que la ecuacin diferencial admite una solucin de la forma de Maclaurin,
es decir, se resolver la ecuacin en un entorno de x0 = 0 , as:
y(x) =
ck xk
k=0
Las dos primeras derivadas de la funcin vienen dadas por:
y (x) =
kck x
k1
y (x) =
k=0
k=0
ck (k 1)xk2
Sustituyendo idnticamente en la ecuacin diferencial, resulta:

a2 (x)
k=0
ck (k 1)x
k2
+ a1 (x)
k=0
kck x
k1
+ a0 (x)
k=0
ck xk f (x)
Es bueno precisar que los coeficientes de la ecuacin diferencial y el trmino independiente admiten desarrollos en series de Maclaurin. Preferentemente nos ocuparemos de resolver
ecuaciones diferenciales cuyos coeficientes sean polinmicos, lo cual facilita el procedimiento.

Ejemplo: 5.12. Resuelva la ecuacin diferencial del ejemplo 5.9 por el mtodo de los
coeficientes indeterminados.
Solucin:
La ecuacin diferencial a resolver es la ecuacin diferencial de Airy:
y (x) xy(x) = 0
Al sustituir las series correspondientes a la funcin y su segunda derivada, resulta la identidad:
k=0
k(k 1)ck xk2
k=0
ck xk+1 0
Para poder agrupar las sumatorias en una sola, es necesario que sus ndices coincidan, para
que los trminos agrupados correspondan a las mismas potencias de la variable. Para esto,
hacemos los cambios de variables n = k 2 enla primera sumatoria y n = k + 1 en la segunda.
As las cosas, la identidad anterior queda en la forma:
n=2
(n + 2)(n + 1)cn+2 xn
n=1
cn1 xn 0
Desarrollando los tres primeros trminos de la primera sumatoria, resulta:

0 c0 x2 + 0 c1 x1 + 2c2 x0 +
n=0
[(n + 2)(n + 1)cn+2 cn1 ]xn 0
A partir de la identidad se concluye que todos los coeficientes deben ser iguales a cero, esto
es:
0 c0 = 0 0 c1 = 0 2c2 = 0 (n + 2)(n + 1)cn+2 cn1 = 0 para n = 1, 2, 3, . . .
De la expresin anterior se sigue que: c0 = 0, c1 = 0 y c2 = 0. Por otro lado, resulta una
ecuacin que permite hallar los dems coeficientes, conocida como ecuacin de recurrencia y
viene dada por:
cn1
cn+2 =
para n = 1, 2, 3, . . .
(n + 1)(n + 2)
A partir de la ecuacin de recurrencia, se obtienen los coeficientes:
c3 =
c0
23
c4 =
c1
34
c5 =
c2
= 0,
45
La solucin se puede escribir como:
y(x) = c0 + c1 x +
c6 =
c3
c0
=
,
56
2356
c7 =
c4
c1
=
,
67
3467
c0 3 2c1 4 4c0 6 2 5c1 7

x +
x +
x +
x +
3!
4!
6!
7!
c8 = 0,
321
Finalmente, la solucin queda en la forma:

y(x) = c0
1
4
1 + x3 + x6 +
3!
6!
+ c1
2
25 7
x + x4 +
x +
4!
7!
Los productos sucesivos 147 y 258 se pueden escribir ms compactamente mediante

la notacin Pochhammer3 as:
3
1
+
3
= (3 + 1) (3 + 4) (3 + 3k 2) con = 0, 1
Con esto, la solucin encontrada se puede escribir como:

1
x3k
3 k (3k)!
2 4 2 5 7 2 5 8 10
2
x3k+1
k
y2 = x + x +
x +
x + =
3
4!
7!
10!
3 k (3k + 1)!
k=0
1
14 6 147 9
y1 = 1 + x3 +
x +
x + =
3k
3!
6!
9!
k=0
Las soluciones de la ecuacin de Airy son conocidas como funciones de Airy y se suelen
escribirse como combinaciones lineales de las funciones y1 y y2 , as:
Ai(x) = k1 y1 k2 y2
Bi(x) =
3 [k1 y1 + k2 y2 ]
Donde:
k1 = Ai(0) =
Bi(0)
= 32/3 ( 23 ) 0.35503
k2 = Ai (0) = Bi3(0) = 31/3 ( 13 ) 0.25882

De tal forma que la solucin de la ecuacin diferencial es:
y(x) = c1 Ai(x) + c2 Bi(x)
La figura 5.2 ilustra las grficas de las funciones de Airy Ai(x) en lnea continua y Bi(x) en
lnea punteada.
3
Remtase al apndice A.2
Figura 5.2: Funciones de Airy Ai(x), Bi(x)
Encuentre la solucin general de la ecuacin diferencial:
Ejemplo: 5.13.
y (x) + xy(x) = sin(x) , entorno de x0 = 0
Solucin:
Al aplicar el mtodo, resulta:
k=0
k(k 1)ck x
k2
k=0
ck x
k+1
(1)k x2k+1
k=0
(2k + 1)!
Realizando los cambios de variables: n = k 2 en la primera sumatoria y n = k + 1 en la

segunda, nos queda:
(n + 2)(n + 1)cn+2 x +
n=2
n=1
cn1 xn x
x3 x5 x7
+
+
3!
5!
7!
Desarrollando los tres primeros trminos de la primera sumatoria, resulta:

0 c0 x
+ 0 c1 x
+ 2c2 x +
n=1
[(n + 1)(n + 2)cn+2 + cn1 ]xn x
x3 x5 x7
+
+
3!
5!
7!
A partir de la identidad se concluye que los tres primeros coeficientes deben ser iguales a cero,
esto es:
0 c0 = 0 0 c1 = 0 2c2 = 0
323
Por otro lado se tiene que:

1 c0
1 c0
=
23
3!
c1
2c1
=
=
34
4!
1
1
=
=
4 5 3!
5!
c3
1 c0
4(1 c0 )
=
=
=
56
2356
6!
1
2c1
1
2 5c1
= +
= +
7! 6 7 4!
7!
7!
c5
6
=
=
78
8!
1
4 7(1 c0 )
= +
9!
9!
n = 1 2 3c3 + c0 = 1 c3 =
n = 2 3 4c4 + c1 = 0 c4
n = 3 4 5c5 + c2 =
1
c5
3!
n = 4 5 6c6 + c3 = 0 c6
n = 5 6 7c7 + c4 =
1
c7
5!
n = 6 7 8c8 + c5 = 0 c8
n = 7 8 9c9 + c6 =
1
c9
7!
..
.
La solucin general nos queda:
1 c0
2c1 4
1 5 4(1 c0 ) 6
1
2 5c1
3
y(x) = c0 + c1 x +
x
x x +
x +
+
x7
3!
4!
5!
6!
7!
7!
6 8
1
4 7(1 c0 )
+ x +
+
x9 +
8!
9!
9!
Reorganizando trminos, nos queda:
x3 4x6 4 7x9
y(x) = c0 1
+
3!
6!
9!
2x4 2 5x7
+ c1 x
+
+
4!
7!
3
x
x5 4x6 x7 6x8 27x9
+
+
+
+
3!
5!
6!
7!
8!
9!
Como puede verse, la solucin obtenida son las funciones de Airy ms una serie de trminos
independientes que corresponden a la solucin particular, esto es:
y(x) = c1 Ai(x) + c2 Bi (x) +
x3 x5 4x6 x7 6x8 27x9
+
+
+
3!
5!
6!
7!
8!
9!

Ejemplo: 5.14.
de x0 = 0.
Encuentre la solucin general de la siguiente ecuacin diferencial entorno
Solucin: La ecuacin se puede expresar en la forma:
y (x) + ex y(x) = x2
y (x) +
xk
k=0
k!
y(x) = x2
Puesto que admite soluciones de la forma de Maclaurin, se tiene:
x2 x3
k2
k(k 1)ck x
+ 1+x+
+
+
ck xk x2
2!
3!
k=0
k=0
Expandiendo algunos trminos, resulta:
k=0
k(k 1)ck x
k2
ck x +
k=0
ck x
k+1
k=0
1
1
+
ck xk+2 +
ck xk+3 +
2! k=0
3! k=0
1
ck xk+N + x2
N ! k=0
Se realiza el cambio de variable: n = k 2 en la primera sumatoria, n = k en la segunda,

n = k + 1 en la tercera y as sucesivamente. Con los cambios resulta:
1
1
(n + 2)(n + 1)cn+2 x +
cn x +
cn1 x +
cn2 xn +
cn3 xn +
2!
3!
n=2
n=0
n=1
n=2
n=1
n
1
cnN xn + x2
N ! n=1
Desarrollando trmino a trmino e igualando los coeficientes, se obtiene:

n = 2 0 c0 = 0 c0 =
0
n = 1 0 c1 = 0 c1 =
0
c0
2
(c0 + c1 )
=
3!
1 c1
2(1 c1 )
=
=
34
4!
3c0 2c1
=
5!
9c0 2c1 + 2
=
6!
n = 0 2c2 + c0 = 0 c2 =
n = 1 3 2C3 + c1 + c0 = 0 c3
c0
= 1 c4
2!
c1 c0
n = 3 4 5c5 + c3 + c2 + +
= 0 c5
2! 3!
c2 c1 c0
n = 4 5 6c6 + c4 + c3 + + +
= 0 c6
2! 3! 4!
..
.
n = 2 3 4c4 + c2 + c1 +
325
La solucin de la ecuacin diferencial es:
x x3 3x5 32 x6
x3 2x4 2x5 2x6
y(x) =c0 1
+
+
+ + c1 x
+
+
2
3!
5!
6
3!
4!
5!
6!
4
2x
2x6
+
+
4!
6!
Otra forma de resolver la ecuacin diferencial es la siguiente:
y=
cn x
e =
n=0
xn
n=0
n!
e y =
bn x
con bn =
n=0
cnk
k=0
k!
As las cosas, al sustituir idnticamente en la ecuacin diferencial resulta:
n=2
n(n 1)cn x
n2
n=0
bn x n x 2
Haciendo los cambios correspondientes en los ndices de las sumatorias, se tiene:
(m + 2)(m + 1)cm+2 x +
m=0
m=0
bm x m x 2
Se obtiene, la ecuacin de recurrencia:
cm+2
m c
mk
k=0 k!
=
(m + 2)(m + 1)
para m = 2
Particularmente, para m = 2, resulta:

1 (c2 + c1 +
1 b2
c4 =
=2
34
4!
c0
)
2
El estudiante puede verificar que al desarollar los trminos se llega al mismo resultado.
EJERCICIOS 5.3.
Resuelva, por los dos mtodos, cada una de las siguientes ecuaciones diferenciales en un
entorno del punto dado, indicando el intervalo de convergencia.
1. y (x) xy (x) y(x) = x , x0 = 0.
3. xy (x) xy (x) y(x) = x , x0 = 1.
2. (1x)y (x)xy (x)y(x) = 0 , x0 = 0.
4. y (x) sin(x)y(x) = x , x0 = 0.

5. (1 x2 )y (x) 2xy (x) + 2y(x) = 0 ,
x0 = 0.
9. ex y (x) y(x) = x , x0 = 0.
6. y (x) ex y(x) = sin(x) , x0 = 0.
7. (x + 2)y (x) xy(x) = x , x0 = 0.
5.5.
8. xy (x) y (x) + xy(x) = 0 , x0 = 1.
10. y (x) + xy (x) y(x) = x2 , x0 = 0.
SOLUCIONES ENTORNO DE UN PUNTO SINGULAR
Consideremos la ecuacin diferencial lineal homognea de segundo orden:

y (x) + p(x)y (x) + q(x)y(x) = 0
Supongamos que: x0 R es un punto singular de la ecuacin diferencial, esto es, al menos una
de las funciones p(x), q(x) no es analtica en un entorno de dicho punto. Lo anterior significa
que la ecuacin diferencial no admite, necesariamente, soluciones de la forma de Taylor.
5.5.1.
Puntos singulares regulares
Se dice que x0 es un punto singular regular de la ecuacin diferencial si las siguientes funciones
modificadas son analticas en un entorno de dicho punto:
P (x) = (x x0 )p(x) Q(x) = (x x0 )2 q(x)
Lo anterior significa que dichas funciones tienen desarrollos en series de Taylor en algn
entorno de dicho punto, as:
P (x) = (x x0 )p(x) = a0 + a1 (x x0 ) + a2 (x x0 )2 + a3 (x x0 )3 +
Q(x) = (x x0 )2 q(x) = b0 + b1 (x x0 ) + b2 (x x0 )2 + b3 (x x0 )3 +
La ecuacin diferencial modificada es:
(x x0 )2 y (x) + (x x0 )P (x)y (x) + Q(x)y(x) = 0
Como puede verse, la ecuacin modificada es muy similar a la ecuacin diferencial de Euler.
Precisamente, debido a la analoga, George Frobenius4 propuso como solucin de la ecuacin
diferencial una serie de la forma:
y(x) = (x x0 )
4
k=0
ck (x x0 ) =
k=0
ck (x x0 )k+
(5.2)
Ferdinand Georg Frobenius (1849-1917): Matemtico alemn reconocido por sus aportes a la teora
de las ecuaciones diferenciales y a la teora de grupos.
5.5. SOLUCIONES ENTORNO DE UN PUNTO SINGULAR
327
La serie es una modificacin de la serie de Taylor en la que es un nmero complejo.

Al sustituir en la ecuacin diferencial, se obtiene:
k=0
(k + )(k + 1)ck (x x0 )
k+
+ P (x)
k=0
(k + )ck (x x0 )
k+
+ Q(x)
La identidad anterior se puede escribir en la forma:
k=0
k=0
ck (x x0 )k+ 0
[(k + )(k + 1) + P (x)(k + ) + Q(x)] ck (x x0 )k+ 0
La expresin anterior se verifica para todo valor de k . Particularmente se cumple cuando

toma el valor cero, as:
[( 1) + P (x) + Q(x)] c0 (x x0 ) 0
Puesto que el primer coeficiente debe ser diferente de cero, para obtener soluciones diferentes
de la trivial y dado que: P (x) y Q(x) son analticas en x0 , resulta una ecuacin conocida como
ecuacin indicial que tiene dos soluciones para . La ecuacin indicial es:
( 1) + P (x0 ) + Q(x0 ) = 0
(5.3)
Realmente, la ecuacin indicial debe escribirse en la forma:
2
( 1) + lm (x x0 )p(x) + lm (x x0 ) q(x) = 0
xx0
xx0
A partir de la ecuacin indicial resultan dos soluciones para la ecuacin diferencial, as:
y1 =
k=0
ak (x x0 )k+1
y2 =
k=0
bk (x x0 )k+2
Las dos soluciones obtenidas no forman, necesariamente, un conjunto fundamental de soluciones. Evidentemente, s las races de la ecuacin indicial son iguales slo se obtiene una
solucin. La otra solucin puede obtenerse por reduccin de orden, aunque se estudiar un
mtodo alternativo ms adelante.
En cuanto al intervalo de convergencia de la solucin, si x1 es la singularidad ms prxima a
x0 , el intervalo de convergencia es:
{x R/x0 < x < |x x1 |}
Para simplificar el anlisis se supondr que x0 = 0, es decir, las dos soluciones de la ecuacin
diferencial estn dadas por:
y1 =
k=0
ak x
k+1
y2 =
k=0
bk xk+2

En este caso, La ecuacin diferencial, se puede escribir en la forma:
x2 y (x) + xP (x)y (x) + Q(x)y(x) = 0
Donde:
P (0)x2 P (0)x3
+
+
2!
3!
Q (0)x2 Q (0)x3
Q(x) =Q(0) + Q (0)x +
+
+
2!
3!
P (x) =P (0) + P (0)x +
Puesto que se suponen soluciones de la forma: y =
ck xk+ , al sustituir la solucin en la
k=0
ecuacin diferencial, resulta la identidad:
P (0) 2 P (0) 3
k+
ck (k + )(k + 1)x
+ P (0) + P (0)x +
x +
x +
ck (k + )xk+ +
2!
3!
k=0
k=0
Q (0) 2 Q (0) 3
Q(0) + Q (0)x +
x +
x +
ck xk+ 0
2!
3!
k=0
Sacando factor comn x y desarrollando la expresin anterior, se tiene:
k=0
[(k + )(k + 1) + P (0)(k + ) + Q(0)]ck xk +
P (0) + Q (0)
2!
k=0
ck xk+2 + +
[(k + )P (0) + Q (0)]ck xk+1 +
k=0
P (0) + Qm (0)
m!
k=0
ck xk+m 0
Se hace el cambio de variable n = k en la primera sumatoria, n = k + 1 en la segunda,

n = k + 2 en la tercera, n = k + m en la m-sima y as sucesivamente. Con esto, resulta:
n=0
[(n + )(n + 1) + P (0)(k + ) + Q(0)]cn x +
P (0) + Q (0)
n=2
2!
cn2 xn + +
n=1
[(n 1 + )P (0) + Q (0)]cn1 xn +
P (0) + Qm (0)
n=m
m!
cnm xn 0
Expandiendo los trminos de las sumatorias, tenemos:
[( 1) + P (0) + Q(0)]c0 x0
+ [[( + 1) + P (0)( + 1) + Q(0)]c1 + [P (0) + Q (0)]c0 ] x

P (0) + Q (0)
+ [( + 2)( + 1) + P (0)( + 2) + Q(0)]c2 + [P (0)( + 1) + Q (0)]c1 +

c0 x2
2!
+ 0
329
Puesto que todos los coeficientes deben ser iguales a cero, se obtienen las siguientes ecuaciones:
[( 1) + P (0) + Q(0)]c0 = 0
[[( + 1) + P (0)( + 1) + Q(0)]c1 + [P (0) + Q (0)]c0 ] = 0

P (0) + Q (0)
[( + 2)( + 1) + P (0)( + 2) + Q(0)]c2 + [P (0)( + 1) + Q (0)]c1 +

c0 = 0
2!
..
. ... = 0
Si definimos las funciones:
f () = ( 1) + P (0) + Q(0)
gm () =
P m (0) + Qm (0)
m!
El conjunto de ecuaciones anteriores se puede escribir como:

f () = [( 1) + P (0) + Q(0)]c0 = 0
..
.
n
f ( + n)cn +
gm ( + n m)cnm = 0
m=1
Con lo que resulta la ecuacin de recurrencia:
cn =
m=1
gm ( + n m)cnm
f ( + n)
para n = 1, 2, 3, 4 . . .
(5.4)
Puesto que estamos interesados en soluciones no triviales, se impone la condicin co = 0, con

lo que resulta la ecuacin indicial:
f () = ( 1) + P (0) + Q(0) = 0
5.5.2.
(5.5)
Naturaleza de las races de la ecuacin indicial
Las soluciones de la ecuacin indicial (5.5) son:
P (0) + 1 (P (0) 1)2 4Q(0)

1 , 2 =
2
A partir de la ecuacin de recurrencia dada en (5.4) se tiene:
cn =
m=1
gm ( + n m)cnm
( + n)( + n 1) + P (0)( + n) + Q(0)
para n = 1, 2, 3, 4 . . .
(5.6)

Reemplazando la ecuacin indicial (5.5) en la ecuacin anterior, nos queda:
cn =
m=1
gm ( + n m)cnm
n(n + P (0) 1 + 2)
para n = 1, 2, 3, 4 . . .
Para los valores obtenidos en la (5.6), resulta la ecuacin de recurrencia:
gm ( + n m)cnm
cn =
n(n (P (0) 1)2 4Q(0) )
m=1
para n = 1, 2, 3, 4 . . .
(5.7)
Cuando las races de la ecuacin indicial son iguales, el discriminante se anula y la ecuacin
de recurrencia, nos queda:
n
gm ( + n m)cnm
m=1
cn =
para n = 1, 2, 3, 4 . . .
n2
Y expandiendo los coeficientes, resulta:
c1 = g1 ()c0
[g1 ( + 1)c1 + g2 ()c0 ]
g2 () + g1 ( + 1)g1 ()
c2 =
=
c0
22
4
..
.
Lo cual indica que slo se encuentra una solucin.
Supongamos
ahora
que
las
races
son
diferentes
y
que
el
discriminante
(P (0) 1)2 4Q(0) =
a no es un nmero natural. La ecuacin de recurrencia queda:

n
gm ( + n m)cnm
m=1
cn =
para n = 1, 2, 3, 4 . . .
n(n a )
Como puede verse, el denominador nunca se anula y, en consecuencia, resultan dos soluciones,
una por cada valor de .
Supongamos ahora que las races son diferentes pero difieren en un entero, es decir, la raz
cuadrada del discriminante es un nmero natural: N , as:
n
gm ( + n m)cnm
m=1
cn =
para n = 1, 2, 3, 4 . . .
n(n N )
Como puede verse, el denominador no se anula para la mayor de las races, es decir, la mayor
de las races proporciona una solucin. Por otro lado, el denominador se anula para n = N ,
caso en el cual se presentan dos posibilidades, as:
331
1. El numerador es diferente de cero.

En este caso, el coeficiente: cN no se puede determinar.
2. El numerador es cero.
En este caso, el coeficiente: cN es una constante arbitraria y, por tanto, resultan dos
soluciones para la ecuacin diferencial. Los dems coeficientes se obtienen a partir de la
ecuacin de recurrencia que resulte de aplicar el mtodo.
5.5.3.
Mtodo de Frobenius para resolver la ecuacin diferencial
Dada la ecuacin diferencial: a2 (x)y (x) + a1 (x)y (x) + a0 (x)y(x) = 0, si x0 = 0 es un punto

singular regular de la ecuacin diferencial y x1 es la singularidad ms prxima a x0 = 0, la
ecuacin diferencial admite, al menos, una solucin de la forma:
y=
k=0
ck xk+ = x [c0 + c1 x + c2 x2 + c3 x3 + c4 x4 + ]
Las soluciones son vlidas en el intervalo: I = {x R/0 < x < x1 } .

Para encontrar la solucin se procede conforme a lo presentado previamente.
Ejemplo: 5.15. Encuentre la solucin general de la siguiente ecuacin diferencial, indicando el intervalo de convergencia:
xy (x) + y (x) + xy(x) = 0
Solucin:
Por simple inspeccin, se tiene que p(x) =
1
x
y q(x) = 1 De donde: xp(x) = 1 y
x q(x) = x .
Con base en lo estudiado, el punto x0 = 0 es la nica singularidad de la ecuacin diferencial
y, adems, es un punto singular regular. En consecuencia, la ecuacin diferencial admite, al
menos, una solucin de la forma de Frobenius en el intervalo x > 0.
Para resolver la ecuacin diferencial partimos de las series correspondientes a la funcin y sus
dos primeras derivadas, as:
2
y=
ck xk+
k=0
y =
(k + )ck xk+1
k=0
y =
k=0
(k + )(k + 1)ck xk+2
k=0
(k + )(k + 1)ck x
k+2
(k + )ck x
k+1
k=0
k=0
ck xk++1 0
Sacando x de factor comn y agrupando las dos primeras sumatorias, se tiene:
x
[(k + )(k + 1) + (k + )]ck xk1 +
ck xk+1 0
k=0
k=0

Puesto que x = 0, la expresin anterior se puede escribir en la forma:
(k + ) ck x
k1
k=0
k=0
ck xk+1 0
Realizando los cambios de variable: n = k 1 en la primera sumatoria y n = k + 1 en la

segunda, nos queda:
2
n
(n + 1 + ) cn+1 x +
cn1 xn 0
n=1
n=1
Al desarrollar los dos primeros trminos de la primera sumatoria resulta:

2
c0 x
+ ( + 1) c1 x +
n=1
(n + 1 + )2 cn+1 + cn1 xn 0
De la expresin anterior se concluye que, si c0 = 0, la ecuacin indicial es: 2 = 0 y por tanto

las races son iguales a cero. Como puede verse c1 = 0.
La ecuacin de recurrencia, para el valor hallado de viene dada por:
cn1
cn+1 =
n = 1, 2, 3, 4, . . .
(n + 1)2
Asignando valores, resulta:
c0
c2
c0
c0
c0 = 0 c1 = 0 c2 = 2 c3 = 0 c4 = 2 = 2 2 c5 = 0 c6 = 2 2 2
2
4
2 4
2 4 6
Se obtiene una solucin de la forma:
x2
x4
x6
y(x) = c0 1 2 + 2 2 2 2 2 +
2
2 4
2 4 6
La otra solucin se puede determinar por el mtodo de reduccin de orden estudiado en el

captulo 2.4.1. Remtase al ejemplo 5.17.
Ejemplo: 5.16. Encuentre la solucin general de la siguiente ecuacin diferencial, indicando el intervalo de convergencia:
xy (x) + 2y (x) + xy(x) = 0
Solucin: Por simple inspeccin, se tiene que Con base en lo estudiado, el punto: x0 = 0
es la nica singularidad de la ecuacin diferencial y, adems, es un punto singular regular.

En consecuencia, la ecuacin diferencial admite, al menos, una solucin de la forma de Frobenius en el intervalo x > 0 . Para resolver la ecuacin diferencial partimos de las series
correspondientes a la funcin y sus dos primeras derivadas, as:
y=
k=0
ck x
k+
y =
k=0
(k + )ck x
k+1
y =
k=0
(k + )(k + 1)ck xk+2
333
k=0
(k + )(k + 1)ck x
k+1
+2
(k + )ck x
k+1
k=0
k=0
ck xk++1 0
Sacando x de factor comn y agrupando las dos primeras sumatorias, se tiene:
x
[(k + )(k + 1) + 2(k + )]ck xk1 +
ck xk+1 0
k=0
k=0
Puesto que x = 0, la expresin anterior se puede escribir en la forma:
(k + )(k + + 1)ck x
k1
k=0
k=0
ck xk+1 0
Realizando los cambios de variable: n = k 1 en la primera sumatoria y n = k + 1 en la

segunda, nos queda:
(n + 1 + )(n + + 2)cn+1 x +
n=1
n=1
cn1 xn 0
Al desarrollar los dos primeros trminos de la primera sumatoria resulta:

( + 1)c0 x
+ ( + 1)( + 2)c1 x +
n=1
[(n + 1 + )(n + 2 + )cn+1 + cn+1 ] xn 0
De la expresin anterior se concluye que, si c0 = 0, la ecuacin indicial es: ( + 1) = 0 y

por tanto las races son 1 = 0, 2 = 1. Como puede verse, cuando se toma la menor de las
races resulta que c1 = 0. La ecuacin de recurrencia, para el valor tomado de viene dada
por:
cn1
cn+1 =
n = 1, 2, 3, 4, . . .
n(n + 1)
Asignando valores, resulta:
c0
c1
c2
c0
c3
c1
c4
c0
c0 = 0 c1 = 0 c2 =
c3 =
c4 =
=
c5 =
=
c6 =
=
2
3!
34
4!
45
5!
56
6!
Se obtiene la solucin:

x2 x4 x6
x3 x5 x7
1
y(x) = x
c0 1
+
+ + c1 x
+
+
2!
4!
6!
3!
5!
7!
Con base en lo estudiado previamente en la seccin 5.3, se tiene:
cos(x)
sin(x)
+ c1
para x > 0
x
x
Como puede verse, la menor de las races de la ecuacin indicial nos proporciona dos soluciones
linealmente independientes.
y(x) = c0
5.5.4.
Mtodo para calcular la segunda solucin
Como se sugiri en la seccin 5.5.2, la determinacin de la segunda solucin de la ecuacin

diferencial depende de la naturaleza de las races de la ecuacin indicial. nicamente en los
casos en que las races son iguales o difieren en un entero el proceso de solucin conlleva a
una sola solucin y1 de la ecuacin diferencial. Veamos el procedimiento en cada caso:
1. Las races de la ecuacin indicial son iguales
En este caso, la otra raz se determina mediante el mtodo de reduccin orden, estudiado
en el captulo 2.4.1, as:
p(x)dx
e
y2 = y1
dx
y12
La aplicacin de la frmula conlleva un trabajo operativo bastante arduo, sobre todo
cuando la solucin conocida no es una funcin elemental.
A continuacin se muestra una alternativa que facilita los clculos.
Se parte de la ecuacin diferencial modificada, as:
x2 y (x) + xP (x)y (x) + Q(x)y(x) = 0
2 2
x D + xP (x)D + Q(x) y(x) = 0
Usando la notacin L(x, D) = x2 D2 + xP (x)D + Q(x) , la ecuacin diferencial se escribe

como: L(x, D)y(x) = 0.
Se supone una solucin de la forma: y(, x) =

ck ()xk+ y se sustituye idnticamente
en la ecuacin diferencial, obtenindose:
k=0
[( 1) + P (0) + Q(0)] c0 x + [[( + 1) + P (0)( + 1) + Q(0)]c1 + [P (0) + Q (0)] x+1
+ [( + 2)( + 1) + P (0)( + 2) + Q(0)]c2 + [P (0)( + 1) + Q (0)]c1

P (0) + Q (0)
+
c0 x+2 + 0
2!
f ()c0 x + [f ( + 1)c1 + g1 ()c0 ]x+1 + [f ( + 2)c2 + g1 ( + 1)c1 + g2 ()c0 ]x+2 +
+ f ( + n)cn +
gm ( + n m)cnm xn+ 0
m=1
Cuando las races de la ecuacin caracterstica son iguales, es decir 1 = 2 , se tiene

que f () = ( 1 )2 . En este caso todos los coeficientes de la combinacin lineal son
iguales a cero, excepto el primero, con lo cual la ecuacin diferencial modificada es:
2 2
x D + xP (x)D + Q(x) y(, x) = ( 1 )2 c0 x
335
Equivalentemente se tiene:L(x, D)y(, x) = ( 1 )2 c0 x .

Derivando parcialmente con respecto a , se tiene:
( 1 )2 c0 x
L(x, D)y(, x)
=
= ( 1 )2 ln(x) + 2( 1 ) c0 x
Ya que el operador L(x, D) no depende de , la expresin anterior es equivalente a la

siguiente:
y(, x)
L(x, D)
= ( 1 )2 ln(x) + 2( 1 ) c0 x
Evaluando en el valor conocido para , resulta:
y(, x)
L(x, D)
=0
=1
Lo anterior significa que la funcin:
cial.
Ya que y(, x) =
y(, x)
tambin es solucin de la ecuacin diferen
ck ()xk+ , derivando con respecto a resulta:
k=0
y(, x)
=
ck ()xk+ + y(, x) ln(x)
n=1
En conclusin, las dos soluciones de la ecuacin diferencial son:

y1 = y(, x) y2 =
y(1 , x)
En la prctica se supone que la segunda solucin es de la forma:

y2 =
bk xk+ + Cy1 ln(x)
k=0
Donde la constante C se escoge convenientemente.

2. Las races de la ecuacin indicial difieren en un entero
Cuando las races difieren en un entero, la mayor de ellas proporciona una solucin.
La otra solucin puede determinarse por un procedimiento similar al desarrollado previamente.
Omitiendo los detalles, la segunda solucin presenta la forma:
y2 =
k=0
bk xk+2 + Cy1 ln(x)

Encuentre una segunda solucin para la ecuacin diferencial del ejemplo
Ejemplo: 5.17.
5.15.
Solucin:
La ecuacin diferencial a resolver es: xy (x) + y (x) + xy(x) = 0 .
Tal como se procedi en el ejemplo 5.15, una de las soluciones hallada con = 0 es:
x2
x4
x6
+
+
22 22 42 22 42 62
En cuanto a la segunda solucin, se deriva dos veces y se sustituye en la ecuacin diferencial,
as:
1
y2 =
bk xk + Cy1 ln(x) y2 =
kbk xk1 + C
+ y1 ln(x)
x
k=0
k=0
y1 2y1
k2
y2 =
k(k 1)bk x
+C 2 +
+ y1 ln(x)
x
x
k=0
y1 = 1
Al sustituir en la ecuacin diferencial, resulta:
y1 2y1
C 2+
+ y1 ln(x) +
k(k 1)bk xk2 +
x
x
k=0
k1
C
+ y1 ln(x) +
kbk x
+
bk xk + Cy1 ln(x) 0
x
k=0
k=0
C
ln(x)[xy1
y1
+ xy1 ] +
2Cy1
k=0
k(k 1)bk x
k1
kbk x
k=0
k1
k=0
bk xk+1 0
Ahora, dado que y1 es solucin de la ecuacin diferencial, el primer trmino de la expresin

anterior es idnticamente nulo. Con esto y simplificando la expresin, nos queda:
k=0
k bk x
k1
k=0
bk xk+1 2Cy1
Haciendo el cambio de variables n = k 1 en la primera sumatoria y n = k + 1 en la segunda,

se tiene:
x2
x4
x6
2
n
n
(n + 1) bn+1 x +
cn1 x 2C
1 2 + 2 2 2 2 2 +
dx
2
2 4
2 4 6
n=1
n=1
Al expandir los dos primeros trminos de la primera sumatoria, se tiene:
2x
4x3
6x5
1
0
2
n
0.b0 x + b1 x +
(n + 1) [bn+1 + bn1 ]x 2C 0 2 + 2 2 2 2 2 +
2
2 4
2 4 6
n=2
337
De lo anterior se sigue que b0 = 0 y b1 = 0. Por otro lado, si se hace 2C = 1, resulta la

identidad:
2x
4x3
6x5
2
n
(n + 1) [bn+1 + bn1 ]x
2 2 + 2 2 2
2
2
2 4
2 4 6
n=2
Asignamos valores a n para determinar los coeficientes bk de la solucin:
1
b2
2
n = 2 9b3 + b1 = 0 b3
1
1
1 1 b0
n = 3 16b4 + b2 = b4 =
b4
16
256 16 8
4
n = 4 b5
1 b0
8
4
=0
1
b0
=
+
256 64
=0
1
b0
n = 5 b6 =
27650 2304
n = 1 4b2 + b0 =
En consecuencia, la segunda solucin es:
1
1 b0
1
b0
1
b0
2
4
y2 = y1 ln(x) + b0 +
x +
+
x
+
x6 +
2
8
4
256 64
27650 2304
1
x2
x4
x6
x2 x4
x6
y1 ln(x) +
+
+
+ + b0 1
+
+
2
8
256 27650
4
64 2304
Puesto que la serie que acompaa a la constante b0 es la primera solucin, entonces, la segunda
solucin es:
1
x2
x4
x6
y2 = y1 ln(x) +
+
+
+
2
8
256 27650
Ejemplo: 5.18. Encuentre la solucin general de la siguiente ecuacin diferencial entorno
de x0 = 0, indicando el intervalo de convergencia.
x x2 y (x) 2y (x) + 6y(x) = 0
2
6
Solucin:
Por simple inspeccin, se tiene que p(x) = x(1 x) y q(x) = x(1 x) . Se
sigue que:
2
6
Q(x) = x2 q(x) =
1x
1x
En consecuencia x0 = 0 es un punto singular regular y la singularidad ms cercana es x1 = 1.
Por tanto, el intervalo de validez es:
P (x) = xp(x) =
I = {x R/0 < x < 1}

Para resolver la ecuacin diferencial se suponen soluciones de la forma de Frobenius, as:
y=
ck xk+
k=0
Siguiendo el procedimiento usual, resulta:
k=0
(k + )(k + 1)ck x
k+1
k=0
(k + )(k + 1)ck x
k+1
2
+6
k=0
k=0
(k + )ck xk+1
ck xk+ 0
Agrupando en dos sumatorias y sacando x como factor comn, resulta:
k=0
(k + )(k + 3)ck x
k1
k=0
[(k + )(k + 1) 6]ck xk 0
k=0
(k + )(k + 3)ck x
k1
k=0
(k + 3)(k + + 2)ck xk 0
Haciendo los cambios de variable adecuados, se tiene:
n=1
(n + + 1)(n + 2)cn+1 x
n=0
(n + 3)(n + + 2)cn xn 0
De donde la ecuacin indicial es: f () = ( 3) = 0.

Y la ecuacin de recurrencia es:
cn+1 =
(n + 3)(n + + 2)
cn
(n + + 1)(n + 2)
n = 0, 1, 2, 3, . . .
De acuerdo con lo estudiado, la mayor de las races = 3 proporciona una solucin, as:
y1 =
k=0
ck xk+3 = x3 c0 + c1 x + c2 x2 + c3 x3 +
Donde c0 = 0 y la ecuacin de recurrencia queda: cn+1 =
n(n + 5)
cn
(n + 4)(n + 1)
De donde se obtiene: c1 = 0, c2 = 0, c3 = 0, . . . , cn = 0.
Por lo tanto una solucin de la ecuacn diferencial es: y1 = x3 .
n = 0, 1, 2, . . .
339
Para la menor de las races = 0, la ecuacin de recurrencia nos queda:

cn+1 =
(n 3(n + 2)
cn
(n + 1)(n 2)
n = 0, 1, 2, . . .
Como puede verse, la constante c3 no se puede determinar y por tanto es necesario hallar la
segunda solucin por otro mtodo.
a.) Por reduccin de orden:
y2 = x
2
dx
x(1x)
x6
dx =
e2 ln(x)2 ln(1x)
dx = x3
x6
x4 (1
1
dx
x)2
Efectuando las operaciones, tenemos:

4
3
2
1
4
1
3
y2 =x
+
+
+
+
dx
x x2 x3 x4 1 x (1 x)2
3
1
1
1
3
=x 4 ln(x) 4 ln(1 x) 2 3 +
x x
3x
1x
3
1
x
=4x3 ln(x) 4x3 ln(1 x) x +
3 1x
k+1
x
1
3
3
3
=4x ln(x) 4x
x +x
xk
k
+
1
3
k=0
k=0
Desarrollando los trminos de las series de potencia y simplificando, obtenemos:

y2 = 4x3 ln(x)
1
7x6
9x8
x 3x2 + x3 + 5x4 + 3x5 +
+ 2x7 +
+
3
3
5
La cual se puede escribir como:
1
x 3x2 x3 5x4 3x5 7x6 x7 9x8
3
y2 = 4 x ln(x)

+
+
+
+
+
+
+
12 4
4
4
4
4
12
2
20
b.) Suponiendo solucin de la forma y2 =
bk xk+2 + Cy1 ln(x) :
k=0
Para = 0 se tiene:
y2 =
bk xk + Cx3 ln(x)
k=0
Tomando las dos primeras derivadas, resulta:

y2
k=0
kbk x
k1
+ C[x + 3x ln(x)]
y2
k=0
k(k 1)bk xk2 + C[5x + 6x ln(x)]

Al sustituir en la ecuacin diferencial: (x x2 ) y (x) 2y (x) + 6y(x) = 0, nos queda:
2
C[5x + 6x ln(x)] +
k(k 1)bk x
k=0
2C[x2 + 3x2 ln(x)] 2
k1
C[5x + 6x ln(x)]
kbk xk1 + 6Cx3 ln(x) + 6
k=0
k=0
k=0
k(k 1)bk xk
bk x k 0
Simplificando, tenemos:
2
C(3x 5x ) +
k=0
[k(k 1) 2k]bk x
k1
k=0
[6 k(k 1)]bk xk 0
k=0
k(k 3)bk x
k1
k=0
(k 3)(k + 2)bk xk C(3x2 5x3 )
Realizando los cambios adecuados, se tiene:
n=1
(n + 1)(n 2)bn+1 x
n=0
(n 3)(n + 2)bn xn C(3x2 5x3 )
Expandiendo el primer trminos de la primera sumatoria, obtenemos:

0 (3)b0 x0 +
n=0
[(n + 1)(n 2)bn+1 (n 3)(n + 2)bn ]xn C(3x2 5x3 )
De la identidad anterior se sigue que b0 = 0. Por otro lado, si se hace C = 1, resulta:
n=0
[(n + 1)(n 2)bn+1 (n 3)(n + 2)bn ]xn 3x2 + 5x3
Por lo tanto, la ecuacin de recurrencia es:

bn+1 =
(n 3)(n + 2)
bn
(n + 1)(n 2)
para n = 2, 3

n = 0 b1 = 3b0
n = 1 b2 = 3b1
n = 2 (3 0)b3 (4)b2 3 b2 =
n = 3 4b4 0 b3 5 b4 =
6
b4
52
27
n = 5 b6 =
b5
63
38
n = 6 b7 =
b6
74
49
n = 7 b8 =
b7
85
..
.
n = 4 b5 =
Se puede observar que b3 = 0 y que b1 =

Por tanto, la solucin es:
3
4
7
=
12
1
=
2
9
=
20
5
4
341
3
4
b2
1
1
= , b0 = .
3
4
12
y2 =x3 ln(x) + b0 + b1 x + b2 x2 + b3 x3 + b4 x4 + b5 x5 +
1
x 3x2
5x4 3x5 7x6 x7 9x8
3
3
y2 =x ln(x) +
+
+ b3 x +
+
+
+
+
+
12 4
4
4
4
12
2
20
Como puede verse la solucin obtenida es la solucin general y = c1 y1 + c2 y2 que incluye
la primera solucin y1 = x3 . Los trminos restantes corresponden a la segunda solucin
que es equivalente a la obtenida con el primer procedimiento (dividida por 4).
EJERCICIOS 5.4.
Encuentre un conjunto fundamental de soluciones para cada una de las siguientes ecuaciones
diferenciales, indicando el intervalo de validez.
1. xy (x) 2y (x) + xy(x) = 0
7. x(1 x)y (x) + 2y (x) + xy(x) = 0
2. 2xy (x) + y (x) xy(x) = 0
8. 4x2 y (x) + 4xy (x) + (4x2 1)y(x) = 0
3. xy (x) (x 1)y (x) + y(x) = 0
9. x2 y (x) + (x2 + x)y (x) y(x) = 0
4. xy (x) y (x) + 4x2 y(x) = 0
10. 2xy (x) + (1 2x)y (x) y(x) = 0
5. x2 y (x) + xy (x) + (x2 + 4)y(x) = 0
11. x(1 x)y (x) 2y (x) + 2y(x) = 0
6. x(x2 + 2)y (x) y (x) 6xy(x) = 0
12. xy (x) + (2 x)y (x) + y(x) = 0

13. xy (x) y (x) + 4x3 y(x) = 0
14. 2x2 y (x) + (x2 x)y (x) + y(x) = 0
15. 2x2 y (x)+(2x2 3)y (x)+(x+2)y(x) =

0
1
Mediante el cambio de variable z = , encuentre la solucin general para las siguientes
x
ecuaciones diferenciales:
16. xy (x) y (x) + 4x3 y(x) = 0
17. 4x3 y (x) + 10x2 y (x) + (2x + 1)y(x) = 0
18. x4 y (x) + 2x3 y (x) + y(x) = 0
19. x4 y (x) + 2x2 (x + 1)y (x) + y(x) = 0
Suponga solucin de la forma: y =
cn xn+ para resolver la ecuacin diferencial:
n=0
20. x y (x) y (x) 2y(x) = 0

2
5.6.
ECUACIONES DIFERENCIALES NOTABLES
En diversas aplicaciones de ingeniera y ciencias resultan ecuaciones diferenciales de coeficientes variables que merecen un tratamiento especial. Esta ecuaciones aparecen en problemas
de la fsca mecnica como en las vibraciones de membranas en un tambor, en la mecnica
cuntica en la determinacin de los momentos angulares y funciones de energa de la funcin
de onda de los osciladores armnicos, entre otras.
Las soluciones de estas ecuaciones dan origen a funciones especiales como los polinomios
de Legendre, Chebyshev, Hermite, Laguerre y Bessel, que constituyen conjuntos ortogonales
en el plano de los reales, mediante los cuales se pueden interpolar funciones en un intervalo
de convergencia.
A continuacin presentaremos algunas de las ecuaciones diferenciales notables con el procedimiento para su solucin mediante series de potencias.
5.6.1.
Ecuacin diferencial de Legendre
La ecuacin diferencial de Legendre5 presenta la forma general:
(1 x2 )y (x) 2xy (x) + p(p + 1)y(x) = 0 p

/ R
Adrien-Marie Legendre(1752-1833): matemtico francs reconocido por sus aportes a la estadstica y
teora de nmeros. Investig sobre las funciones elpticas. Sus trabajos sobre races de los polinomios
inspir la teora de Galois y demostr el ltimo teorema de Fermat.
5.6. ECUACIONES DIFERENCIALES NOTABLES
343
Puede verse que la ecuacin diferencial admite soluciones de la forma de Maclaurin en el

intervalo:
I = {x R/ 1 < x < 1}
En efecto, si se suponen soluciones de la forma: y =

ck xk , resulta:
k=0
k=0
k(k 1)ck x
k2
k=0
k(k 1)ck x 2
Agrupando trminos semejantes, se tiene:
k=0
k=0
k(k 1)ck x
k2
k=0
k(k 1)ck xk2 +
k=0
kck x + p(p + 1)
k=0
k=0
ck xk 0
[k 2 + k p(p + 1)]ck xk 0
(k + p + 1)(k p)ck xk 0
Realizando el cambio de variable m = k 2 en la primera sumatoria y m = k en la segunda,

resulta:
m
(m + 2)(m + 1)cm+2 x +
(m + p + 1)(m p)cn xm 0
m=2
m=0
Sacando los dos primeros trminos de la primera sumatoria, nos queda:

0 (1)c0 x
+ 0 c1 x
(m + 2)(m + 1)cm+2 x +
m=0
m=0
De la identidad anterior se sigue que:

c0 = 0 c1 = 0 cm+2 =
(m + p + 1)(m p)
cm
(m + 1)(m + 2)
(m + p + 1)(m p)cm xm 0
con m = 0, 1, 2, . . .
Asignando algunos valores a m se tiene:

m=0
c2 =
m=1
c3 =
m=2
c4 =
m=3
c5 =
m=4
c6 =
m=5
c7 =
(0 p)(1 + p)
c0
12
(1 p)(2 + p)
c1
23
(2 p)(3 + p)
c2
34
(3 p)(4 + p)
c3
45
(4 p)(5 + p)
c4
56
(5 p)(6 + p)
c5
67
(0 p)(1 + p)
c0
2!
(1 p)(2 + p)
=
c1
3!
(0 p)(2 p)(1 + p)(3 + p)
=
c0
4!
(1 p)(3 p)(2 + p)(4 + p)
=
c1
5!
(0 p)(2 p)(4 p)(1 + p)(3 + p)(5 + p)
=
c0
6!
(1 p)(3 p)(5 p)(2 + p)(4 + p)(6 + p)
=
c1
7!
=

La solucin de la ecuacin diferencial es:
(0 p)(1 + p) 2 (0 p)(2 p)(1 + p)(3 + p) 4

y(x) =c0 1 +
x +
x +
2!
4!
(1 p)(2 + p) 3 (1 p)(3 p)(2 + p)(4 + p) 5

c1 x +
x +
x +
3!
5!
Como era de esperarse, aparecen dos soluciones linealmente independientes.

Un caso de particular de inters es aquel en el que el parmetro p es un entero no negativo, es
decir p = n con n = 0, 1, 2, 3, . . ., en el cual una de las soluciones es un polinomio de grado n,
conocido como polinomio de Legendre de primera especie y grado n, denotada como Ln (x),
mientras que la otra solucin es una serie infinita llamada funcin de Legendre de segunda
especie y grado n, denotada como Qn (x). De esta forma, la solucin general de la ecuacin de
Legendre es:
y = c1 Ln (x) + c2 Qn (x)
A continuacin se ilustran algunos casos particulares:
n = 0 y1 =1 y2 = x + 13 x3 + 15 x5 + 17 x7 + = 12 ln
1x
1+x
ln
1
2
1x
3x
2
2 3
1 5
4 7
y2 = x 3 x 5 x 35 x = 2 3x 41 ln 1+x
2
1x
1+x 5x2 2
2
4
4 6
3 8
3 5x3 3x
y2 = 1 6x + 3x + 5 x + 7 x = 2
ln 1x 2 + 3
4
2
n = 1 y1 =x y2 = 1 x
n = 2 y1 =1 3x2
1+x
1 4
x
3
1 6
x
5
1 8
x
7
5x3
3
Los polinomios normalizados de Legendre corresponden a normalizaciones de los obtenidos
previamente de tal manera que pasen por el punto (1, 1). La tabla 5.1 muestra algunos polinomios normalizados de Legendre. Las figuras 5.3(a) y 5.3(b) ilustran las grficas de los
polinomios de Legendre de grados n = 1, 2, 3, 4 de primera y segunda especie.
Los polinomios de Legendre se pueden obtener a partir de la siguiente frmula, conocida como
frmula de Rodrigue.
1 dn 2
Pn (x) = n
(x 1)n
2 n! dxn
La siguiente frmula de recurrencia6 se puede usar para determinar los polinomios de Legendre
a partir de P (x) = 1 y P (x) = x:
n = 3 y1 =x
Pn+1 (x) =
2n + 1
n
xPn (x)
Pn1 (x) n = 1, 2, 3, . . .
n+1
n+1
Puede demostrarse que:
Pn+1 (x) Pn1 (x)

2n + 1
Los polinomios de Legendre presentan ciertas propiedades, entre las que son dignas de destacar, las siguientes:
6
Tambin es vlida para Qn (x)
Pn (x)dx =

n
Pn (x)
1
(3x2
2
1
(5x3
2
3
4
5
6
7
1
(35x4
8
1
(63x5
8
1
(231x6
16
1
(429x7
16
345
1)
3x)
30x2 + 3)
70x3 + 15x)
315x4 + 105x2 5)
693x5 + 315x3 35x)
Tabla 5.1: Polinomios normalizados de Legendre
Un polinomio de Legendre es estrictamente par o impar, esto es: Pn (x) = (1)n Pn (x).
Los polinomios pares pasan por los puntos: (1, 1) y (1, 1).
Los polinomios impares pasan por los puntos: (1, 1) y (1, 1).
Todas las races de los polinomios de grado mayor o igual que uno son reales y estn en
el intervalo: 1 < x < 1.
Los polinomios son ortogonales en el intervalo: 1 < x < 1. Esto implica que:
1
0
, si m = n
Pn (x)Pm (x)dx =
2
, si m = n
1
2n + 1
La funcin generadora de los polinomios de Legendre es:
=
tn Pn (x)
1 2xt + t2
n=0
Los polinomios de Legendre se usan para interpolar funciones seccionalmente continuas en un
intervalo, es decir, funciones que no necesariamente se pueden representar en series de Taylor.
Desarrollo de una funcin mediante polinomios de Legendre
Sabemos que para desarrollar una funcin mediante una serie de potencias se requiere que
dicha funcin sea continua y tenga todas sus derivadas continuas en un entorno de cualquier

P0(x)
Q2(x)
Q0(x)
1
P1(x)
P3(x)
Q3(x)
P4(x)
-1
-1
-1
P2(x)
Q1(x)
Q4(x)
(a) Polinomios normalizados de Legendre.
(b) Polinomios de Legendre de segunda especie.
Figura 5.3: Grficas de polinomios de Legendre de primera y segunda especie
punto de su dominio.
Lo anterior significa que una funcin seccionalmente continua no se puede expresar en trminos
de series de potencias de Taylor. Veremos a continuacin que una funcin seccionalmente
continua en el intervalo 1 < x < 1 se puede expresar en trminos de los polinomios de
Legendre.
f (x) = c0 P0 (x) + c1 P1 (x) + c2 P2 (x) + + cn Pn (x) =
cn Pn (x)
n=0
Este desarrollo es conocido como desarrollo Fourier-Legendre. Los coeficientes se determinan

con base en la propiedad de ortogonalidad, as: si se multiplica la funcin por Pm (x) tenemos:
f (x)Pm (x) = c0 P0 (x)Pm (x) + c1 P1 (x)Pm (x) + c2 P2 (x)Pm (x) + + cn Pn (x)Pm (x)
Integrando en el intervalo y aplicando la propiedad de ortogonalidad, resulta:
1
1
f (x)Pm (x)dx =
cn Pn (x)Pm (x)dx para n = m
1
Despejando, tenemos:
2n + 1
cn =
2
f (x)Pn (x)dx
1
Cuando la funcin no est definida en el intervalo 1 < x < 1 sino en un intervalo cualquiera,
se puede hacer la siguiente conversin: Si f (x) est definida en el intervalo (a, b), tenemos
ba
b+a
a < x < b. Si hacemos el cambio de variable x =
t+
t, la nueva variable t estar
2
2
en el intervalo (1, 1).

Ejemplo: 5.19.
347
Considere la funcin:
0
f (x) = |x|
, si x < 1
, si 1 < x < 1
, si x > 1
Exprese la funcin mediante un desarrollo de Legendre de orden cuatro.
Solucin: Puesto que la funcin es par, su desarrollo de Legendre de orden cuatro es:
P (x) = c0 + c2 P2 (x) + c4 P4 (x)
Los coeficientes se calculan, como:
1 1
1
c0 =
|x|dx =
2 1
2

1
5
1
5 2
5
2
c2 =
|x| (3x 1)dx =
=
2 1 2
2 8
8

1
9
1
9 2
3
4
2
c4 =
|x| (35x 30x + 3)dx =
=
2 1 8
2 48
16
La interpolacin de la funcin f (x) es:
1 5 1
3 1
2
4
2
P (x) = +
(3x 1) +
(35x 30x + 3)
2 8 2
16 8
15
105 2 105 4
=
+
x
x
128
64
128
Solucin de ejemplo 5.19 con Mxima: Mxima contiene el paquete orthopoly7 que
incluye los polinomios Chebyshev, Laguerre, Hermite, Legendre, entre otros.
A continuacin se muestra la secuencia de comandos que calcula la interpolacin de una funcin f (x) en polinomios de Legendere de orden 16, usando integracin numrica de Romberg.
(%i1) f(x):=abs(x); M:16;P:0;
for n:0 thru M step 1 do
(
c[n]:((2*n+1)/2)*romberg(f(x)*legendre_p(n,x),x,-1,1),
P:P+c[n]*legendre_p(n,x)
);
7
Para cargar el paquete es necesario ejecutar el comando load(orthopoly)

Para visualizar el polinomio resultante:
(%i5) expand(P);
( %o5) 220.1447292686608 x16 + 923.6828712923015 x14 1602.221581272252 x12
+1485.582153939406 x10 795.846016388275 x8 + 249.576757650896 x6 45.21306748726688 x4
+5.536278278436516 x2 + .03642276678281531
La figura 5.4 muestra las grficas de P (x) de orden 4 y orden 16 comparadas con la funcin original f (x) = |x|.
f(x) =|x|
P(x) de orden 4
P(x) de orden 16
-1
1
0
Figura 5.4: Interpolacin de |x| en polinomios de Legendre
Como ejemplo adicional se interpola la funcin f (x) = sin(x) en polinomio de orden 7:

429 x7
x5
x3
x
( %o10) 2226799
+ 7529558253
2276213711509795
+ 14672563068765029853
903982414844
13657366323463152
14672563886840579632
5.6.2.
349
Ecuacin diferencial de Hermite
La ecuacin diferencial de Hermite8 presenta la forma general:

y (x) 2xy (x) + 2py(x) = 0 p
/ R
Por simple inspeccin se deduce que x0 = 0 es un punto ordinario de la ecuacin diferencial
y, en consecuencia, admite dos soluciones de la forma de Maclaurin, as:
y=
ck xk
k=0
Derivando dos veces y sustituyendo en la ecuacin, resulta:
k=0
k(k 1)ck x
k2
kck x + 2p
k=0
k=0
ck xk 0
La identidad anterior se puede escribir en la forma:
k=0
k(k 1)ck x
k2
k=0
(k p)ck xk 0
Expandiendo los dos primeros trminos en la primera sumatoria, nos queda:

0 (1)c0 x2 + 0 c1 x1 +
k=2
k(k 1)ck xk2 2
k=0
(k p)ck xk 0
Cambiando los ndices de la primera y segunda serie por m = k 2 y m = k respectivamente,

se sigue que:
c0 = 0 c1 = 0 cm+2 =
2(m p)
cm
(m + 2)(m + 1)
para m = 0, 1, 2, 3, . . .
Al evaluar algunos de los trminos de la serie, resultan dos soluciones que forman un conjunto
fundamental, as:
2(0 p) 2 22 (0 p)(2 p) 4 23 (0 p)(2 p)(4 p) 6
x +
x +
x +
2!
4!
6!
2(1 p) 3 22 (1 p)(3 p) 5 23 (1 p)(3 p)(5 p) 7
y2 = x +
x +
x +
x +
3!
5!
7!
y1 = 1 +
Charles Hermite(1822-1901): matemtico francs reconocido por sus aportes a la teora de nmeros.
Investig sobre interpolacin polinmica, formas cuadrticas, funciones elpticas y fue el primero
en demostrar que e es un nmero transcendente, es decir, que no es raz de ningn polinomio de
coeficientes racionales.

n
Hn (x)
2x
4x2 2
8x3 12x
16x4 48x2 + 12
32x5 160x3 + 120x
64x6 480x4 + 720x2 120
128x7 1344x5 + 3360x3 1680x
Tabla 5.2: Polinomios normalizados de Hermite
Cuando p = n, con n = 0, 1, 2, 3, . . ., una de las soluciones es un polinomio de grado: n conocido como polinomio de Hermite, mientras que la otra es una serie infinita.
Asignando algunos valores a n, se obtienen las soluciones:
x3 x5 x7
+
+
+
3
10 42
x4 x6
n = 1 y1 = x y2 = 1 x2

6
30
x3 x5
x7
n = 2 y1 = 1 2x2 y2 = x

3
30 210
2x3
x4 x6
n = 3 y1 = x
y2 = 1 3x2 +
+
+
3
2
30
La tabla 5.2 muestra algunos polinomios de Hermite. La figura 5.5 ilustra las grficas de los
polinomios de Hermite de grados n = 1, 2, 3 y 4. Los polinomios de Hermite se pueden obtener
directamente de la siguiente frmula, conocida como frmula de Rodrigue:
n
2 d
x2
Hn (x) = (1)n ex
e
dxn
A partir de los polinomios de Hermite H0 (x) = 1 y H1 (x) = 2x, se pueden determinar los
otros polinomios de Hermite, mediante la siguiente frmula de recurrencia:
n = 0 y1 = 1 y2 = x +
Hn+1 (x) = 2xHn (x) 2nHn1 (x)
Los polinomios de Hermite son ortogonales con respecto a la funcin de peso ex , as:
+
0
, si n = m
2
ex Hn (x)Hm (x)dx =
n
2 n!
, si n = m
351
H4(x)
10
H3(x)
H0(x)
-1
H1(x)
H2(x)
-10
-20
Figura 5.5: Polinomios de Hermite
Ya que los polinomios de Hermite forman un conjunto ortogonal en R2 , una funcin f (x) se
puede desarrollar, en el dominio < x < +, como una superposicin de stos, de la
siguiente manera:
f (x) = c0 H0 (x) + c1 H1 (x) + c2 H2 (x) + . . . + cn Hn (x) =
cn Hn (x)
n=0
Este desarrollo se conoce como desarrollo Fourier-Hermite. Usando la propiedad de ortogonalidad se encuentra que:
+
1
2
cn = n
ex f (x)Hn (x)dx
2 n!
La funcin generadora de los polinomios de Hermite es:
e
2txt2
Hn (x)tk
k=0
Ejemplo: 5.20.
primer orden.
k!
Encuentre la solucin general de la ecuacin diferencial de Hermite de

y (x) 2xy (x) + 2y(x) = 0
Solucin: Tal como se acaba de ver, una solucin es y1 = H1 (x) = 2x. La segunda solucin
se puede determinar de dos maneras:
Haciendo uso de los resultados previos:

y2 = 1 x2
x4 x6

6
30

Por el mtodo de reduccin de orden:
p(x)dx
2xdx
x2
e
e
x
e
x
1 x2k
y2 =H1 (x)
dx = 2x
dx =
dx =
dx
H12 (x)
(2x)2
2
x2
2
x2 k=0 k!

x
1
x2 x4 x6
=
+1+
+
+
+ dx
2
x2
2!
3!
4!
x
1
x3
x5
x7
=
+x+
+
+
+
2
x
2! 3 3! 5 4! 7
1
x4
x6
x8
2
=
1x

2
2! 3 3! 5 4! 7
Como puede verse, la solucin es la misma solucin y2 hallada previamente multiplicada

por 21 .
Solucin de ejemplo 5.20 con Mxima: Para calcular la segunda solucin mediante Mxima, con 16 trminos de la serie, digitamos los comandos:
(%i1) y2=expand(hermite(1,x)*integrate(taylor(exp(x^2)/hermite(1,x)^2,x,0,15),x)
Cuyo resultado es:
x16
( %o1) y2 = 1209600
+
x14
131040
x12
15840
x10
2160
x8
336
x6
60
x4
12
x2
2
1
2
Ejemplo: 5.21.
Con ayuda de Mxima, interpole la funcin f (x) = |x| en el rango
< x < + mediante polinomios de Hermite de orden 14.
Solucin:
Ejecutamos en siguiente cdigo:
(%i1) f(x):=abs(x); M:15;H:0;

(
c[n]:(1/(2^n*n!*sqrt(%pi)))*integrate(exp(-x^2)*f(x)*hermite(n,x),x,-inf,inf),
H:H+c[n]*hermite(n,x)
);
(%i6) expand(H);
Resultando:
x14
( %o6) 65520
13 x12
15840
143 x10
8640
143
x8
896
1001
x6
1280
1001x4
512
3003
x2
1024
429
2048
La figura 5.6 muestra la funcin f (x) y su interpolacin mediante el polinomio de hermite.
353
H(x)
2
f(x)=|x|
-2
-1
Figura 5.6: Interpolacin de f (x) = |x| mediante polinomios de Hermite de orden 14.
5.6.3.
Ecuacin diferencial de Chebyshev
La forma general de la ecuacin diferencial de Chebyshev9 es la siguiente:

(1 x2 )y (x) xy (x) + p2 y(x) = 0 p
/ R
Puesto que x0 = 0 es un punto ordinario de la ecuacin diferencial y dado que las singularidades ms cercanas son x = 1, se garantizan dos soluciones linealmente independientes en el
intervalo I = {x R/x < 1}. Tal como se estudi previamente, la ecuacin diferencial admite
soluciones de la forma: y =
ck xk .
k=0
Sustituyendo idnticamente en la ecuacin diferencial se tiene:
k=0
k(k 1)ck x
k2
k=0
k(k 1)ck x
kck x + p
k=0
k=0
ck xk 0
Agrupando las tres ltimas sumatorias se tiene:
k=0
k(k 1)ck x
k2
k=0
(k 2 p2 )ck xk 0
Pafnuti Lvvich Chebyshev(1821-1894): matemtico ruso reconocido por sus aportes en la probabilidad y estadstica. Su trabajo sobre el clculo de las races de ecuaciones le vali la medalla de
plata de la Univesidad de Mosc. Entre sus aportes importantes est el teorema de la desigualdad
de Chebyshev, usado para demostrar la cantidad de nmeros primos.

Efectuando los cambios de variable adecuados resulta:
m=2
(m + 2)(m + 1)cm+2 xm
m=0
(m2 p2 )cm xm 0
Sacando los dos primeros de la primera sumatoria, nos queda:

0 (1)c0 x2 + 0 c1 x1 +
m=0
(m + 2)(m + 1)cm+2 xm
m=0
(m2 p2 )cm xm 0
De la expresin anterior se sigue que:

c0 = 0 c1 = 0 cm+2 =
m2 p2
cm
(m + 2)(m + 1)
para m = 0, 1, 2, 3, . . .
As las cosas, la solucin de la ecuacin diferencial es:

y(x) = c0 + c1 x +
p2
1 2 p2
p2 (22 p2 ) 4 (12 p2 )(32 p2 ) 5
c0 x2 +
c1 x3 +
c0 x +
c1 x +
2!
3!
4!
5!
En consecuencia, las soluciones de la ecuacin diferencial son:

p2 2 p2 (2 p2 ) 4 p2 (2 p2 )(42 p2 ) 6
x +
x +
x +
2!
4!
6!
12 p2 3 (12 p2 )(32 p2 ) 5 (12 p2 )(32 p2 )(52 p2 ) 7
y2 =x +
x +
x +
x +
3!
5!
7!
y1 =1 +
Particularmente, cuando p = n = 0, 1, 2, . . ., una de las soluciones es un polinomio Tn (x) de

grado n conocido como polinomio de Chebyshev de primera especie y la otra es una serie infinita que se escribe en trminos de unos polinomios conocidos como polinomios de Chebyshev
de segunda especie.
Asignando algunos valores a n se obtiene:
x3 3x5 5x7
+
+
+ = sin1 (x)
6
40
112
x2 x4 x6 5x8
= x y2 = 1
= 1 x2
2
8
16 128
3
x
x5 x7 5x9
= 1 2x2 y2 = x
= x 1 x2
2
8
16 128
2
4
3
9x
15x
7x6 27x8
= x x y2 = 1
+
+
+
+ = (4x2 1) 1 x2
2
2
8
16
128
3
5
7
5x
9x
33x
= 1 8x2 + 8x4 y2 = x
+
+
+ = 4(8x3 4x) 1 x2
2
8
64
n = 0 y1 = 1 y2 = x +
n = 1 y1
n = 2 y1
n = 3 y1
n = 4 y1
355
Tn (x)
Un (x)
2x
1 2x2
4x2 1
4x3 3x
8x3 4x
8x4 8x2 + 1
16x4 12x2 + 1
16x5 20x3 + 5x
32x5 32x3 + 6x
32x6 48x4 + 18x2 1
64x6 80x4 + 24x2 1
64x7 112x5 + 56x3 7x
128x7 192x5 + 80x3 8x
Tabla 5.3: Polinomios normalizados de Chebyshev de primera y de segunda especie.
La solucin general de la ecuacin diferencial de Chebyshev se escribe como:
c1 Tn (x) + c2 1 x2 Un1 (x) , para n = 1, 2, 3, . . .

y=
c1 Tn (x) + c2 sin1 (x)
, para n = 0
Los polinomios de Chebyshev se pueden determinar a partir de la frmula:
Tn (x) = cos n cos1 (x)

, si |x| 1
1 x2 Un (x) = sin (n + 1) cos1 (x)

, si |x| 1
Tambin se pueden expresar en la forma:

n n2
n n4
n
2
Tn (x) =x
x (1 x ) +
x (1 x2 )2
2
4
n+1 n
n + 1 n2
n + 1 n4
2
Un (x) =
x
x (1 x ) +
x (1 x2 )2
1
3
5
Los polinomios normalizados de Chebyshev Tn (x) corresponden a normalizaciones de los obtenidos previamente de tal manera que pasen por el punto (1, 1).
La tabla 5.3 muestra algunos polinomios normalizados de Chebyshev y las figuras 5.7(a) y
5.7(b) ilustran las grficas de los polinomios de grados n = 1, 2, 3 y 4 de primera y segunda especie. La siguiente frmula de recurrencia10 permite hallar cualquier polinomio de Chebyshev
a partir de T0 (x) = 1 y T1 (x) = x.
Tn+1 (x) = 2xTn (x) + Tn1 (x) n = 1, 2, 3, . . .
10
Tambin se cumple para Un (x)
T3(x)
T0(x)
T4(x)
!(1-x2)U2(x)
!(1-x2)U0(x)
T1(x)
sin-1(x)
0
T2(x)
!(1-x2)U1(x)
-1
(a) Polinomios normalizados de Chebyshev de primera

especie Tn (x).
!(1-x2)U3(x)
-1
(b) Soluciones sin1 (x) y
1 x2 Un (x).
Figura 5.7: Soluciones de la ecuacin de Chebyshev
Las siguientes ecuaciones de recurrencia relacionan los polinomios de primera y segunda especie:
Tn (x) = Un (x) xUn1 (x)
(1 x )Un (x) = xTn (x) Tn+1 (x)
2
Los polinomios de Chebyshev son ortogonales11 en el intervalo: 1 < x < 1 con respecto a la
1
funcin de peso (1 x2 ) 2 , as:
1
0 , si n = m
Tn (x)Tm (x)
dx = , si n = m = 0
1 x2
1
, si n = m
2
Al igual que los polinomios de Legendre, los polinomios de Chebyshev se pueden usar para
desarrollar funciones seccionalmente continuas en el intervalo 1 < x < 1, en la forma:
c0
C0
f (x) = T0 (x) + c1 T1 (x) + c2 T2 (x) + + cn Tn (x) =
+
cn Tn (x)
2
2
n=1
Este desarrollo se conoce como desarrollo Fourier-Chebyshev. Usando la propiedad de ortogonalidad, se determinan los coeficientes de la serie, resultando:
2 1 f (x)Tn (x)
cn =
dx para n=0,1,2,3,. . .
1 1 x2
11
Los Un (x) tambin son ortogonales pero con respecto a la funcin de peso
1 x2
357
Precisamente, se usan a menudo en el diseo de filtros pasivos.

La funcin generadora de los polinomios de Chebyshev es:
1 tx
=
Tn (x)tk
1 2tx + t2
k=0
Los polinomios de Chebyshev presentan ciertas propiedades, entre las que son dignas de
destacar, las siguientes:
Un polinomio de Chebyshev es estrictamente par o impar, esto es: Tn (x) = (1)n Tn (x).
Los polinomios pares pasan por los puntos: (1, 1) y (1, 1).
Los polinomios impares pasan por los puntos: (1, 1) y (1, 1).
Todas las races de los polinomios de grado mayor o igual que uno son reales y estn en
el intervalo 1 < x < 1.
Ejemplo: 5.22.
Con ayuda de Mxima, interpole la funcin f (x) = |x| en el rango
1 < x < 1 mediante polinomios de Chebyshev de orden 15.
Solucin:
Ejecutamos en siguiente cdigo:
(%i1) f(x):=abs(x); M:15;

I:(2/%pi)*quad_qags(f(x)*chebyshev_t(0,x)/sqrt(1-x^2),x,-1,1);
c[0]:I[1];T:c[0]/2;
(
I:(2/%pi)*quad_qags(f(x)*chebyshev_t(n,x)/sqrt(1-x^2),x,-1,1),
c[n]:I[1],
T:T+c[n]*chebyshev_t(n,x)
);
(%i6) expand(T);
Resultando:
x15
x14
x13
x12
x11
( %o6) .006893693852583105
+ 168.0232459311857
0.025853012321044
645.3680780706402
+ 0.0387824385700343
x10
x9
x8
x7
x6
+ 1001.158891636406
.02962812580925847
804.5131024112843
+ .01212190830198423
+ 358.3795880970659
x5
x4
104 x3
x2
106 x
.002545940467880352
89.59659848209887
+ 2.3577503940887526
+ 14.93312077557788
6.316798858618144
+ 0.133335501789843
T(x)
1
f(x)=|x|
-1
1
0
Figura 5.8: Interpolacin de f (x) = |x| mediante polinomios de Chebyshev de orden 15.
La figura 5.8 muestra la funcin f (x) y su interpolacin mediante el polinomio de Chebyshev.

Ejemplo: 5.23.
primer orden.
Encuentre la solucin general de la ecuacin diferencial de Chebyshev de

(1 x2 )y (x) xy (x) + y(x) = 0
Solucin: Con base en lo estudiado previamente, las dos soluciones de la ecuacin diferencial
son:
x2 x4 x6 5x8

2
8
16 128
La segunda solucin tambin se puede determinar mediante el mtodo de reduccin de orden
as:
x
1x
1 ln(1x2 )
dx
2
e
e 2
1
y2 =C1 (x)
dx = x
dx
=
x
dx
2
C1 (x)
x2
x2 1 x2
= 1 x2
y1 = T1 (x) = x y2 = 1
La solucin se puede expresar en series de potencias como:
x2 x4 x6 5x8
2
1x = 1

2
8
16 128
La cual es la misma solucin hallada previamente pero con signo negativo.

Finalmente la solucin general de la ecuacin de Chebyshev de primer orden es:
y = c1 x + c2 1 x2 = c1 T1 (x) + c2 1 x2 U0 (x)
5.6.4.
359
Ecuacin diferencial de Laguerre
La ecuacin diferencial de Laguerre12 presenta la forma general:

xy (x) + (1 x)y (x) + py = 0 p
/ R
Como puede verse, el punto: x0 = 0 es un punto singular regular de la ecuacin diferencial y,
en consecuencia, admite al menos una solucin de la forma de Frobenius, as:
y=
ck xk+
k=0
Derivando dos veces y sustituyendo en la ecuacin diferencial se tiene:
k=0
(k + 1)(k + )ck xk+1 +
k=0
(k + )ck xk+1
(k + )ck xk+ +
k=0
k=0
pck xk+ 0
Agrupando sumatorias y sacando como factor comn x , resulta:
(k + ) ck x
k=0
k1
k=0
(k p)ck xk 0
Realizando los cambios de variables adecuados, obtenemos:
m=1
(m + + 1)2 cm+1 xm
m=0
(m p)cm xm 0
Expandiendo el primer trmino de la primera sumatoria y agrupando sumatorias, resulta:

2 c0 x1 +
m=0
[(m + + 1)2 cm+1 (m + p)cm ]xm 0
Para soluciones diferentes de la trivial, se toma c0 = 0, con lo que resulta: 1 = 2 = 0 y, por
tanto se tiene una solucin de la forma: y1 =

cm xm .
m=0
Para el valor dado de la ecuacin de recurrencia es:

cm+1 =
mp
cm
(m + 1)2
m = 0, 1, 2, 3, . . .
12
Edmond Nicolas Laguerre(1834-1886):matemtico francs reconocido por sus aportes en la geometra

y el anlisis matemtico. Hizo carrera militar y fue catedrtico de fsica matemtica en el Colegio de
Francia.

Evaluando algunos trminos, resulta:
p
p(1 p) 2 p(1 p)(2 p) 3 p(1 p)(2 p)(3 p) 4
y1 = c0 1
x
x
x
x
(1!)2
(2!)2
(3!)2
(4!)2
La segunda solucin se puede determinar mediante mtodo propuesto en 5.5.4 o por reduccin
de orden.
Particularmente, cuando p = n = 0, 1, 2, 3, . . . la solucin hallada es un polimonio de grado n,
as:
n = 0 y1 = 1
n = 1 y1 = 1 x
1
n = 2 y1 = 1 2x + x2
2
3
1
n = 3 y1 = 1 3x + x2 x3
2
6
2
1
n = 4 y1 = 1 4x + 3x2 x3 + x4
3
24
5
4
3
x
5x
5x
n = 5 y1 =
+
+ 5x2 5x + 1
120
24
3
x6
x5 5x4 10x3 15x2
n = 6 y1 =
+
6x + 1
720 20
8
3
2
x7
7x6 7x5 35x4 35x3 21x2
n = 7 y1 =
+
+
7x + 1
5040 720
40
24
6
2
La solucin polinmica recibe el nombre de polinomio de Laguerre de grado n. La tabla 5.4
muestra algunos polinomios de Laguerre y la figura 5.9 ilustra las grficas de los polinomios
de grados n = 1, 2, 3 y 4. Puede verse que todas las races de los polinomios se ubican en
x > 0. Los polinomios de Laguerre se pueden determinar a partir de la siguiente frmula,
conocida como frmula de Rodrigue:
Ln (x) = ex
dn n x
(x e )
dxn
La siguiente frmula de recurrencia permite hallar cualquier polinomio de Laguerre a partir

de L0 (x) = 1 y L1 (x) = 1 x.
Ln+1 (x) = (2n + 1 x)Ln (x) n2 Ln1 (x) n = 1, 2, 3, . . .
Los polinomios de Laguerre son ortogonales para x > 0 con respecto a la funcin de peso ex ,
as:

0
, si n = m
ex Ln (x)Lm (x)dx =
2
(n!)
, si n = m
0

n
Ln (x)
x + 1
1
(x2
2
1
(x3
6
1
(x4
24
1
(x5
120
1
(x6
720
6
7
1
(x7
5040
361
4x + 2)
+ 9x2 18x + 6)
16x3 + 72x2 96x + 24)
+ 25x4 200x3 + 600x2 600x + 120)
36x5 + 450x4 2400x3 + 5400x2 4320x + 720)
+ 49x6 882x5 + 7350x4 29400x3 + 52920x2 35280x + 5040)

Tabla 5.4: Polinomios de Laguerre
Los polinomios de Laguerre se pueden usar para desarrollar funciones en el intervalo x > 0,
en la forma:
f (x) = c0 L0 (x) + c1 L1 (x) + c2 L2 (x) + + cn Ln (x) =

cn Ln (x)
n=0
Este desarrollo se conoce como desarrollo Fourier-Laguerre. Usando la propiedad de ortogonalidad, se determinan los coeficientes de la serie, resultando:

1
cn =
ex f (x)Ln (x)dx
(n!)2 0
Ejemplo: 5.24.
de la ecuacin:
Usando el mtodo de reduccin de orden, determine la segunda solucin
Solucin:
La primera solucin es: y1 = 1 x.
xy (x) + (1 x)y (x) + y = 0
En cuanto a la segunda solucin, tenemos:

1x dx
ln(x)+x
x
e
e
ex
y2 =(1 x)
dx
=
(1
x)
dx
=
(1
x)
dx
(1 x)2
(1 x)2
x(1 x)2

1
11x 49x2 87x3 1631x4 11743x5
=(1 x)
+3+
+
+
+
+
+ dx
x
2
6
8
120
720
11x2 49x3 87x4 1631x5

=(1 x) ln(x) + 3x +
+
+
+
+
4
18
32
600
x2 x3
x4
x5
x6
=(1 x) ln(x) + 3x

4
36 288 2400 21600
L3(x)
2
L4(x)
1
L0(x)
L1(x)
L2(x)
-1
Figura 5.9: Polinomios de Laguerre
5.6.5.
Ecuacin diferencial de Bessel
La ecuacin diferencial de Bessel13 presenta la forma general:

x2 y (x) + xy (x) + (x2 p2 )y(x) = 0
con p
/ R
Por simple inspeccin se ve que x0 = 0 es un punto singular regular de la ecuacin diferencial
y, en consecuencia, se garantiza al menos una solucin de la forma: y =

ck xk+ .
k=0
La solucin ser vlida en el intervalo: x > 0.
A sustituir idnticamente en la ecuacin diferencial resulta:
k=0
(k + 1)(k + )ck x
k+
k=0
(k + )ck x
k+
k=0
ck x
k++2
k=0
ck xk+ 0
13
Friedrich Wilhelm Bessel(1784-1846): matemtico y astrnomo alemn reconocido por sus aportes
en la medicin y catalogacin de ms de 75mil estrellas, precisiones en la rbita del cometa Halley, en
la navegacin martima y en la sistematizacin de las funciones de Bessel, que llevan su nombre pese
a ser descubiertas por Daniel Bernoulli. De origen humilde paso de ser aprendiz en una compaia
mercantl, a contador, y finalmente a director del observatorio de Kaliningrado, Rusia.
363
Agrupando sumatorias y sacando como factor comn x resulta:
ck x
k+2
k=0
k=0
[(k + )2 p2 ]ck xk 0
Realizando los cambios de variable adecuados y factorizando, se tiene:
cm2 xm +
m=0
m=0
[(m + + p)(k + p)]cm xm 0
Equivalentemente se puede escribir, como:

0
(+p)(p)c0 x +(1++p)(1+p)c1 x +
m=2
([(m + + p)(m + p)]cm + cm2 ) xm 0
Para obtener soluciones no triviales se impone la condicin c0 = 0, con lo que resulta la

ecuacin indicial:
( + p)( p) = 0
De donde las soluciones son 1 = p y 2 = p. De acuerdo a lo estudiado en la seccin 5.5.2,

tomando la mayor raz obtenemos una solucin.
Para 1 = p la ecuacin de recurrencia nos queda:
(1 + 2p)c1 = 0 cm =
cm2
m(m + 2p)
para m = 2, 3, 4 . . .
De aqu se tiene que c1 = 0 si p = 12 . Evaluando algunos trminos, obtenemos:

c0
c0
= 2
2(2 + 2p)
2 (1 + p)
c1
m = 3 c3 =
= 0 y consecuentemente: c3 = c5 . . . = 0
3(3 + p)
c2
c2
c0
m = 4 c4 =
= 3
= 4
4(4 + 2p)
2 (2 + p)
2 2!(1 + p)(2 + p)
c4
c4
c0
= 6
m = 6 c6 =
= 2
6(6 + 2p)
2 3!(2 + p)
2 3!(1 + p)(2 + p)(3 + p)
..
.
m = 2 c2 =
m = 2k c2k =
(1)k
c0
22k k!(p + 1)(p + 2)(p + 3) (p + k)
Por tanto la solucin nos queda:
x2
x4
x6
p
y1 = c0 x 1 2
+
+
2 (1 + p) 24 2!(1 + p)(2 + p) 26 3!(1 + p)(2 + p)(3 + p)

La solucin se puede escribir como:
y1 = c0 x
k=0
x 2k
(1)k
k!(p + 1)(p + 2)(p + 3) (p + k) 2
El producto sucesivo (p + 1)(p + 2)(p + 3) (p + k) se puede escribir en forma general para

cualquier valor de p = 1, 2, 3, . . . en trminos de la funcin gamma14 , as:
(p + k + 1) = (p + k)(p + k 1)(p + k 2) (p + 3)(p + 2)(p + 1)(p + 1)
Con lo cual, la solucin nos queda:
x 2k+p
(p + 1)
(1)k
y1 =
c0
2p
k!(p + k + 1) 2
k=0
La serie encontrada recibe el nombre de funcin de Bessel de primera especie de orden p y se

denota como:
x 2k+p
(1)k
Jp (x) =
(5.8)
k!(p
+
k
+
1)
2
k=0
Por lo tanto, la primera solucin es: y1 = Jp (x).

Cuando p = n = 0, 1, 2, 3, . . ., la funcin gamma se convierte en factorial y la solucin puede
escribirse como:
(1)k x 2k+n
y1 = Jn (x) =
k!(n + k)! 2
k=0
En la figura 5.10 se ilustran algunos polinomios de Bessel para n = 0, 1, 2, 3, 4 y p = 14 , 13 , 12 .
Como puede verse, los polinomios de Bessel son funciones continuas oscilatorias que decrecen a
medida que x aumenta. Si p es un negativo no entero, los polinomios de Bessel son oscilatorios
pero con una discontinuidad en x = 0.
En cuanto a la segunda solucin, es decir, para 2 = p, se tiene:
cm2
(1 2p)c1 = 0 cm =
para m = 2, 3, 4 . . .
m(m 2p)
Como puede verse, si p = 12 la constante c1 es diferente de cero y en consecuencia resultan

dos soluciones linealmente independientes. Para cualquier otro valor de p se tiene que c1 = 0.
Analizando la ecuacin de recurrencia se concluye que si p = n = 0, 1, 2, 3, . . ., es imposible
hallar una segunda solucin, ya que el resultado es linealmente dependiente con la primera,
de hecho se puede demostrar que: Jn (x) = (1)n Jn (x)15 . En este caso la segunda solucin,
usando reduccin de orden, est dada por:
1
y2 = Jn (x)
dx
2
xJn (x)
14
15
Remtase al apndice A.2

Remtase al ejemplo 5.25
365
J0(x)
J1/4(x)
J1/3(x)
J1(x)
J2(x)
J3(x)
J4(x)
J1/2(x)
J-1/2(x)
0
0
J-1/3(x)
J-1/4(x)
(a) Polinomios de Bessel de orden entero
(b) Polinomios de Bessel de orden fraccionario
Figura 5.10: Polinomios de Bessel de primera especie y orden p
Esta solucin se conoce como funcin de Bessel de segunda especie y orden n, denotada como
Yn (x)16 . Como se puede ver en la figura 5.11, dichas funciones divergen en x = 0. Usando
el mtodo propuesto en la seccin 5.5.4 se puede demostrar que la solucin se puede escribir
como:
n1
2 x
1 (n k 1)! x 2kn
ln
Jn (x)
2
k=0
k!
2
x 2k+n
1 (1)k
[(k + 1) + (n + k + 1)]
k=0 k!(n + k)!
2
Yn (x) =
Con (n) =
(n)
(n)
= +
n1
k=1
1
k
conocida como la funcin Digamma.
Tambin suelen escribirse ms compactamente como:

Jp (x) cos(p) Jp (x)
pn
sin(p)
Yn (x) = lm
Con esto, la solucin general de la ecuacin diferencial est dada por: y = c1 Jn (x) + c2 Yn (x).
En otro caso, para p = 0, 1, 2, 3, . . ., puede verse que la segunda solucin es:
Jp (x) =
16
k=0
x 2kp
(1)k
k!(p + k + 1) 2
Tambin conocida como funcin de Weber o Neumman

Y0(x)
Y1(x)
Y2(x) Y (x)
Y4(x)
3
Figura 5.11: Polinomios de Bessel de segunda especie y orden n
Por lo tanto, la solucin general de la ecuacin diferencial es:

y = c1 Jp (x) + c2 Jp (x)
En conclusin, dada la ecuacin diferencial: x2 y (x) + xy (x) + (x2 p2 )y(x) = 0 .
La solucin es:
c1 Jp (x) + c2 Jp (x) para p = 0, 1, 2, 3, . . .

y=
c1 Jn (x) + c2 Yn (x)
para p = n = 0, 1, 2, 3, . . .
Los polinomios de Bessel son soluciones de diversos problemas en geometrias cilndricas. Estos
forman un conjunto ortogonal mediante el cual se puede desarrollar una funcin f (x). Existen
tres maneras de realizar el desarrollo, una de ellas es:
f (x) = a1 Jn (1 x) + a2 Jn (2 x) + a3 Jn (3 x) + + ak Jn (k x) =
ak Jn (k x)
k=1
Donde los valores 1 , 2 , . . . , k son las soluciones de la ecuacin Jn (x) = 0, es decir, los interceptos del polonimio Jn (x). En la tabla 5.5 se muestran algunos interceptos de los polinomios
de Bessel. Estos interceptos son de gran utilidad en Telecomunicaciones para el ajuste de la
desviacin mxima de frecuencia de una seal modulada en frecuencia FM.
Y los coeficientes se calculan mediante:
2
ak = 2
Jn+1 (k )
xf (x)Jn (k x)dx
0
La funcin generadora de los polinomios de Bessel es:

e
x
(t 1t )
2
k=
Jn (x)tn
367
Jn (x)
J0 (x)
2.4048
5.5201
8.6537
11.7915
14.9309
18.0711
J1 (x)
3.8317
7.0156
10.1735
13.3237
16.4706
19.6159
J2 (x)
5.1356
8.4172
11.6198
14.7960
17.9598
19.6159
J3 (x)
6.3802
9.7610
13.0152
16.2235
19.4094
22.5827
J4 (x)
7.5883
11.0647
14.3725
17.6160
20.8269
24.0190
J5 (x)
8.7715
12.3386
15.7002
18.9801
22.2178
25.4303
J6 (x)
9.9361
13.5893
17.0038
20.3208
23.5861
26.8202
Tabla 5.5: Interceptos de los polinomios de Bessel
Se puede demostrar que la transformada de Laplace de los polinomios de Bessel de primera

especie es:
n
s 2 + a2 s
L {Jn (at)} =
con n Z+
an s 2 + a2
Las funciones de Bessel poseen algunas propiedades importantes, entre las que podemos destacar las siguientes:
Relaciones integrales:
sin(p) x sinh()p
1
cos (p x sin())d
e
d
2
0
0
Jp (x) =
1 cos (n x sin())d
2
Jp (x) =
(p +
1
)
2
2p1
x
0
(x2 2 )
J (x)J (x)
2 sin 2 ( )
dx =
0
x
2 2
xJn (x)Jn (x)dx =
p 12
cos()d para p > 12
x [Jn (x)Jn (x) Jn (x)Jn (x)]

2 2
xn Jn1 (x)dx = xn Jn (x)
Ecuaciones de recurrencia:
1
2
, para p = n = 0, 1, 2, . . .
, para p >

2p
Jp (x) Jp1 (x)
x
xJp (x) = pJp (x) xJp+1 (x)
d p
[x Jp (x)] = xp Jp1 (x)
dx
2Jp (x) = Jp1 (x) Jp+1 (x)
Jp+1 (x) =
k
1
2 x
Jp (x) =
(1 )
Jp+n (x)
2
k=0 k!
p
xJp (x) = xJp1 (x) pJp (x)

Relacin con funciones trigonomtricas:
J1/2 (x) =
Jn+ 1 =
2
2
sin(x)
x
J1/2 (x) =
2
cos(x)
x

n+1
n2k
2
2
2
(n k)! 12 k
nk
(1)
sin(x)
x k=0
x
k!
n 2k
n+12k
2
(n k)!
12 k
k
cos(x)
x
k!
n + 1 2k
Ejemplo: 5.25.
Demuestre la propiedad: Jn (x) = (1)n Jn (x)
x 2kn
(1)k
Solucin: Partimos de la funcin de Bessel: Jn (x) =
k=0 k!(n + k)! 2
Realizando el cambio de variable: j = k n, nos queda:
Jn (x) =
(1)j+n x 2j+n
(j + n)!j! 2
j=n
Jn (x) =
(1)j+n x 2j+n
(1)j x 2j+n
+ (1)n
(j + n)!j! 2
(j + n)!j! 2
j=n
j=0
Teniendo en cuenta que el factorial de un nmero negativo tiende a , la primera sumatoria

tiende a cero y, en consecuencia queda demostrada la propiedad.
Ejemplo: 5.26.
Demuestre la propiedad:
d p
[x Jp (x)] = xp Jp1 (x)
dx
369
p
Solucin: Derivando la funcin x Jp (x) tenemos:
x 2k+p
k
k
d p
d
(1)
d
(1)
[x Jp (x)] =
xp
=
x2(k+p)
2k+p k!(p + k + 1)
dx
dx
k!(p
+
k
+
1)
2
dx
2
k=0
k=0
(1)k 2(k + p)
(1)k
2(k+p)1
=
x
=
x2(k+p)1
2k+p
2k+p1
2
k!(p + k)(p + k)
2
k!(p + k)
k=0
k=0
(1)k x 2k+p1
= xp
= xp Jp1 (x)
k!(p
+
k)
2
k=0
EJERCICIOS 5.5.
Encuentre la solucin general para las ecuaciones diferenciales:

1. (1 x2 )y (x) 2xy (x) + 6y(x) = 0
3
2. (1 x2 )y (x) 2xy (x) + y(x) = 0
4
1
6. (1 x2 )y (x) xy (x) + y(x) = 0
4
7. xy (x) + (1 x)y (x) + 2y(x) = 0
3. y (x) 2xy (x) + 4y(x) = 0
1
8. xy (x) + (1 x)y (x) + y(x) = 0
2
4. y (x) 2xy (x) + y(x) = 0
9. x2 y (x) + xy (x) + (x2 4)y(x) = 0
5. (1 x2 )y (x) xy (x) + 4y(x) = 0
10. x2 y (x) + xy (x) + (x2 0.25)y(x) = 0
11. Use los polinomios normalizados de Legendre para aproximar la funcin f (x) = 1 |x|
en el intervalo 1 x 1. Represente grficamente la funcin original en un mismo
grfico con la aproximacin.
12. Demuestre las siguientes propiedades:
a) xJp (x) = pJp (x) xJp+1 (x)
b) 2Jp (x) = Jp1 (x) Jp+1 (x)

2p
c) Jp+1 (x) = Jp (x) Jp1 (x)
x
13. Usando la propiedad de recurrencia, exprese J3 (x) en trminos de J0 (x) y J1 (x).

14. Evale las siguientes integrales:
a) xJ0 (x)dx
b) x2 J1 (x)dx
c)
x4 J1 (x)dx
d)
xJ02 (x)dx
15. Considere la ecuacin diferencial (1 x2 )y (x) + xy (x) + (2 x2 p2 )y(x) = 0, conocida

como ecuacin paramtrica de Bessel con parmetro . Demuestre que la funcin: Jn (x)
es una solucin de la ecuacin diferencial.

16. Usando el hecho de que (n + 12 ) =
funcin de Bessel, demuestre que:
2
a) J1/2 (x) =
sin(x)
(2n 1)!
con n = 1, 2, 3, . . . y la frmula de la
2n
b) J1/2 (x) =
2
cos(x)
17. Usando las ecuaciones de recurrencia, exprese J3/2 (x) y J5/2 (x) en trminos de J1/2 (x)
y J1/2 (x).

Ecuaciones Cap5

Hochgeladen von

Dokumentinformationen

Originaltitel

Copyright

Verfügbare Formate

Dieses Dokument teilen

Dokument teilen oder einbetten

Freigabeoptionen

Stufen Sie dieses Dokument als nützlich ein?

Sind diese Inhalte unangemessen?

Copyright:

Verfügbare Formate

Ecuaciones Cap5

Hochgeladen von

Copyright:

Verfügbare Formate

Captulo

Una ecuacin diferencial de coeficientes variables presenta la forma geneeral:

En la expresin anterior se tiene que: {y1 , y2 , . . . , yn } es un conjunto fundamental de soluciones

LA ECUACIN DIFERENCIAL DE EULER

La ecuacin diferencial de Euler1 de orden n presenta la forma general:

[an xn Dn + an1 xn1 Dn1 + an2 xn2 Dn2 + + a1 xD + a0 ]y(x) = f (x)

298 CAPTULO 5. ECUACIONES DIFERENCIALES DE COEFICIENTES VARIABLES

La ecuacin diferencial de Euler de segundo orden

La ecuacin diferencial de Euler de segundo orden presenta la forma general:

El intervalo de validez de la solucin de la homognea es I = {x R / x = 0}. Para determinar

5.2. LA ECUACIN DIFERENCIAL DE EULER

Encuentre la solucin general de la siguiente ecuacin diferencial en el

Primero que todo se escribe la ecuacin caracterstica, as:

La ecuacin se puede escribir en forma factorizada, as:

300 CAPTULO 5. ECUACIONES DIFERENCIALES DE COEFICIENTES VARIABLES

Retornando a la variable original, la solucin general nos queda:

La ecuacin diferencial de Euler de tercer orden

La ecuacin diferencial de Euler de tercer orden presenta la forma general:

La ecuacin caracterstica de la homognea asociada es:

5.2. LA ECUACIN DIFERENCIAL DE EULER

4. Dos races son complejas conjugadas y la otra es real: 1 , 2 , 3 = j

Encuentre la solucin general de la siguiente ecuacin diferencial en el

Solucin: Primero que todo se escribe la ecuacin caracterstica, as:

La ecuacin se puede escribir en forma factorizada, as:

La solucin particular es de la forma: yss = 1 y1 + 2 y2 + 3 y3 , por tanto:

302 CAPTULO 5. ECUACIONES DIFERENCIALES DE COEFICIENTES VARIABLES

Regresando a la variable original, la solucin general nos queda:

1. La ecuacin caracterstica es:

5.2. LA ECUACIN DIFERENCIAL DE EULER

3. La ecuacin caracterstica es:

Ecuaciones diferenciales reducibles a Euler

Algunas ecuaciones diferenciales se pueden reducir a ecuaciones de Euler mediante un cambio

Con base en lo estudiado previamente, el intervalo de validez de la solucin es:

304 CAPTULO 5. ECUACIONES DIFERENCIALES DE COEFICIENTES VARIABLES

a z y (z) + aczy (z) + dy(z) = f

Encuentre la solucin general de la ecuacin diferencial:

Solucin: Al efectuar el cambio de variable z = 2x + 1 resulta la ecuacin diferencial:

4z 2 y (z) + 4zy (z 4y(z) = z + 1 z 2 y (z) + zy (z) y(z) =

La ecuacin caracterstica es:

Retornando a la variable z, nos queda:

Y finalmente regresando a la variable original, la solucin general es:

5.2. LA ECUACIN DIFERENCIAL DE EULER

9. (2x 3)2 y + 8(2x 3)y + 8y = 0

10. (2x + 3)2 y + 10(2x + 3)y + 8y = 0

Resuelva cada uno de los siguientes problemas de valor inicial.

14. x3 y + 3x2 y + xy = 0 y(1) = 0 , y (1) = 1 , y (1) = 0

306 CAPTULO 5. ECUACIONES DIFERENCIALES DE COEFICIENTES VARIABLES

En su forma expandida es:

En la expresin anterior, aparece un polinomio de grado N que se utiliza para aproximar la

La convergencia implica que:

Clculo de los coeficientes de la serie

5.3. SERIES DE POTENCIA

verifican las siguientes identidades:

308 CAPTULO 5. ECUACIONES DIFERENCIALES DE COEFICIENTES VARIABLES

Es posible determinar la serie de Maclaurin de cualquier funcin mediante el clculo directo

La funcin dada se puede escribir en la forma:

Haciendo uso de la serie de la funcin ln(1 x), resulta:

El intervalo de convergencia viene dado por:

I = x R/ < 1 = x R/|x| <

5.3. SERIES DE POTENCIA

Si deseamos encontrar la expresin en series de potencias, ejecutamos el comando:

Solucin de ejemplo 5.5 con Matlab: Usando MATLAB es comando es el mismo,

Multiplicacin de series de potencias