Beruflich Dokumente
Kultur Dokumente
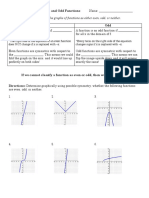
Multi Variable Calculus
Hochgeladen von
hemanthCopyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Multi Variable Calculus
Hochgeladen von
hemanthCopyright:
Verfügbare Formate
MATHEMATICS-I (MA1L001)
Calculus of Several Variables
(July-December 2015)
by
Dr. Sabyasachi P ani
(Assistant Professor in Mathematics)
School of Basic Sciences
IIT BHUBANESWAR
Autumn Semester-2015-16
Syllabus of Mathematics-1 IIT Bhubaneswar
MATHEMATICS-1(Syllabus-July-Dec 2015)
Differential Calculus of single variable: Rolles theorem, Lagranges Mean Value Theorem,
Cauchys mean value theorem (Taylors and Maclaurin theorems with remainders), Indeterminate
forms, maxima and minima of a function, Concavity and convexity of a curve, points of inflexion,
curvature, asymptotes and curve tracing (Cartesian and Polar).
Differential Calculus of Several Variables: Limit, continuity and differentiability of functions of
several variables, partial derivatives and their geometrical interpretation, differentials, derivatives of
composite and implicit functions, derivatives of higher order and their commutativity, Eulers theorem
on homogeneous functions, harmonic functions, Taylors expansion of functions of several variables,
maxima and minima of functions of several variables, Lagranges method of multipliers.
Multiple Integrals and Vector Calculus: Double and triple integrals, Scalar and vector fields,
level surfaces, directional derivative, Gradient, Curl, Divergence, line and surface integrals, theorems
of Green, Gauss and Stokes. Beta and Gamma functions.
Ordinary Differential Equations: First order differential equations, exact, reducible to exact,
homogeneous, reducible to homogeneous, linear equations, and Bernoullis form, second order
differential equations with constant coefficients, getting a LI solution if one solution is known, Eulers
equations, finding particular integrals (method of undetermined coefficients, variation of parameters,
operator methods), system of differential equations.
Information about Mathematics-1, IIT Bhubaneswar
MATHEMATICS-1
(Teaching team and Examinations and Grading)
Teaching Team: Dr. A K Ojha, Dr A D Banik and Dr. S Pani.
(Lecture Hours: 3, Tutorial Hour: 1, Practice:0, Credit :4)
Tutorials Instructors: Mr. B K Sahu, Mr. N B Barik,
Mr. Subhasih Nayak, Mr. Gopinath Sahu.
Examination Pattern:
Mid Semester Exam
30% marks
2 hours closed book
End Semester Exam
50% marks
3 hours closed book
Teachers Assessment
20%
By
tutorial
tests,
discipline,
interactions,
attendance, assignment,
etc.
AT THE END YOU WILL BE AWARDED WITH A GRADE.
(EX-10 points, A-9 points, B-8 points, C-7 points, D-6 points, P-5 points, F: 0 points (fail grade), Iincomplete, etc)
3
Information about Mathematics-1, IIT Bhubaneswar
MATHEMATICS-1
(Books and Topics to be followed from Books)
Text and Reference Books
Differential Calculus and Integral Calculus, Shanti Narayan and M ittal , S. Chand & Company Ltd,
Calculus and Analytic Geometry, George B Thom as and R oss L Finney , PEARSON Education, 9th Edition.
Differential and Integral Calculus, N, P iskunov , Volume-1 and Volume-2, CBS Publishers and distributors, India.
Differential Equations with applications and Historical notes, George F. Sim m ons and John S. R obertson , Tata
McGraw-Hill Publishing Company Limited, New Delhi, India.
Advanced Engineering Mathematics, Erw in K reyszig , John Wiley & Sons, Eighth Edition.
Advanced Engineering Mathematics, R K Jain, S R K I yengar , Third Edition, Narosa.
Engineering Mathematics, P eter V Onil, Tata McGraw Hill, New Delhi, India.
Note: P lease follow the topics from the follow ing specifications.
Sl No
Topic
Book to be followed
Differential calculus and Integral calculus
of single variable
Diff., Calculus by Shantinarayan, Diff, Int. Calculus by Piskunov,
Engineering mathematics by Jain and Iyengar.
Calculus of Several variables
Diff. Calculus by Shantinarayan, Calculus by Thomas, Finney,
Engg. math by Jain, Iyenger, Diff. Cal by Piskunov.
Multiple Integral and Vector Calculus
Int. Calculus by Thomas, Finney, Engg. M by Kreyszig, Engg. Jain
& Iyengar
Ordinary Differential Equations
Int. Calculus by Shantinarayan, Diff Eqns by G F Simmons, Engg.
M by Kreyszig, Jain & Iyengar
Syllabus of Mathematics-1 IIT Bhubaneswar
Calculus of Several Variables by S Pani.
The single variable calculus is a fascinating branch of
mathematics. We observe the wide range of problems that can
be dealt in this theory.
Functions with two or more independent variables appear more
often in science than functions of a single variable.
Now we explore what concepts can directly be translated to
functions of several variables. Does the limit continuity and
derivative as such translated to more than one variable calculus
or something else happens there? Nature is closure to more than
one variable calculus. Their calculus is even more interesting and
richer than the single variable calculus.
5
Calculus of Several Variables
Examples, Definition, Limit Continuity
Example 1. The area S of a rectangle with sides of length x and y is
expressed by the formula S=xy.
Example 2. The volume V of a rectangular parallelepiped with edges of
length x, y, z is expressed by the formula V =xyz.
Example 3. The range R of a shell fired with initial velocity v0 from a gun
whose barrel is inclined to the horizon at an angle is expressed by the
v sin 2
=
R
.
formula
g
2
0
Air resistance is disregarded and g is the acceleration of gravity.
Example 4. The volume of a right circular cylinder is a function of its
=
V f=
(r , h) r 2 h.
radius and height and we write it as
Calculus of Several Variables
Examples, Definition, Limit Continuity
We define a function of several variables as functions of n input variables
(as n number of independent real numbers) that yields a real number.
Definition: Suppose D is a set of n-tuples of real numbers (x1, x2,, xn). A
real valued function f on D is a rule that assigns a real number w = f(x1 , x2 ,
, xn) to each element in D.
The set D is the functions domain. The set of w values taken on by f is
the function's range. w is the dependent variable and x1 , x2, , xn are
independent variables.
Note: The largest set for which the function f is defined is known as the
natural domain of the function. As in f(x,y) = log (x2 + y2 -1), the domain is
not the entire plane, rather it is R2 - { (x, y) | x2 + y2 1 0}.
7
Calculus of Several Variables
Domain, Range, Level curve, Contour line
Example 1. If f(x,y,z) = xy log (z), the domain is the half space z>0, and
range is (- , ).
Definition. The set of points in the plane where the function f(x, y) has a
constant value i.e. f(x, y)=c is called a level curve of f.
Definition. The set of all points (x, y, f(x,y)) in the space for (x, y) in the
domain of f is called the graph of f. The graph of f is also called the
surface z=f(x, y).
Definition. The curve in space in which the plane z=c cuts a surface
z=f(x, y) is made up of the points that represent the function value f(x, y)=c.
This is called the contour line.
This is on the surface, its corresponding level curve is on the xy-plane.
Definition. The set of points (x, y, z) in space where a function of three
independent variables has a constant value that is f(x, y, z)=c is called a
level surface of f.
Calculus of Several Variables
Examples, Level curve and Contour Line
Calculus of Several Variables
Interior, point, boundary point, Boundary of a set,
Closed Ball, Open Ball, Open set, closed set, etc.
The distance notion is generalized to the concept of metrics and open sets closed sets and
continuity are expressed in terms of the concept of metric spaces.
Definition. A metric space is a set X with a distance function d:XXR,
satisfying the following properties:
(M1) d(x, y) 0, for all x, y (x y) X, (non negativity) and d(x, x)=0, for all x X,
(M2) d(x, y) = d(y, x), (symmetry),
(M3) d(x, y) d(x, z)+ d(z, y), for all x, y, z X (triangle inequality).
Examples. 1. Let X= R with d(x,y) = |x-y|, is a metric space, known as the
standard metric on R. 2. X = RR with d(x, y) = ( x1 y1 )2 + (x 2 y2 )2
, where
x=(x1,x2), y = (y1,y2), is a metric space, known as the standard metric on R2.
Definition. A neighbourhood of a point x in X is the set of all points y in X
such that, d ( x, y ) < .
Sometimes this neighbourhood is called -neighbourhood of x.
10
Calculus of Several Variables
Interior, point, boundary point, Boundary of a set,
Closed Ball, Open Ball, Open set, closed set, etc.
Definition. A point (x0, y0) in a region R in the xy-plane is called an interior
point of R if it is a center of a disk that lies entirely in R. A point (x0, y0) is a
boundary point of R if every disk centered at (x0, y0) contains points that
lie outside of R as well as points that lie in R. The boundary point need not
belong to R.
Definition. The interior of region R is the set of interior points of region R.
The regions boundary points make up its boundary.
Definition. A region is open if it consists entirely of interior points. A region
is closed if it contains all of its boundary points.
Definition. A region in the plane is bounded if it lies inside a disk of fixed
radius. A region is unbounded if it is not bounded.
In fact closed set, open set are the basic sets follows from the metric spaces
(generalization of the distance function). Then continuity is expressed in terms of open
sets and such sets plays important roll in higher mathematics.
11
Mathematics-1, Calculus of Several Variables
Limit of functions f:R2R
Definition: We say that a function f(x, y) approaches the limit L as (x,y)
approaches (x0, y0), and write
lim
( x , y ) ( x0 , y0 )
f (x, y) = L
, if for every >0
there exists a corresponding number > 0 such that for all (x, y) in the
domain of f,
0 < ( x x0 ) 2 + ( y y0 ) 2 <
| f ( x, y ) L |< .
The - requirement is also equivalent to: to given >0, there exists a
corresponding > 0 such that
0 <| x x0 |< and 0 <| y y0 |< | f ( x, y ) L |< .
Since more than one variable is involved in this case, finding the limit is more
technical, and one has to take care how the variables interact among themselves
and conclude about the limit.
12
Calculus of Several Variables
Limit for three Variables
Definition: We say that a function f(x, y, z) approaches the limit L as
lim
f (x, y, z) = L , if for
(x,y,z) approaches (x0, y0, z0), and write ( x , y , z )
( x0 , y0 ,z0 )
every >0 there exists a corresponding number > 0 such that for all (x,
y,z) in the domain of f,
0 < ( x x0 ) 2 + ( y y0 ) 2 + ( z z0 ) 2 <
| f ( x, y, z ) L |< .
The - requirement is also equivalent to: to given >0, there exists a
corresponding > 0 such that
0 <| x x0 |< , 0 <| y y0 |< , and 0 <| z z0 |< | f ( x, y, z ) L |< .
Similarly this definition can be extended to n number of variables.
Now we learn the techniques to conclude if the limit does not exist.
13
Calculus of Several Variables
Properties of Limits:
Theorem 1: If
(i)
(ii)
(iii)
(iv)
(v)
lim
( x , y ) ( x0 , y0 )
f (x, y) = L,
and
lim
( x , y ) ( x0 , y0 )
g (x, y) = M ,
then
[ f (x, y) g(x, y)] =
L M , (sum and difference rule)
lim
( x , y ) ( x0 , y0 )
[ f (x, y).g(x, y)] = L.M , (product rule)
lim
( x , y ) ( x0 , y0 )
lim
[ f (x, y) =
/ g(x, y)] L / M ( M 0), (quotient rule)
lim
[c f (x,
y)] cL, c , (c a constant, constant multiple rule)
=
( x , y ) ( x0 , y0 )
( x , y ) ( x0 , y0 )
lim
[ f (x, y)]m / n = Lm / n , (power rule, provided Lm / n is areal number)
( x , y ) ( x0 , y0 )
These rules look is very simple and innocent but very powerful and really serves us
in our difficulty. More useful to engineers than to mathematicians.
14
Calculus of Several Variables
Existence and Non-existence of limit, working procedure.
1. Repeated Limits: lim lim f ( x, y )
x a
y b
and
lim lim f ( x, y )
y b x a
Are known as repeated limits. If both the limits exists and equal then the
double limit exists, i.e.
lim
( x , y ) (a,b)
f ( x, y ) exists. If repeated limit differs, then
we conclude that the limit does not exist.
Path Test: If for all function y=(x) such that (x) b as xa, the limit
lim f ( x, ( x)) exists and is unique, then we have
x a
lim
( x , y ) (a,b)
f (x, y) = lim f ( x, ( x)).
x a
If along two such functions(y=1(x), y=2(x) ) or two such paths the limit differs
then we conclude that the limit does not exist.
15
Calculus of Several Variables
Existence and Non-existence of limit, working procedure.
1. Most powerful method is - method. If we can establish the proof of
existence of limit by this method then it is done, nothing else is required.
2. In case we doubt that the limit does not exist then we take the help of
repeated Limits, choosing different paths, etc. But these test does not
confirm about the existence of the limit.
x+ y
Example: Find the limits
(i ) lim
,
( x , y ) (0,0) 2 x y
x2 x y
(iii ) lim
,
2
( x , y ) (0,0)
x +y
xy 3
(ii ) lim
,
( x , y ) (0,0) x 2 + y 6
x3 y 3
(iv) lim cos 2
.
2
( x , y ) (0,0)
x +y
16
Examples(Verification of the limit by - definition):
Example 1. If (x,y) = y/(x2 + 1), then
lim
( x , y ) (0,0)
y)
=
f (x,
0
= 0.
0 +1
Let > 0 be a given number. Then |(x,y) 0|=| y/(x2 + 1)-0|=| y/(x2 + 1)|=
| y| / |(x2 + 1)| | y | < . Then | (x,y) - 0 | | y | < = .
Hence, we have found > 0 such that 0 <| x-0|< and 0<|y-0|<
|(x,y) - 0| < , which establishes the limit.
f ( x, y)
=
Example 2. If
xy
We have
=
0
x2 + y 2
xy
=
, then lim f (x, y) 0.
2
2
( x , y ) (0,0)
x +y
1 x2 + y 2
1 2
x2 + y 2
2
<
=
x + y < . Using |xy|
.
2 x2 + y 2 2
2
x2 + y 2
xy
Now choosing < 2 , we get
xy
x +y
2
0 < whenever 0< x 2 + y 2 < .
Which establishes the limit.
17
Calculus of Several Variables
Limit(Changing to Polar Coordinate (when (x,y)(0,0))
Substitute x=r cos , y=r sin , in f(x, y), let the resulting function be F(r, ),
then investigate the limit of the resulting expression as r0. Equivalently:
for every >0 there exists a corresponding number > 0 such that for all
r and , we have
| r |<
| F(r , ) L |< .
=
lim f( x, y ) lim
=
F (r , ) L.
If such L exists then
Example: Find
( x , y ) (0,0)
r 0
x3
lim f( x, y ) if f ( x, y ) = 2
.
( x , y ) (0,0)
x + y2
We have
x3
r 3 cos3
lim
lim
r cos3 0.
= lim=
=
2
( x , y ) (0,0) x 2 + y 2
r 0
r
0
Example: Find
lim f( x, y ) if f ( x, y ) =
( x , y ) (0,0)
x2
lim
=
( x , y ) (0,0) x 2 + y 2
r 2 cos 2
lim
=
r 0
r2
lim
We have,
r 0
thus we conclude that the limit does not exist.
x2
.
x2 + y 2
cos 2 .
But cos2 , takes all values in [0,1],
18
Calculus of Several Variables
Limit(Some times Polar conversion takes us to false conclusion)
Example: Find
2x2 y
lim f( x, y ) if f ( x, y ) = 4
.
( x , y ) (0,0)
x + y2
Solution: Changing it to polar coordinates we get
lim
( x , y ) (0,0)
2x2 y
x4 + y 2
2r 3 cos 2 sin
r cos sin 2
lim =
lim
0.
=
r 0
r 0
r 4 cos 4 + r 2 sin 2
r 2 cos 2 + sin 2
Taking the limits
along y=mx2, we
could easily see
that the limit does
not exist.
Holding constant and r0, we have limit as 0.
on the path y=x2, that is rsin =r2 cos2 , we have
2x2 y
lim
=
( x , y ) (0,0) x 4 + y 2
2x2 x2
lim
lim
=
( x , y ) (0,0) x 4 + x 4
r 0
2r 4 cos 2 cos 2
= 1.
r 4 cos 4 + r 4 cos 4
Thus on a different path we get a different limit and we conclude that the limit does not
exists. This also we can see in the form of Cartesian coordinates.
W e have to be m ore careful in w orking out the problem s.
19
Calculus of Several Variables
Continuity of functions (two independent variables)
Definition: We say that a function f(x, y) is continuous at a point (x0, y0),
if for every >0 there exists a corresponding number > 0 such that for
all (x, y) in the domain of f, satisfying
0 < ( x x0 ) 2 + ( y y0 ) 2 <
| f ( x, y ) f ( x0 , y0 ) |< .
In other words with the help of metric notation continuity can be written
as: a function f(x, y) is continuous at a point (x0, y0), if for every >0, there
exists a corresponding > 0 such that
0 < d ( ( x, y ), ( x0 , y0 ) ) < | f ( x, y ) f ( x0 , y0 ) |< .
In higher mathematics continuity is expressed in terms of this metric notation or the most
generalized way that f is continuous if it brings back open sets to open sets. (If f:XY, where X, Y
are topological spaces then f is continuous if for every U a open set in Y, then f-1(U) is open in X.)
20
Calculus of Several Variables
Continuity of functions (three independent variables)
Definition: We say that a function f(x, y, z) is continuous (x0, y0, z0), if
for every >0 there exists a corresponding number > 0 such that for all
(x, y) in the domain of f, satisfying
0 < ( x x0 ) 2 + ( y y0 ) 2 + ( z z0 ) 2 <
| f ( x, y, z ) f ( x0 , y0 , z0 ) |< .
The definition is similar for n-independent variables.
In other words with the help of metric notation continuity can be written
as: to given >0, there exists a corresponding > 0 such that
0 < d ( ( x, y, z ), ( x0 , y0 , z 0 ) ) < | f ( x, y, z ) f ( x0 , y0 , z 0 ) |< .
With this metric concept this definition of continuity can be generalized even to function
spaces, where the domain is not Rn, but its members are all function (say C[a, b]). Useful
concept for the analysis of differential equations, integral equations, etc.
21
Calculus of Several Variables
Continuity of functions (Limit concept)
Definition: A function (x,y) is continuous at the point (x0,y0) if
1. is defined at (x0,y0).
2. lim (x,y)(x0,y0) (x,y) exists.
3. lim (x,y)(x0,y0) (x,y) = (x0,y0).
This definition is useful to work out the problems. This is equivalent to
the - definition given earlier.
A function is continuous if it is continuous at every point of its domain. From
Theorem 1 the sums, differences, products, constant multiples, quotients and
powers of continuous functions are continuous wherever defined. Polynomials and
rational functions of two variables are continuous at every point at which they are
defined.
If z = (x,y) is a continuous function of x and y, and w = g(z) is a
continuous function of z, then the composite w= g((x,y)) is continuous.
Thus ex-y and ln (1 + x2y2) are continuous at every point (x,y).
22
Calculus of Several Variables
Partial Derivatives (Derivative has some difficulty)
Definition: We define the partial derivative of (x, y) with respect to x at
(x0,y0) as the ordinary derivative of (x,y0) with respect to x at x=x0.
The partial derivative of (x,y) with respect to x at (x0,y0) is :
f ( x0 + h, y0 ) f ( x0 , y0 )
f
d
= =
f ( x, y0 )
lim
.
h 0
x ( x0 , y0 ) dx
h
x = x0
The plane y=y0 will cut the surface z= (x,y) in the curve z= (x,y0). The
slope of the curve z=(x,y0) at (x0 ,y0, (x0,y0)) is /x |(x0, y0) .
The notation for a partial derivative: Partial derivative of f(x, y) at (x0,y0)
with respect to x is denoted by f (x 0 , y0 ), or f x ( x0 , y0 ).
x
Simply by /x or x we mean Partial derivative of with respect to x.
Exactly in a similar way we define the partial derivative with respect to y.
23
Calculus of Several Variables
Partial Derivatives (Derivative has some difficulty)
Definition: We define the partial derivative of (x,y) with respect to y at
(x0,y0) as the ordinary derivative of (x0,y) with respect to y at y=y0.
The partial derivative of (x,y) with respect to y at (x0,y0) is :
f ( x0 , y0 + k ) f ( x0 , y0 )
f
d
= =
f ( x0 , y )
lim
.
k 0
y ( x , y ) dy
k
y= y
0
The plane x=x0 will cut the surface z= (x,y) in the curve z= (x0,y). The
slope of the curve z=(x0,y) at (x0 ,y0, (x0,y0)) is /y |(x0, y0) .
The notation for a partial derivative: Partial derivative of f(x, y) at (x0,y0)
with respect to y is denoted by f (x 0 , y0 ), or f y ( x0 , y0 ).
y
Simply by /y or y we mean Partial derivative of with respect to y.
Exactly in a similar way we define the partial derivative for more than two
24
variables.
Calculus of Several Variables
Partial Derivatives (Examples)
Example 1: Find the values of /x and /y at the point (4 , -5) if
(x,y) = x2 + 3xy + y 1.
Solution: /x = /x(x2 + 3xy + y 1) = 2x + 31 y+00 = 2x + 3y.
The value of /x at (4, -5) is
2(4) + 3(-5) = -7
We have /y = /y (x2 + 3xy + y 1) =0+3 x1+10 =3x +1.
Thus the value of /y at (4, -5) is 3(4) + 1 = 13.
Example 2: Find /y if (x,y) = y sin xy.
Solution: /y = /y(y sin xy) = y /y sin xy + (sin xy) /y (y)=xy cos
xy + sin xy.
Example 3: The plane y= 1 intersects the paraboloid z = x2 + y2 in a parabola.
Find the slope of the tangent to the parabola at (2, 1, 5).
Solution: The slope is the value of the partial derivative z/x at (2, 1), that is
z/x |(2, 1) = /x (x2 + y2) |(2, 1) =2 x |(2, 1) = 2 (2) = 4.
25
Calculus of Several Variables
Partial Derivatives(Functions of more than Two variables )
Example 1: If x , y and z are independent variables and w = (x, y, z) = x
sin(y + 3z). Then find all the partial derivatives.
Solution: We have /z = /z [x sin(y + 3z)] = x /z sin (y + 3z)
= x cos(y + 3z ) /z (y + 3z) = 3x cos (y + 3z).
Second Order Partial Derivatives:
2 f
f
=
f xx =
,
2
x
x x
2 f
f
=
f yy =
.
2
y
y y
Mixed Partial Derivatives
2 f
f
2 f
f
=
=
=
f xy =
f
,
yx
.
xy x y
yx y x
These mixed derivatives fxy and fyx are not always equal. But in real life applications we find
them equal. Under what conditions they are equal is given by Eulers Theorem.
26
Calculus of Several Variables
Eulers Theorem(Equality of mixed derivatives fxy=fyx)
The Mixed Derivative Theorem: If (x,y) and its partial derivatives x , y , xy , yx
are defined throughout an open region containing a point (a, b) and are all continuous at (a,
b), then xy(a,b) = yx(a,b). Some times it is known as Shcwartz Theorem.
Youngs Theorem: If (x,y) and its partial derivatives x , y
exists in a certain
neighborhood of (a, b) and if both are differentiable at (a,b) then xy(a,b) = yx(a,b).
Example: Find 2w/x y if
w = x y + ey / (y2 + 1 ).
and
2w/y x = 1. We are in for more work if we
Solution: w/x = y
differentiate with respect to y first.
Example: Compute Mixed partial derivatives from first principle and show that
they are not equal for
xy ( x 2 y 2 )
, ( x, y ) (0, 0)
f ( x, y ) = x 2 + y 2
0,
( x, y ) = (0, 0).
Solution: Computing from first principle we get:
f xy (0, 0) =
1, f yx (0, 0) =
1
f xy f yx .
27
Calculus of Several Variables
Eulers Theorem(Homogeneous Functions)
Definition: A function f(x,y) is said to be hom ogeneous function of
degree n, if f(tx,ty)=tnf(x,y), for all positive values of t. Similarly a function in
n variables is said to be homogenous function of degree p if
f (tx1 , tx2 , tx3 , , txn ) = t p f ( x1 , x2 , x3 , , xn ).
Eulers Theorem of First Order(Two Variables):
If function f(x,y) is a homogeneous function of degree n, then
x
f
f
+y
=
nf ( x, y ).
x
y
Proof: The homogeneous function f(x, y) can be expressed as f(x, y)
=xng(y/x). Then
and
f ( x n g ( y / x))
1
n 1
n
=
x
= nx
x
f ( x n g ( y / x))
x
=
= x n g '( y / x) 2 .
y
y
y
x
f
f
+=
y
x
y
xnx n 1 g ( y / x ) + xx n g '( y / x )
g ( y / x) + x g '( y / x) .
y
Then
1
x
yx n g '( y / x=
) 2
y
y
nx n g ( y=
/ x)
nf ( x, y ).
28
Calculus of Several Variables
Eulers Theorem(Homogeneous Functions)
Eulers Theorem of Second Order (Two Variables): If function f(x,y) is a
homogeneous function of degree n, then
2
2 f
2 f
2 f
x
+ 2 xy
+y
=
n(n 1) f ( x, y ).
x 2
xy
y 2
2
Proof: The homogeneous function f(x,y) can be expressed as f(x,y)
=xng(y/x). Computing the second order partial derivatives and simplifying
we get this result. Using the first order and second order results we can solve some
problems easily as in these examples:
3
3
+
x
y
1
Example:
If u ( x, y ) tan
=
, x y, then show that
x y
u
u
=
(i ) x + y
sin 2u , and
x
y
2
2u
2u
2 u
+ 2 xy
+y
=
(ii ) x
(1 4sin 2 u) sin 2u.
2
2
x
xy
y
2
29
Calculus of Several Variables
Eulers Theorem(Homogeneous Functions)
Solution: Here u is not a homogeneous function but if we write
3
x3 + y 3
2 1 + ( y / x)
z tan
u
, x y.
=
=
= x
x y
1 ( y / x)
z is a homogeneous function of x, y of degree 2. Thus we can apply Eulers theorem to z and
we have:
z
z
z
z z
z
2
and
+y
=
2 z, =
sec
=
u ,
sec 2 u
x
y
x
x y
y
xux+yuy=2z we get
using these equations in
u
u
u
u 2 tan u
= 2 =sin 2u.
sec 2 u x + y =2 z =2 tan u x + y
x
y
x
y
sec u
2
2
u
u
2
2
For the second part calculate
=
sec
u
+
2sec
u
tan
u
.
2
2
x
x
x
2
Similarly
calculating other terms and putting in the Eulers 2nd order Theorem and simplifying we
get the desired result. Try self.
30
Calculus of Several Variables
Differentiability (Functions of Two variables )
Here the idea of Fermats quotient fails for differentiability because the denominator we
do not have a real number to perform the division thus instead of that we seek it via
increment concept that is useful for us.
A function (x,y) is differentiable at (x0,y0) if x(x0,y0) and y(x0,y0)
exist and the following equation holds for at (x0,y0):
f=
( x, y ) f ( x0 , y0 ) + f x ( x0 , y0 )( x x0 ) + f y ( x0 , y0 )( y y0 ) + 1x + 2 y.
where 1, 2 0 as x, y 0.
If the increments x and y are small, then the products 1 x and 2 y
will be smaller and we will have
(x,y) (x0, y0) + x(x0, y0) (x-x0) + fy(x0, y0) (y-y0).
or,
(x,y) L(x, y),
where, L(x,y)= (x0, y0) + x(x0, y0) (x-x0) + fy(x0, y0) (y-y0) ) is the linear
approximation of the function.
31
Calculus of Several Variables
Differentiability (Functions of Two variables )
How do we get this expression?
f=
( x, y ) f ( x0 , y0 ) + f x ( x0 , y0 )( x x0 ) + f y ( x0 , y0 )( y y0 ) + 1x + 2 y.
Suppose z = (x,y) and (x0,y0), (x0 +x, y0+y) be any two points so that
x and y are the changes in the independent variables x and y. Let z be
the consequent change in z. Thus z+z=f (x0 +x, y0+y). We proceed as
follows:
z= ( z + z ) z= f ( x + x, y + y ) f ( x, y )
= f ( x + x, y + y ) f ( x + x, y ) + f ( x + x, y ) f ( x, y ).
By Lagranges mean value theorem we can write
f ( x + x, y + y ) f ( x + x, y ) = y f y ( x + x, y + 1y ), and
f ( x + x, y ) f ( x, y ) = x f x ( x + 2 x, y ).
Further we can write
f y ( x + x, y +=
1y ) f y ( x, y ) + 2 , and f x ( x + 2=
x, y ) f x ( x, y ) + 1.
32
Calculus of Several Variables
Differentiability (Functions of Two variables )
Thus we have: z = z + z z = f ( x + x, y + y ) f ( x, y )
= f ( x + x, y + y ) f ( x + x, y ) + f ( x + x, y ) f ( x, y )
= y f y ( x + x, y + 1y ) + x f x ( x + 2 x, y )
= y f y ( x, y ) + x f x ( x, y ) + 1x + 2 y.
Equivalently we have
f=
( x, y ) f ( x0 , y0 ) + f x ( x0 , y0 )( x x0 ) + f y ( x0 , y0 )( y y0 ) + 1x + 2 y.
We are assuming the required assumptions for Lagranges theorem and
continuity of fx and fy, where ever necessary. 1 0, and 2 0 as x 0 and
y 0 we have
z
z
z=
x +
y.
x
y
z
z
dz
dx
dy.
=
+
Further as x 0 and y 0 we can write
x
y
33
Calculus of Several Variables
Differentiability (Functions of Two variables )
Thus we have the definition as:
Definition: A function (x,y) is differentiable at (x0,y0) if x(x0,y0) and y(x0,y0)
exist and the following equation holds for at (x0,y0):
z = x f x ( x, y ) + y f y ( x, y ) + 1x + 2 y.
where 1, 2 0 as x, y 0.
Definition: If a function (x,y) is differentiable and we move from a point (x0,y0) to
a point (x0+dx,y0+dy) in its neighborhood then the resulting differential in f is
dz =df = f ( x + dx, y + dy ) f ( x, y ) = f x ( x0 , y0 )dx + f y ( x0 , y0 )dy.
This is called as the total differential of f.
Relation between continuity and the existence of partial derivatives:
A function (x,y) can have partial derivatives with respect to both x and y at a point
without being continuous there at. For example the function f(x,y)=0, xy0, 1 if
xy=0. Then fx and fy exists at (0,0) but the function is not continuous at (0,0).
34
Calculus of Several Variables
Linearization (Or Linear Approximation of a function of two variables )
From this we provide the definition as
Definition (Linearization) The linearization of a function (x,y) at a point
(x0,y0) where is differentiable is the function
L(x,y) = (x0, y0) + x(x0, y0) (x-x0) + fy(x0, y0) (y-y0).
The approx im ation (x ,y) L(x ,y) is the standard linear approx im ation of at (x 0 , y 0 ).
Example 1: Find the linearization of (x,y) = x2 xy + y2 + 3 at the point (3,2).
Solution: We calculate the following terms
(x0, y0) = (x2 xy + y2 + 3)(3,2) = 8,
x (x0, y0) = /x (x2 xy + y2 + 3)(3,2) = (2x y)(3,2) = 4,
putting in,
y (x0, y0) = /y (x2 xy + y2 + 3)(3,2) = (-x + y)(3,2) = -1,
L(x,y) = (x0, y0) + x (x0, y0) (x - x0) + y (x0, y0) (y - y0)
= 8 + (4) (x 3) + (-1)(y 2) = 4x y 2.
Thus the linearization of at (3,2) is L(x,y) = 4x y 2.
35
Calculus of Several Variables
Linearization (Or Linear Approximation of a function of three variables )
Definition (Linearization) The linearization of a function (x,y,z) at a point
p0(x0,y0,z0) where is differentiable is the function
L(x,y,z) = (p0) + x (p0) (x - x0) + y (p0) (y - y0) + z (p0) (z - z0).
The approx im ation (x ,y) L(x ,y) is the standard linear approx im ation of at (x 0 , y 0 , z 0 ).
Example 1: Find the linearization L(x,y,z) of f(x,y,z) = x2 xy+3 sinz at the point p0(2, 1, 0).
Solution: Calculating we get (p0) = 2, x (p0) = 3,
y (p0) = -2,
z (p0) = 3 .
Thus the linearization is L(x,y,z) = 2 + 3 (x-2) + (-2) (y-1) + 3 (z-0) = 3x 2y + 3z 2.
Definition (Total differential)
If we move from (x0, y0, z0) to a point (x0+dx, y0+dy, z+dz), the resulting differential
in is d = x(x0,y0,z0) dx + y(x0,y0,z0) dy+z(x0,y0,z0) dz
This change is called the total differential of .
36
Mathematics-1, Calculus of Several Variables
Chain Rule (Functions of Two Independent Variables)
Theorem: If w= (x,y) is differentiable and x and y are differentiable functions of t,
then w is a differentiable function of t and
dw/dt = /x . dx/dt + /y . dy/dt
w = (x,y)
w/x
(1)
Dependent variable
w/y
.y Intermediate
variables
dy/dt
dx/dt
Independent variable
dw/dt = w/x . dx/dt + w/y . dy/dt
37
Mathematics-1, Calculus of Several Variables
Chain Rule and Implicit Differentiation
Example: Use the Chain Rule to find the derivative of w = xy with respect to t along the
path x = cost, y = sint. What is the derivatives value at t = / 2 ?
Solution: w/x = y = sin t, w/y = x = cos t, dx/dt = -sin t, dy/dt = cos t and
dw/dt = w/x . dx/dt + w/y . dy/dt
= -sin2 t + cos2 t = cos 2t.
(sin t) (-sin t) + (cos t) (cos t)
Differentiation of Implicit Functions (Finding dy/dx when f(x, y)=0):
We consider a function f of two variables x and y, where y is not explicitly given in terms of x
but f(x, y)=0. Note that f is a function of x and y and also y is a function of x. Thus
df f dx f dy
dw f dx f dy
=
=
. + .
, using
. + . ,
dx x dx y dx
dt x dt y dt
=
w f ( x,=
y ), x x=
where
(t ), y y (t ).
But given f(x,y)=0, thus we have
f
df
f f dy
dy
f / x
=
+ . =
=
=
x.
0
0
dx
x y dx
dx
f / y
fy
38
Mathematics-1, Calculus of Several Variables
Chain Rule and Implicit Differentiation
Differentiation of Implicit Functions (Finding d2y/dx2 when f(x,y)=0):
Using dy/dx we proceed as follows:
f
f
fx )
(
( fy )
2
fx
f / x
dy
d y
y x
x x
=
2
f / y
dx
fy
dx 2
f
y
f 2 f dy 2 f f 2 f
2 f dy
+
+
y yx dx x 2 x xy y 2 dx
=
2
f
y
Further simplifying we get
fx
fx
f y f yx
+ f xx f x f xy +
f yy
fy
fy
d2y
=
2
2
dx
(f )
y
f y ( f yx ( f x ) + f y f xx ) f y f x ( f xy f x f yy )
( f y ) 2 f xx 2 f y f yx f x + f yy ( f x )
.
=
3
3
( fy )
( fy )
39
2
Mathematics-1, Calculus of Several Variables
Chain Rule and Implicit Differentiation
Example: Find dz/dt if z= xy2+x2y, x=at2, y=2at.
Solution: Calculating we get z/x= y2+2xy, z/y= 2xy+x2, dx/dt=2at, dy/dt=2a, using the chain rule
we get z/t = a3(16t3+10t4).
dz z dx z dy
=
. + . ,
dt x dt y dt
d 2 y 2a 2 x 2
3
2
3
Problems (1): Find dy/dx and prove that
+
=
0,
if
y
3
ax
=
+
x
0.
2
5
dx
y
dy
y
f ' x y + x
(2) If xyf(y/x)=a, where a is a constant, then show that
dx
x=
.
y
dy
f
y y x
dx
x
(3) If f(x,y)=0, then prove that
2 f
2 f dy 2 f dy
f d 2 y
+2
+
=
0.
+
x 2
xy dx dy 2 dx
y dx 2
2
40
Mathematics-1, Calculus of Several Variables
Chain Rule (for Three Independent Variables)
If w = (x,y,z) is differentiable and x, y and z are differentiable functions of t, then w is
dw f dx f dy f dz
a differentiable function of t and
dx/dt
w/z
w/y
dy/dt
dt x dt y dt z dt
Dependent Variable
w = (x,y,z)
w/x
.z
.y
dz/dt
Intermediate Variables
Independent Variable
dw/dt = w/x . dx/dt + w/y . dy/dt + w/z . dz/dt
41
Mathematics-1, Calculus of Several Variables
Chain Rule (for n-Independent Variables)
If w = (x1,x2,,xn) is differentiable and x1, x2, , xn are differentiable functions of t,
then w is a differentiable function of t and
dw f dx1 f dx2
f dxn
.
.
.
.
=
+
+ +
dt x1 dt x2 dt
xn dt
Theorem: If w = (x,y) is differentiable function and x and y are differentiable
functions of u and v, then w is a differentiable function of u and v, i.e. if
=
w f=
( x, y ), x (u, v),=
and y (u , v).
Then
dw w x w x
dw w x w x
=
. +
.
and
=
. +
. .
du x u x u
dv x v x v
Example: Find dz/dt if z= xy2+x2y, x=at2, y=2at.
Solution: Calculating we get z/x= y2+2xy, z/y= 2xy+x2, dx/dt=2at, dy/dt=2a,
dz z dx z dy
using the chain rule
we get z/t = a3(16t3+10t4).
=
. + . ,
dt
x dt
y dt
42
Mathematics-1, Calculus of Several Variables
Problems on Chain Rules
Solve the following problems:
1. If u = (y-z, z-x, x-y), then prove that
2. If
u =
x
+ y2 + z2
u u u
+
+
=
0.
x y z
then show that u xx + u yy + u zz =
0.
3. If u = (x2+2yz, y2+2xz), then prove that
u
u
u
2
2
( y zx) + ( x yz ) + ( z xy )
=
0.
x
y
z
2
4. If z = xm(y/x)+xng(x/y), then prove that
2
z
2 z
2 z
z
2 z
+
+
+
=
+
+
x
2
xy
y
mnz
(
m
n
1)
x
y
.
x 2
xy
y 2
y
x
2
5. If
=
u
log( x 3 + y 3 + z 3 3 xyz ),
then show that
9
+
+
=
u
.
+
+
x
y
z
(
x
y
z
)
43
Mathematics-1, Calculus of Several Variables
Taylors Theorem for a Function of two variables
(with remainder after three terms only)
Theorem: If possesses continuous partial derivatives of the third order in a
neighborhood of a point (a, b) and if (a+h, b+k) be a neighborhood point of (a,b), then
there exists a (0< <1) such that
f (a + h, b +=
k)
+
f (a, b) + hf x (a, b) + kf y (a, b) +
1 2
h f xx (a, b) + 2hkf xy (a, b) + k 2 f yy (a, b)
2!
1 3
h f xxx (a + h, b + k ) + 3h 2 kf xxy (a + h, b + k ) + 3hk 2 f xyy (a + h, b + k ) + k 3 f yyy (a + h, b + k )
3!
Proof: We write z=f(x,y) and x=a+ht, y=b+kt. Then z is a function of t, we can write
z=g(t) =f(x,y). Now we have
=
g '(t ) f x ( x, y )
dx
dy
+ f y ( x, y ) .
dt
dt
dx
dy
dx
dy
g ''(t ) = h f xx ( x, y ) + f yx ( x, y ) + k f xy ( x, y ) + f yy ( x, y )
dt
dt
dt
dt
=h 2 f xx ( x, y ) + 2hkf xy ( x, y ) + k 2 f yy ( x, y ).
44
Mathematics-1, Calculus of Several Variables
Taylors Theorem for a Function of two variables
(with remainder after three terms only)
Similarly we have
g '''(t ) =h3 f xxx ( x, y ) + 3h 2 kf xxy ( x, y ) + 3hk 2 f xyy ( x, y ) + k 3 f yyy ( x, y ).
Maclaurins seres for g(x) is
g (t=
) g (0) + tg '(0) +
1 2
1
t g ''(0) + t 3 g '''( t), 0 < < 1.
2!
3!
Taking t=1 in this series we get
1
1
g (1)= g (0) + g '(0) + g ''(0) + g '''( ), 0 < < 1.
2!
3!
Substituting back we get:
f (a + h, b +=
k)
+
f (a, b) + hf x (a, b) + kf y (a, b) +
1 2
h f xx (a, b) + 2hkf xy (a, b) + k 2 f yy (a, b)
2!
1 3
h f xxx (a + h, b + k ) + 3h 2 kf xxy (a + h, b + k ) + 3hk 2 f xyy (a + h, b + k ) + k 3 f yyy (a + h, b + k )
3!
45
Mathematics-1, Calculus of Several Variables
Taylors Theorem for a Function of two variables
(with remainder after three terms only)
This expression can be written as:
f ( x,=
y)
f (a, b) + ( x a ) f x (a, b) + ( y b) f y (a, b)
+
1
( x a ) 2 f xx (a, b) + 2( x a )( y b) f xy (a, b) + ( y b) 2 f yy (a, b) +
2!
Further with differential operator notation this can be written as:
f ( x,=
y)
f ( a, b) + ( x a ) + ( y b) f ( a, b)
x
y
1
1
+ ( x a ) + ( y b) f ( a, b) + ( x a ) + ( y b) f ( a, b) +
x
y
x
y
2!
3!
Where the terms have
meaning as follows:
2
2
2
2
2
2
( x a ) x + ( y b) y f (a, b) = ( x a ) x 2 f (a, b) + 2( x a )( y b) xy f (a, b) + ( y b) y 2 f (a, b).
3
3
3
3 f
3 f
2
2 f
3
( x a ) x + ( y b) y f (a, b) = ( x a ) x 3 + 3( x a ) ( y b) x 2 y + 3( x a )( y b) xy 2 + ( y b) y 3
.
(a,b)
46
Mathematics-1, Calculus of Several Variables
Taylors Theorem for a Function of two variables
(with remainder after three terms only)
Example 1: Expand the function f(x,y) = x2+xy-y2 by Taylors theorem in powers of (x1) and (y+2).
Solution: The Taylors series is given by:
f ( x,=
y)
1
+ ( y b)
f ( a, b) + ( x a )
f ( a, b) + 2! ( x a ) x + ( y b) y
x
y
f ( a, b) +
Thus point (a,b) = (1, -2), and we calculate, f(1,-2)=5, f/x=2x+y, f/y= x-2y, etc,
putting the values we get
f ( a, b) +
( x a ) f x ( a, b) + ( y b) f y ( a, b)
1
( x a ) 2 f xx ( a, b) + 2( x a )( y b) f xy ( a, b) + ( y b) 2 f yy ( a, b)
+
+
2!
x 2 + xy y 2 =
5 + y + 2 + ( x 1) 2 + ( x 1)( y + 2) ( y + 2) 2 .
f ( x,=
y)
Problem 1: Expand the function f(x,y) = cos(x+y) by Taylors theorem about (0,0) up to
three terms.
Solution: The Taylors series is given by:
f ( x, y ) =cos( x + y ) =
1
1 2
1
x 2 xy + y 2 +
x 4 + 4 xy + 6 x 2 y 2 + 4 xy 3 + y 4 .
2
24
Problem 2: Obtain the Taylors series for the functions (i) f(x,y) = e2x+y (ii)f(x,y)
=xy2+ycos(x+y) about (1,0) and (1,1) up to three terms.
47
Mathematics-1, Calculus of Several Variables
Maxima Minima for a Function of two variables
(by Taylors Theorem )
Definitions: Let (x,y) be defined on a region R containing the point (a,b).Then
1. (a,b) is a local maximum value of (a,b) (x,y) for all domain points (x,y) in an
open disk centered at (a,b).
2.
(a,b) is a local minimum value of if (a,b) (x,y) for all domain points (x,y) in an
open disk centered at (a,b).
First Derivative Test for Local Extreme Values
If (x,y) has a local maximum or minimum value at an interior point (a,b) of its domain, and if
the first partial derivatives exist there , then x(x,y)=0 and y(x,y) = 0.
Proof: Suppose that has a local maximum value at an interior point (a,b) of its domain. Then
X = a is an interior point of the domain o the curve z = (x,b) in which the plane y = b cuts the surface z =
(x,y) in fig.
2.
The function z = (x,b) is a differentiable function of x at x = a (derivative is x(a,b)).
3.
The function z = (x,b) has a local maximum value at x = a.
4.
The value of the derivative of z = (x,b) at x = a is therefore zero (theorem 2, section 3.1) Since this derivative
is x(a,b), we conclude that x(a,b) = 0 .
A similar argument with the function z = (a,y) shows that y(a,b), = 0 .
This proves the theorem for local maximum values. The proof for local minimum values is similar.
1.
48
Mathematics-1, Calculus of Several Variables
Maxima Minima for a Function of two variables
(2nd derivative test by Taylors Theorem )
Definition: An interior point of the domain of a function (x,y) where both x and y are
zero or where one or both of x and y do not exist is a critical point of .
Definition: A differentiable function (x,y) has a saddle point at a critical point (a,b) if it in
every open disk centered at (a,b) there are domain points (x,y) where (x,y) > (a,b) and
domain points (x,y) where (x,y) < (a,b) .The corresponding point (a,b, (a,b)) on the surface
z = (x,y) is called a saddle point of the surface.
Second Derivative Test for Local Extreme Values
Suppose (x,y) and its first and second partial derivative are continuous throughout a disk
centered at (a,b) and that x(a,b) = y(a,b) = 0 .Then
1) has a local maximum at (a,b) if xx < 0 and xxyy - xy2 > 0 at
(a,b);
2
2) has a local minimum at (a,b) if xx > 0 and xxyy - xy > 0 at
(a,b);
2
3) has a saddle point at (a, b) if xxyy - xy < 0 at (a,b)
4)
The test is inconclusive at (a,b) if xxyy - xy2 = 0 at (a, b) . In this case, we must find
some other way to determine the behavior of at (a,b).
49
Mathematics-1, Calculus of Several Variables
2nd Derivative test by Taylors Theorem
Theorem: If possesses continuous partial derivatives of the third order in a
neighborhood of a point (a, b) and if (a+h, b+k) be a neighborhood point of (a,b), then
there exists a (0< <1) such that
f (a + h, b +=
k)
f (a, b) + hf x (a, b) + kf y (a, b) +
1 2
h f xx (a, b) + 2hkf xy (a, b) + k 2 f yy (a, b) +
2!
Proof: At a critical point the fx=0 and fy=0. Thus Taylors series reduces to
f (a + h, b +=
k)
f ( a, b) +
1 2
h f xx (a, b) + 2hkf xy (a, b) + k 2 f yy (a, b) +
2!
We rearrange the terms and get the expression as
f (a + h, b +=
k ) f ( a, b) +
= f ( a, b) +
1
h 2 f 2 xx + 2hkf xx f xy + k 2 f 2 xy k 2 f 2 xy + k 2 f xx f yy
+
( a ,b )
f xx (a, b)2!
1
(hf xx + kf xy ) 2 + k 2 ( f xx f yy f 2 xy ) .
f xx 2!
From this expression we get:
f ( a + h, b + k ) =
f ( a, b)
1
(hf xx + kf xy ) 2 + k 2 ( f xx f yy f 2 xy ) +
f xx 2!
50
Mathematics-1, Calculus of Several Variables
2nd Derivative test by Taylors Theorem
f ( a + h, b + k ) =
f ( a, b)
1
(hf xx + kf xy ) 2 + k 2 ( f xx f yy f 2 xy ) +
f xx 2!
Thus have the conclusion as follows:
if xx > 0 and xxyy - xy2 > 0 then the right side expression is positive quantity for
all values of h and k, thus (a,b) is a minimum point.
if xx < 0 and xxyy - xy2 > 0 then the right side expression is a negative quantity
for all values of h and k, thus (a,b) is a maximum point.
has a saddle point at (a, b) if xxyy - xy2 < 0 at (a,b), since depending upon h
and k the right side expression takes both positive and negative values.
) if xxyy - xy2 = 0 at (a, b), then the test is inconclusive and further investigation
is required.
For three variable case observe the difficulty level.
We leave it to you for investigation.
51
Mathematics-1, Calculus of Several Variables
Summary of the 2nd Derivative test of Max-Min
Summary of Max-Min Tests
The extreme values of (x,y) can occur only at
1. Boundary points of the domain of ,
2. Critical points (interior points where x = y = 0 or points where x or y fail to exist).
If the first and second order partial derivatives of are continuous throughout a disk
centered at point (a,b) , and x (a,b) = y (a,b) = 0, you may be able to classify (a,b) with
the second derivative test:
1) xx < 0 and xxyy - xy2 > 0 at (a,b)
Local Maximum,
2) xx > 0 and xxyy - xy2 > 0 at (a,b)
Local Minimum,
3) xxyy - xy2 < 0 at (a,b)
Saddle Point,
4) xxyy - xy2 = 0 at (a,b)
Test is inconclusive.
52
Mathematics-1, Calculus of Several Variables
Summary of the 2nd Derivative test of Max-Min
Problems of Max-Min.
1.
Find all the local maximum, minimum and saddle points of the functions
(i)
f(x,y) = x3y2(1-x-y),
(ii) f(x,y) = x3 + y3 63(x+y) +12xy,
(iii) f(x,y) = 4x2 6xy +5y2 -20x+26y,
(iv) xf(x,y) = 3y2- 2y3 -3x2+6xy.
2. Show that function f(x,y) = x2-2xy+y2+x4+y4 has a minimum at origin.
3. Find the absolute maxima, minima of the functions on the given domains.
(i)
f(x,y) = 2x2 -4x +y2-4y +1, on the closed triangular plate bounded by the lines x=0, y=2,
y=2x in the first quadrant.
(ii)
f(x,y) = x2 + xy + y2 6x, on the rectangular plane 0x5, 0y1.
(iii) f(x,y) = 4x-x2 cos y, on the rectangular plane 1x3, -/4 y /4.
4. Find two numbers a and b with a x b such that the following integral has its largest value.
(6 x x 2 )dx
53
CALCULUS OF SEVERL VARIABLES
========================
The End
Thank You
========================
54
Mathematics The Gem of all Sciences
========================
As are the crests on the heads of peacocks,
As are the gems on the hoods of cobras,
So is mathematics,
at the top of all sciences.
Yajurveda
55
Das könnte Ihnen auch gefallen
- Materi PolynomialDokument20 SeitenMateri PolynomialnormasulasaNoch keine Bewertungen
- Grammatical Categories of The VerbDokument26 SeitenGrammatical Categories of The Verbkopanica80% (5)
- Volumes of Solids of RevolutionDokument5 SeitenVolumes of Solids of RevolutionsergeNoch keine Bewertungen
- A-Level Further MathematicsDokument157 SeitenA-Level Further MathematicsShinichibi MenkemNoch keine Bewertungen
- Definite Integral (Calculus) Mathematics E-Book For Public ExamsVon EverandDefinite Integral (Calculus) Mathematics E-Book For Public ExamsBewertung: 4 von 5 Sternen4/5 (2)
- Exponential Word Problems 1Dokument1 SeiteExponential Word Problems 1Rosemarie MendozaNoch keine Bewertungen
- Sample - Lcat LumsDokument8 SeitenSample - Lcat LumsaumrrqNoch keine Bewertungen
- Ambulance Chasing Group 4Dokument15 SeitenAmbulance Chasing Group 4zahreenamolinaNoch keine Bewertungen
- Patient Autonomy and RightDokument24 SeitenPatient Autonomy and RightGusti Ngurah Andhika P67% (3)
- Leadership & Team EffectivenessDokument29 SeitenLeadership & Team Effectivenessshailendersingh74100% (1)
- Essay Writing FCE Part 1 - Sample Task # 5 - Technological DevelopmentsDokument3 SeitenEssay Writing FCE Part 1 - Sample Task # 5 - Technological DevelopmentsMaria Victoria Ferrer Quiroga100% (1)
- The Problem of EvilDokument13 SeitenThe Problem of Evilroyski100% (2)
- A Level Mathematics - Practice Paper - 7.4 - Differentiation in ContextDokument9 SeitenA Level Mathematics - Practice Paper - 7.4 - Differentiation in ContextZaka AhmedNoch keine Bewertungen
- Counting Methods: Permutations CombinationsDokument31 SeitenCounting Methods: Permutations CombinationsMark B. BarrogaNoch keine Bewertungen
- Validity & RealibilityDokument13 SeitenValidity & RealibilityaidilubaidillahNoch keine Bewertungen
- Waiting For GodotDokument9 SeitenWaiting For GodotKNoch keine Bewertungen
- 6 Upper and Lower BoundDokument20 Seiten6 Upper and Lower Boundmohamed aimanNoch keine Bewertungen
- An Interview With Thomas Metzinger What Is The SelfDokument2 SeitenAn Interview With Thomas Metzinger What Is The SelfIdelfonso Vidal100% (1)
- Limits and Continuity II Presentation SlidesDokument37 SeitenLimits and Continuity II Presentation SlidesS.m. ChandrashekarNoch keine Bewertungen
- Mathematics Course Companion SLDokument142 SeitenMathematics Course Companion SLAziz KarimNoch keine Bewertungen
- The Ultimate ECAA Guide: Economics Admissions Assessment. Latest specification with 300+ practice questions with fully worked solutions, time saving techniques, score boosting strategies, and formula sheets.Von EverandThe Ultimate ECAA Guide: Economics Admissions Assessment. Latest specification with 300+ practice questions with fully worked solutions, time saving techniques, score boosting strategies, and formula sheets.Noch keine Bewertungen
- Practice Makes Perfect in Geometry: Angles, Triangles and other Polygons with AnswersVon EverandPractice Makes Perfect in Geometry: Angles, Triangles and other Polygons with AnswersNoch keine Bewertungen
- Mathematics P1 - January 2019 (Mark Scheme)Dokument29 SeitenMathematics P1 - January 2019 (Mark Scheme)KatNoch keine Bewertungen
- 2 Philosophy (1) HTMDokument5 Seiten2 Philosophy (1) HTMBence BadarNoch keine Bewertungen
- 5.integral Calculus Objectives:: DX DyDokument16 Seiten5.integral Calculus Objectives:: DX DyAndyMavia100% (1)
- Roles and Competencies of School HeadsDokument3 SeitenRoles and Competencies of School HeadsPrincess Pauline Laiz91% (23)
- Tables of Laguerre Polynomials and Functions: Mathematical Tables Series, Vol. 39Von EverandTables of Laguerre Polynomials and Functions: Mathematical Tables Series, Vol. 39Noch keine Bewertungen
- A Level Mathematics Practice Paper 8Dokument12 SeitenA Level Mathematics Practice Paper 8api-351804653Noch keine Bewertungen
- Volumes of RevolutionDokument7 SeitenVolumes of RevolutionDegresFernandezPalomaNoch keine Bewertungen
- KS3 Maths CurriculumDokument16 SeitenKS3 Maths CurriculumMajid Bahmani100% (1)
- Argand Diagrams: Modulus, Argument and Polar FormDokument10 SeitenArgand Diagrams: Modulus, Argument and Polar FormZazliana Izatti100% (1)
- Math Studies Financial MathsDokument7 SeitenMath Studies Financial MathsGirish MishraNoch keine Bewertungen
- Winter HW 2015 Math HL G12Dokument9 SeitenWinter HW 2015 Math HL G12MishaZetov100% (1)
- Grade 10 Maths Book RATIOSDokument23 SeitenGrade 10 Maths Book RATIOSMartin HillNoch keine Bewertungen
- S2 Revision NotesDokument2 SeitenS2 Revision NotesimnulNoch keine Bewertungen
- The Function of Composition and InverseDokument20 SeitenThe Function of Composition and InversenormasulasaNoch keine Bewertungen
- WMA12 SampleDokument5 SeitenWMA12 Samplejyf97ybqxyNoch keine Bewertungen
- Derivatives of FungtionDokument15 SeitenDerivatives of FungtionnormasulasaNoch keine Bewertungen
- Schoolisfun's Math Level 2 Subject Test Guide and FormulasDokument40 SeitenSchoolisfun's Math Level 2 Subject Test Guide and Formulassudhakaralla1100% (2)
- Arithmetic Progression CBSE Class 10thDokument31 SeitenArithmetic Progression CBSE Class 10thVijay Kumar100% (1)
- Scotch 3cdmas Mock ExamDokument32 SeitenScotch 3cdmas Mock ExamFredNoch keine Bewertungen
- 2.2 Even Odd FunctionsDokument4 Seiten2.2 Even Odd FunctionsMuhammad AhmedNoch keine Bewertungen
- 9709 Mathematics: CambridgeDokument8 Seiten9709 Mathematics: CambridgeanzaaariNoch keine Bewertungen
- Math3B TrigIntegrals SolutionsDokument8 SeitenMath3B TrigIntegrals SolutionsZander Rein FernandezNoch keine Bewertungen
- Monday 24 May 2021: Further Pure MathematicsDokument6 SeitenMonday 24 May 2021: Further Pure MathematicsFarayan IslamNoch keine Bewertungen
- Complex NumbersDokument25 SeitenComplex NumbersAtib ShaikhNoch keine Bewertungen
- New A-Level Maths For Edexcel: Year 1 & 2 Exam Practice WorkbookDokument10 SeitenNew A-Level Maths For Edexcel: Year 1 & 2 Exam Practice WorkbookStudyHub DhakaNoch keine Bewertungen
- C BX Ax: Math 154B Name - Completing The Square WorksheetDokument2 SeitenC BX Ax: Math 154B Name - Completing The Square Worksheetapi-241187529Noch keine Bewertungen
- Mathematics Internal Assessment OoDokument7 SeitenMathematics Internal Assessment OoSigne Sofia PersdotterNoch keine Bewertungen
- Matrices and Basic Calculus For Non Majors-MT161Dokument11 SeitenMatrices and Basic Calculus For Non Majors-MT161Hamisi Mzari100% (1)
- Indices LogDokument25 SeitenIndices Logadeskitoku100% (1)
- BMOS MENTORING SCHEME (Intermediate Level) October 2011 (Sheet 1) Solutions and Explanatory NotesDokument4 SeitenBMOS MENTORING SCHEME (Intermediate Level) October 2011 (Sheet 1) Solutions and Explanatory NotesRaj Tomar RajsuryanNoch keine Bewertungen
- Mathematics 3CD Exam Calc Free 2011 PDFDokument12 SeitenMathematics 3CD Exam Calc Free 2011 PDFTejajjjNoch keine Bewertungen
- BINOMIAL SeriesDokument25 SeitenBINOMIAL SeriesBench AminNoch keine Bewertungen
- Arithmetic & Geometric Sequence Reminder - IB Mathematics Diploma ProgrammeDokument2 SeitenArithmetic & Geometric Sequence Reminder - IB Mathematics Diploma ProgrammeМаксим БекетовNoch keine Bewertungen
- Criterion B Lab ReportDokument9 SeitenCriterion B Lab ReportNigar-Banu KarimovaNoch keine Bewertungen
- Limits and ContinuityDokument25 SeitenLimits and Continuitypranav kale100% (1)
- Mathematics Specialist Stage 3C 3D Calc Free 2014Dokument20 SeitenMathematics Specialist Stage 3C 3D Calc Free 2014gragon.07Noch keine Bewertungen
- Parabolas - Intro Practice - ExtraDokument2 SeitenParabolas - Intro Practice - Extraapi-276566085Noch keine Bewertungen
- Inequalities Worksheet #01, Algebra Revision From GCSE Maths TutorDokument2 SeitenInequalities Worksheet #01, Algebra Revision From GCSE Maths Tutorgcsemathstutor100% (1)
- Quadratic EquationDokument1 SeiteQuadratic EquationEmyRaNoch keine Bewertungen
- Matrices and Calculus-2021 - SyllabusDokument2 SeitenMatrices and Calculus-2021 - Syllabusbalaji gopalNoch keine Bewertungen
- C1 Algebra - Surds and IndicesDokument30 SeitenC1 Algebra - Surds and IndicesYounger Boxer Metalic100% (1)
- Calculus and Analytical GeometryDokument8 SeitenCalculus and Analytical Geometrynep llNoch keine Bewertungen
- Service Tower Problem - Solutions: Adapted From Module 2: Worksheet 6 in Precalculus: Pathways To CalculusDokument5 SeitenService Tower Problem - Solutions: Adapted From Module 2: Worksheet 6 in Precalculus: Pathways To Calculusapi-287216602100% (1)
- A Level Mathematics - Practice Paper - 7.5 - Differential EquationsDokument6 SeitenA Level Mathematics - Practice Paper - 7.5 - Differential EquationsZaka AhmedNoch keine Bewertungen
- Revision Notes: Bob Francis 2005Dokument7 SeitenRevision Notes: Bob Francis 2005WillMeadNoch keine Bewertungen
- Practice PaperDokument206 SeitenPractice PaperTharshanth Bala100% (1)
- Examiner Tips For O Level Additional Mathematics 4037 FINALDokument6 SeitenExaminer Tips For O Level Additional Mathematics 4037 FINALAamirJavaid0% (1)
- Legacy of Ansel Adams and Minor WhiteDokument7 SeitenLegacy of Ansel Adams and Minor WhiteMaria DiamantopoulouNoch keine Bewertungen
- Phil KnightDokument14 SeitenPhil KnightJon Snow0% (1)
- Listening Skills: The Process of ListeningDokument5 SeitenListening Skills: The Process of ListeningRadhika VekariaNoch keine Bewertungen
- Yes, Economics Is A Science - NYTimes PDFDokument4 SeitenYes, Economics Is A Science - NYTimes PDFkabuskerimNoch keine Bewertungen
- 3rd and 4th Quarter TosDokument2 Seiten3rd and 4th Quarter TosMary Seal Cabrales-PejoNoch keine Bewertungen
- Chapter 1-Law and Legal ReasoningDokument9 SeitenChapter 1-Law and Legal Reasoningdimitra triantosNoch keine Bewertungen
- The Downfall of The Protagonist in Dr. FaustusDokument13 SeitenThe Downfall of The Protagonist in Dr. FaustusRaef Sobh AzabNoch keine Bewertungen
- Nieva Vs DeocampoDokument5 SeitenNieva Vs DeocampofemtotNoch keine Bewertungen
- Writing An Academic EssayDokument9 SeitenWriting An Academic EssayKerryNoch keine Bewertungen
- Faulkner Sound and FuryDokument3 SeitenFaulkner Sound and FuryRahul Kumar100% (1)
- David ch1 Revised1Dokument18 SeitenDavid ch1 Revised1Abdulmajeed Al-YousifNoch keine Bewertungen
- BeatitudesDokument2 SeitenBeatitudesvaanashe_basch7201Noch keine Bewertungen
- Lesson Plan The Mountain That Loved A BIRD by Sheena E. BernalDokument6 SeitenLesson Plan The Mountain That Loved A BIRD by Sheena E. BernalSheEna Brnl100% (1)
- Boscombe Valley MisteryDokument20 SeitenBoscombe Valley Misteryronie1988Noch keine Bewertungen
- Test 16 1-10-: Vocabulary / Test 16 (60 Adet Soru) Eskişehir YesdđlDokument5 SeitenTest 16 1-10-: Vocabulary / Test 16 (60 Adet Soru) Eskişehir Yesdđlonur samet özdemirNoch keine Bewertungen
- Linking Employee Satisfaction With ProductivityDokument6 SeitenLinking Employee Satisfaction With Productivityani ni musNoch keine Bewertungen
- Connotative Vs Denotative Lesson Plan PDFDokument5 SeitenConnotative Vs Denotative Lesson Plan PDFangiela goc-ongNoch keine Bewertungen
- Electrostatic 15: Part No. Topic & Lecture Name DurationsDokument2 SeitenElectrostatic 15: Part No. Topic & Lecture Name DurationsGourab RoyNoch keine Bewertungen
- Work Motivation & Job Design (Lec. 6, Chap. 7) - UPDATED2Dokument14 SeitenWork Motivation & Job Design (Lec. 6, Chap. 7) - UPDATED2AnnasNoch keine Bewertungen