Symbols and Units: Script Fonts Are Used For Physical Quantities and in Bold Font

Symbols
and Units
Symbols in italic or script fonts are used for physical quantities and in bold font
for vectors or matrices. Roman font symbols are used for labels and units e.g. A
is the Helmholtz free energy, but A is a label (e.g. of the left compartment in Fig.
1.1); W is the amount of work, but W is a unit of power [1 W = 1 J/s]. For the few
symbols that have multiple meanings (e.g., a), the most common one is listed
first. SI units for the corresponding physical quantities are given in brackets when
appropriate.
Symbols Latin alphabet
A
A
a
B
B
b
C
c
D
d
d
E
F
F
f
f
G
g
g
H
h
h
i, j
K
k
Helmholtz free energy [J (kg m2 )/s2]

area [m2]
activity [dimensionless] ; constant in property relationships [units vary]
second virial coefficient [m3 / mol]
extensive thermodynamic property (e.g. U, V, S, A, H or G) [units vary]
constant in property relationships [units vary]
heat capacity [J/(mol K)]; concentration [mol/m3] ;
third virial coefficient [mol2/ m6]
constant in property relationships [units vary]
diffusion coefficient [m2/ s]
diameter [m]
discriminant of quadratic polynomial
energy [J (kg m2) / s2]
force [N (kg m) / s2]
macroscopic degrees of freedom [integer]
fugacity [Pa 1 kg/(m s2)]
mathematical function
Gibbs free energy [J (kg m2) / s2]
acceleration of gravity [ = 9.81 m/s2 at sea level]
mathematical function
enthalpy [J (kg m2) / s2]
height [m]
mathematical variable or function
species indices [integers]
reaction equilibrium constant [units vary]
spring constant [kg / s2 = N/m]
ii
Symbols and Units
Symbols Latin alphabet (cont.)

k
number of streams [integer]
kB
Boltzmanns constant, R/NA [= 1.380651023 J/K]
kij
interaction parameter in equations of state
l
length or displacement [m]
M
molar mass [kg/mol]
M
matrix of stoichiometric coefficients
m
mass [kg]; chain length [integer]
N
number of moles [mol]
NA
Avogadros number [ = 6.02211023 mol1]
n
number of components [integer]
P
pressure [Pa kg/(m s2) = J/m3; also bar 105 Pa]
P
probability [dimensionless]
p
momentum [kg m/s]
Q
heat [J (kg m2) / s2]
Q
canonical partition function [dimensionless]
q
quality of mixed vapor/liquid stream (fraction vapor) [dimensionless]
q
molecular partition function [dimensionless]
R
Ideal-gas constant [ = 8.3145 J/(mol K)]
R
reactant species (vectors of elemental content)
r
intermolecular distance [nm]; number of independent reactions [integer]
S
entropy [J/K)]
T
temperature [K]
t
time [s]
U
internal energy [J (kg m2) / s2]
U
interaction energy between molecules
u
velocity [m/s]
V
volume [m3, also L 0.001 m3 = 1000 cm3]
W
work [J (kg m2) / s2]
w
mass fraction [dimensionless]
w
X
a chemical species
x
mole fraction [dimensionless] ; horizontal position [m]
x
y
mole fraction [dimensionless]
y
Z
compressibility factor ( PV / RT )
z
vertical position [m]
z

Symbols Greek alphabet

P
expansion ratio [dimensionless]

coefficient of thermal expansion [1/K]
Symbols and Units
iii
Symbols Greek alphabet (cont.)
inverse temperature, 1/kBT [J1]

activity coefficient; ratio of heat capacities CP/CV [dimensionless]

small difference (as prefix) ; solubility parameter [J1/2cm3/2]

difference (as prefix)

energy parameter in intermolecular potential functions [J]

coefficient of performance for cooling cycle [dimensionless, can be > 1]

efficiency of thermal engine [dimensionless, < 1]

thermometric temperature [ C]
T
isothermal compressibility [1/Pa]

multiplication factor [dimensionless]

chemical potential [J/mol]

stoichiometric coefficient of a species [dimensionless]

reaction extent [mol]

a Legendre transform of the fundamental equation [J/mol]

ratio of circumference to diameter of a circle [3.14159]

osmotic pressure [Pa kg/(m s2) = J/m3; also bar 105 Pa]

density [mol/m3 or kg/m3]

distance in intermolecular potentials [m; also 1010 m]

fugacity coefficient [dimensionless]

volume fraction [dimensionless]

number of phases in a system [integer]

Flory interaction parameter [dimensionless]

acentric factor [dimensionless]

number of microstates [dimensionless]

Modifiers
Intensive properties denoted by underscore (e.g. U_ is the energy per mole or kg)
Partial molar quantities denoted by overbar (e.g. Hi is the partial molar enthalpy of
component i)
Rate of change with time or flow rate is denoted by overdot (e.g. !N is the change of
the number of moles per unit time or the flow rate of a stream)

Subscripts and superscripts
constant-pressure property: subscript P
constant-volume property: subscript V
coexistence (phase equilibrium) property: superscript sat
critical-point property: subscript C
excess property: superscript EX
formation property: subscript form
ideal-gas property (omitted if the context is clear): superscript IG
ideal mixture: superscript IM

iv
Symbols and Units
infinite-dilution property: superscript

Subscripts and superscripts (cont.)
liquid phase property: subscript L
mixing property: subscript mix
non-dimensional property: superscript *
normal boiling point property: subscript b
property at the vapor pressure: superscript VP
reaction property: subscript rxn
reduced property: subscript r (e.g. Tr = T/TC)
reference or standard state: superscript 0
reversible process: superscript rev
vapor phase property: subscript V

Braces
{ }
indicates a set of independent mole numbers or mole fractions of compo-

nents in a mixture: { N } means the set of N1, N2, Nn , and { x } means the set
of x1, x2, xn1 .

Abbreviations
FE
QED
rxn
vdW

fundamental equation
quod erat demonstrandum (Latin for which was to be demonstrated)
reaction
van der Waals
Chapter 1. Introduction
1.1 What is Thermodynamics?
The term thermodynamics comes from the Greek words o+,
meaning heat dynamics (motion). Definitions of the term include:
The branch of physical science that deals with the relations between heat
and other forms of energy (such as mechanical, electrical or chemical ener-
gy) and, by extension, the relationships and interconvertibility of all forms
of energy. [New Oxford American Dictionary]
The branch of physical science concerned with equilibrium in material

systems and the changes that occur as a result of the interactions with oth-
er systems. [Encyclopdia Britannica Online]
The study of restrictions on the physical properties of matter that follow

from the symmetry properties of the fundamental laws of physics. [Callen]
The first two definitions contain terms that require their own definitions
(heat and equilibrium, respectively) while the third is extremely general but
also a bit less informative. It is clear from these definitions, however, that thermo-
dynamics is a general tool applicable to many types of physical systems. For exam-
ple, while we will not be dealing with systems of this type here, thermodynamic
principles can be used to analyze properties of black holes in astrophysics. The
power of thermodynamics is that it generates useful relationships that are both
rigorous and widely applicable, from a small number of postulates supported by
experimental observations. Strong justification for the postulates is provided by
using them to make concrete predictions, which are then verified by comparisons
against real-world data.
In this book, the focus is primarily on classical thermodynamics of fluids and
solids at conditions for which external magnetic, electrical and gravitational fields
have negligible influence on the properties of the systems of interest. Some refer-
ences will, however, be made to the microscopic basis of thermodynamic proper-
ties, even though one can obtain all the relations of classical thermodynamics

Material from Essential Thermodynamics, Drios Press (2011), A.Z. Panagiotopoulos

Hawking, S. W., Particle Creation by Black Holes, Commun. math. Phys., 43:199-220
(1975).
without making any assumptions about the microscopic constitution of matter.

The microscopic point of view is becoming increasingly important in modern en-
gineering, which seeks control of matter at near-atomistic (nm) length scales.
Understanding thermodynamics is of fundamental importance for many
branches of science and engineering. Our point of view in this book is that of chem-
ical engineers, who need to answer questions such as:
How much work is needed to compress a gas?
At a particular temperature and pressure, will a certain liquid vaporize?
What is the solubility of a pollutant in water and in the fat tissue of river
fish?
How far will a chemical reaction proceed in a vessel of known volume

loaded with given amounts of reactants? How can we maximize the yield
of desired products and minimize unwanted side reactions?
How can we modify a protein in order to maximize its thermal stability?
Under what conditions will a certain surfactant form micellar aggregates?
Are two polymers compatible (miscible) with each other?
What is the maximum amount of electricity that can be obtained from a ge-
othermal reservoir?
For many of the questions above, other considerations, such as inefficiencies in

mechanical devices, rates of diffusion, and kinetics of chemical reactions often play
a crucial role. However, thermodynamics provides the driving force for any trans-
formation of energy or material condition. It also places hard limits that cannot be
exceeded, irrespective of how clever the design of a specific process might be.
1.2 Thermometric and Ideal-Gas Temperature Scales

The need to quantify the intuitive notion of hot and cold (e.g. boiling water ver-
sus ice) led to the development of simple instruments, such as liquid-in-glass
thermometers that produce an objective measure the length of a liquid column
that correlates with the subjective feeling of warmth. The simple experimental
layout of Fig. 1.1 can be used to confirm that isolated systems tend to approach the
same thermometric temperature when contacted via a thin metal wall. This state-
ment is sometimes referred to as the Zeroth Law of thermodynamics. The two
systems A and B are considered to be in thermal equilibrium after a sufficiently
long time has passed and the thermometric temperatures have become equal, A =
B. It has been empirically determined that two systems in thermal equilibrium
can exist over long periods of time at quite different pressures and compositions, if
the boundary between them is rigid and impermeable to mass.
1.2 Thermometric and Ideal-Gas Temperature Scales

Figure 1.1 Experimental layout for measuring equality of thermometric tem-
peratures at equilibrium.
A thermometric temperature scale can be established by defining a standard

measurement device including its physical dimensions, working fluid (e.g. Hg),
materials of construction (type of glass), as well as at least two reference points.
For example, the two reference points in the commonly used Celsius temperature
scale are (i) the triple-point condition at which pure liquid water coexists with sol-
id ice and water vapor, 1 = 0.01 C and (ii) the boiling point of pure water at at-
mospheric pressure, 2 = 100 C. While it is not obvious a priori that these condi-
tions are reproducible and unique, many careful measurements have established
that they do establish a reliable empirical temperature scale.
A different temperature scale that turns out to play a key role in thermody-
namics is the one provided by the volumetric properties of low-pressure gases.
The key observation here is that the product of pressure and molar volume, P V , for
gases at sufficiently low pressures, is a linear function of thermometric tempera-
Figure 1.2 Volumetric properties of low-pressure gases.
ture, as shown schematically in Fig. 1.2:
PV = a + b
(1.1)
The linear relationship of Eq. 1.1 is only valid for a limited range of thermometric
temperatures and breaks down at low temperatures (hence the dashed line in the
figure). Setting the values for constants a and b effectively defines a thermometric
temperature scale; a particularly simple and appealing choice is b = 0, for which the
temperature scale becomes the thermodynamic temperature T. In this case, a is
identified as the ideal gas constant and has the value R = 8.3145 J/(mol K). Eq. 1.1
then becomes:
PV = RT
(1.2)
The relationship between thermodynamic and Celsius temperature scales is:

T [K] = [C] + 273.15
(1.3)
In many problems in this book we will perform calculations to 3 significant figures,

setting T [K] [C] + 273 .
1.3 Systems and Boundaries

A key concept in thermodynamics is the system, which is simply a well-defined re-
gion of space. This region of space does not need to be stationary it can be mov-
ing as a function of time. Once we have decided which region of space we are de-
fining as the system, the environment is defined as everything that is not part of the
system; the surface dividing the system from its environment is called the bounda-
ry. For example, in Fig. 1.1, one could choose as the system of interest compart-
ment A, compartment B, or both compartments taken as a whole. The best system
choice to facilitate thermodynamic analysis of a problem is often not obvious.
However, this choice cannot change the physical properties of the real system be-
ing analyzed, or the results of thermodynamic analysis of the system. For example,
the final temperatures and pressures after a certain physical process has proceed-
ed to equilibrium cannot depend on the (arbitrary) division of the universe into
system and environment.
Systems are characterized by the types of exchanges (flows) that take place
across their boundaries, as follows:
Open / Closed: If system boundaries allow the flow (exchange) of mass be-
tween system and environment, then the system is characterized as open; in
the opposite case we have a closed system. For example, the act of pulling the
ring at the top of a soda can converts it from a closed to an open system.
1.3 Systems and Boundaries
Movable / Rigid: If system boundaries are deformable, then the shape of the
system can change and its volume is not constant; in the opposite case the vol-
ume of the system is fixed.
Adiabatic / diathermal: Experiments on systems similar to the two-compart-
ment insulated container shown in Fig. 1.1 have demonstrated that different
materials and wall thicknesses result in substantially different rates of tem-
perature equalization on the two sides of the partition. An idealized limiting
case is that of a partition that does not allow any observable changes in tem-
perature of the compartments, as long as no other energy input is provided to
them. In this limiting case, the boundary is characterized as adiabatic (a tech-
nical term meaning not allowing passage). The conceptual opposite of an ad-
iabatic boundary is denoted as diathermal (e.g., a thin metal wall).
A system surrounded by rigid, impermeable and adiabatic boundaries is isolat-
ed.
This classification of boundaries seems somewhat arbitrary. How rigid does a
boundary have to be to qualify as such? Are the thin walls of a soda can sufficient-
ly rigid? Even the apparently simple question of whether a system is open or
closed cannot really be answered unless some characteristic time of interest is first
defined. To illustrate this point, consider the following example.
Example 1.1
A small, hermetically sealed glass capsule contains He gas at a pressure of P = 2 bar;
the environment is air at atmospheric pressure. The capsule glass walls have a
thickness of 0.1 cm. Is this system closed or open?

Clearly, the initial reaction would be to think of a sealed glass capsule as a
closed system. However, one may recall that helium seems to be able to escape
from apparently sealed environments, such as the interior of rubber party bal-
loons (which deflate after a few hours). Analysis of this problem requires the cal-
culation of a characteristic time for diffusion through the l = 0.1 cm glass walls. The
diffusion coefficient of He through glass is D = 8109 cm2/s at T = 300 K. Dimen-
sional analysis (which simply means combining D and l so that the result has units
of time) gives t = l 2/ D , so that:
l2
0.1 0.1!cm 2
t= =
= 1.2 10 6 !s! !14!d
9
2
D
8
10
!cm
/s
!
What can we conclude from this calculation? If the time scale of interest is much
less than 14 days, closed-system thermodynamic analysis is appropriate. Closed-
system analysis predicts that the final pressure inside the capsule remains at P =

Rogers, W. A. et al., "Diffusion Coefficient, Solubility, and Permeability for Helium in

Glass," J. Appl. Phys. 25:868-875 (1954).
2 bar; this is in agreement with observations at short times. However, if the time
scale of observation is much greater than 14 days, the system can be analyzed as
an open system with respect to the He gas. The final pressure depends on whether
sufficient time is allowed for diffusion through the glass walls of O2 and N2 from
the outside. The interior pressure is likely to drop to a very low value and then
eventually recover (after many years the diffusion of O2 and N2 is much slower
that that of He) to match the external pressure and composition.
In general, correct thermodynamic analysis will lead to agreement with exper-
imental observations if the assumptions made when performing the thermody-
namic analysis (closed / open system, diathermal / adiabatic, etc.) are consistent
with the real system and time scale of interest.
1.4 Equilibrium States

A basic postulate of thermodynamics is that stable equilibrium states exist for sys-
tems with well-defined external and internal constraints the domain of applica-
bility of classical thermodynamics is precisely these equilibrium states. Such states
are usually obtained after a sufficiently long time has passed so that the observa-
ble properties of systems no longer change with time; it should be emphasized
here that the condition of no change with time is necessary but not sufficient for
characterizing equilibrium states.
The concept of time scales illustrated in the previous section applies here as
well, as it is clear that in order to determine that a property does not change, one
needs to observe it over a certain time scale of interest. One may be tempted to
suggest that the correct thermodynamic equilibrium state of a system is the one
at extremely long times. However, this can lead us down paths that we may not
want to take as engineers try searching the web for Exasecond to obtain an in-
triguing list of transformations that are expected to occur over truly long time
scales. For example, elements lighter than iron are in principle metastable with
respect to nuclear fusion, but these transformations do not take place on any con-
ceivable time scale, except in the interior of stars. Closer to engineering applica-
tions, many chemical reactions proceed extremely slowly at room temperature,
e.g. that of gaseous O2 with H2 in the absence of a catalyst. A mixture of these two
gases can be analyzed as a non-reacting equilibrium thermodynamic system, as
long as no spark or catalyst is present.
Equilibrium
states are char-
acterized by
n+2 independ-
ent variables
For closed systems with no internal boundaries and containing known

amounts of n chemical species (components), equilibrium states are defined as
states that can be fully characterized by exactly 2 thermodynamic variables such
as the temperature, pressure, or overall volume. However, not all choices of varia-
bles are appropriate; for example, temperature and pressure are not independent
variables for a one-component system that contains two coexisting phases. It was
1.4 Equilibrium States
mentioned in the previous paragraph that some systems do not reach equilibrium
states even after a long time; a typical example is common silicate glass. In a non-
equilibrium system, additional information, such as the thermal history of the ma-
terial, is also necessary to characterize its state.

Chapter 2. Work, Heat, and Energy

The establishment of heat as a form of energy that can be partially converted into
useful work was a key impetus for the development of thermodynamics as a mod-
ern science in the nineteenth century by Sadi Carnot, James Joule and William
Thompson (Lord Kelvin). The generation of useful work continues to be a funda-
mental underpinning of our technological civilization. For example, we convert
between different forms of energy when powering trains, planes, automobiles, and
boats, when providing a comfortable environment with lighting, cooling, and air
conditioning, or when we perform physical and chemical transformations in
manufacturing. Electricity generation using coal, natural gas, or nuclear fission,
and locomotion using internal combustion engines also depend upon the trans-
formation of heat into other, more useful, forms of energy.
The main objective of the present chapter is to establish the fundamental rela-
tionships between work, heat, and the energy of closed and open systems. Energy
conservation is often called the First Law of thermodynamics. A First Law bal-
ance is usually the starting point for analysis of processes and systems of interest
to this book. Two important quantities, the energy and enthalpy are defined in this
chapter. In order to provide example applications of First Law balances to systems
of common interest in engineering practice, we also discuss energies and enthal-
pies of ideal gases, and how to obtain thermodynamic data for real fluids and solids.
2.1 Mechanical Work

A work interaction between two systems occurs when their boundary moves un-
der the action of a force F. For one-dimensional displacement over a differential
distance dx, the amount of work d/ W is:

/ = Fdx
dW
(2.1)
In Eq. 2.1, the amount of work is an inexact differential (denoted by a d with a slash
through it), meaning that the total amount of work between two specified posi-
tions generally depends on the path, since the force itself depends on the path. The
total amount of work produced for a finite displacement is:

2.1 Mechanical Work
(2.2)
W = F dx
!
On the schematic diagram of Fig.
2.1, the force is higher when the system
moves to the right relative to when it
moves to the left. This type of behavior
is called hysteresis and occurs in sys-
tems that have dissipation or friction.
Even when well lubricated, real me-
chanical systems are never completely
free of friction; internal gradients of

pressure or temperature also result in
Figure
2
.1

F
orce
v
ersus
d
isplacement
f
or
a
hysteretic behavior.

In 1845, James Joule performed ex-

periments measuring the changes in the
thermometric temperature of an insu-
lated tank of known contents, resulting
solely from mechanical work input. In
particular, a weight was made to de-
scend slowly (Fig. 2.2), producing work
in the form of motion of a stirrer. The
stirring action was shown to increase
the temperature of the working fluid by
an amount directly proportional (for
small temperature changes) to the
amount of work input. This established
that mechanical work could be con-
verted into heat. Through more pre-
cise measurements, the conversion fac-
tor was later established as 4.18 J/g/C
of temperature rise for water at ambi-
ent conditions.
system with hysteresis.

Figure 2.2 Schematic illustration of
Joules experimental setup for conversion
of mechanical energy into heat.

The reverse experiment, using a fluid to produce mechanical work, can also be
devised. Such work production is accompanied by a lowering of the fluids temper-
ature. Consider a piston of mass m confining a pure gas of temperature T0 and
pressure P0 in an insulated cylinder, with vacuum on the other side of the piston
(Fig. 2.3). Let us assume also that mg < P0A, where A is the cross-sectional area,
so that the weight of the piston does not balance the pressure from the gas. A stop
blocks the piston from moving. If the stop is suddenly removed, the gas will ex-
pand; if there is enough gas, the piston will reach the top of the tank, as shown in
Fig. 2.3, right side. What is the work interaction between the piston and the gas?
Clearly, work is done on the piston by the gas. The net amount of work needed to
lift the piston can be found from Eq. 2.2,
10

Figure 2.3 Piston and cylinder in insulated tank.
W
= F dz = mgh

! on!piston
(2.3)
where z is the vertical position. One can also obtain the amount of work performed
on the gas as it expands:

W
= PA dz = P dV
! on!gas
(2.4)
The negative sign is present here because we use the convention that work is posi-
tive if it is added to a system and negative if it is produced by a system. The pres-
sure of the gas becomes lower as it moves up, so that the integral of Eq. 2.4 re-
quires some effort to evaluate. Because of imbalance between the force of gravity
pulling the piston down and the force exerted by the gas, the piston will initially
accelerate upwards. However the container wall eventually stops the piston and
the final equilibrium state is reached with the gas at some Tf and Pf .

The system can be taken from the initial state (T0 , P0) to the same final state
(Tf , Pf) in a different way. Instead of letting the piston accelerate upwards to hit the
top wall and come to an abrupt stop there, a process can be devised to gradually
move it up by lifting a pile of sand. At the initial state shown in Fig. 2.4, the weight
of the sand and piston just about balance the pressure of the gas. By gradually re-
Figure 2.4 Piston-cylinder system with gradual lifting.
2.1 Mechanical Work
11
moving a few grains at a time, the piston can be lifted to the top of the container. In
order to ensure that the final state is the same as before, a large constant-volume
reservoir at Tf , the final temperature of the experiment in Fig. 2.3, is placed in con-
tact with the gas when the piston has reached the top. Since thermodynamic sys-
tems of one chemical component are fully defined by n+2 = 3 variables at equilib-
rium, specifying the amount of gas, its final volume and final temperature also sets
the final pressure to the same value as previously. However, by the time the piston
has reached the top of the cylinder, more work has been performed by the gas in
this case relative to that of Fig. 2.3. In addition to lifting the piston, the gas has lift-
ed some sand, as shown in Fig. 2.4. Where did the extra work for lifting the sand
come from? It must have come from heat interactions with the reservoir.
This and many other similar experiments establish that a form of energy is
transferred when temperature differentials exist between parts of a composite
system. When this form of energy is transferred into a substance, its temperature
increases. We now know that this energy is stored as kinetic and potential energy
of molecules, but at the time of Joules experiments the molecular hypothesis for
the composition of matter was not yet accepted. However, for classical thermody-
namics, the precise nature of this energy is immaterial: what is important is that it
can be obtained from macroscopic mechanical energy in a precisely quantifiable
fashion.
2.2 First Law for Closed Systems

A key fundamental postulate of thermodynamics is that there is an energy func-
tion E that depends solely on the state of a system. The change in energy, E, be-
tween two equilibrium states of a system such as the one described in the previous
section can be measured directly in experiments involving only mechanical work
interactions. Innumerable attempts by ingenious inventors to construct perpetual
motion machines that could generate energy without any permanent physical or
chemical transformations of their contents have failed. No such devices exist, for
reasons that are strongly entwined with the basic conservation principles of the
physical laws.
Experiments similar to those described in the previous section suggest that
when two systems are in intimate contact, energy that is not associated with mac-
roscopic mechanical forces can flow through their boundary. This hidden energy
needed to balance the books is defined as heat and denoted by the symbol Q. The
amount of heat exchanged between two systems can be measured by first estab-
lishing the energy function of either system using well-insulated (adiabatic) exper-
iments. In its simplest form, written for a closed system that cannot exchange mass
with its environment, the First Law of thermodynamics is written as:
First Law,
closed systems,
integral form
12
!E = Q +W
work and
heat sign
convention
(2.5)
This equation states simply that the change of en-

ergy of a system is due to addition of heat and mac-
roscopic (mechanical) work input. Both work and
heat are considered positive if performed on the
system of interest.
The energy E that appears on the left-hand side
of Eq. 2.5 can have a number of different manifesta-
tions, in particular as potential, kinetic, and internal
energy.

Figure 2.5 Mass in a gravita-
tional field.
Potential energy is due to the position of a system in a force field for example,
mass in a gravitational field or charge in an electrostatic potential. For a mass m in
a gravitational field (Fig. 2.5), the force is:

(2.6)

!F = mg
The work performed by the gravitational field when the mass moves from height
z1 to z2 is:

W = 2 mgdz = mg(z1 z2 )
z1
!
(2.7)
If z2 < z1 , work is positive, as it is performed on the system of interest by the ex-

ternal field.
Kinetic energy is the energy associated with macroscopic motion of parts of a
system. The kinetic energy change when a mass m is accelerated from rest (zero
velocity) to a final velocity uf can be found from:

d2x
du
dx
Ekin = Fdx !!!,!!!!where!!F = m 2 = m !!!!!!and!!!!u =
dx = udt
dt
dt
dt
!
u
f
du
1
!!Ekin = m udt = mudu = muf2
dt
2
0
!
(2.8)
The internal energy, denoted by the symbol U, is due to microscopic interac-

tions (intermolecular potential energy) and molecular motions (microscopic kinet-
ic, vibrational, rotational energy). U is an extensive thermodynamic function pro-
portional to the size of a system, U=NU. The molar (specific) energy U for equilib-
rium states of pure components is a function of two independent thermodynamic
variables (such as the temperature and volume). It can be measured through pure-
ly macroscopic observations, by performing an adiabatic change of the condition of
a system and observing the mechanical work input associated with the change. For
13
simplicity, we often omit the internal

adjective and refer to U simply as the
energy of a thermodynamic system.
The energy U is a key thermo-
dynamic quantity and will be central
in later derivations. When written as a
function of the other extensive varia-
bles of a system it becomes a funda-
mental equation for the thermody-

namic state of a system, as discussed
in detail in Chapter 5 of this book. We
Figure 2.6 Extension of a linear spring.
can write a differential form of the
First Law by considering changes to
the internal energy of a system resulting from the addition of small amounts of
work and heat:

/ + dW
/
!dU = dQ
(2.9)
In writing Eq. 2.9, we have assumed that there are no changes in kinetic or poten-
tial energy of the system. Even though the energy is a function of thermodynamic
state (hence it has a proper differential dU), both heat and work terms depend on
the path taken and are thus represented by inexact differentials.
In some cases, the distinction between internal and potential energy can be
somewhat arbitrary. For example, a simple linear spring (Fig. 2.6), exerts a force
on its environment that, for small extensions, follows the equation F = k(x x0),
where x is the instantaneous position of the end of the spring and x0 is the length at
rest. The energy change, E, of the spring is equal to the work input into the sys-
tem when the spring end moves from position x0 to x1:
x
x
k
(2.10)
E = W = 1 F dx = 1 k(x x0 )dx E = (x1 x0 )2
x0
x0
2

!
!
This change in energy can be considered to be the change in potential or internal
energy of the spring, depending on whether we adopt a macroscopic (mechanical)
or molecular point of view.
Example 2.1 A stretched rubber band

A rubber band follows the force-extension relationship of a linear spring. Consider
a stretched rubber band of length x = 0.20 m, with equilibrium (unstretched) length
x0 = 0.10 m and k = 500 N/m (coordinates are as in Fig. 2.6). The rubber band is at
room temperature. Now we allow the band to perform work by returning it to the
unstretched state, x = x0. The release takes place quickly enough so that no appre-
ciable heat transfer to the environment occurs during the release. The heat capaci-
First Law,
closed systems,
differential
form
14
ty, C = (U / T)l of the rubber band is 5 J/K, approximately independent of length.

Estimate the temperature change of the rubber band upon release.

The amount of work performed on the rubber band is given by Eq. 2.10,
W =
x0
F dx =
x0
k
k(x x0 )dx = (x x0 )2
2
500
N
W =
(0.2 0.1)2 ! m2 = 2.5!J
2
m
!
The work is negative because the rubber band has produced work on the envi-
ronment when the end-point was moved. From a First Law balance,
U = Q +W U = CT = W T =
W 2.5!J
=
C 5!J/K
T = 0.5!K

!
!
The quickest way to detect a temperature change for a rubber band being released
from a stretched state is to use your lips feel free to try this experiment at home,
using appropriate eye protection.

The potential energy of the rubber band was considered part of its internal ener-
gy U in this example. This is because the elastic response is due to molecular-level
changes within the rubber band.
Example 2.2 Work and Heat of Vaporization
Calculate the work and heat requirements for the process of vaporization of 1 mol
of liquid water from a closed container at two temperatures, T = 298 K and 373 K.
Vaporization for pure components takes place at constant pressure, called the va-
por pressure in vaporization, heat input is not accompanied by a temperature
increase, only a change of physical state. Properties of water and other substances
can be obtained from the NIST Chemistry WebBook, as explained in Appendix I.
The environment is at atmospheric pressure, Patm = 101 kPa.

Transformation of liquid into vapor is accompanied by a large volume change, so
the closed container needs to have flexible walls or be equipped with a movable
piston to allow for expansion, as shown in Fig. 2.7. The vapor pressure, liquid and
vapor energies, and volumes at 298 K are obtained from the NIST WebBook as:
P VP = 3.1417!kPa!
U L = 1.8772!kJ/mol;!!!U V = 43.397!kJ/mol
V = 0.0181!l/mol;!!V V = 787.36!l/mol
! L
An issue to be considered in this problem is the work to push back the atmos-
phere. Clearly, the piston experiences a different pressure on the left, !P VP , than on
15
the right, Patm ; a net force to the right is re-

!
quired to keep the piston in place; it is equal
to:
F = (Patm P VP )A ,
!
where A is the area of the piston. The force
is constant as the liquid vaporizes because
the pressures on the two sides of the piston
do not change. The net work required to
move the piston from the initial to the final
volume is
Wtotal = Fx = (Patm P VP )A x =
(Patm P VP )V =
= (101 3.14)103 Pa
!!!!(787.36 0.0181)10 m /mol!

W
= !77.05!kJ/mol
! total

Figure 2.7 Vaporization in a closed
container (volumes a re not drawn to
scale).

However, this work is not equal to the work
performed on the system most of it is performed on the atmosphere. The work
performed on the system is
Wsys = P VPA x = P VP V = 2.47!kJ/mol

!
W is negative because expansion of the system means it performs work on its

! sys
environment.
First Law balance for the closed system now gives:
U = Q +Wsys Q = U Wsys = U V U L Wsys = (41.52+ 2.47)!kJ/mol = 43.99!kJ/mol

!

At the normal boiling point (T = 373 K), the total work required Wtotal = 0, as the
pressures on the two sides of the piston are equal. The heat required is:
Q = U +Wsys = U + P VP V =
= (45.14 7.54)!+101(30.27 0.02)103 kJ/mol =
!= (37.60+ 3.05)!kJ/mol = 40.65!kJ/mol

The large change in internal energy on vaporization of a liquid is due to the need to
disrupt the attractive interactions acting between its molecules, which include hy-
16
drogen bonds in the case of water. As seen in this example, the internal energy
change is an order of magnitude greater than the P VPV term.
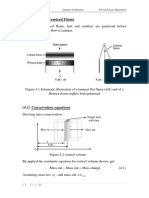
2.3 First Law for Open Systems

Many systems of interest have bound-
aries that are open to the flow of mass.
For example, modern chemical plants
typically operate using continuous-flow
process units, each with one or more
input and output streams. For open sys-
tems, we clearly need to consider the
energy carried by the streams entering

and leaving the control volume when
performing an energy balance. Consider
Figure 2.8 Open system.
an open system, into and out of which
with i = 1 ,2,,k, as shown schematically in Fig.
streams flow at (mass) rates m
! i
2.8. Only three streams are shown in the figure for simplicity. The system is de-
fined as the contents of the box outlined by the heavy black line and dashed lines
at the entrance points it does not include the material in the pipes leading into
and out of the container. The instantaneous mass of the system itself (which could
be changing with time) is m. For simplicity, we will assume that the whole system
has a single velocity u and vertical position z. The analysis can be easily general-
ized for systems with parts that have different velocities and vertical positions.
Conservation of energy can be generally written as
u2
!!!!!!!Rate!of!energy
d
U + m + gz =

dt
2
net!input!to!the!system
(2.11)
ui2
Emass!flow = m i U i + + gzi
2
i=1
!
(2.12)
!

The energy net input to the system contains heat and work terms, as well as flow
terms. Work and heat flows are represented by arrows in Fig. 2.8. The rate of work
input into the system is denoted by W ; this work input could be in the form of elec-
trical energy, or mechanical work through the action of pumps, compressors, or
pistons. The rate of heat input into the system is denoted by Q . The rate of energy
input due to the streams flowing in and out of the system, assuming that the quan-
tities m i are algebraic mass flow rates (positive for input streams and negative for
output), is:

Ui is the specific energy (on a mass basis) of stream i. However, there is one addi-
tional energy input that is not as obvious. It has to do with the work required to
17
push the input streams into the system

and the work produced by the output
streams as they come out. The easiest
way to understand this PV term is to
consider a simple system with one in-
put and one output stream (Fig. 2.9)
and a small interval of time during
which mass min enters the system and
mass mout leaves the system. Their

pressures are, respectively, Pin and Pout.

Now consider the closed system that Figure 2.9 PV work in an open system with
a single input and output stream.
consists of the original open system,

augmented by Vin = Vinmin and exclu-
ding Vout = Voutmout. The boundaries of this new system are shown by dotted lines
in Fig. 2.9. The volumes occupied by the masses min and mout may be very differ-

ent, if there are changes in the physical state of the material going through the sys-
tem (e.g. liquid going to vapor, gas being compressed or expanded). Now it should
be clear that the work term associated with the process of pushing min into the
system and getting mout out of the system is:

E
= Pin Vin PoutVout = Pin V!in min Pout V!out mout
! PV !work
in Pout V!out m
out
E
= PinV!in m
! PV !work

(2.13)
Combining Eqs. 2.11 through 2.13,
u2
U
+
m
+ gz = Q + W + Emass!flow + E PV !work
dt
2

u2
i U i + Pi V i + i + gzi
= Q + W + m
2
i=1
(2.14)
!
The combination U + PV is defined as a new thermodynamic function called the
enthalpy H. In Chapter 5, we will show that the enthalpy is also a fundamental
equation with the same information content as the energy U. At the moment,
however, we consider this as just a convenient way to write the energy balance
equation for an open system. The final result is:
u2
ui2
d
i H i + + gzi
U + m + gz = Q + W + m
dt
2
2

i=1
(2.15)
18
Often, the kinetic and potential energy terms are small; if these terms can be
ignored, the open-system energy balance becomes (now written on a molar basis):
First Law,
dU
open systems,
= Q + W + H in N in H out N out
(2.16)
dt
diff. form,
entering
leaving

streams
streams
!
no kinetic or
potential en-
In Eq. 2.16, we have split the sum over all input and output streams into two
ergy changes
terms, the first a summation over entering streams, N in , and the second over leav-
!
ing streams, N out , with all flows taken as positive. Another useful way to write Eq.
!
2.16 is by multiplying all terms by dt to obtain:
/ + dW
/ +
dU = dQ
entering!
streams
H in dN in
leaving!
streams
H out dN out
(2.17)
!
For steady-state operation, the left-hand side of Eqs. 2.16 or 2.17 (the change
of energy for the contents of the open system of interest) is zero. A further simpli-
fication can be obtained for the very special case of an open system at steady state,
which has only a single stream of flow rate N entering and leaving. For this highly
restrictive case, the First Law balance takes a particularly simple form, which may
be familiar to you from Materials and Energy Balances or other introductory
courses:

Q + W
N H out H in = NH
= Q + W H =

(2.18)
N
!
If the properties of entering and leaving streams do not vary over the time pe-
riod of interest, Eq. 2.16 can be integrated to give the analog of Eq. 2.5:
First Law,
open systems,
integral form,
no kinetic or
potential en-
ergy changes
U = Q +W +

entering
streams
Nin H in
leaving
streams
Nout H out
(2.19)
As previously, for a steady-state process, the change in the contents of an open sys-
tem is zero, so the left-hand side of Eq. 2.19 vanishes.
It is important here to discuss the various forms of the open-system First Law
balance that have just been presented. For example, Eqs. 2.18 and 2.19 may at first
appear to be quite confusing, given that 2.18 has a change of enthalpy on the left-
hand side, while 2.19 has a change of energy. However, the change of enthalpy in
Eq. 2.18 is of the material flowing through the open system, while the change of
energy of Eq. 2.19 is of the open system itself. Eq. 2.18 relies on several assump-
tions (steady state, single input-output), while 2.19 is more general, assuming only
constant properties of the entering and leaving streams over the period of interest.
Of course, the most general form of the First Law balance for open systems is Eq.
19
2.15, which does not require any assumptions this also makes it the most diffi-
cult expression to use in practice.
Example 2.3 Vaporization in an open system

Repeat the calculations of Example 2.2, now considering a steady-state flow pro-
cess producing 1 mol/s of steam from liquid water at its vapor pressure.

Let us consider a flow process (Fig.
2.10) with input and output streams at
the conditions of Example 2.2. Since
input and output streams are at the
same pressure, no pumping is required
to operate this process and the work
input is zero. A steady-state differ-
ential First Law balance gives:
dU
V
= Q + W + NH L NH
dt
Q = N H V H L
!

Figure 2.10 Vaporization in an open system.

We obtain values for the enthalpy

at saturation of water at 298 and 373 K and sub-

stitute in the expression above:
mol
kJ
kJ
45.87 1.88
= 43.99 !!at!298!K!!
s
mol
s
mol
kJ
kJ
Q =1
48.20 7.54
= 40.66 !!at!373!K
s
mol
s
!
Q =1
The amounts of heat required for the open-system process are equal (within nu-
merical precision) to the corresponding quantities for the closed-system process
of Example 2.2; there is no real difference between the two processes other than
accounting for the P VPV term. When considering a closed-system process, this
term appears as work explicitly produced by the expanding system. In an open
system, this work is contained in the enthalpy of the flowing exit stream.
Example 2.4 Thermodynamic Analysis of the Human Heart

A simplified schematic diagram of the human heart is shown in Fig. 2.11. Blood
from the body enters the heart in point A, at pressure PA = 0.66 kPa above atmos-
pheric. The pressure difference from the ambient pressure is defined as gauge

Inspired by problem 13.10 in Levenspiel, O., Understanding Engineering Thermo, Prentice-
Hall (1996).
20
pressure. Blood exits the right ventricle in point B on its way to the lungs, at gauge
pressure PB = 2.9 kPa. Oxygenated blood returns from the lungs in point C at gauge
pressure PC = 1.0 kPa and is in turn returned to the circulatory system through ar-
tery D at gauge pressure PD = 13 kPa. The normal blood flow rate (at rest) is
3
!V = 90!cm /s . The diameters of the veins and arteries are dA = 3.0 cm, dB = 2.5 cm,
dC = 2.8 cm and dD = 2.0 cm. Calculate the minimum power required for operation
of the heart, assuming no heat effects (!Q = 0 ) and a constant density of blood, = 1
g/cm3.

Since it is not clear that we can neglect kinetic
energy terms, we start with a full First Law bal-
ance (Eq. 2.15). At steady state, the time differ-
ential on the left-hand side of Eq. 2.15 is zero.
We also do not have significant potential energy
changes, as the arteries and veins all enter the
heart at roughly the same height, so gravitation-
al energy changes can be neglected.
4
u2
0 = Q + W + m i U i + Pi V i + i + gzi
2
i=1
(i)

Figure 2.11 Schematic diagram of
circulation in the human heart.
We are not given any information on the specific

energies Ui, but since blood going through the
heart does not change when flowing in the atria and out the ventricles, we must
have
4
m
iUi = 0

!i=1
We can obtain the velocities from the relationship:
2
D
V = uA = u
4
!
u=
4V
2
; uA =
490!cm3 /s!
2
3.14! !3.0 cm
= 12.7
cm
m
= 0.127
s
s
m
m
m
Similarly, we get uB = 0.183! , uC = 0.146! and uD = 0.286! .
s !
s
s
!
!
= V = V /V , we obtain:
Now substituting in Eq. (i), and using !m
4
u2
u2 u2 + u2 u2
i Pi V i + i = V PA PB + PC PD m
A B C D
W = m
2
2
i=1
21
cm3
m3
W = 90
106
0.66 2.9+1.013 103 Pa
s
cm3
2
2
2
2
kg 0.127 0.183 + 0.146 0.286 m2
J
0.09
W = (+1.282+ 0.004) = 1.286!W
2
s
2
s
s
!

Most of the work is needed for increasing the pressure (PV term); the change in
kinetic energy of the blood is negligible. The overall efficiency of mammalian
hearts is about 15%, so the actual power requirement is around 9 W this is the
chemical energy that needs to be provided in the form of ATP to the muscle tissue
driving the heart. The energy requirement per day is 9 W86400 s/d 800 kJ/d
190 kcal/d.
2.4 Ideal Gases

When performing quantitative energy balance calculations, it is necessary to have
information on how the pressure and temperature of the system of interest influ-
ence properties such as the density = N/V and internal energy U. Detailed discus-
sion of such equations of state can be found in Chapter 7. Here, we derive some
basic relationships for a special class of substances, ideal gases. In ideal gases, in-
teractions between molecules can be neglected. Real gases at low pressures ap-
proach this condition as the average distance between molecules becomes much
greater than the range of intermolecular forces. Using statistical mechanical meth-
ods introduced in Chapter 5, it can be shown that the pressure P of a system of N
non-interacting particles in a volume V is given by the relationship (see Example
5.8, p. 102, for a derivation):
(2.20)

!PV = NRT
R is called the ideal-gas constant and has the value R = 8.3145 J/(mol K). Since ide-
al gases consist of isolated molecules that do not feel the presence of each other,
their internal energy is simply the sum of energies of the individual molecules and
does not depend on density or pressure:
IG
IG

!U = NU (T )
(2.21)
IG
Here, we have written !U (T ) to emphasize that the molar energy in the ideal gas
state is a function of temperature.
The internal energy of ideal gases contains contributions from kinetic energy
of translation of the molecules in space, as well as rotational and vibrational mo-
tions. It is a function of temperature because molecules travel faster and rotational
and vibrational motions store more energy at higher temperatures.
22
Now let us consider heating an ideal gas in a container with rigid walls (so that
no work is performed, d/W = 0 ). Assuming that we can neglect the walls heat capac-
ity, we can write from a differential First Law balance on this closed system:
/ = NCVIGdT
dU IG = dQ
!
We have defined a new quantity, the heat capacity at constant volume:
(2.22)
IG
dU

(2.23)
C
dT

!
The heat capacity of ideal gases can be measured experimentally quite accu-
rately for relatively simple systems it can also be predicted theoretically to a high
level of accuracy. For example, for simple monoatomic gases (e.g. He or Ar) the
heat capacity at constant volume is
IG
V
C IG = 3R /2!!(monoatomic!gases)
! V
(2.24)
In general, each fully excited degree of freedom for a molecule contributes

R/2 to the constant-volume heat capacity for monoatomic gases the degrees of
freedom are translational motion in each of the three directions of space. Rotations
and vibrations provide additional degrees of freedom for more complex, polyatom-
ic molecules. While for monoatomic gases the ideal-gas heat capacity is independ-
ent of temperature, for more complex molecules the various degrees of freedom
become excited gradually as temperature rises and the ideal-gas heat capacity is a
function of temperature (see 7.2, pp. 139-141).
As density is increased, real systems deviate from the limiting ideal gas behav-
ior as the molecules feel the presence of each other and their intermolecular in-
teractions start contributing to the total energy. The internal energy per mole, U,
becomes a function of the density in addition to the temperature. In this general
case, we define the heat capacity as the partial derivative of the molar energy with
respect to temperature at constant volume:
U
CV
(2.25)
T V

!
Constant volume properties are sometimes called isochoric. Heat capacities of real
systems can be measured directly and can also be determined indirectly from the
ideal-gas values and the volumetric properties.
Now let us consider the case of heating an ideal gas, but at constant pressure
rather than constant volume. A differential First Law balance on a container fitted
with a piston to maintain constant pressure gives:

/ + dW
/ = dQ
/ PdV
!dU = dQ
23
2.4 Ideal Gases
We have used Eq. 2.2 to obtain d/W, with the force F = PA, so that Fdx = PdV. Since
pressure is constant, we can rearrange this expression to obtain:

!U = Q PV Q = (U + PV ) = H [constant-P]
(2.26)
In strict analogy to Eq. 2.23, we can define the constant-pressure (isobaric)

heat capacity for an ideal gas as:
IG
C PIG
dH
d IG
d IG
=
U + PV =
U + RT = CVIG + R
dT
dT
dT
(2.27)
!
As seen in Eq. 2.27, for ideal gases, the relationship between the heat capacities
at constant pressure and constant volume is particularly simple. The heat capacity
at constant pressure for ideal gases is a function of temperature only (not density
or pressure), just as was the case for the heat capacity at constant volume, C IG
V . In
the general case, for systems that cannot be described as ideal gases, the heat ca-
pacity at constant pressure is again defined as the temperature derivative of en-
thalpy:
H
1 H

(2.28)
CP =
=
N T N ,P T P

!
In general, the heat capacity at constant pressure is greater than the heat ca-
pacity at constant volume, but the relationship between the two is a non-trivial
function of the volumetric properties of the system.

Adiabatic expansion of ideal gases follows simple expressions that are useful
for analysis of many physical systems. The derivations below are valid only for
ideal gases. The differential change of energy, assuming uniform pressure P during
the expansion and no change in kinetic or potential energy is:
/ + dW
/ = PdV
dU = dQ
!

The change in energy can also be obtained from Eq. 2.22 (with N constant):

RT
dU = PdV NCVIGdT = NPdV = NPd
!
RT
CVIGdT = PdV = RdT +
dP
P
!

(2.29)
The relationships of Eq. 2.29 can be integrated in three different ways, depending
on the selection of independent variables. In particular, eliminating pressure from
the first equation and integrating from initial conditions (labeled 0) to a final state
(unlabeled) we obtain:
24
RT
dT
dV
CVIGdT = PdV CVIGdT =
dV CVIG
= R
V
T
V
!
V
T V CVIG V
=
= =

(2.30)
T0 V 0
V0
V0
!
In writing the last equality in Eq. 2.30, we have taken into account the fact that the
number of moles N is constant in this process, so that ratios of specific and total
volumes are the same. We have also defined the ratio of the heat capacities as
= C P /CV . Eliminating volume from Eq. 2.29 and integrating we obtain:
!

RT
dT
dP
dT
dP
CVIGdT = RdT +
dP (CVIG + R)
=R
C PIG
=R

P
T
P
T
P
!
R
IG
T P CP P
= =
T0 P0
P0
!
(2.31)
Finally, eliminating temperature from Eq. 2.29 and integrating we obtain:
PdV = C dT =
IG
V
CVIG
VdP =
! R

CVIG
R
IG
CV + R
R
P V
=
P0 V 0
d(PV ) =
CVIG
R
(PdV +VdP)
dP
dV
PdV C
= C PIG
P
V
IG
V
V
=
V0
PV = const.
(2.32)
Once again, N is constant in this process, so that ratios of specific and total volumes
are the same. The amount of work performed on an ideal gas during adiabatic
compression can be obtained from an integral First Law balance, if the heat capaci-
ty is independent of temperature:

U = Q +W W = NCVIG T
!
(2.33)
Example 2.5 Filling of a gas cylinder

An insulated rigid vessel of volume V initially contains Ni moles of an ideal gas at
temperature Ti. A pipe is now connected to the vessel and the same gas at temper-
ature Tin is pumped in, until the number of moles in the vessel becomes Nf. Obtain
an explicit expression for the final temperature in the vessel, Tf, in the form Tf = f (Ti
, Tin , Nf / Ni , CP). CP is the molar heat capacity of the gas at constant pressure, as-
25
2.4 Ideal Gases
sumed to be independent of temperature. There is no heat transfer between the

gas in the tank and the vessel walls during the transfer.

We start with a First Law balance on the contents
of the vessel at a time when there are N moles of
gas in it at temperature T, taking into account that
both heat and work terms are zero:
dU = H in dNin d(UN) = H in dNin

!

Figure 2.12. Vessel being filled
UdN + NdU = H in dNin = Hin dN

!
(i)
Note that dU and N refer to the vessel and are changing as it is being filled, while
Hin and dNin refer to the incoming stream, which has constant properties. For this

particular example, dN = dNin because there is only one input stream and any

change in the contents of the vessel comes from that stream; this is not generally
the case. Since the heat capacity CP is independent of temperature (and thus also is
CV = CP R), we can express the enthalpy and energy at any temperature T in terms
of reference values H0 and U0 at temperature T0:
T
U(T )U 0 (T0 ) = CV dT U(T ) = U 0 (T0 )+ CV (T T0 )

T0
H(T ) H 0 (T0 ) = C P dT H(T ) = H 0 (T0 )+ C P (T T0 )!,!with!!H 0 (T0 ) = U 0 (T0 )+ RT0

T0
!
A convenient choice for First Law balances involving ideal gases is to set T0 = 0 and

U0 = 0, which results in U(T) = CVT and H(T) = CPT. Even though such a choice is nev-
er made in thermodynamic tables of real fluids because the absolute zero in tem-
perature cannot be reached, any observable quantities (such as the temperature of
the vessel in this example) are independent of this choice of reference states.
Substituting U and H into expression (i) above and using = CP/CV , we obtain:
CV TdN + NCV dT = C PTin dN NCV dT = C PTin CV T dN

!
Nf
T
N
T T
dN
dT
= f
ln f = ln in f
Ti T T
N
Ni
Tin Ti
in
N
Tf = Tin i (Tin Ti )
Nf
!

2.5 Properties of Real Fluids

In general, gases deviate from ideal-gas behavior at most conditions of practical
interest. Liquids and solids are, of course, far from being ideal gases at all condi-
26
tions; their thermodynamic properties cannot be obtained at all from application

of the relationships of the previous section. Directly measurable thermodynamic
properties of real systems, such as the pressure at a given density and tempera-
ture, are instead obtained from careful experiments. The measurements are fre-
quently smoothed and fitted to mathematical expressions for use in calculations.
Derived properties such as the energy U or enthalpy H cannot be measured
directly. They are constructed from the mathematical expressions of the measured
properties using the methods described in Chapter 7. Such properties require the
specification of a reference state at which they are arbitrarily set to zero, because
only differences in derived properties between two thermodynamic states can be
obtained the absolute values of derived properties at a single state cannot be
determined and are of no value for making predictions about measurable quanti-
ties.
High quality, evaluated thermodynamic data for many pure components are
now available from online data sources, as described in Appendix I.
Example 2.6 Expansion of gas in a closed system
Consider the piston-cylinder system of Fig. 2.13. The gas is CO2 and the cylinders
cross-sectional area is A = 0.1 m2. The initial temperature is T0 = 300 K and the ini-
tial pressure is P0 = 2 MPa. The mass of the piston is m = 40 kg and the initial height
of the bottom compartment is h0 = 0.20 m. The height of the gas compartment dou-
bles when the piston reaches the top of the tank, h = h0. Calculate the final temper-
ature Tf and pressure Pf , assuming that there is no heat exchange between the in-

terior of the piston and the outside world walls. This assumption is reasonable for
rapid expansion, during which there is not enough time for appreciable heat trans-
fer to occur between the interior and exterior of the cylinder.

We first obtain the molar
density and energy of CO2
at T0 = 300 K, P0 = 2 MPa
from the NIST WebBook:
0 = 895.71 mol/m3
and U0 = 19.260 kJ/mol.
The number of moles of
gas in the cylinder is
Figure 2.13. Piston-cylinder system
N = h0A 0 = 0.20 m 0.1 m2 895.71 mol/m3 = 17.914 mol

A First Law balance between initial and final states gives:
m
U = Q +W = mgh = 40!kg! !9.81! ! !0.20!m!= 78.48!J
s2
!
27
2.5 Properties of Real Fluids
so that
kJ
! !0.078!kJ!=!344.95!kJ
Uf = U0 + U = ! 17.914!mol! !19.260!
mol
U
344.95!kJ
kJ
= 19.256
The final molar energy is: U f = f =

N 17.914!mol
mol
!
The final density is half the initial, f = 0.5895.71 mol/m3 = 447.86 mol/m3.
From the known internal energy and density, an isochoric query of the NIST tables,
with some trial-and-error to find an appropriate temperature range, gives:

Tf = 289.60 K and Pf = 1.0159 MPa

If we had neglected the work term in the First Law balance, we would have ob-
tained Uf = U0 = 19.260 kJ/mol, from which Tf = 289.73 K and Pf = 1.0164 MPa. The
effect of raising the weight of the piston on the final temperature and pressure is
relatively small.
How different would our answer be if we were to assume ideal-gas behavior? The
constant-volume heat capacity of CO2 is CVIG = 28.91 J/(mol k). The final tempera-
!
ture and pressure can be calculated from:
U = NCVIG T Tf = T0
Tf = 300
mgh
NCVIG
= T0
RT0mgh0
PoAh0CVIG
8.314!J/(mol!K)! !300!K! 40!kg! !9.81!m/s2

2106 !J/m3 0.1!m2 28.91!J/(mol!K)
= T0
RT0mg
PoACVIG
= 299.83!K!!
V T
1 299.83
Pf = P0 0 f = 2!MPa
= 0.9994!MPa
Vf T0
2 300
!
The error under the assumption of ideal gases is about 10 K relative to the more
accurate calculation given earlier. The final pressure, on the other hand, is within
2% of the value obtained from accurate volumetric data.
2.6 Problem-Solving Strategies and Additional Examples

Thermodynamics problems can seem quite daunting at first. A common complaint
is that it is not clear how the general principles apply to the specific problem at
hand. In general, one should follow a systematic approach with these steps:
28
1. Draw a schematic diagram of the process and label key quantities.

2. Define the thermodynamic system(s) of interest.
3. State all assumptions.
4. Write down fundamental thermodynamic relationships (e.g. First Law bal-
ance) for the system.
5. Write down constitutive equations (e.g. ideal gas law) or obtain physical
properties from tables. For First Law balances involving ideal gases with
constant heat capacities, it is often useful to set the reference state for the
energy such that U = CVT and H = CPT.
6. Solve the equations using symbols, rather than numerical values, as far
along as it possible.
7. Substitute numerical quantities into the final formula to obtain the an-
swers.
Some examples of applications of this methodology in problems involving First
Law balances follow.
Example 2.7 Underground storage of carbon dioxide
CO2 injection into depleted oil and gas formations underground is a key element of
planned carbon capture and storage activities to mitigate buildup of greenhouse
gases in the atmosphere. Consider CO2 from a pipeline at 150 bar and 20 C being
injected into a formation at P = 20 bar. A concern is that CO2 cools upon depressuri-
zation, leading to formation of hydrates that could block the borehole. You are
asked to (a) calculate the temperature of CO2 after depressurization, (b) determine
to what temperature CO2 should be heated prior to injection so that the tempera-
ture after depressurization is no less than 10 C and (c) calculate the energy re-
quirement of the heating process per mole of CO2 injected.

We will assume that there are no heat
losses (or input) as the CO2 moves
down the injection pipe. In this exam-
ple, the properties of the CO2 for-
mation itself, an open system that is
not at steady state, are not of particu-
lar interest. Instead, the system of in-
terest is the injection pipe and the vi-
cinity of the entrance to the reservoir,
where the pressure drop of the inject-
ed gas takes place. The selection of the
(open) system of interest is shown
with a dashed line the figure.

Figure 2.14. Schematic for Example 2.7

29
(a) A steady-state, open system First Law balance gives:
dU
1 NH
2 H2 = H1
= 0 = Q + W + NH
! dt
where N is the flow rate of CO2 . The enthalpy for P1 = 150 bar, T1 = 20 C can be
found from the NIST chemistry WebBook, using either isothermal or isobaric table
lookup we obtain H1 = 10.926 kJ/mol .
Now we need to find the temperature for which H2 = 10.926 kJ/mol at P2 = 20 bar.
This calls for an isobaric property calculation. This enthalpy is found to corre-
spond to a mixture of saturated liquid and gas at:
T2 = 19.5 C
This is a temperature at which hydrates can indeed form.
(b) The enthalpy at T2 = 10 C, P2 = 20 bar is obtained as H2 = 20.722 kJ/mol. An
isobaric calculation at P1 = 150 bar gives the desired initial temperature to match
this specific enthalpy as:
T1 = 104.4 C
(c) The updated steady-state, open system balance on the pipeline now reads:
dU
1 H 2 ) Q = H 2 H 1
= 0 = Q + W + N(H
N
! dt
Q
= !(!20.722 !10.926)!kJ/mol!=!+!9.796!kJ/mol (heating required)
!N

Example 2.8 Air rifle
A compressed-air rifle operates as follows. The air chamber of volume V0 = 10 cm3
initially contains air at P0 = 3 bar (absolute) and 0 = 25 C. Releasing the trigger ac-
celerates a projectile of mass m = 2 g through the horizontal barrel of cross section
A = 0.3 cm2 and length l = 50 cm.
(a) Calculate the velocity of the projectile as it exits the barrel.
(b) After exiting the barrel, the projectile hits a wall and stops. Calculate its tem-
perature after the impact.
Air can be considered an ideal gas with CV = 20.8 J/(mol K). The projectile has heat
capacity CV = 0.126 J/(g K). The atmosphere is at Patm = 1 bar.
30

Referring to Fig. 2.15, the initial volume of the compressed gas is V0 = 10 cm3; the
final volume just before the projectile has exited the barrel is
Vf = (10 + 0.3 50)!cm 3 = 25!cm 3 .
!
(a) We will assume that there is no heat transfer to or from the gas as it expands
(adiabatic system) and that there is no friction with the walls of the barrel.
We can obtain the final temperature from the relationship between temperature
and volume for adiabatic expansion of an ideal gas, Eq. 2.30:
Tf V
f
=
T V
0
! 0
R
CV
25
Tf = 298!K!
10
8.314
20.8
= !206.6!K
The work performed by the gas can be obtained from a First Law balance between
initial and final states,
U = Q +W W = U = NCV T =
P0V0
RT0
CV T

3105 !Pa!! !10106 !m3
J
!20.8!
(206.6 298)!K!=! 2.30!J
J
mol!K
8.314!
!298!K
mol!K
!
This work is negative because it was produced by the gas on the environment. The
energy goes into increasing the kinetic energy of the projectile and in pushing
back the atmosphere to understand why this term should be taken into account,
consider a firing of the rifle in space; the net force on the projectile would have
been greater in this case, thus resulting in greater final velocity of the projectile.
On earth, a First Law balance for the system projectile + atmosphere gives:

Figure 2.15. Schematic for Example 2.8

31
2!(W + Patm V )
1
E = Q +W = mu2 Patm V u =
2
m
=
!
2!(2.30!J! !10 !Pa! !1510 !m )

m
!=!28.3!
0.002!kg
s
For the system projectile + atmosphere, W = + 2.30 J, as this represents work input.
(b) We will assume here that all the kinetic energy of the projectile is turned into
heat when the projectile hits the wall. Then
1
0.002!kg! !28.32 !m 2 /s 2
U = mCV T = mu2 T =
= 3.18!K
2
2
2!g!
0.126!J/(g!K)

!
Example 2.9 Turbine power generation
A turbine is used to generate power from low-pressure steam obtained from a so-
lar collector at in = 200 C and Pin = 3 bar at a rate of 0.12 kg/s. The outlet of the
turbine is saturated vapor at out = 140 C. If the heat losses of the turbine are 3 kW,
obtain the power (in kW) that the turbine generates.

Steady-state, First Law balance on the turbine gives
dU
= Q + W + N(H in H out ) W = Q + N(H

out H in )
dt
!
Properties are obtained from the NIST WebBook as:
(saturated steam, 140 C) = 2733.4 kJ/kg
!H out
(200 C, 3 bar) = 2865.9 kJ/kg
!H in
kg
kJ
W = +3!kW + 0.12 (2733.4! !2865.9) = !12.9!kW
s
kg

!

Chapter 3. Reversibility and Entropy

We have seen in the previous chapter that systems can move from an initial equi-
librium state to a different final equilibrium state by exchanging heat and work
with their surroundings. A new state can also be generated when a constraint, such
as a barrier to mass or heat flow, is released. The concept of the directionality of
change, however, has not yet been addressed. Everyday experience suggests that
some kinds of processes, even though in full compliance with the First Law, never
occur spontaneously. Examples of spontaneous processes are given in the table be-
low; the reverse processes have never been observed in isolated systems.

Initial state
Final state
Inflated helium balloon
Helium balloon deflated
Two metal blocks in contact

at different temperatures
Two metal blocks in contact

at the same temperature
Sugar crystals at the bottom

of a glass of pure water
Sugar dissolved in the water
Dispersed droplets of oil in water
Oil floating as separate layer on top of

the water

The last two of these examples (sugar dissolving in water, but oil separating
from water) illustrate that it is not always obvious which direction (mixing or de-
mixing) corresponds to spontaneous change. However, once the spontaneous
change direction has been established, it is impossible to convert a system in the
final state column back to the initial state without the action of an external agent.
For example, sugar crystals will not precipitate out of solution unless the water is
evaporated.

36
3.1 Reversibility
37
3.1 Reversibility
Clearly, all processes observed naturally are spontaneous and thus irreversi-
ble. Spontaneous changes define the direction of the arrow of time and are rigor-
ously analyzed through the Second Law of thermodynamics, which is formally in-
troduced in 3.2. By eliminating friction and all gradients of temperature or pres-
sure, and by performing changes at an infinitesimally slow rate, one can approxi-
mate an idealized reversible process. A process in a system going from an initial to
a final state is formally defined as reversible if the system can be brought back to
its initial state from the final state with no change to any part of the universe. Re-
versibility is an idealized abstraction that can be approximated in real processes, if
care is taken to avoid friction, internal or external gradients of temperature, pres-
sure, or composition, as well as any conversion of mechanical work into heat. In
reversible processes, forces
across any boundary exact-
ly balance at all times. Pro-
cesses take an infinitely
long time to complete, be-
cause rates of heat transfer,
macroscopic flow of mate-
rial, and component diffu-
sion are, respectively, pro-

Figure 3.1 Rupture of a partition in an insulated con-
portional to gradients of
tainer.
temperature, pressure, and

chemical potentials (the
latter defined in Chapter 5).
Consider the process schematically illustrated in Fig. 3.1. A thin wall separates
two sides of an insulated container in the initial state (A); the left-hand side con-
tains a gas and the right-hand side is evacuated. The wall is removed and the gas
expands to fill all available space. After some time, the gas reaches a new equilibri-
um state, (B). A First Law balance on the total contents of the container gives U =
Q
/ + W
/ = 0. If the gas is ideal, its energy depends only on the temperature, and T =
0, but this is not an essential characteristic of the process; for real gases, the tem-
perature of state B can be
lower or higher than that
of state A. We can return
the gas to its original state
A by using a piston to
compress it back to the
original volume, as shown
in Fig. 3.2. For this reverse

process, the change of en-
Figure 3.2 Reversing the effect of expansion.
ergy of the gas is the same

38
as previously, U = 0 = Q + W
Q = W ; since we clearly
need to provide work to
compress the gas, the re-
verse process is only pos-
sible if we remove heat
from the system. If some-

how we could convert all
Figure 3.3 Reversible expansion.
of the heat removed into
work, then the overall pro-
cess has no net effect on the environment and would have been reversible accord-
ing to the definition above. However, countless experiments have shown that
complete conversion of heat into work is impossible; we thus conclude that the
original process !A B was indeed irreversible.
We now consider a different process (Fig. 3.3) starting from the same initial
state A as previously, with final state C of the same volume as B. However, we now
perform an adiabatic process (!Q = 0 ), using a well-lubricated, frictionless piston to
obtain work from the expanding gas. The amount of work produced by the gas can
be calculated from:
V
WAC = C P dV
VA
!
Gases generally cool as they expand adiabatically, so that the final tempera-
ture will be TC < TA. For the reverse process of adiabatic compression, we need to
input work, which in the absence of friction will be equal in magnitude and oppo-
site in sign, WCA = WA C. Thus, there is no overall net effect of the process
ACA on either system or its environment. This process is reversible.

3.2 The Second Law of Thermodynamics

The Second Law of thermodynamics places the concept of spontaneous changes on
a rigorous, quantitative basis. It allows for precise predictions about which trans-
formations can or cannot occur naturally in the absence of external driving
forces. It represents, in a highly compact fashion, the accumulated scientific
knowledge gained from countless experiments in carefully constructed systems.
While it cannot be proven from first principles and has to be postulated, it repre-
sents one of the most basic and well-established tenets of modern science.

This, however, is not true for all substances.
3.1 Reversibility
39
The Second Law can be stated in a variety of equivalent ways; in the following,
we use a traditional approach that expresses it in terms of heat fluxes around heat
engines. Heat engines are devices that exchange heat and work with their envi-
ronment in processes that leave no net effects on the engines. An internal combus-
tion engine undergoing a full cycle of compression-ignition-expansion is a classic
example of such a device. However, living cells, photovoltaic arrays, and distilla-
tion columns can also be considered as heat engines, provided that no net changes
accumulate within the devices over the period of interest.
Analysis of heat engines becomes particularly simple if they exchange heat
with heat reservoirs large enough so that their temperature can be considered con-
stant, irrespective of the amount of heat exchanged with the engines. In essence,
this implies that the amount of energy exchanged is small relative to the total heat
capacity of the reservoirs. Practical approximations of heat reservoirs include the
atmosphere, rivers, or the sea, when considered over short enough periods of time
so that their temperature does not vary significantly. Electrical power plants are
usually built near large bodies of water precisely so that they can use them as heat
reservoirs. We will assume that heat reservoirs do not perform, or require, any
work in the process of interest.
The Kelvin-Planck postulate (statement of the Second Law) is that:

It is not possible for a heat engine that interacts with a single heat reservoir to
convert all the heat transferred from the reservoir into work.

In other words, heat cannot be completely converted into work. However, the re-
verse of this process, converting work entirely into heat, is perfectly possible.
Fig. 3.4 depicts a process that is impossible according
to the Kelvin-Planck statement of the Second Law, assum-
ing that the signs of the flows of heat Q and work W are as
indicated by the arrows. If |Q| = |W|, such a device does not

violate the First Law, as a trivial balance around the en-
gine demonstrates. No such device has ever been con- Figure 3.4 An impossible
process.
structed, despite efforts by many people since the dawn

of technological civilization. The practical value of being able to extract useful en-
ergy in the form of electricity or mechanical work by cooling the sea or the atmos-
phere would be enormous; fossil fuel use could then be reduced to zero and a prac-
tically inexhaustible supply of energy would become available to humanity. Na-
ture, however, does not permit such a device ever to function. Even in microscopic
systems, where spontaneous fluctuations occur that seem to result in mechanical
work being produced at the expense of the thermal energy of a reservoir (e.g.
Brownian motion of small particles), the Second Law is found to hold when the av-
erage behavior of a system is determined over long times. Devices that violate the
Kelvin-Planck
statement of
the Second
Law
40
First or Second Laws which thus can never be constructed are called perpetual
motion machines of the first or second kind, respectively.
3.3 Carnot Engines and Absolute Temperature

The seemingly simple statement of
the impossibility of certain process-
es made by the Second Law has
enormous consequences on the be-
havior of natural and engineered
systems. To start analyzing its con-
sequences, consider the behavior of
heat engines operating between two
heat reservoirs of different thermo-
metric temperatures, H and C , as

shown in Fig. 3.5. We will assume Figure 3.5 Thermal engines operating between
that the top reservoir is at a higher two heat reservoirs. Left side (engine A) corre-
sponds to power production and right side
thermometric temperature, H > C.
(engine B) corresponds to refrigeration.
Thermometric temperature in phys-
ical systems is observed to increase as energy flows into them.
On the left side of Fig. 3.5, engine A removes heat from the hot reservoir and
dumps some of it to the cold reservoir, while producing some work. Engine B on
the right panel does the reverse, removing heat from the cold reservoir and dump-
ing it to the hot reservoir through the consumption (input) of work. Nothing in the
First or Second Laws of thermodynamics prohibits any of these processes; practi-
cal examples of such systems, in the form of thermal power generation systems
and refrigeration units are ubiquitous. Nevertheless, there must be some con-
straints in the magnitudes of the work and heat streams from these engines, be-
cause otherwise a combination of them could give rise to a perpetual motion ma-
chine. To see why this is the case, consider using the work output of a machine of
type A to provide the energy input to a machine of type B. Without loss of generali-
ty, we can assume that:

Q = QCB
! CA
This is the case since we can always adjust the size of the heat engine, or how
many engine cycles are performed per unit of time. First Law balance around the
system composed of the engines A+B then gives the net work input as:

The net heat input is:
W = WB WA
!
41
Q = QHA QHB = W
!

If W < 0, then
Q > 0 QHA > QHB

!

Net work is being produced by the two engines by removing heat from the hot res-
ervoir. This is equivalent to a perpetual motion machine of the second kind, violat-
ing the Kelvin-Plank postulate, so it is an impossibility. Therefore, we must have:
W 0 Q 0 QHA QHB
!
for any two heat engines operating between two specific temperatures H and C .
The arguments of the previous paragraph also apply to the special case of re-
versible heat engines, known as Carnot engines. For reversible engines we can
simply switch the role of A and B at will, which gives:

rev
rev
rev
rev

QHA
QHB
!!and!! QHB
QHA
rev
rev

QHA
= QHB
This implies that for any reversible heat engine that operates between H and C

the ratio of heat fluxes is a universal function of the two temperatures:

QHrev
QCrev
= f (H ,C )
!
The specific form of the function in Eq.
3.1 can now be determined, by consider-
ing a cascade of heat engines operating be-
tween a high temperature H, an interme-
diate temperature M and a low tempera-
ture C, as shown in Fig. 3.6. On the left
side, two Carnot engines, 1 and 2, are used
between H and M and between M and

C , respectively. On the right side, a single
engine 3 operates directly between H and
C. We can adjust the heat flows for en-
gines 1 and 2 so that the same amount of
heat is taken and removed from the in-
termediate-temperature reservoir at M,
and we can also adjust engine 3 so that the
same amount of heat is removed from the
hot reservoir as for engine 1. Since these
are Carnot (reversible) engines, we must
have that |W1| + |W2| = |W3|. Therefore, the
(3.1)

Figure 3.6 Thermal engines operating
between three heat reservoirs.
42
same amount of heat is dumped to the cold reservoir on the two sides of the cas-
cade:
QC = QC

QM / f (M ,C ) = QH / f (H ,C )
QH
QH
f (H ,M ) f (M ,C ) = f (H ,C )
f (M ,C ) f (H ,M ) f (H ,C )
!
Since this relationship is valid for any temperatures H, M, and C, the func-
tional form of f must be:

!
g(H )
f (H ,C ) =
g(C )
(3.2)
The function g() is universal for all Carnot engines. Its form can be obtained
from analysis of the operation of any reversible heat engine. When this analysis is
performed for engines that have ideal gases as working fluids (see 4.1), we ob-
tain a particularly simple relationship: g() = T, where T is the temperature that
was defined through the ideal-gas equation of state in 2.4. This remarkable prop-
erty provides a connection between the efficiency of reversible engines and the
ideal-gas temperature scale. The absolute temperature scale T is of fundamental
importance in thermodynamics.
Given that f (H,C) = TH/TC, we can now show that reversible heat flows occur-
ring to and from constant-temperature reservoirs are linked in a particularly sim-
ple way. The heat flows for the cold and hot reservoirs are of opposite signs, so Eq.
3.1 can be expressed as:

QHrev
QCrev
TH
TC
QHrev
TH
QCrev
TC
= 0
(3.3)
The efficiency of a Carnot engine that draws heat from a hot reservoir and
produces work (left side of Fig. 3.5) is defined as the fraction of heat removed from
the hot reservoir that is obtained from the device as work. From a First Law bal-
ance around a reversible engine, we have:

Carnot
Engine
efficiency
T
QHrev + QCrev +W = 0 QHrev C QHrev = W
TH
!
rev
!
W
QHrev
TH TC
TH
(3.4)
43
The efficiency is between 0 and 1, the latter value being a theoretical limit
that can only be asymptotically approached if TC0 or TH+. Real engines, of
course, operate with efficiencies lower than those of reversible engines, since oth-
erwise an irreversible engine could be combined with a Carnot engine operating in
reverse, resulting in a violation of the Second Law. The performance of real en-
gines operating between reservoirs of given temperatures is not the same for all
irreversible engines it varies (sometimes greatly), depending on their design and
internal losses. The reversible engine efficiency provides a common upper limit for
all real engines.
Example 3.1 Efficiency of geothermal power production
In many parts of the world, especially near edges of tectonic plates, relatively high
temperatures can be reached by drilling to moderate depths. Taking advantage of
these high temperatures has been proposed as one possible technology for energy
generation without production of greenhouse gases. Assuming that heat can be
withdrawn from hot rock at H = 200 C and that cooling is available at C = 50 C,
what is the maximum possible fraction of heat removed that can be converted to
electricity?

The maximum possible fraction of heat conversion into work takes place using a
reversible Carnot engine, which has efficiency:
T T
200 50
rev = H C =
= 32%
TH
200 + 273
!
Note that only absolute temperatures [in K] can be used in the expression for ;
however, the difference between two temperatures in C is the same as the corre-
sponding absolute temperature difference in K, so the thermometric temperature
values can be used in the numerator.
For engines operating as refrigeration cycles (right side of Fig. 3.5, p. 40), with
heat removed from the cold reservoir through the net input of work, a measure of
performance different from is appropriate. In such cases, we are interested in
the amount of heat removed from the cold side (the interior of the refrigerator, or
the inside of a building in the case of air conditioning) per unit of work input. The
coefficient of performance, , is:

! = !
!
QC
W
QC
QC QH
rev !=
QCrev
QCrev
T
+ H QCrev
TC
TC
TH TC
(3.5)
Another possibility is the operation of a cycle as a heat pump, to maintain high-

er temperatures inside a building in the winter, by withdrawing heat from the cold
44
outside air. In this case, the coefficient of performance is defined as the ratio of
heat output (into the building) over the work input:
!=!
QH
W
QH
QC QH
rev =
QHrev
T
C QHrev + QHrev
TH
TH
TH TC
(3.6)
The two coefficients of performance defined in Eqs. 3.5 and 3.6 can be greater
than 1, if the difference between hot and cold temperatures is smaller than the ab-
solute value of the cold or hot temperature, respectively. Practical power and re-
frigeration cycles are discussed in Chapter 4.
Example 3.2 Air conditioner theoretical efficiency
Calculate the maximum possible coefficient of performance for an air conditioning
unit operating between an indoor temperature of 68 F and outdoor temperature
of 104 F.

We first need to convert thermometric to absolute temperatures: C = 68 F C =
293 K; C = 104 F TH = 313 K. The maximum possible coefficient of performance
is:
rev
!=!
QCrev
W
TC
TH TC
293
= 14.6
313 293
3.4 Entropy Changes in Closed Systems

We showed in the previous section that reversible heat flows occurring to and
from constant-temperature reservoirs satisfy the condition QHrev /TH + QCrev /TC = 0 ;
!
this in turn suggests that a heat-related property can be defined that is conserved
for a system undergoing a reversible process that starts and ends at the same state
point. This new property is called the entropy S. For a reversible process in closed
systems for which all exchange of heat is done at a single temperature T, the en-
tropy change S is defined as:
Q rev
S

(3.7)
T
!
For a differential change of state during a reversible process, the temperature
of the system is effectively constant, so we can write:

Q rev
dS =

T
!
(3.8)
45
The overall entropy change for a general process that involves temperature
changes along its path is:
definition of
entropy
rev
B Q

S = SB S A =
A T
!
(3.9)
A reversible process can always be constructed between any two equilibrium

states of a system, provided that external reservoirs are available to exchange heat
and work as needed. Thus, Eq. 3.9, along with a choice of a reference state for
which S = 0, in principle provides a way to generate values for the entropy of any
equilibrium state of a thermodynamic system. As will soon become apparent, Eq.
3.9 is not usually a practical approach to obtain actual entropy changes. Thermo-
dynamic relationships incorporating volumetric and heat capacity data, to be dis-
cussed later in the present section and in 7.3, are more commonly used for en-
tropy change calculations.
A key property of the entropy is that it always increases for spontaneous pro-
cesses in closed, isolated systems. This property is often used as an alternative
statement of the Second Law
here, we simply derive it from the
Kelvin-Planck postulate as follows.
Consider an irreversible, adiabatic
process taking place between ini-
tial state A and final state D, along
the dashed-line path of Fig. 3.7.
Curves AB and CD represent re-
versible adiabatic paths from the
initial and final state respectively,
and curve BC is an isothermal path

at temperature T. For the reversible
Figure 3.7 Pressure-volume relationship for ir-
process DCBA that brings the sys-
reversible process (dotted line) and adiabatic-
tem from state D back to the initial
isothermal-adiabatic path.
state A, all heat transfer takes place
along the isothermal step BC, so that:
rev
rev
rev

U UD = QDA
+WDA
= T(S A SD )+WDA
! A
For the irreversible process AD
irr

U U A = WAD
! D
Adding these two expressions we obtain
rev
irr
T(S S )+WDA
+WAD
= 0
! A D
46
irr
rev
rev
+WDA
< 0 , then T(S A SD ) = QDA
> 0 ; the overall cycle has received
If WAD
!
!
!
heat input from a single reservoir at T and has produced net work. This is a viola-
tion of the Kelvin-Planck postulate and therefore impossible. The case
rev
W irr +WDA
= 0 implies that T(S A SD ) = Q rev = 0 and the final state could be re-
! AD
!

turned to the initial state with no net effect on the environment; this contradicts
the original statement that the process AD was irreversible. Therefore, we must
have, for any irreversible process in an isolated closed system from state AD,
T(S A SD ) < 0 , or equivalently:
S > S [for irreversible process A D]

!D A
(3.10)
irr
rev
irr
rev
+WDA
> 0 WAD
> WDA
In addition, we must have WAD
. By changing the
!
direction of the reversible process from DA to AD we then obtain:
rev
W irr > WAD
!!
! AD
(3.11)
Since the universe can be considered a closed isolated system, Eq. 3.10 is the
mathematical equivalent of the Clausius statement of the Second Law, the entropy
of the universe tends to a maximum. Eq. 3.11 states that the algebraic work
amount is always greater for an irreversible process. If the reversible process re-
rev
!>!0! ) then the irreversible process requires more work input;
quires work ( WAD
!
rev
!<!0! ), Eq. 3.11 suggests that the ir-
if the reversible process produces work ( WAD
!
reversible process will produce less work it may even require work input! Re-
versible processes are the best of all possible processes in achieving a given task
with the least expenditure of useful work and in extracting the maximum possible
amount of useful work out of a given change of state.
Entropy has been just derived from analysis of heat and work flows in reversi-
ble heat engines; however, once it has been established that entropy is a proper
thermodynamic function, it can be expressed for any equilibrium state in terms of
any convenient thermodynamic variables. This provides the starting point for de-
velopment of thermodynamic identities through the formal approach described in
Chapter 5. Let us take a look again at the differential form of the First Law of ther-
modynamics, written for a closed system undergoing a reversible process:

rev
rev
!dU = Q + W
(3.12)
A differential change of state does not substantially change the temperature of

the system, so we can set Q rev = TdS . Since the pressure also remains constant
!
(within a differential amount), the work performed by the environment on the sys-
tem can be expressed as !W rev = PdV . Combining the expressions for Q rev and
!
rev
!W we get the fundamental equation of thermodynamics, which provides a syn-
thesis of the First and Second Laws:
47
!dU = TdS PdV
(3.13)
Eq. 3.13 has only proper thermodynamic state functions on both sides, contain-
ing no inexact differentials involving heat or work amounts. Changes in state func-
tions are independent of the path, so the equation is valid for all processes, re-
versible or irreversible. In irreversible processes, the first term (TdS ) is not equal
to the amount of heat, and the second term, (PdV ) does not equal the amount of
work; but their sum still gives the change in system energy.
Example 3.3 Entropy change for an ideal gas
10 mol of an ideal gas with CV = 20.8 J/mol at T0 = 300 K and P0 = 0.3 MPa occupy
the left half of an insulated vessel, as shown in Fig. 3.8. The other half is evacuated.
At time t = 0, a 1 kW electrical heating element is turned on. After 30 s, the parti-
tion dividing the vessel ruptures and the heating element is turned off. Calculate
(a) the final temperature Tf and pressure Pf of the gas in the vessel and (b) the en-
tropy change of the gas during this process.

The final temperature of the gas can be obtained from a First Law balance on the
contents of the vessel:
U = NCV T = Q + W Tf = T0 +
Q
NCV
30!s! !1000!J/s
Tf = 300!K! +
= 444!K
10!mol! 20.8!J/(mol!K)
!
The final pressure is obtained from the ideal-gas law,
Pf Vf
RTf
P0V0
RT0
Pf = P0
V0Tf
Vf T0
444!K
Pf = 0.3!MPa
= !0.222!MPa
2! !300!K
!
The entropy change cannot be directly obtained from
the definition (Eq. 3.9), as this is not a reversible pro-
cess. Instead, it can be obtained from Eq. 3.13:

Figure 3.8 Schematic of pro-
cess for Example 3.3.
1
P
dU = TdS PdV dS = dU + dV
T
T
!
NCV
C
T
V
NR
S
R
dS =
dT +
dV
= V dT + dV = CV ln f + Rln f
T
V
N
T
V
T0
V0
!
Valid for
any process
in a closed
system
48
S
444
J
J
= 20.8ln
+ 8.314ln2 !
= (8.16 +5.76)!

N
300
mol!K
mol!K
J
J
S = 10!mol! 13.9
S = 139!
mol!K
K
!
!
The entropy change is, of course, greater than zero during this irreversible pro-
cess.
Using the same approach as in Example 3.3, it is easy to prove that the general
relationship for the entropy change of an ideal gas with temperature-independent
heat capacities during a process that takes it from (T0 ,P0 ,V 0 ) (Tf ,Pf ,V f ) is:
Entropy
change for
an ideal gas
S
!
IG
= CV ln
Tf
T0
+ Rln
Vf
V0
= C P ln
Tf
T0
Rln
Pf
P0
(3.14)
Eq. 3.14 is of general applicability to changes of state for ideal gases the pro-
cess does not have to be reversible, at constant temperature or at constant pres-
sure.
Example 3.4 Forging
A common process in metallurgy is to immerse a red-hot item (e.g. a blade being
forged) in water to harden it. Let us consider a process in which a 1 kg steel blade
at 1 = 800 C is immersed in a large vessel filled with water at 2 = 25 C and imme-
diately quenched. Assuming that steel has heat capacity CV = 460 J/(kg K), inde-
pendent of temperature, calculate the entropy changes during this process of (a)
the steel blade, (b) the water, and (c) the universe. Assume that there is enough
water in the vessel so that its temperature does not increase appreciably during
the process of immersion.

The entropy change of the steel blade in this irreversible process can be calculated
from Eq. 3.13, ignoring the small volume change of the solid as it cools down:
dU = TdS PdV
!
NC dT
1
dS = dU = V

T
T
C
T
Sblade = N V dT = NCV ln f
T
T0
!
J
273+ 25
J
Sblade = 1!kg! !460!
!ln
= 589!
kg!K 273+ 800
K
!
49
Even though this is an irreversible process, the blades entropy goes down the
blade is not an isolated system, so Eq. 3.10 does not apply.
For the water, we are not given enough information to calculate its temperature
change; since the process is clearly irreversible, it would seem that we cannot use
the definition of entropy change (Eq. 3.9) however, this is not true! Even though
the overall process is irreversible because of the large temperature difference be-
tween the blade and the water, we can devise a thought experiment in which the
heat transfer to the water is done in a reversible manner. The amount of heat
transferred is:
J
Q = U blade = NCV T = 1!kg 460!
(25 800)!K!=!356!kJ
kg!K
!
The entropy change for the water in a reversible process with the same Q is:
Q rev
356!kJ
J
Swater =
=
= 1196!
T
(273+ 25)!K
K
!
The entropy change of the universe is:
J
J
Suniverse = Swater + Sblade = (589+1196) = +607
K
K
!
Once again, the entropy change of the universe is positive, as it should be for an
overall irreversible process.
3.5 Entropy Changes in Open Systems

The entropy of an open system can change because of heat exchanged with the en-
vironment, because of flows into and out of the system and because of entropy
generation due to internal irreversibilities entropy is not a conserved quantity!
While entropy can be created, a process can never result in a net decrease in the
entropy of the universe; this would violate the Second Law of thermodynamics.
This condition translates into an inequality linking the entropy change of the sys-
tem Ssystem, the entropy change of the environment Senv, and the specific entro-
pies of entering and leaving streams:

Suniverse = Ssystem + Senv +

!
leaving
streams
Nout S out
entering
streams
Nin S in 0 (3.15)
Why are the terms for the entering and leaving streams in Eq. 3.15 of opposite
sign relative to Eqs. 2.16 or 2.19 (p. 18), the First Law balance for open systems?
50
Eqs. 2.16 and 2.19 are written from the point of view of the system, which gains
the streams that enter and loses the streams that leave. By contrast, Eq. 3.15 rep-
resents a balance for the entropy of the universe. For the universe, streams enter-
ing the system are lost and streams exiting the system are gained. A similar re-
lationship can also be written as a differential (rate of change):

Suniverse = Ssystem + Senv +
leaving
streams
N out S out
entering
streams
N in S in 0
(3.16)
For reversible processes, Eqs. 3.15-3.16 become equalities, with their right-
hand side equal to zero. For other special cases, specific terms can be set to zero,
significantly simplifying the equations. For example, the term Ssystem is zero at
steady state, as there is no net change in the system. Another example of simplifi-
cation is for an adiabatic process, for which we can set Senv = 0, since no heat flows

into the environment.
The fact that entropy generation is non-negative for all feasible processes im-
poses significant constraints on the amount of work that can be produced from (or
is required for) specific processes. When performing a thermodynamic analysis, a
typical approach is to apply in turn a First Law balance followed by a Second Law
balance, as illustrated in the examples that follow.
Example 3.5 Feasibility of a process
An inventor is proposing a black box device for producing electrical power that
operates on a stream of compressed air at P1 = 4 bar, T1 = 300 K. The input stream is
split into two equal flows of P2 = P3 = 1 bar at T2 = 280 K and T3 = 260 K, respectively.
The claim is made that power is produced at a steady-state rate of W = 3.4 kJ/mol
of air flowing through the device. Assuming that unlimited heat exchange with the
environment at Tenv = 300 K is allowed, you are asked to provide an analysis of the
thermodynamic feasibility of such a device. Assume that air can be approximated
as an ideal gas with CP = 29.1 J /(mol K), independent of temperature.

First, we apply an integral
First Law balance on this
open system over the pe-
riod of time it takes for 1
mol of air to flow through
the device, which is as-
sumed to be at steady
state. The flow of streams
2 and 3 is half the flow of
stream 1. We use a refer-
ence state for the enthalpy
Figure 3.9 Schematic of process for Example 3.5.

51
such that H = C PT .
U
= 0 = Q +W + NH 1
!steady!state
T +T
N
N
H 2 H 3 Q = W NC P T1 2 3
2
2
2
J
260+ 280
Q = (3400)!J! 1!mol!
!
!29.1!
300
K != 2527!J
mol!K
2
!

Since the heat calculated from the systems point of view is positive, heat flows
from the environment to the system during this process. We must now check
whether the entropy generation rate for the universe is non-negative. We use Eq.
3.14 (p. 48) to calculate the entropy change of the ideal gas streams and take into
account that the flow of heat into the environment is the opposite of the value cal-
culated from First Law balance on the system:
Suniverse =
Sdevice + Senv + Nout S out Nin S in =
leaving!
entering!
steady!state
!
= !
streams
streams
Q N
N
Q N
+ S 2 + S 3 N S1 =
+ (S 2 S 1 + S 3 S 1 )
Tenv 2
2
Tenv 2
TT
PP
Q N
+ C P ln 2 3 Rln 2 3 =
Tenv 2
T12
P12
2527!J 1!mol
J
260 280
J
1
!+!
29.1!
ln
8.314
ln 2 =
2
300!K
2
mol!K
mol!K 4
300
J
J
!!!!!!!!!!!!!!!!!!!!!!!!!!! 8.42 3.09!+11.53 ! = +0.02!
K
K
!
The entropy change of the universe is positive, so operation of the device is possi-
ble as described. However, since the entropy change is small relative to the terms
of which it consists, the device is operating near the thermodynamic limit for re-
versible processes.

Example 3.6 Solar power generation
Solar collectors are used to heat, continuously and at steady state, a molten salt
stream from 200 C to 600 C at a flow rate of 12 kg/s. The hot stream generates
electrical power by a complex process and then returns to the solar collectors.
What is the maximum amount of power that can be produced? Assume that the
environment is at 20 C. The heat capacity of the molten salt at constant pressure is
CP = 0.8 kJ/(kg K), independent of temperature.
52

The system of interest is the power plant that
uses the salt stream. We label the

hot stream H and the cold one C. An open-system First Law balance for this sys-
tem gives:
dU
=0
dt
H HC )
= Q + W + N(H

steady!state
W = Q + NC P (TC TH )
!
The maximum amount of work is produced in a reversible process, for which
Suniverse = 0 =
Splant + Senv + Nout S out Nin S in =
leaving!
entering!
steady!state
streams
streams
T C
T
Q
ln C
+ N(S C SH ) Q = Tenv N C P dT = Tenv NC
P
T
Tenv
TH
H T
T
T ln H +T T
W = NC
P
env
C
H
TC
273+ 600
kg
kJ
W = 12 0.8
293!ln
+ 200 600 K!!= 2.12!MW
s
kg!K
273+ 200
!
The power is negative because it is being produced by the power plant.
Example 3.7 Analysis of a Steam Turbine

A power plant operates with supercritical steam at T1 = 900 K and P1 = 8 MPa as in-
put to a turbine. The steam exits at T2 = 430 K. Assuming that the turbine operates
53
reversibly and adiabatically, how much steam is required to generate power at a

rate of 1 MW?


For reversible operation of the steam turbine, we must have:
Suniverse = 0 = Sturbine + Senv + N(S 2 S 1 ) S 2 = S 1
reversible!process
steady!state
adiabatic
The properties of steam at the entrance of the turbine (T1 = 900 K and P1 = 8 MPa)
can be obtained from the NIST WebBook as follows:
kJ
kJ
H 1 = 3707! !!!!!S 1 = 7.095

kg
kg!K
!
We now need to find the pressure for which S2 = S1 = 7.095 kJ/(kg K) at T2 = 430 K.
With a bit of trial-and-error with respect to the pressure range, we can obtain from
the NIST WebBook P2 = 0.31 MPa, H2 = 2775 kJ/kg. A First Law balance on the tur-
bine now gives:
dU
= 0 = Q + W + N(H
1 H2 )
dT
!steady!state
W
103 !kJ/s
N =
=
H 2 H 1 (2775 3707)!!kJ/kg
!
Example 3.8 Work for evacuating a tank
kg
N = 1.073
s
!

A tank of volume V0 initially contains air at a certain temperature T0 and pressure

P0. The environment is also air at T0 and P0. Obtain general expressions for the
minimum amount of work required to evacuate or compress the tank to a pressure
P1 = P0 (a) isothermally and (b) adiabatically. Perform illustrative calculations for
= 0.1 and 10, and obtain the work required for complete evacuation ( = 0). Air
can be considered an ideal gas with CV = 5R/2.

54
This problem can be handled most conveniently

by transformation from an open to an equivalent
closed system. For the case of evacuation, we
would like to remove material from the tank of
volume V0 , initially at T0 and P0, to bring the pres-
sure down to P1. This process reduces the number
of moles in the tank from N0 to N1. Instead of ac-
complishing this by action of a pump, in the
Figure 3.12 Schematic of pro-
closed system process, a frictionless piston is set
cess for Example 3.8.
up as shown in Fig. 3.12, at a position within the
tank that contains an amount of material N1, has
volume V1, and is originally at T0 and P0. At the right-hand side of the piston there
is air at T0 and P0. We will pick V1 so that after the piston has moved from V1 to V0,
the final pressure within the tank is P1 = P0. This reversible process accomplishes
the same task as pumping the original tank (of volume V0) from P0 to P1. The mini-
mum work for evacuation is obtained as the work to move the piston rightward
from V1 to V0. A similar approach can give the minimum work required for com-
pression to a certain pressure, or the maximum work that can be obtained from a
cylinder of compressed air.
(a) Isothermal operation
For this case, from the ideal-gas equation-of-state, PV = NRT, the volume V1 is ob-
tained as:

V1
V
! 0
P1
P0
N1
N0
The instantaneous pressure difference across the piston is P P0, where P is the
pressure within the expanding volume on the left side. The total work required to
move the piston to the right is:
V
V0 N RT
1
V1
V1
W = 0 (P P0 )dV =
dV + P0(V0 V1 ) = N1RT ln
V1
V0
+ P0(V0 V1 )
V PV PV
P V
W N1
=
RT ln 1 + 0 0 0 1 = RT ln + RT 0 1 = RT ln + RT RT
N0 N0
V0 N0
N0
N1
W
W
=
= ln +1
RTN0 P0V0
For = 0.1, this equation gives W/(RTN0) = 0.670.

Because ln0 as 0, the expression has a simple interpretation at the limit of
complete evacuation:
55
W
W
=
= 1 W = P0V0 for complete evacuation.
!
N0RT P0V0
!
In other words, the minimum work for complete evacuation is the work to push
back the atmosphere by a volume equal to the original tank volume.
n the case of pressurization, a more meaningful measure than the work per mole
initially in the tank is the work per mole of compressed air, obtained by dividing
the full expression above by = N1/N0,
W
W
1
=
= ln + 1
RTN1 P1V0
For = 10, this equation gives W/(RTN1) = 1.403. The work required is positive
(work input to the system) for both lowering and increasing the tank pressure to a
value different than atmospheric.
(b) Adiabatic operation
Here, we will use the expressions obtained in 2.4 for adiabatic compression and
expansion of an ideal gas. Even though we did not state so at the time, adiabatic
operation (Q = 0) at internal equilibrium implies also a reversible operation, since
the entropy change of the universe for such a process is zero.
As previously, we find V1 so that P1 = P0 after expansion. From Eq. 2.31, with ini-
tial volume and pressure V1 and P0 and final values V0 and P1 :
V
== 0
P
V1
! 0
P1
V1
V0
= 1/ =
CV /C P
The final temperature after expansion is obtained from Eq. 2.30:

1
P
R/C
= 1 = P
T
P
! 0 0
The work performed on the gas during the expansion is, from Eq. 2.32:
T1
T
R/C
Ugas = Q +Wgas Wgas = N1CV T = N1CV (T1 T0 ) = N1T1CV 1 0 = N1T1CV 1 P
T1
!
The net work required is the sum of the work performed on the gas and the work
to push back the atmosphere,
56
W = Wgas + P0 (V0 V1 ) = N1T1CV 1
R/C P
) + P (V V )
0
N1T1CV
PV
PV
PV C
W
R/C P
=
1
+ 0 0 0 1 = 1 0 V
N0RT0
N0RT0
N0RT0 N0RT0
P0V0R
W
W
1/
=
=
+1 1/
RT0N0 P0V0
1
V
1 +1 1
V0
For air, =7/5=1.4, so that for = 0.1 we obtain W/(RTN0) = 0.574. A little less
work is required for adiabatic evacuation than for isothermal one. At the limit
0, this expression also gives W = P0V0, as for the isothermal case.
For adiabatic pressurization, the work per mole of compressed air is:
1/
W
W V0 W
W
11/ 1
1/
=
=
=
+11/
=
+ 1/ 1
RT N
1
RT N P V V1 RT0N0
1
! 0 1
! 0 1 1 0
For = 10, this expression gives W / (RTN1) = 1.520, a little more than in the iso-
thermal case.
3.6 Microscopic Origin of Entropy

By this point, we are familiar with the definition of entropy from a macroscopic
thermodynamic viewpoint as S = Qrev/T. But what is the origin of entropy in the
microscopic, molecular world? Qualitatively, we expect that irreversible processes
(which result in an increase in total entropy) also increase the degree of disorder
in a system. It turns out that a quantitative measure of disorder, specifically the
number of microscopic states available to a system at a given internal energy U
and for specified number of molecules (or moles) N and volume V, can be quantita-
tively linked to the entropy. A distinct microscopic state (microstate) is defined by
all microscopic degrees of freedom e.g. positions and velocities of molecules in a
gas. A set of microstates with specified common properties (e.g. number of parti-
cles N, volume V and energy U) defines an ensemble. The expression of S in terms of
microstates is provided by the famous 1872 entropy formula of Ludwig Boltz-
mann,
S = kB ln (N ,V ,U )
!
(3.17)
Boltzmanns entropy formula is the foundation of statistical mechanics, con-

necting macroscopic and microscopic points of view. It allows calculations of mac-
roscopic thermodynamic properties by determining properties of microscopic
57
configurations. The constant kB is called Boltzmanns constant; it is the ratio of the

ideal-gas constant to Avogadros number, or equivalently the gas constant on a per
molecule basis: kB = R/NA =1.3806510-23 J/K.
To illustrate the concept of counting microstates, we will use the simple sys-
tem shown in Fig. 3.13. In the general case, it consists of N slots, each containing a
ball that can be at energy levels 0, +1, +2, +3, , measured in units of kBT0, where
T0 is a reference temperature. The specific case of N = 10 and 3 energy levels is
shown in the figure. The concept of discrete energy levels arises very naturally in
quantum mechanics. For this simple system, we can count states by using the
combinatorial formula giving the number of ways we can pick M specific distin-
guishable objects out of N total objects:
N
N!
N (N 1)(N M +1)

(3.18)
= M!(N M)! =
12M
M
!

There is only 1 state with internal energy U = 0. States with U = 1 have one ball
at level +1 and the others at level 0, so for N = 10, there are 10 such states. States
with energy U = 2 may have 1 ball at +2 and the others at 0, or 2 balls at +1, so there
are:
10

+10 = 55
2
!
such states. We can similarly obtain (3 )= 220; (4 )= 715, (5 )= 2002, and so
on. Note that the number of microstates increases rapidly with the total energy of
the system. This is generally the case for most systems.
Now we are in a position to show that S defined microscopically from Eq. 3.17
has the two key properties associated with the entropy of classical thermodynam-
ics:
1.
S is extensive: For two independent subsystems, A and B,
S = k ln( A+B ) = kB ln( A B ) = kB ln A + kB lnB

! A+B B
The reason is that each microstate of system A can be combined with a
microstate of system B to give a microstate of the combined system. This is
clearly true for the simple system illustrated on the previous page. However,
when mixing two
gases or liquids, we
only get the above
expression if we
assume that the
particles in the

systems
are Figure 3.13 A system of 10 spheres with 3 energy levels.
indistinguishable. If

58
particles are distinguishable, additional states are available to the combined

system resulting from the possibility of exchanging the labels of particles.
Although the indistinguishability of particles is really of quantum mechanical
origin, it was introduced ad hoc by Gibbs before the development of
quantum mechanics, in order to make entropy an extensive property.
2.
S is maximized at equilibrium: For a system with internal constraints (e.g.

internal rigid walls or barriers to energy transfer), the number of possible
microstates is always smaller than the number of microstates after the
constraints are removed.
S (N,V, U) > S (N,V, U; internal constraints)

To demonstrate this second property, consider the box with particles of the
example above, and think of any constraint to the system at a given total
energy (say U=+2). An example of a "constraint" would be to have that the
first five slots have exactly 1 unit of energy. The number of microstates in
this case is (5x5=25), less than the 55 states available to the unconstrained
system.
One clear distinction between macroscopic and microscopic definitions of en-

tropy is that the former is physically meaningful only as a difference of entropy be-
tween specified states, while the latter appears to provide a measure of absolute
entropy. This apparent discrepancy results from the inability of classical physics to
define uniquely when two nearby states (e.g. positions of a particle in free space
differing by a fraction of a nm) are sufficiently different to justify distinguishing
them from each other. Quantum mechanical methods, on the other hand, provide
precise ways to count states.
At low temperatures, the number of microstates available to any physical sys-
tem decreases rapidly. At the limit of absolute zero temperature, T 0 , most sys-
tems adopt a unique ground state for which = 1 S = kBln = 0. This is the basis
of the Third Law of thermodynamics postulated by Nerst in the early 1900s. The
NIST Chemistry WebBook lists absolute entropies for pure components and chem-
ical elements in the thermochemistry data section. However, using entropy values
calculated with respect to an arbitrary reference state gives the same results as
absolute entropies for heat and work amounts.
Example 3.9 Entropy of a lattice chain
A common model for polymers is the Flory lattice model, which represents chains
as self-avoiding random walks on a lattice (grid). Self-avoiding means that two
beads cannot occupy the same position on the lattice. When two non-bonded
beads occupy adjacent positions, they have energy of interaction equal to kBT0,
where T0 is a reference temperature. Obtain the number of microstates for a
two-dimensional square-lattice chain of 5 beads, as a function of the energy U of
the chain.
59

Fig. 3.14 shows the number of configurations for a square-lattice chain of 5 beads.
Without loss of generality, we have fixed the configuration of the first two beads of
the chain to be in the horizontal direction, with the second bead to the right of the
first. This reduces the total number of configurations by a factor of 4; such a multi-
plicative factor simply shifts the value of S obtained from Eq. 3.17 by a constant
factor, akin to the reference state for the entropy. The last bond is shown in multi-
ple configurations (arrows), along with their number and energy: !2(1) for the
top left image means there are 2 configurations, each of energy 1.
Overall, counting configurations of the same energy:
(U=0) = 3+2+2+3+2+2+3=17 ; (U=1) = 2+1+1+1+1+2=8
The number of microscopic configurations and energy levels increases rapidly
with chain length. Theoretical and Monte Carlo computer simulation techniques
are used for determining the properties of models of this type for longer chains.

Figure 3.14 Configurations for a two-dimensional chain of 5 beads

A key issue in statistical mechanics is the frequency of occurrence of different

microstates when the overall constraints of a thermodynamic system are specified.
A basic postulate, comparable in importance to the postulate about the existence
of equilibrium states in classical thermodynamics discussed in 1.4 (p. 6), is that
all microstates of a system at a given U, N and V are equally probable. The conse-
quences of this postulate will be fully explored in Chapter 5.
60
The basic postulate of statistical mechanics implies that the probability of any
microstate , P , is the same as that of any other microstate in the constant N ,V ,U
ensemble:
1

P = at constant N, V and U
(3.19)
!
From this postulate, we can now simply derive another famous expression, the
Gibbs entropy formula, by substituting Eq. 3.19 into Eq. 3.17:

Gibbs
entropy
formula
S = kB
!
P lnP
(3.20)
all!micro+
states!
The Gibbs entropy formula can be shown to be valid even for systems not at
constant energy U, volume V, and number of particles N. This is in contrast to Eq.
3.17, which is only valid at constant for microstates at constant U V and N. For ex-
ample, in 5.6 we prove Eq. 3.20 for systems at constant N, V, and T.

Chapter 4. Fundamental Equations

Two key problems in thermodynamics are to relate properties to each other and to
develop ways to measure them accurately in the laboratory. For example, we have
seen in Chapter 2 that the relationship between the heat capacities at constant
volume and at constant pressure for an ideal gas is:
C IG = CVIG + R
! P
It is highly desirable to obtain a general relationship between the two heat capaci-
ties,

C = (U / T )V and C P = (H / T )P ,

! V
!
for non-ideal gases, liquids and solids. In the present chapter, we develop a formal
approach that allows us to obtain such relationships between thermodynamic de-
rivatives in a systematic fashion.
An important consideration in developing thermodynamic relationships and
methods for determining derived thermodynamic functions such as the energy,
enthalpy, or entropy, is the preservation of information content as one moves
from one function to another. In the rest of this chapter, we demonstrate how all
these functions, when expressed in terms of their natural variables, are essential-
ly equivalent to each other and encompass all available information about equilib-
rium states of a system. These equivalent, complete descriptions of thermodynam-
ic properties are called fundamental equations and are the main topic of the pre-
sent chapter.
4.1 Thermodynamic Calculus

As already mentioned in Chapter 1, for a given quantity of a one-component sys-
tem at equilibrium, all properties are completely determined by specifying the
values of two additional independent thermodynamic variables. More generally,
n+2 independent thermodynamic variables, where n is the number of components
in a system, are needed to fully characterize equilibrium states for multicompo-
nent systems. Common thermodynamic variables used to specify equilibrium

Draft material from Statistical Thermodynamics, (2012), A.Z. Panagiotopoulos
79
80
states in such systems are the total volume V, number of moles of each component,
N1, N2, Nn, temperature T and pressure P. The total entropy S can also be specified
and controlled with some effort, namely by performing reversible processes and
using the definition developed in Ch. 3,

to measure entropy changes.
S = Q rev /T
!
It is clear from empirical observations that not all combinations of variables

result in a unique specification of the state of thermodynamic systems. This is es-
pecially apparent when the possibility of coexistence between phases of different
properties is taken into account. For example, at a given temperature and at the
saturation pressure in a one-component system, there are infinitely many ways in
which two phases can coexist as equilibrium thermodynamic states differing in the
relative amounts of the two phases. In other words, specifying the pressure and
temperature at vapor-liquid equilibrium of a pure fluid does not uniquely specify
the relative amounts of liquid and vapor. Similarly, a given pressure and volume
(or density) of a binary mixture can be realized in many different ways for a range
of temperatures in a two-phase system. In addition to the issue of the uniqueness
of thermodynamic states, certain privileged sets of variables are natural for spe-
cific properties. Thermodynamic functions expressed in their natural variables
contain more complete information than the same properties expressed in other
sets of variables. In order to explain why this is the case, let us consider the com-
bined statement of the First and Second Laws for closed systems derived in 3.4:
!dU = TdS PdV
(4.1)
This expression suggests that the volume and entropy constitute a good set of
variables for describing the energy U of a closed system. More formally, we write:
U
U
U = U(S,V ) dU =
dS +
dV
S V
V S
!
(4.2)
The derivatives are identified as:
U
U
S = T and V = P
S
!
!
(4.3)
To obtain the full expression for U as a function also of the amount of material
in a system in addition to S and V, we need to augment Eq. 4.2 by additional varia-
bles, namely the amount of material of each component present in the system. For
this purpose, we define an additional partial derivative, written here for a one-
component system:
81
U

(4.4)

N S ,V
!
This derivative defines an important new thermodynamic variable, the chemi-
cal potential of a component. The chemical potential is an intensive variable that
has units of specific energy, [J/mol]. Its physical interpretation in classical thermo-
dynamics is somewhat obscure when compared to the two other more intuitively
understood first-order derivatives of the energy function given by Eqs. 4.3. How-
ever, the chemical potential plays just as fundamental a role in thermodynamics as
temperature and pressure.

An example of a relatively simple instrument that measures chemical poten-

tials is the pH meter, which many of us have used in chemistry laboratories. The
instrument measures the chemical potential of hydrogen ions, not their concentra-
tion. Of course, the two are related, with the chemical potential increasing with
increasing concentration but there is a clear distinction. After all, density also
increases with pressure, but pressure and density are not usually confused to be
the same physical quantity! Another way to develop a physical feeling for the
chemical potential is to consider your senses of smell and taste. What exactly is
being measured when you find that a food tastes sour, or when you smell a fra-
grance from a flower? One may naively suggest that it is the concentration of the
molecules that correlates with the intensity of taste and smell, but in reality it is
the chemical potential of the corresponding components that drives the biochemi-
cal receptors responsible for these senses. In addition to chemical reactions, diffu-
sion and evaporation are also driven by chemical potential (not concentration)
differences. On a hot and humid summer day, sweating does not cool you down
because there are no chemical potential differences to drive evaporation, despite
the large concentration difference for water between wet skin and air.
Using the newly defined derivative of Eq. 4.4, we can now write a complete dif-
ferential relationship for the energy as a function of entropy, volume and number
of moles, U = U (S,V,N):
!dU = TdS PdV + dN
(4.5)
More generally, for a multicomponent system, one needs n+2 variables to fully
characterize the state of a system. When the function of interest is the total energy
U, these variables can be selected to be the total entropy, S, volume, V and amount
of moles for each component present, {N} N1 ,N2 ,Nn :
dU = TdS PdV + i dNi

i=1

!
(4.6)
The chemical potential i of a component in a mixture is defined from a direct

extension of Eq. 4.4,
funda-
mental
equation
82
U

i
Ni S ,V ,N
ji
!
(4.7)
In this equation, Nji indicates that the number of moles of all components other
than i are kept constant; more explicitly, N1 ,N2 , Ni1 ,Ni+1, Nn are constant while
Ni varies. Because the chemical potential definition implies an open system to
which a component is added, its value depends on the reference state for energy
for the corresponding component and thus is not directly measurable, unlike the
first two derivatives of Eq. 4.6, temperature and pressure.
Eq. 4.6 is the single most important equation of this book and is known as the
fundamental equation of thermodynamics (abbreviated FE). It links the key quan-
tities of the First and Second Laws and provides the starting point for understand-
ing equilibrium and stability as well as for deriving thermodynamic relations. S, V
and {N}, the variables in which the function U is expressed in this representation,
are all extensive, proportional to system size (mass). The first derivatives, T, P and
i's are all intensive, independent of system size. An equivalent representation of
the entropy S as a function S (U ,V ,N1 ,N2 , Nn) can be obtained by rearrangement
of the terms of Eq. 4.6:
n
1
P
dS = dU + dV i dN i
T
T
i=1 T
!
(4.8)
This representation of the fundamental equation is used in statistical mechanics.

Example 4.1
The fundamental equation for a pure substance is
aUV bN 3

S=
N
UV
!
where a and b are positive constants. Obtain the equation of state, P as a function
of V and T, for this material.

Starting from the FE in the entropy representation (Eq. 4.8), we obtain the pres-
sure and temperature as:
1 S
aV bN 3
P S
aU bN 3
=
=
+

a
nd

=
=
+
T U V ,N N U 2V
T V U ,N N UV 2
!
!
(i)
Taking the ratio of the two expressions in (i),

Adapted from Problem 2.3-5 in Callen, H. B, Thermodynamics and Introduction to Thermo-
statistics, 2nd Ed., Wiley (1985).
83
aU bN 3
+ 2
P /T
= P = N UV 3
1/T
aV bN
+
N U 2V
!
aU 2V 2 + bN 4
U
NUV 2
=
=
U = PV
2 2
4
V
aU V + bN
NU 2V

(ii)
substituting (ii) into (i),
3
4
P aPV bN 3
b
=
+
= aPV + 3 P 2 V aV T = bT
3
T
N
PV
PV
!

bT
P=
V aV T
4.2 Manipulation of Thermodynamic Derivatives

Deriving relationships between thermodynamic derivatives is the key objective of
the present chapter. Manipulations of thermodynamic derivatives can seem quite
daunting at times, but can be accomplished systematically with a small number of
relatively simple mathematical tools. Thermodynamic functions, after all, are
mathematical objects that are subject to the same rules of multivariable calculus as
any other functions, even if we frequently do not have explicit, closed-form ex-
pressions for them in terms of their independent variables.
In the following, we will consider x, y, z, and w to be mathematical objects
with well-behaved functional relationships between them. We will also assume
that there are two independent variables in this set and that any two of x, y, z, and
w can serve as the independent variables. This assumption is made for simplicity
and without loss of generality. The following general mathematical relationships
are often useful for manipulating derivatives of functions of many variables in
general and thermodynamic functions in particular:
Inversion
x
1
=
y / x
y z
!
(4.9)
This relationship is for the underlying functions rather than simple algebraic in-
version; x(y,z) and y(x ,z) that are being differentiated on the two sides of Eq.
!
!
4.9 are expressed in terms of different variables (see Example 4.2 for an illustra-
tion of this concept).
84
Commutation
2z
z
z

=

(4.10)
=

x y
xy

x
y x y
x
y
!
In other words, mixed second derivatives are independent of the order in which
they are taken. This property applied to thermodynamic functions leads to equali-
ties between derivatives known as Maxwells relations.
Chain rule
(
(
)
)
x / w
x
x w
z
=
=

(4.11)
w y
y
y
/
w
z
z !!!inversion!
z
z
!!!!!!!!rule!!!
!
In Eq. 4.11 we have changed the independent variables from x(y,z) in the left-
!
hand-side to x(w,z) and y(w,z) in the right-hand-side.
!
!

Triple-product rule (also known as XYZ-1 rule)

This relationship links three cyclically permuted derivatives:
x y z

= 1
y z z x x y
!
(4.12)
Here, the three functions being differentiated, x(y,z) , y(x ,z) , and z(x ,y) ex-

!
!
!
press the same underlying relationship in terms of different variables. To prove
this equality, let us consider the differential form of the function x = x(y,z) :
x
x
dx =
dy +
dz
z y
y z
!
at constant x, this expression becomes:
x
x
dy x +
dz x = 0
z y
y z
!
Now let us obtain the derivative / z

!
of this relationship:

x y
x y
x
x
=0

+

=

z y
y z z x z y
y z z x
!
85
4.2 Manipulation of Thermodynamic Derivatives
x y z

= 1
y z z x x y
!
Example 4.2
Demonstrate how the inversion, commutation, chain and triple-product rules ap-
ply to the functions:
y2
x(y,z) =
; w = xz (variable transformation for the chain rule)
z
!
For the function x in the original representation, x = x(y,z) :
!

x / y = 2y /z
z
!
To test the inversion rule, we obtain the function in the representation
y = y(x ,z) :
!
y
y2
z
x=
y 2 = xz y = xz

=
z
x z
2 x
!
Now we need to eliminate x :

z
2 x
z
2 y 2 /z
z
1
=
2y x / y
y
1

=
(x / y)z
x z
!
For the commutation rule (independence on the order of differentiation), we have

2
2x 2y
2y
y
2 = 2
= =
z
yz z z y y z z

!
For the chain rule, the new variable is defined as w = xz . Then:
w
1
x / w =
z
z
z
2
y
w = xz =
z y = w y / w
z
!
x=
So that
( x / w )
( y / w )
!
1/z
1/2 w
2y
z
= x / y
1
2 w
86
For the triple-product rule we obtain:
x
x=
= 2y /z
z
y z
y2
y
y
x
y = xz
=
=
z x 2 z 2z
z=
!
y2
z
y2
z2
x
x y
x2
y2
x y z
2y y z 2
!
!
=
= 1
2
y
z
x
z
2z
y
z
x
One could have substituted variables other than y and z in the expressions for the
three cyclic derivatives with identical results.
4.3 Eulers Theorem for Homogeneous Functions

Thermodynamic functions and derivatives have special properties resulting from
the fact that they are either extensive (proportional to the size of the system) or
intensive (independent of the size of the system). Mathematically, functions that
satisfy the relationship
f (x) = f (x) for any x

!
are called homogeneous of degree one. Functions can be homogeneous of degree
one with respect to some, but not all the variables for example, a function that is
homogeneous of degree one with respect to variables x1,x2, ,xi and homogenous
of degree zero with respect to variables y1,y2, ,yj has the property:

f (x1 ,xi ,y1 ,y j ) = f (x1 ,xi ,y1 ,y j )!

!!for!any!!x1 ,xi ,y1 ,y j
(4.13)
!

Extensive thermodynamic functions are homogeneous of degree one with respect
to their extensive variables, and homogeneous of degree zero with respect to their
intensive variables.
Eulers theorem for homogeneous functions provides a link between such func-
tions and their derivatives, as follows:

!
f
f
f
f (x1 ,xi ,y1 ,y j ) = x1
+ x2
++ xi

x1
x2
xi
The proof of this theorem is as follows.
(4.14)
87
4.3 Eulers Theorem for Homogeneous Functions
f (x1 ,xi ,y1 ,)
!
=
f (x1 ,xi ,y1 ,)
f (x1 ,xi ,y1 ,) (x1 )

(x1 )
f (x1 ,xi ,y1 ,)
++
= f (x1 ,xi ,y1 ,)
f (x1 ,xi ,y1 ,) (xi )

(xi )
f (x1 ,xi ,y1 ,)
=
x1 + +
xi
x1
xi
!
Application of Eulers theorem to U (S ,V ,N1,N2, ,Nn), a homogeneous function of
degree one with respect to all its variables, gives:
U
U
U = S
+ V
+
S V ,{N }
V S ,{N }
!
Ni N
i=1
S ,V ,N

ji
U = TS PV + i Ni
i=1
!
(4.15)
This Euler-integrated form of the fundamental equation is sometimes confusing, as

it superficially appears to suggest that U is a function of twice as many variables as
previously (T and S, P and V, i and Ni). This is incorrect; despite appearances to
the contrary, the same variable set as before, ( S ,V ,N1,N2, ,Nn), is being used, with
temperature, pressure and chemical potentials that appear in the equation also
being functions of the same variables: T (S ,V ,N1,N2, ,Nn), P (S ,V ,N1,N2, ,Nn), and
i (S ,V ,N1,N2, ,Nn).
4.4 Legendre Transformations

Even though it is possible in principle to control the variables ( S ,V ,N ) experimen-
tally, it is much more common to perform experiments under constant-tempera-
ture or constant-pressure conditions, rather than at constant volume or entropy.
For example, constant-temperature conditions are closely approximated when a
system is immersed in a temperature-controlled bath. Constant-pressure condi-
tions are imposed when a system is open to the atmosphere. Variables such as T
and P appear as the first derivatives of the fundamental equation U (S ,V ,N ). Unfor-
tunately, while it is certainly possible to obtain functions such as U (T ,P ,N ), the
information content of such functions is not equivalent to that of the fundamental
equation U (S ,V ,N ) this is because of the integration constants that will need to
be introduced if one wants to go from U (T ,P ,N ) to U (S ,V ,N ), as illustrated in Ex-
ample 4.3.
Euler-
integrated
FE
88
In Chapter 2, we have already introduced an additional thermodynamic func-

tion, the enthalpy H = U + PV. Here, we will show that this and other similar de-
rived thermodynamic functions are more than just convenient combinations of
terms. They represent fundamental equations that play the same key role in ther-
modynamics as the energy U, but are expressed in variables other than ( S ,V ,N ).
In mathematical terms, for a function f(x ) of a single variable x, we would
like to obtain a new function g ( ), with the same information content as the origi-
nal function, but expressed in a new variable = df/ dx, the first derivative of the
original function. Equivalence of information content implies that the original
function can be recovered from the transformed one without any ambiguity in the
form of integration constants. It turns out that this can be done through a mathe-
matical operation known as a Legendre transformation. For a function of one vari-
able, the transformed function is obtained as g ( ) = f x , which has the following
properties:
d f = dx
dg = df xd dx = xd
!
(4.16)
In the new function (referred to as the transform of the original function), the
role of variables and derivatives has been exchanged: the derivative of the original
function is the variable of the new function and the variable of the original function
is minus the derivative of the transform. One can recover the original function by
simply applying the Legendre transformation one more time:
dg = xd
f = g + x
(4.17)
Example 4.3
Consider the function:
f (x) = x 2 + 2
Construct the function f(w ) and show that it cannot be used to fully determine

f(x ). Also obtain the Legendre transform of this function, g (w ) and show how it
can be used to reconstruct the original function f (x ).

The derivative of f (x ) is:

!
df
=
= 2x
dx
!
The function f( ) can be obtained by substituting x = / 2 in f (x ):
89
f () =
2
+ 2
4
(i)
Given f( ), we can attempt to determine f(x ) from:

2
df
dx 1
1
=
x = df =
= f 2 + c f = x c + 2
df
2 f 2
(ii)
An unknown integration constant c appears in expression (ii), so we have shown

that f(x ) cannot be fully recovered from f( ).
The Legendre transform g ( ) of f(x ) is:
2
g() = f x = + 2 g() = + 2
4
2
4
!
(iii)
From Eq. 4.17, the variable x can be obtained from (iii) from differentiation:
dg
x=
=
d 2
!
Now the function f(x ) can be obtained from g ( ) using Eq. 4.17 again:
f = g + x =
(iv)
2
+ 2+ w = + 2 f = x 2 + 2 QED
4
2
4
Example 4.4
Consider the function f ( x ) = x 3 + 1 in the interval [1,1]. Construct its first Legen-
dre transformation g ( ) and plot f (x ) and g ( ), marking the points correspond-
ing to x = 0.7, x = 0, and x = 0.7 on the graph of g ( ).

Using the definition of Legendre transforms:
df
= = 3x 2 x =

3
! dx
3/2

23/2
3/2
3/2
+1
g() = f x = +1
=
+1
g() =
3 3 3
3
3
3
3
!
!
The Legendre transform of g ( ) is:
dg
=
= x
3
! d
90
dg
23/2
3/2
=
+1
=
+1 = +1 = x 3 +1 = f (x)
g
d
3 3 3
3 3
3
!
Plots of the original and transformed functions are shown in Fig. 4.1. Arrows mark
the three points of interest (note that = 3x 2, so the coordinate corresponding to
x = 0.7 is = 30 .7 2 = 1.47.
The transform is multivalued two values of the function g () exist for any given
. This is the price we have to pay for ensuring that the reverse transform is
unique. In addition, the transformed function has a cusp at =0, with a discon-
tinuous first derivative. Multivalued functions arise naturally in thermodynamics
when a system can exist in multiple phases; cusps are also present in thermody-
namic functions for systems with multiple phases.

Figure 4 .1 A one-dimensional function and its transform.

For functions of many variables, the Legendre transform procedure can be applied
sequentially, giving the first, second and higher-order transforms. Formally, we
consider a general function of l variables, as a basis function y (0) , where basis
!
means simply the starting point of the transform:
y (0)(x1 ,x2 ,,xk ,xk+1 ,xl )

!
The first and second derivatives of the basis function are defined as:
(4.18)
91
i y (0)
i
y (0)
=
x i
!!!!and!!!!!!!!y (0)
ij
x j[i ]
(0)
2y (0)
y
!

=
=
(4.19)
x i x j
xi x j
xi[ j ]
x
j[i ]
Thus, the differential form of y (0) is:

!
dy (0) = 1x1 + 2x2 + + kxk + k+1xk+1 + lxl

(4.20)
!
The k-th transform of y (0) is denoted as y (k ) and is obtained from:
!
!
(k)
y (1 ,2 ,, k ,xk+1 ,xl ) = y (0) x11 x22 xk k (4.21)

!
The k-th transform is a function of a new set of variables, (1 ,2 ,, k ,xk+1 ,xl ) .
!
Its differential form is

dy (k) = x1d1 x2d2 xk d k + k+1dxk+1 + + l dxl (4.22)

!
A common basis function for thermodynamics is the fundamental equation in

the energy representation, U (S ,V ,N1,N2, ,Nn). Additional thermodynamic func-
tions, such as H, are simply transforms of the fundamental equation U that pre-
serve its information content. Note that different Legendre transforms result if the
order of variables of the original function is changed, for instance to
U (V ,S ,N1,N2, ,Nn).
Fundamental!equation:!!y (0) = U(S,V ,N1 ,N2 ,,Nn )

dU = TdS PdV + i dNi
(4.5)
i=1
The first Legendre transformation of U(S,V ,N1 ,N2 ,,Nn ) gives a new thermo-
!
dynamic function, the Helmholtz free energy A:

Fundamental!equation:!!y (1) = A(T ,V ,N1 ,N2 ,,Nn )
A = U TS ; dA = SdT PdV + i dNi
(4.23)
i=1
The second transform of U, gives another fundamental equation, the Gibbs free
energy G, named after American scientist Josiah Willard Gibbs (1839-1903):
Fundamental!equation:!!y (2) = G(T ,P,N1 ,N2 ,,Nn )
G = U TS + PV = A + PV ; dG = SdT +VdP + i dNi

i=1
!
(4.24)
92
Function
S V N
Internal energy U
!dA = SdT PdV + dN
V N
Helmholtz energy A
!dH = TdS +VdP + dN
S P N
Enthalpy H
!dG = SdT +VdP + dN
P N
Gibbs free energy G
Table 4.1 Fundamental equations (thermodynamic potential functions) for one-component systems.
Variables
!dU = TdS PdV + dN
!G = N
Differential
!H = TS + N
G
G
S=
V =
T P ,N
P T ,N
!
!
G
=
= G
N T ,P
!
H
H
T=
V =

S P ,N
P S ,N
!
!
H
=

N S ,P
V
T
=
S P ,N P S ,N
!
S
V
=

P T ,N T P ,N
2
2
NC P
S
T
T
H
G
=

=
= =
S 2 P ,N S P ,N NC P
T 2 P ,N T P ,N T
!
!
!A = PV + N
P
S

=
T V ,N
V T ,N
!
2
NCV
S
A

= =
T 2 V ,N T V ,N T
!
U
U
A
A
S =
T=
P=
P =

S V ,N
V S ,N
T V ,N
V T ,N
!
!
!
!
U
A

=
=

N S ,V
N T ,V
!
P
T
=

S V ,N V S ,N
2
T
T
U

= =
S 2 V ,N S V ,N NCV
!
!U = TS PV + N
Integral
First de-
rivatives
A second
derivative
Maxwells
rule
93
Reordering the variables to U(S,V ,N1 ,N2 ,,Nn ) gives the enthalpy H, first in-
!
troduced in deriving First Law balances for open systems as the first Legendre
(1)
transform y :
!
Fundamental!equation:!!y (1) = H(S ,P,N1 ,N2 ,,Nn )
H = U + PV ; dH = TdS +VdP + i dNi
(4.25)
i=1
The Legendre transforms of U are also known as thermodynamic potentials.

Table 4.1 (p. 92) summarizes the information on variables and derivatives for the
four thermodynamic potentials we have discussed thus far, for the case of a one-
component system for simplicity. The table also lists a second derivative for each
transform and an example Maxwells relationship between second derivatives.
The Euler-integrated form of each of the fundamental equations expresses
them as sum of terms, each term being an extensive variable of the transform mul-
tiplied by the corresponding derivative. The results are summarized in Table 4.1
and are consistent with the Legendre transformations above. For example, for the
Gibbs free energy G,
!G = N = U TS + PV = H TS = A + PV
(4.26)
An important consequence of the integral relationship for G in the special case of a

one-component system is that the molar Gibbs free energy is, in this case, equal to
the chemical potential:
for one-component systems only: !G =
(4.27)
Additional transformations, not listed in the table, are possible as well. For ex-
ample, one could order the variables as U(N1 ,N2 ,,Nn ,S,V ) and perform a single
!
transform to obtain a function of (1 ,N2 ,,Nn ,S,V ) . The resulting function is also
!
a valid fundamental equation, even if it is not frequently used in practice.
The final comment here is that the last transform, y (n+2) , yields a function of
!
only intensive variables, T, P and all the chemical potentials. By Euler integration
we obtain that the resulting function is identically zero, a result known as the
Gibbs-Duhem relationship:
n
SdT +VdP Ni d i = 0
i=1
!
(4.28)
Gibbs-
Duhem
relationship
4.5 Derivative Relationships

As already stated, two key objectives of classical thermodynamics are to obtain
relationships between properties, and to develop techniques to measure them. Ob-
taining thermodynamic relationships helps bring forward hidden connections
between seemingly unrelated quantities and facilitates the measurement and vali-
dation of physical property data.
The Legendre transformation facilitates developing relationships between
thermodynamic derivatives. For example, the following relationships exist be-
tween second derivatives of a transform and its basis function:
(1)
y11
=
!
y1i(1) =
y (1)
ij
!
y (0)
ij
y1i(0)
(0)
y11
1
(0)
y11
!!!!!i 1
(0) (0)
y1i
y1j
(0)
y11
!!!!!i, j 1
(4.29)
(4.30)
(4.31)
For proofs of these relationships, as well as more complex general relation-

ships between derivatives of the k-th transform and those of the basis function, see
Beegle, Modell and Reid, AIChE J., 20: 1194-200 (1974) and Kumar and Reid, AIChE
J., 32: 1224-6 (1986).
For pure components, a major simplification of thermodynamic relationships
is possible relative to the general multicomponent case, because composition is
not an independent variable. Extensive properties can then be normalized by the
amount of mass (moles) in a system to obtain intensive properties. Thermodynam-
ic derivatives at constant number of moles can be taken either on a total or on a
molar basis, for example:

U
(NU)
U
=
=
S
= T
V ,N (N S) NV ,N S V
!
(4.32)
N was eliminated in the last derivative of this expression because intensive prop-
erties do not depend on the size of the system, so that N is no longer a relevant
constraint. The differential forms of the fundamental equations in one-component
systems for the intensive thermodynamic functions U, A, G, and H, are as follows:
94
4.5 Derivatives in Terms of Measurable Properties
95
dU = TdS PdV
d A = SdT PdV

dH = TdS +VdP
!dG = SdT +VdP
(4.33)
First derivatives of these functions with respect to their natural variables are
obtained directly, either from Table 4.1 or from Eqs. 4.33. An example of such a
first derivative is given above in Eq. 4.32 temperature is clearly an experimental-
ly measurable quantity. Other examples include:
U
U
H
G
=
= P and
= = V
V
S ,N V S
P S P T
!
!
(4.34)
Some first derivatives of Fundamental Equations with respect to natural varia-

bles cannot be measured directly:
U
A
G
T = T = S and N =
S ,V
V P
!
!
(4.35)
First derivatives of Fundamental Equations with respect to unnatural varia-

bles or under other constraints can be obtained from the differential expressions
of Eq. 4.33. For example, to obtain the volume derivative of the energy at constant
temperature in terms of measurable properties, we start from:
!dU = TdS PdV
We now take the partial derivative ( / V )T , followed by Maxwells rule on A to

!
obtain:
U
S
P
V = T V P = T T P
T
T
V
!
(4.36)
Second derivatives of fundamental equations with respect to their natural var-

iables are important from a theoretical and experimental viewpoint. For example,
differentiating A and G twice with respect to temperature, we obtain two im-
portant experimentally measurable quantities, the heat capacities defined in Chap-
ter 3:
2 A
2 =
T V
!
C
S
1 U
= = V
T T V
T
T V
(4.37)
intensive
FEs for one-
component
systems
96
2 G
C
S
1 H
= P
2 = =
T T P
T
T P
T P
!
(4.38)
The other two second derivatives of G with respect to its natural variables are
also important experimentally measurable quantities. The cross derivative with
respect to temperature and pressure is:

!
V
2 G
G
=
=
= PV
TP
T P T
T P
P
(4.39)
This derivative is proportional to the coefficient of thermal expansion, defined as:
(V / T )P /V
! P
(4.40)
The second derivative with respect to pressure is:

2 G
V
2 =
= T V
P T P T
!
(4.41)
This derivative is proportional to the isothermal compressibility, which is defined

as:
(V / P)T /V
! T
(4.42)
Mixed second derivatives of fundamental equations with respect to their natu-

ral variables can be written in two equivalent ways, using the commutation prop-
erty (Maxwells relationships):
P
T
2U
= =

SV
S V
V S
(4.43)
P
S
2 A
=
=

T V
T V
V T
(4.44)
T
V
2H
=
=

S P
P S
S P
(4.45)
S
V
2G
= =
T P
P T
T P
(4.46)
!
It is clear from the last three expressions that derivatives of the entropy S with re-
spect to volume or pressure are experimentally measurable, even though the abso-
lute value of entropy itself is not directly obtainable in classical thermodynamics.
97
Other derivatives can be obtained using the tools described in 4.2. For exam-
ple, the Joule-Thompson coefficient, (T/P) H is the rate of temperature change
with pressure when a fluid flows across a throttling valve, as can be confirmed
from a differential First Law balance in an open system at steady state with d/Q =
d/W = 0 (see Eq. 2.18, p. 18). This coefficient can be expressed in terms of equation-
of-state derivatives and heat capacities by first invoking the triple-product rule:
(H / P)T
T H P
T
P T H = 1 P = (H / T )
H
P
T
H
P
!
The denominator is simply CP ; the numerator can be obtained from the differential
form of H,

H
S
V
dH = TdS +VdP
= T +V = T +V
P T
P T
T P
!
The final result is:
T
1 V
=
T
V

P
C P T P
H
(4.47)
Example 4.5 Differential expressions for U

Obtain differential expressions for U = U ( T ,V ) and U = U ( T ,P ) in terms of experi-
mentally measurable properties. Note that these expressions are not fundamental
equations because the natural variables of U are S and V.

We seek to construct expressions of the form:
U
U
dU = dT + dV
T V
V T
!
(i)
U
U
dU =
dT +
dP
T P
P T
!
(ii)
The temperature derivative (U /T) V = CV , and the volume derivative (U/V) T ,

have been obtained in Eq. 4.36, so the desired expression for U = U (T,V) is:
dU = CV dT + T P dV
T
V
!
(iii)
98
For the derivatives needed for expression (ii), we start again from the fundamental
equation for U in terms of its natural variables, dU = TdS PdV . Differentiating with
respect to T at constant P gives:
U
S
V
(iv)
T = T T P T
P
P
P
!
The temperature dependence of the entropy at constant pressure, (S / T) P , can
be obtained by differentiating dH = TdS + VdP:
H
S
T = C P = T T
P
P
!
After substituting the result into (iv), we get:
U
V
T = C P P T
P
P
!
The pressure derivative needed for (ii) is:
U
S
V
V
V
P = T P P P = T T P P
T
T
T
P
T
!
(v)
(vi)
We used Maxwells relationship on G to get rid of S. Substituting (v) and (vi) into
(ii) we finally obtain:
V
V
V
dU = C P P
+ P
dT T
dP
T P
P T
T P
!
(vii)
One observation we can make here is that the functional forms of U in unnatural
variables are more complex than the comparable expressions in its natural vari-
ables. This is an additional disadvantage beyond the loss of information content
discouraging the use of functional forms such as !U = U(T ,V ) and !U = U(T ,P) .
Example 4.6 Difference between heat capacities
Calculate the difference between the heat capacities at constant pressure and con-
stant volume, C P C V , for a general thermodynamic system, in terms of P, V, T and
their mutual derivatives.

We use as starting point expression (iii) in Example 4.5:
dU = CV dT + T P dV
T
V
!
99
Differentiating with respect to T at constant P and setting the result equal to ex-
pression (v) of Example 4.5, we obtain:
U
=
C
T
P !!!!!!from!(iii)!!! V
!
P
V
V
+ T P
=
C P P
T
T !!!from!(v)!!!
T P
V
P
P V
C P CV = T
T V T P
!

For ideal gases, one can simplify this relationship considerably:
(P / T )V = R /V !!!!and!!!!(V / T )P = R / P C P CV = TR2 /(PV ) = R

!
Thus, the difference in heat capacities at constant pressure and constant volume
for ideal gases is simply the ideal-gas constant R, as already derived in 2.4.

Chapter 5. Statistical Mechanical Ensembles

Boltzmanns microscopic expression for the entropy was introduced in 3.6:

S = kB ln(N ,V ,U)
!

(3.17)
where is the number of distinct microscopic states (microstates). The concept of

microstates arises naturally in quantum mechanics, but can be also introduced in
classical systems, if positions and velocities can be grouped so that, when their
values differ less than some selected (but arbitrary) small value, then they are con-
sidered to be equal. This quantization effect also arises naturally in computations,
which are performed with a finite numerical accuracy, so that two quantities can-
not differ by less than the machine precision.
Boltzmanns entropy formula links a macroscopic thermodynamic quantity,
the entropy, to microscopic attributes of a system at equilibrium. In this section,
we introduce many similar relationships for systems under constraints different
than (N,V,U), in a manner quite analogous to the introduction of fundamental equa-
tions in different variables developed in the previous chapter through the Legen-
dre transform formalism.
The branch of physical science that aims to connect macroscopic properties
and microscopic information about a system is called Statistical Mechanics. The
central question in Statistical Mechanics can be phrased as follows: If particles (at-
oms, molecules, electrons, nuclei, or even living cells) obey certain microscopic
laws with specified interparticle interactions, what are the observable properties
of a macroscopic system containing a large number of such particles? Unlike classi-
cal thermodynamics, statistical mechanics does require input information on the
microscopic constitution of mater of interest, as well as the interactions active
among the microscopic building blocks. The advantage of the approach is that
quantitative predictions of macroscopic properties can then be obtained, rather
than simply relationships linking different properties to each other. Another im-
portant difference between statistical mechanics and macroscopic thermodynam-
ics is that fluctuations, which are absent by definition in the thermodynamics, can
be quantified and analyzed though the tools of statistical mechanics. Fluctuations
are temporary deviations of quantities such as the pressure or energy of a system
from their mean values, and are important in small systems e.g. those studied by

Draft material from Statistical Thermodynamics 2012, A. Z. Panagiotopoulos
9/17/12 version

121

122
computer simulations, or present in modern nanoscale electronic devices and bio-

logical organelles.
5.1 Phase Space and Statistical Mechanical Ensembles

Postulate I states that macroscopic systems at equilibrium can be fully characterized
by n+2 independent thermodynamic variables. For a 1-component isolated system,
these variables can always be selected to be the total mass N, total volume V and
total energy U. However, at the microscopic level, molecules are in constant motion.
Adopting temporarily a classical (rather than quantum mechanical) point of view,
we can describe this motion through the instantaneous positions and velocities of
the molecules. Examples of microscopic and macroscopic variables are given below
for N molecules of a one-component monoatomic gas obeying classical mechanics.

Microscopic variables (in 3 dimensions)
Macroscopic variables
3N position coordinates (x, y, z)

3N velocity components (ux , uy , uz )
3 independent thermodynamic varia-

bles, e.g., N, V, and U.

Given that N is of the order of Avogadros number [NA = 6.02211023 mol1] for
macroscopic samples, there is a huge reduction in the number of variables re-
quired for a full description of a system when moving from the microscopic to the
macroscopic variables. Moreover, the microscopic variables are constantly chang-
ing with time, whereas for a system at equilibrium, all macroscopic thermodynam-
ic quantities are constant. The multidimensional space defined by the microscopic
variables of a system is called the phase space. This is somewhat confusing, given
that the word phase has a different meaning in classical thermodynamics the
term was introduced by J. Willard Gibbs, no stranger to the concept of macroscopic
phases.
In general, for a system with N molecules in 3 dimensions, phase space has 6N
independent variables
(r N ,pN ) (r1 ,r2 ,,rN ,p1 ,p2,pN )

(5.1)
!
where bold symbols indicate vectors, ri is the position and pi the momentum of the i-
the molecule, (pi = mi ui). The evolution of such a system in time is described by
Newton's equations of motion:

9/17/12 version
123
5.1 Phase Space and Statistical Mechanical Ensembles
dri
= ui
dt

du i
U(r1 ,r2 ,,rN )
mi
=
dt
ri
!
(5.2)
where U is the total potential energy, which includes interactions among molecules
and any external fields acting on the system.
For a much simpler system, a one-dimensional
harmonic oscillator shown in Fig. 5.1, phase
space is two-dimensional, with coordinates the
position and the momentum variables. In the
absence of friction, the oscillator undergoes
harmonic motion, which can be represented as
a circle in phase space if position and
momentum are scaled appropriately. The
diameter of the circle depends on the total
energy (a constant of the motion), and the
oscillator moves around the circle at a constant
velocity.

Figure 5.1 A one-dimensional har-
monic oscillator (top), and the cor-
responding phase space (bottom).
A statistical mechanical ensemble is a collection

of all microstates of a system, consistent with
the constraints with which we characterize a system macroscopically. For example,
a collection of all possible states of N molecules of gas in the container of volume V
with a given total energy U is a statistical mechanical ensemble. For the frictionless
one-dimensional harmonic oscillator, the ensemble of states of constant energy is
the circular trajectory in position and momentum space shown in Fig. 5.1 bottom.
5.2 Molecular Chaos and Ergodic Hypothesis

What causes the huge reduction from 3N time-
dependent coordinates needed to fully character-
ize a system at the molecular level to just a hand-
ful of time-independent thermodynamic variables
at the macroscopic level? The answer turns out to
be related to the chaotic behavior of systems with
many coupled degrees of freedom.
To illustrate this concept, one can perform a
thought experiment on the system shown in Fig.
5.2. In this system, a number of molecules of a gas
are given identical velocities along the horizontal
coordinate, and are placed in an insulated box

9/17/12 version

Figure 5.2 A conceptual exper-
iment in an isolated system.
124
with perfectly reflecting walls. Such a system would seem to violate the classical
thermodynamics postulate of eventually approaching an equilibrium state. Since
there is no initial momentum in the vertical direction, Newtons equations of mo-
tion would suggest that the molecules will never hit the top wall, which will thus
experience zero pressure at all times, even though there is a finite density of gas in
the system. In statistical mechanical terms, microstates with non-zero vertical
momenta will never be populated in such a system. Of course, even tiny interac-
tions between the molecules, or minor imperfections of the walls, will eventually
result in chaotic motion in all directions; thermodynamic equilibrium will be es-
tablished over times significantly greater than the interval between molecular col-
lisions.
Most molecular systems are able to forget their initial conditions and evolve
towards equilibrium states, by sampling all available phase space. Only non-
equilibrium (for example, glassy) systems violate this condition and have proper-
ties that depend on their history such systems cannot be analyzed with the
methods of equilibrium thermodynamics or statistical mechanics.
At a molecular level, the statement equivalent to Postulate I of classical ther-
modynamics is the ergodic hypothesis. The statement is as follows.
Ergodic
hypothesis
For sufficiently long times, systems evolve through all microscopic states con-
sistent with the external and internal constraints imposed on them.
Experimental measurements on any macroscopic system are performed by ob-
serving it for a finite period of time, during which the system samples a very large
number of possible microstates. The ergodic hypothesis suggests that for long
enough times, the entire ensemble of microstates consistent with the microscopic
constraints on the system will be sampled. A schematic illustration of trajectories
of ergodic and non-ergodic systems in phase space is shown in Fig. 5.3 a two-
dimensional representation of phase space is given, whereas we know that for re-
alistic systems phase space has a very large number of dimensions. The interior of
the shaded region is the phase space of the corresponding system. For the system

Figure 5.3 Schematic trajectories of ergodic (left) a nd non-ergodic (right) systems in
phase space.
9/17/12 version
125
5.2 Molecular Chaos and Ergodic Hypothesis
on the left, there are two connected regions of phase space, so the trajectory even-
tually passes from one to the other and samples the whole of phase space. By con-
trast, for the system on the right, the two regions of phase space are disconnected,
so that the system cannot pass from one to the other. The system is non-ergodic.
As already discussed in Chapter 1, there is a link between time scales and con-
straints; a system observed over a short time can appear to be isolated, while over
longer times it may exchange energy and mass with its surroundings. Also, the
possible microstates depend on the time scales of interest, and on internal con-
straints for example, chemical reactions open up additional microstates, but can
only occur over long time scales, or in the presence of a catalyst.
For systems satisfying the ergodic hypothesis, experimental measurements
(performed by time averages) and statistical mechanical ensemble averages are
equivalent. Of course, we have not specified anything up to this point about the rel-
ative probabilities of specific states; the ergodic hypothesis just states that all states
will eventually be observed. A general property F can be formally written as:

Fobserved
!
P
!!!!!probability!of!finding
the!system!in!microstate!
= < F >
value!of!property!F
!!!!!in!microstate!
ensemble
!!average
(5.3)
The objective of the next few sections will be to determine the relative
probabilities, P , of finding systems in given microstates of ensembles under vary-
ing constraints. This will allow the prediction of properties by performing ensem-
ble averages, denoted by the angle brackets of the rightmost side of Eq. 5.3.
5.3 Microcanonical Ensemble: Constant U, V, and N

The simplest set of macroscopic constraints that can be imposed on a system are
those corresponding to isolation in a rigid, insulated container of fixed volume V.
No energy can be exchanged through the boundaries of such a system, so Newtons
equations of motion ensure that the total energy U of the system is constant. For
historical reasons, conditions of constant energy, volume, and number of particles
(U, V, N) are defined as the microcanonical ensemble. In the present section (and
the one that follows), we will treat one-component systems for simplicity; general-
ization of the relationships to multicomponent systems is straightforward.
How can we obtain the probabilities of microstates in a system under constant
U, V, and N? Consider for a moment two microstates with the same total energy,
depicted schematically in Fig. 5.4. One may be tempted to say that the microstate
on the left, with all molecules having the same velocity and being at the same hori-
zontal position is a lot less random than the microstate on the right, and thus less
likely to occur. This is, however, a misconception akin to saying that the number
9/17/12 version
126
111111 is less likely to

occur, in a random se-
quence of 6-digit numbers,
than the number 845192.
In a random (uniformly dis-
tributed) sample, all num-
bers are equally likely to
occur, by definition. For mo-

Figure 5.4 Two microstates in an isolated system.
lecular systems, it is not
hard to argue that any spe-
cific set of positions and velocities of N particles in a volume V that has a given to-
tal energy, should be equally probable as any other specific set. There are, of
course, a lot more states that look like the right-hand side of Fig. 5.4 relative to
the left-hand side, the same way that there are a lot more 6-digit numbers with
non-identical digits than there are with all digits the same. The statement that all
microstates of a given energy are equally probable cannot be proved for the gen-
eral case of interacting systems. Thus, we adopt it as the basic Postulate of statisti-
cal mechanics:
Basic Postulate
of Statistical
Mechanics
For an isolated system at constant U, V, and N, all microscopic states of a system

are equally likely at thermodynamic equilibrium.
Just as was the case for the postulates of classical thermodynamics, the justification
for this statement is that predictions using the tools of statistical mechanics that rely
on this postulate are in excellent agreement with experimental observations for
many diverse systems, provided that the systems are ergodic.
As already suggested in 3.6, given that (U,V,N) is the number of microstates
with energy U, the probability of microstate in the microcanonical ensemble, ac-
cording to the postulate above, is:
1
P =

(U ,V ,N)
!
(5.4)
The function (U,V,N) is called the density of states, and is directly linked to the
entropy, via Botzmanns entropy formula, S = kB ln . It is also related to the fun-
!
damental equation in the entropy representation, with natural variables (U,V,N).
Writing the differential form of the fundamental equation for a one-component
system in terms of , we obtain:

!
dS
= d ln = dU + P dV dN
kB
9/17/12 version
(5.5)
127
In Eq. 5.5, we have introduced for the first time the shorthand notation
1/(kBT ) . This combination appears frequently in statistical mechanics, and is
!
usually called the inverse temperature, even though strictly speaking it has units
of inverse energy [J1]. Differentiation of Eq. 5.5 provides expressions for the in-
verse temperature, pressure, and chemical potential, in terms of derivatives of the
logarithm of the number of microstates with respect to appropriate variables:
ln
U
(5.6)
V ,N
ln
V = P
U ,N
!
(5.7)
ln
N =
U ,V
!
(5.8)
Example 5.1 A system with two states and negative temperatures

Consider a system of N distinguishable particles at fixed positions, each of which
can exist either in a ground state of energy 0, or in an excited state of energy . The
system is similar to that depicted in Fig. 3.13, except it has only 2 (rather than 3)
energy levels. Assuming that there are no interactions between particles, derive
expressions for the density of states and the temperature as a function of the ener-
gy, at the thermodynamic limit, N.

For a given total energy !U = M , the number of possible states is given by the ways
one can pick M objects out of N total particles:
N!

(U) = N =
M!(N M)!
M
!
At the limit of large N, we can use Stirlings approximation, !ln(N!) N lnN N :
ln (U) = N lnN N M lnM + M (N M)ln(N M)+ N M

N
!
ln (U) = N lnN M lnM (N M)ln(N M)

!
The temperature as a function of U is obtained from Eq. 5.6, taking into account
that the volume V is not a relevant variable for this system:
ln
=
=
U N
ln
(M )
N
9/17/12 version
128
1
1
=
( N ln N M ln M (N M )ln(N M )) = ( ln M 1+ ln(N M ) + 1)
M
N

= ln
kT
NM
N
= ln 1 B =
M
M
!
1

N
ln 1
M
The possible values of the normalized energy ratio, U /Umax = M / N , range from 0
!
(every particle is in the ground state) to 1 (every particle is in the excited state).
The relationship between M/N and the temperature is shown in Fig. 5.5. Low val-
ues of M/N correspond to low temperatures. Remarkably, the temperature ap-
proaches + as M/N from below, and then returns from negative infinity to
just below zero as M/N 1.

Figure 5.5 Temperature versus normalized energy for the system of Example Error!
Reference source not found..

Do these results make sense? Can negative temperatures exist in nature? It turns
out that the existence of negative temperatures is entirely consistent with thermo-
dynamics. The system of this example has a density of states that is a decreasing
function of the total energy U when more than half the particles are in the excited
state. Most physical systems (e.g. molecules free to translate in space) have a mon-
otonic increase in the number of states at higher energies, and thus cannot exist at
negative temperatures; however, some spin systems can closely approximate the
system of this example. One needs to realize that negative temperatures are effec-
tively higher than all positive temperatures, as energy will flow in the negative
positive direction on contact between two systems of opposite sides of the dashed
line M/N = , corresponding to = 0, or T = .
9/17/12 version
129
5.4 Canonical Ensemble: Constant N, V, and T

Just as in macroscopic thermodynamics, in statistical mechanics we are interested
in developing relationships for systems subject to constraints other than constant
U, V, and N. In Chapter 4, a change of variables was performed through the Legen-
dre transform formalism, which will turn out to be highly relevant here as well.
The first example to consider will be a system of fixed volume V and number of
particles N, in thermal contact with a much larger reservoir, as shown in Figure
5.6. Because energy can be transferred between the small system and the reservoir
without a significant change in the reservoirs properties, the small system is effec-
tively at constant temperature, that of the reservoir. The set of microstates com-
patible with constant-NVT conditions is called the canonical ensemble. Going from
the microcanonical (UVN) to the canonical (NVT) ensemble is akin to taking the
first Legendre transformation of the fundamental equation in the entropy represen-
tation. Note that the order of variables (UVN TVN) is important when performing
Legendre transformations; however, convention dictates that the canonical en-
semble is referred to as the NVT ensemble the ordering of variables is unim-
portant once a given transformation has been performed.
How do we derive the relative
probabilities of microstates for
the constant-temperature small
system? The total system (small
system + reservoir) is under con-
stant-UVN conditions. In the pre-
vious sections of this chapter, we
suggested that all microstates
of the total system, which is at
constant energy, volume and
number of particles, are equally
probable. However, a given mi-
crostate of the small system

with energy U is consistent with
Figure 5.6 A small system in contact with a large
many possible microstates of the
reservoir.

reservoir the only constraint is
that the energy of the reservoir is UR = U U . The number of such microstates for the
reservoir is

(U ) = R (U U )
! R R
The probability of finding the small system in state is proportional to the number
of such microstates,

9/17/12 version
130
P R (U U ) = exp ln R (U U )
!
(5.9)
We can Taylor-expand lnR around R (U) given that U is much smaller than U:
lnR
ln R (U U ) = ln R (U) U
+ !
(5.10)
U
!
Substituting 5.10 back in Eq. 5.9 and using Eq. 5.6, we can incorporate the term
involving Res (that does not depend on the microstate ) into the constant of
proportionality for P :

P exp U at constant N V T
!
(5.11)
This is a very important result. The probability of each microstate in the ca-
nonical ensemble (constant NVT) decreases exponentially for higher energies. The
probability distribution of Eq. 5.11 is known as the Boltzmann distribution.
In order to find the absolute probability of each microstate, we need to nor-
malize the probabilities so that their sum is 1. The normalization constant is called
the canonical partition function, Q and is obtained from a summation over all mi-
crostates,
canonical
partition
function
Q (N ,V ,T ) =
exp U
all!microstates!!
!
(5.12)
The probability of each microstate can now be written explicitly as an equality:
exp U
P =
at constant N V T
(5.13)
Q
!

The probability of all microstates with a given energy U is the a sum of (U ) equal
terms, each at the volume V and number of molecules N of the system:
(U)exp U
P(U) =
at constant N V T
(5.14)
Q
!

An important implication of these derivations is that the energy of a system at
constant temperature is strictly fixed. Instead it fluctuates as the system samples
different microstates. This is in direct contrast with the postulate of classical ther-
modynamics that three independent variables (N, V, and T in this case) fully char-
acterize the state of a system, including its energy. As will be analyzed in detail in
the following chapter, fluctuations of quantities such as the energy are present in
all finite systems, but their relative magnitude decreases with increasing system
size. For macroscopic systems fluctuations are negligible for all practical purposes,
except near critical points. In any statistical mechanical ensemble, however, we
9/17/12 version
131
need to make a clear distinction between quantities that are strictly constant (con-
strains, or independent variables in the language of Legendre transformations),
and those that fluctuate (derivatives).
Any thermodynamic property B can be obtained from a summation over mi-
crostates of the value of the property at a given microstate times the probability of
observing the microstate:

 = B P for any ensemble

(5.15)
all!microstates!
!
For example, the ensemble average energy ! in the canonical ensemble is
given by:
1
 = U exp U at constant N V T
(5.16)
Q !
!
Let us calculate the temperature derivative of the canonical partition function

Q . We have:

U exp U
lnQ
1 exp(U )
=
=
= 
(5.17)
The fundamental equation for S/kB , Eq. 5.5, has U, V and N as its variables and
, P , and as its derivatives. Its first Legendre transform with respect to U is:
S
S
U
U TS
U =
=
= A

(5.18)
kB
kB kBT
kBT
!
This is a function of , V , and N, with:
(A)
(5.19)
= U
V ,N

!
Comparing Eqs. 5.17 and 5.19, we see that the former (obtained from statisti-
cal mechanics) gives the ensemble average energy, recognizing that the energy
fluctuates under constant-NVT conditions. The latter expression, obtained from
thermodynamics using Legendre transformations, does not involve averages of
fluctuating quantities. At the thermodynamic limit, N , we can set the two ex-
pressions equal , and obtain a direct connection between the canonical partition
function and the first Legendre transform of S /kB ,

!A = lnQ
(5.20)
Eq. 5.20 relates a thermodynamic quantity, the Helmholtz energy A, to a micro-

scopic one, the partition function Q. This also allows us to confirm the Gibbs en-
9/17/12 version
132
tropy formula (Eq. 3.20, p. 59) for the case of a system at constant-N V T , in the
thermodynamic limit N :
= lnQ + U =
A +U S
=
kBT
kB
P lnP =
P lnQ U = lnQ P + PU =
Eq.!5.14
(5.21)
!
Given that lnQ is the first Legendre transformation of ln, we can now ex-
!
press all the first derivatives of the canonical partition function Q , analogous to
Eqs. 5.65.8 for the derivatives of the microcanonical partition function :
lnQ
= U
(5.22)

V ,N

!
lnQ

(5.23)
V = P
T ,N
!
lnQ

(5.24)
N =
T ,V
!
These expressions are strictly true only in the thermodynamic limit N; for
finite systems, for which we need to preserve the distinction between fluctuating
and strictly constant quantities, the proper expressions involve ensemble averag-
es; for example, the correct version of Eq. 5.22 is:

lnQ
= 

V ,N
!
(5.25)

Example 5.2 A system with two states in the NVT ensemble

Consider the system of N distinguishable particles at fixed positions, each of which
can exist either in a ground state of energy 0, or in an excited state of energy , in-
troduced in Example 5.1. Determine the mean energy as a function of temper-
ature in the canonical ensemble, and compare the result to the microcanonical en-
semble calculation of Example 5.1.

We denote the state of each particle i = 1,2, N by a variable li which can take the
values 0 or 1, denoting the ground or excited state. The total energy is
N
U = li
i=1
!
The partition function in the canonical ensemble is:

9/17/12 version
lnQ = ln e
Q =
133
N
N
exp
l
=
exp(li )
i
i=1 l1 ,l2 ,...,lN =0,1 i=1
l1 ,l2 ,...,lN =0,1
Now we can use a mathematical identity that will turn out to be useful in all cases
in which a partition function has contributions from many independent particles.
The sum contains 2N terms, each consisting of a product of N exponentials. We can
regroup the terms in a different way, in effect switching the order of the summa-
tion and multiplication:
!l1 ,l2 ,...,lN =0,1
exp(li ) = e
i=1
li
= (1+ e )N
i=1 li =0,1
You can easily confirm that the switched product contains the same 2N terms as
before. The final result for the partition function is:
!lnQ = N ln(1+ e )
The ensemble average energy is
lnQ
e
N

 =
=
N
=
() N ,V
1+ e 1+ e
!
The microcanonical ensemble result can be written as:
N
N
N

ln 1 =
= 1 = e M =
M = U =
M
M kBT
1+
e
1+
e
!
The only difference is that in the canonical ensemble the energy is a fluctuating
(rather than a fixed) quantity. Note also that the canonical ensemble derivation
does not entail any approximations; the same result is valid for any N. By contrast,
the microcanonical energy was obtained through the use of Stirlings approxima-
tion, valid as N. Small differences between the two ensembles are present for
finite N.
5.5 Generalized Ensembles and Legendre Transforms

The previous two sections illustrated how, starting from the fundamental equation
in the entropy representation and Boltzmanns entropy formula, one can obtain
relationships between macroscopic and microscopic quantities, first in the UVN
(microcanonical) ensemble, with key quantity the density of states, . A first Le-
gendre transformation of U to T resulted in the canonical ensemble, with partition
function Q. This process can be readily generalized to obtain relationships be-
tween microscopic and macroscopic quantities and partition functions for a sys-
tem under arbitrary constraints.
9/17/12 version
134
In our derivation, we start from the multicomponent version of the fundamen-

tal equation in the entropy representation,
n
dS
= d ln = dU + PdV i dNi
kB
i=1
(5.26)
We have already seen the first Legendre transformation:
S
y (1) = U = (TS U) = A
kB
!
(5.27)
The relationships between the original function and the first transform are de-
picted in the table below.

y(0) = S/kB = ln
y(1) = A/kBT = lnQ
Variable
Derivative
Variable
Derivative
1/(kBT) =
1/(kBT) =
P/(kBT) = P
P/(kBT) = P
Ni
i/(kBT) = i
Ni
i/(kBT) = i

These relationships link microscopic to macroscopic properties and are strictly
valid at the thermodynamic limit, N. One should keep in mind that in each en-
semble, the variables of the corresponding transform are strictly held constant,
defining the external constraints on a system, while the derivatives fluctuate they
take different values, in principle, for each microstate of the ensemble. The magni-
tude of fluctuations, and connections to thermodynamic derivatives, will be made
in Chapter 6.
Probabilities of microstates in two statistical ensembles have already been de-
rived. Microstate probabilities are all equal in the microcanonical ensemble, from
the basic postulate of statistical mechanics; they are equal to the Boltzmann factor,
exp(U), normalized by the partition function for the canonical ensemble (Eq.
5.13). Note that the factor U that appears in the exponential for microstate
probabilities in the canonical ensemble is exactly equal to the difference between
the basis function and its first Legendre transform, x11 .
!
One can continue this with Legendre transforms of higher order. The probabil-
ities of microstates in the corresponding ensembles can be derived in a way com-
pletely analogous to the derivation for the canonical ensemble, involving a subsys-

9/17/12 version
135
tem and bath of constant temperature, pressure, chemical potential, etc. In general,
the kth transform of the basis function is:
S
S
y (0) = !!!!!;!!!!!!!!!!y (k ) = 1x1 2x2 kxk
kB
kB
!
(5.28)
where i is the i-th derivative of y(0) with respect to variable xi . The probability
!
!
of a microstate in the ensemble corresponding to the kth transform is given by
P exp 1x1 2x2 kxk

(5.29)
!
where the variables xi and derivatives i refer to the original function y (0) . The
!
!
!
normalization factor (partition function) of the ensemble corresponding to the
transformed function, y (k ) is:
!
=

(5.30)
exp 1x1 2x2 kxk
all!microstates!
!
Using the partition function , the probability P can be written as an equality:

P =
!
exp 1x1 2x2 kxk
(5.31)
As was the case for the canonical ensemble, the partition function is simply re-
lated to the transformed function, y (k ) :
!
ln = y (k )
!
(5.32)
Example 5.3 Gibbs Entropy Formula

The Gibbs entropy formula,
S = kB P lnP
!
was derived in 3.6 for the microcanonical ensemble. Show that this relationship is
valid for all statistical ensembles.

We use the expression for the probability of microstates, P , in a generalized en-
semble, Eq. 5.31:
P lnP = P ln
exp 1x1 2x2 kxk
)=
P ( 1x1 2x2 kxk ln)
Now recall that the variables for the k-th transform are 1 ,2 ,, k ,xk+1 ,xn+2 ,
!
which are strictly constant in the corresponding ensemble, while the derivatives,
x ,x ,,xk , k+1 , n+2 fluctuate. We can rewrite the equation above taking this
! 1 2
into account:

9/17/12 version
136
P ( 1x1 2x2 kxk ln)
= 1 Px1 2 Px2 k Pxk ln =
= 1 < x1 > 2 < x2 > k < xk > ln
From Eqs. 5.28 and 5.32,
S
ln = y (k ) = 1x1 2x2 kxk
kB
!
At the thermodynamic limit, N, so there is no distinction between ensemble
averages and thermodynamic properties, < xi > xi . Replacing !ln and simplify-
!
ing,
P lnP = k
, QED

Example 5.4 Grand Canonical (VT) (NPT) Ensemble
The grand canonical (constantVT) and constant-pressure (NPT) ensembles are
frequently used in computer simulations. Derive the partition functions, probabil-
ity of microstates, and derivative relationships in these two ensembles for a 1-
component system.

Starting from the fundamental equation in the entropy representation with order-
ing of variables y (0) = S(U ,N ,V )/kB = ln , the grand canonical ensemble partition
!
function corresponds to:
S
TS U + N

ln = y (2) = U + N =
kB
kBT
!
The microstates possible in this ensemble include all possible particle numbers
from 0 to , and all possible energy levels.
The Euler-integrated form of the fundamental equation is !U = TS PV + N , so that
the partition function of the grand canonical ensemble can be linked to the follow-
ing thermodynamic property combination:
PV
ln =
= PV
kBT
!

9/17/12 version
137
y (2) = PV = ln
!
y (0) = S /kB = ln
!
Variable
Derivative
Variable
Derivative
U
N
V
U
N
P

For example, the average number of molecules in the system is given by:
ln
ln
= < N >
() = < N > kBT
,V
,V
!
The probability of microstates in this ensemble is:
P =
!
exp(U + N )
, where = exp(U + N )

Example 5.5 Constant-pressure (NPT) Ensemble
The constant-pressure (NPT) ensemble is also frequently used in computer simu-
lations. Derive the partition functions, probability of microstates, and derivative
relationships in this ensembles for a 1-component system.

Ee start from from the fundamental equation in the entropy representation with
ordering of variables y (0) = S(U ,V ,N)/kB , and obtain the second transform:
!
S
TS U PV
ln = y (2) = U PV =
= N = G
kB
kBT
!
The microstates possible in this ensemble include all possible volumes from 0 to
, and all possible energy levels.
The derivative table is:

y (2) = N = ln
!
y (0) = S /kB = ln
!
Variable
Derivative
Variable
Derivative
U
V
N

P
N
U
V

9/17/12 version
138
For example, the average volume is given by:
ln
ln
= < V >
(P) = < V > kBT P
,N
,N
!
The probability of microstates in this ensemble is:
P =
!
exp(U PV )
, where = exp(U PV )
9/17/12 version
Chapter 6.
Equilibrium, Stability, and Fluctuations
The First and Second Laws of Thermodynamics allow us to make powerful general
statements about the overall behavior of systems in thermodynamic equilibrium
with respect to external interactions in particular, we have learned how to obtain
work and heat flows and entropy changes of a system and its environment. We
have also established that irreversible (spontaneous) changes within a system re-
sult in a net increase in the entropy of the universe. We have not yet examined,
however, the detailed internal requirements and constraints imposed by thermo-
dynamic equilibrium on properties and thermodynamic functions of systems. Ex-
perience suggests that for a system at equilibrium, density does not need to be uni-
form; for example, a vessel containing a liquid and its saturated vapor clearly has
density variations. However, temperature is uniform throughout systems at equi-
librium, at least at the level of macroscopic measurements. This must somehow be
connected to the overall condition imposed by the Second Law that the entropy of
the universe is maximized at equilibrium, but the link has not yet been made ex-
plicit.
A key difference between macroscopic thermodynamic and statistical
mechanical points of view is that the latter recognizes the existence of fluctuations
occuring in small regions of a system at equilibrium. Such fluctuations are
completely absent in macroscopic thermodynamics. We have alluded in the
previous chapter that the two seemingly contradictory statements are reconciled
at the limit N. In the present chapter, we will develop the necessary framework
for performing this reconciliation. Interestingly, the existence of microscopic
fluctuations will turn out to be intimately linked to thermodynamic stability:
macroscopic systems become unstable when their microscopic fluctuations
become unbounded.
The goals of the present chapter are to examine the conditions of equilibrium
and stability of thermodynamic systems, and to obtain relationships expressing
microscopic fluctuations in terms of system properties. We also obtain constraints
on the signs and relative magnitudes of thermodynamic derivatives that follow
from the equilibrium and stability conditions. In Chapter 5, we studied methods to

Draft material from Statistical Thermodynamics 2012, A. Z. Panagiotopoulos
10/4/12 version
152
153
6.1 Equilibrium Criteria
manipulate derivatives of fundamental equations and to obtain relationships

among them. Some of these derivatives, e.g. the thermal expansion coefficient P ,
can be positive for some systems and negative for others. A well-known example
of negative thermal expansion coefficient is liquid water between 0 and 4 C. With-
in this temperature range, water contracts upon heating, while most other sub-
stances (as well as water outside this range) expand on heating. Does thermody-
namics place any restrictions on derivatives such as the isothermal compressibility
or heat capacities CV and CP? These and similar questions are addressed in the
sections that follow. Conditions of equilibrium also allow us to establish general
constraints on how many phases can coexist at equilibrium (Gibbs phase rule).

One of the consequences of the Second Law of Thermodynamics is that entropy is
maximized for isolated closed systems at equilibrium (see 3.4). Isolated systems
can be considered to be at constant (U ,V ,N ), since they do not exchange heat,
work or mass with their environment. One example of an isolated system is the
universe itself. Irreversible (spontaneous) processes bring systems from off-
equilibrium states to equilibrium states. We have shown (Eq. 3.10, p. 45) that the
entropy of an isolated closed system increases when the system undergoes an ir-
reversible process leading to an equilibrium state. Therefore,

S is maximized at equilibrium when ( U ,V ,N ) are constant
This condition turns out to be a good starting point for deriving equilibrium
criteria for systems subject to different constraints. Let us consider a small pertur-
bation within an isolated system containing a pure component, as shown in Fig.
6.1. This perturbation could be a change in energy, volume or amount of material
in a region that is labeled system I, while the rest of the isolated system is labeled
system II. The first-order variation in the overall entropy is:
S = SI + SII
(6.1)
!

Using the fundamental equation in the entropy representation for a one-compo-
nent system (p. 82):
P
1
SI = UI + I VI I NI
TI
TI
TI

(6.2)
PII
II
1
SII = UII + VII NII
TII
TII
TII
!
10/4/12 version
154
Chapter 6. Equilibrium, Stability, and Fluctuations
Since the overall system is isolated, its energy, volume, and number of moles
are fixed; variations within the two subsystems must be linked so as to satisfy:
UI + UII = 0 UI = UII
VI + VII = 0! VI = VII
(6.3)
N + NII = 0 NI = NII
! I
Substituting the expressions from Eqs. 6.2 and 6.3 into Eq. 6.1, we obtain:

1 1
P P

S = UI + I II VI I II NI
TI TII
TI TII
TI TII
!
(6.4)
The variations UI , VI , and NI are independent of each other: we can certain-

ly envision a fluctuation in the volume of a subsystem that leaves its energy and
number of moles unchanged. The fact that the entropy of the overall isolated sys-
tem is a maximum at equilibrium implies that all the prefactors of the independent
variations in Eq. 6.4 must be zero:

!
equilibrium
criteria,
1-component
systems

P P
I II
1 1
= 0!!!; I II = 0!!!;
= 0
TI TII
TI TII
TI TII
TI = TII

PI = PII
(6.5)
= II
! I
In words, maximization of the entropy implies that temperature, pressure and
chemical potential must be uniform at equilibrium. Even though we derived this
Figure 6.1 A subsystem within an isolated system.
10/4/12 version
155
result for the case of an isolated system at

constant (U ,V ,N ), it applies to all sys-
tems at equilibrium, irrespective of the
constraints placed upon them. This is be-
cause setting a different constraint, e.g.,
constant (T ,V ,N ), imposes uniformity of
temperature throughout the total system,
so the first condition of Eq. 6.5 is auto-
matically satisfied. Generalization to n-
component systems is straightforward,
resulting in the condition that the chemi-
cal potential for each component must be
uniform in multicomponent systems at
equilibrium, in addition to the tem-
perature and pressure equality condi-
tions:

Figure 6.2 Variation of entropy for a
system at constant U.
TI = TII

PI = PII
(6.6)
= i ,II !!for!i = 1,2,...n

! i ,I
Entropy is the fundamental equation with natural variables (U,V,N). The fact
that it is a maximum for an isolated system when variables (U,V,N) are held con-
stant suggests the hypothesis that other fundamental equations also reach an ex-
tremum under the constraint that their own natural variables are held fixed. To
show this, we first turn our attention to the energy U, which has natural variables
(S ,V ,N ). As we will immediately show, maximization of entropy S at constant
(U ,V ,N ) implies minimization of the energy U at constant ( S ,V ,N ).
Consider Fig. 6.2, showing schematically the variation of entropy as a system
moves slightly away from equilibrium point A at constant (U ,V ,N ). Since entropy
is a maximum at equilibrium, the off-equilibrium state of the system (point B, with
UB = UA) will have entropy lower than that of the equilibrium state A. Now, we
would like to consider a similar small excursion away from the original equilibri-
um state A of the system, but this time at constant S. We can bring the system from
point B to point C, which has the same value of the entropy as the initial state A, by
supplying a small amount of heat, Q, in a reversible fashion, so that Q = TS. Since
S = SA SB = SC SB > 0 because the entropy is a maximum at equilibrium, the amount

of heat is also positive, Q > 0; heat must be supplied to the system. We perform a
First Law balance taking into account that work is zero because of the constant-
volume condition:
10/4/12 version
equilibrium
criteria,
n-component
systems

156

Figure 6.3 System in contact with a thermal reservoir

U = UC UB = UC U A = Q +
> 0
V !is!constant
!
The small change from an equilibrium to an off-equilibrium state resulted in
U > 0 at constant entropy: the energy increases when we move away from equilib-
rium at constant ( S ,V ,N ). Therefore, we have shown that:
U is minimized at equilibrium when ( S ,V ,N ) are constant
The next step is to examine the behavior of systems that are subject to con-
straints different from (U ,V ,N ) or (S ,V ,N ). The derivations parallel the develop-
ment of alternate representations of the fundamental equation in Chapter 5, in
which we moved from the energy U (S ,V ,N ) to the Helmholtz energy A (T ,V ,N ) or
Gibbs free energy G (T ,P ,N ). First, let us consider the constant-(T ,V ,N ) case by
analyzing a small system in contact with a large thermal reservoir as shown in Fig.
6.3. Changes in energy of the small system result in negligible changes in the prop-
erties of the large reservoir, which imposes its temperature on the small system.
Water baths used in chemistry and biology labs are good examples of (approxi-
mately) constant-temperature reservoirs. We will consider the sum of (system +
reservoir) to constitute a total system that is isolated (constant U ,V ,N ), so that:

Stotal = S + SR
10/4/12 version
(6.7)
157
We have used the subscripts total and R to distinguish properties of the total sys-
tem and the reservoir, respectively. The system of interest (the one being held at
constant T, V and N), is assigned no special label. For the total system, the entropy
is a maximum at equilibrium as the system is at constant ( U ,V ,N ). For any process
that takes the system from an off-equilibrium to an equilibrium state, we must
have Stotal > 0 . For the total system, we have:
U
= 0 U + UR = U +TSR
! total
(6.8)
Here, we have assumed that the transfer of heat from the system to the reservoir
takes place reversibly, since both system and reservoir are at the same tempera-
ture. Furthermore, there is no volume change or work associated with the reser-
voir, so UR = TSR. Now, from Eq. 6.7, we have:
S = Stotal S
! R

Eq. 6.8 now gives:

U
= 0 = U TS +TStotal U TS = TStotal < 0
! total
Since the system is at constant T,

!U TS = (U TS) = A < 0
We have thus shown that moving towards equilibrium results in lowering of the
Helmholtz free energy A, so that:

A is minimized at equilibrium when ( T ,V ,N ) are constant
The energy U is not minimized at equilibrium at constant (T ,V ,N ), except at

very low absolute temperatures, for which the Helmholtz energy A = U TS becomes
identical to U. One manifestation of this fact is that solids melt above a specific
temperature, even though the lowest energy arrangement of molecules of most
substances corresponds to a crystalline solid. The resulting liquids have higher
energy U than their crystals, but also higher entropy S. The Helmholtz energy A is
lower for the liquids above the melting point, making them the stable thermody-
namic states. In other words, liquids exist because A is minimized rather than U at
constant temperature. Another example is the spontaneous folding of many pro-
teins in solution into specific three-dimensional patterns encoded in their amino
acid sequences. Even though energy minimization is often used to search for stable
folded states, the correct thermodynamic function to be minimized is A, not U.
However, calculation of A is much harder than calculation of U, so minimization of
A is often not done because it is computationally impractical.
10/4/12 version
158
Let us now consider closed systems at constant T, P and N. A schematic dia-

gram of such a system is shown in Fig. 6.4. The small system of interest is connect-
ed on the left side to a large thermal reservoir by a diathermal rigid wall and on
the right side to a large volume reservoir by a movable, insulated piston. The
thermal reservoir imposes its temperature, and the volume reservoir imposes its
pressure on the system of interest, since variations in the systems energy or vol-
ume are too small to affect the properties of the reservoirs. Once more, we will
consider the sum of (system + thermal reservoir + volume reservoir) to constitute
a total system that is isolated (constant U ,V ,N ), so that its entropy is maximized
at equilibrium:
S
= S + ST'res + SP'res > 0
! total

(6.9)
The entropy change of the volume reservoir is zero because there is no heat flow
into or out of it. The total energy Utot is constant, so that:
U total = 0 = U + UT(res + UP(res = U +TST(res P VP(res
VP(res =V
U
= 0 = U +TST(res + PV TST(res = U PV
! total
Substituting in Eq. 6.9:

TStotal = TS +TST'res = TS U PV = (U TS + PV ) = G > 0

!
G < 0
Figure 6.4 System in contact with thermal and volume reservoirs
10/4/12 version
159
So that:

G is minimized at equilibrium when ( T ,P ,N ) are constant
In a similar fashion, one can prove that for any set of constraints on a system,
the thermodynamic function that corresponds to a fundamental equation with the
corresponding variables is minimized or maximized at equilibrium, depending on
whether we start from the fundamental equation in the energy or entropy repre-
sentations.
A connection to the statistical mechanical ensembles introduced in the previ-
ous chapter can also be made. We have seen that a given set of external constraints
imposed on a system define a statistical ensemble, with partition function equal to
the exponential of the corresponding Legendre transformation. The starting point
is y (0) = S /kB , which corresponds to constantUVN conditions. The condition of
!
equilibrium for a system at constantUVN, is, as we have just established, the max-
imization of the entropy S, and therefore also of y (0) . The first Legendre transform
!
corresponds to a system at constantNVT conditions:
S
U
U TS
lnQ = y (1) =
=
= A
kB kBT
kBT
!
We have just established that the Helmholtz free energy A is minimized at con-
stantNVT conditions, so that A is maximized. Thus, we can generalize this ob-
servation as follows.
At the set of conditions that define a statistical mechanical ensemble, the thermo-
dynamic function corresponding to the partition function of the ensemble is max-
imized at equilibrium.
Example 6.1
Determine the thermodynamic potential functions being minimized or maximized
at equilibrium:
(a) at constant ( S ,P ,N )
(b) at constant ( T ,V , )

(c) at constant (1/T ,P/T ,N)
For (a), we can see directly that the thermodynamic function being minimized is
the fundamental equation in the variables ( S ,P ,N ):
H (S, P, N) = U + PV is minimized at equilibrium for constant (S, P, N)
10/4/12 version
160
For (b), the function being minimized is a Legendre transform of U that we have
not formally defined, but should be a function of (T, V, ). To obtain this function,
we need to transform T and N in U (S, V, N), so that the function is
= UTS = PV
We conclude that the function = PV is minimized at equilibrium for constant (T,
V, ), given that the starting point was U, so that P V is maximized.
For (c), the variables are related to the entropy representation of the fundamental
equation,
1
P
dS = dU + dV dN
T
T
T
!
To obtain a function of (1/T ,P/T ,N), we need to transform the first two variables
to obtain the function:
S U/T PV/T = ( U TS +PV )/T = G/T,
which is maximized at equilibrium, as the starting point was S.

More complex types of equilibria can
be encountered in systems with internal
boundaries. A noteworthy example of
such boundaries is semipermeable mem-
branes that do not allow exchange of
molecules of certain components be-
tween the two sides of the membrane. A
schematic of such a system is shown in
Fig. 6.5. The overall system is considered
under conditions of isolation, at constant
U, V, and N. At equilibrium, the entropy of
the total system is maximized:

Figure 6.5 System with a rigid membrane
permeable only to component A.
S = SI + SII
! tot
(6.10)
Since the membrane is rigid, the volumes of the two compartments are constant;
the number of moles of component B is also constant on both sides; however, the
energies can fluctuate because of molecules of component A moving across the
membrane. The variations of entropy are:
SI =

A ,I
1
UI
N A ,I
TI
TI
A ,II
1
SII = UII
N A ,II
TII
TII
!
10/4/12 version
(6.11)
161
The conditions of isolation of the total system impose conservation of energy and
number of moles of A in the two regions

UI + UII = 0 UI = UII
N + N A ,II = 0 N A ,I = N A ,II
! A ,I
(6.12)
Substituting in the expression for Stot above,

!

A ,I A ,II
1 1
Stot = UI
N
TI
TII A ,I
TI TII
!
At equilibrium, the first-order entropy variation must vanish for all possible per-
turbations, so that the prefactors to UI and N A ,I must both be zero. The condi-
!
!
tions of equilibrium are then:
TI = TII
= A ,II
! A ,I
(6.13)
6.2 Stability Criteria

We have just established in 6.1 that equilibrium in thermodynamic systems un-
der a certain set of external constraints implies that a thermodynamic potential
(fundamental equation) is minimized or maximized. There are, however, addition-
al mathematical requirements for minimization or maximization of functions. For
a simple one-dimensional mechanical system of a ball in a gravitational well (Fig.
6.6), the energy function U is at a minimum with respect to position x when:

dU
= 0 [condition of extremum]
! dx
(6.14)
Eq. 6.14 is a necessary but not sufficient condition for minimization of U. In par-
Figure 6.6 Types of mechanical equilibrium in a one-dimensional system.
10/4/12 version
162
ticular, the following additional condition must be satisfied by the second deriva-
tive of U at the point at which the first derivative vanishes to make it a minimum:

d 2U
! dx
> 0 [minimization condition]
(6.15)
The left-most panel of Fig. 6.6 satisfies the condition of Eq. 6.15 and corre-
sponds to a stable equilibrium state. Small perturbations of the system to either left
or right of the minimum produce a restoring force that returns the system to the
stable equilibrium point. For the second panel from the left, the second derivative
is negative and the point corresponds to a maximum. Such a condition corre-
sponds to unstable equilibrium. At exactly the top of the hill the forces on the ball
are zero, so in principle the ball is at equilibrium. However, the slightest perturba-
tion away from this point to either left or right results in forces that move the ball
away from the point of equilibrium; systems cannot be kept for any significant
amount of time at unstable equilibrium, but move away towards stable equilibri-
um states.
An additional possibility for a type of equilibrium state is illustrated in the
third panel of Fig. 6.6. The well in this case has two minima, a shallow one to the
left and a deeper one to the right. There is no simple mathematical test to distin-
guish between a global minimum and a local minimum: in both cases, the first de-
rivative vanishes and the second derivative of the function at the minimum is posi-
tive. Systems that are at a local minimum of the appropriate thermodynamic po-
tential are said to be in metastable equilibrium. Small perturbations away from a
metastable equilibrium state return to the starting point, but large perturbations
can lead to a drastically different equilibrium point. As the depth of the metastable
well is reduced, we reach a limit of stability (right-most panel of Fig. 6.6), for
which:

dU
d 2U
= 0!!!and!!!
= 0 [limit of stability]
dx 2
! dx
(6.16)
Real thermodynamic systems are frequently found in metastable states. A liq-

uid being heated in a clean glass container may exceed its boiling point in the ab-
sence of nucleation sites. Rapid boiling will occur when a nucleation event takes
place in such a superheated liquid, with possible risks to nearby people and equip-
ment. This is the reason boiling stones providing nucleation sites are always
used in chemistry laboratories when heating liquids. In a similar way, a liquid may
cool below its melting temperature without nucleation of the solid, becoming a
supercooled liquid, but provision of a suitable nucleus in such a system results in
rapid crystallization. Jet aircraft often leave behind contrails because their ex-
haust gases provide nucleation sites for supersaturated water vapor in the atmos-
phere.
10/4/12 version
163
One may well question the applicability of thermodynamics to such metasta-

ble states. After all, we have established in Chapter 1 that thermodynamics applies
only to stable equilibrium states, fully characterized by n+2 independent thermo-
dynamic variables. Metastable states are not, strictly speaking, at equilibrium.
However, if they are sufficiently long-lived, they are indistinguishable from stable
equilibrium states and their thermodynamic properties are well defined. Recalling
the discussion in 1.3 of time scales involved in deciding if a boundary is permea-
ble. There are similar considerations of time scales with respect to metastable
states. If the time scales of interest are much shorter than the metastability barrier
crossing times, metastable states can be properly described by equilibrium ther-
modynamics.
Up to this point, the conditions of equilibrium and stability, Eqs. 6.14 to 6.16,
have been written for one-dimensional functions. Thermodynamic potentials are
functions of n+2 variables, so the conditions of maximization or minimization are
more complex. Mathematically, the condition of stability for functions of many var-
iables is expressed as a condition on the sign of its second-order variation. For ex-
ample, in the case of a system at constant ( S ,V ,N ) the energy is minimized at equi-
librium, so for the first-order variation we have U = 0. For the second-order varia-
tion we must have:
2U > 0
2 U
(S)2 +
2
2 U
(V )2 +
2
2 U
2
(N)2 +
S
V
N

2
2
U
U
2 U
!!!!!!!!!!!!!!!!!!!!!!!! + 2
SV +
SN +
VN > 0
S N
V N
S V
Since the variables S, V, and N are independent, we can consider variations in

which only one of the S, V or N terms are non-zero. In those cases, only one of
the first three terms will contribute to 2U. To ensure that 2U > 0 in this case, a
necessary but not sufficient condition is that the corresponding coefficients must
be positive:

2U
T
T
T
>0
=
>0
> 0
2
CV
S V ,N NCV
S V ,N
!
(6.17)
2U
P
P
< 0 < 0
2 >0
V S ,N
V S
V S ,N
!
(6.18)
2U

2 >0
> 0
N S ,V
N S ,V
!
(6.19)
10/4/12 version
164
Eq. 6.17 is known as the condition of thermal stability and suggests that the
constant-volume heat capacity of any stable thermodynamic system must be posi-
tive. Even though we derived this expression for a one-component system at con-
stant ( S ,V ,N ), this is a general relationship valid also for multicomponent systems
under arbitrary constraints. Note also that at constant N, we can move from exten-
sive to intensive variables in expressing the final form of the stability criteria.
We have already suggested that these are necessary but not sufficient conditions
of stability for thermodynamic systems. In order to obtain necessary and sufficient
conditions, we need to convert !2U to a quadratic form. We can do this as follows.
We start from U = y (0) as the basis function. The second-order variation of U can be
!
written as:

2U = 2y (0) =
!
n+2 n+2
yij(0) xix j
(6.20)
i=1 j=1
Now we define auxiliary variables, zk as follows:

!

zk = xk +
n+2
ykj(k )x j !!!!for!k = 1,2,,n +1
j=k+1
(6.21)
z
= xn+2
! n+2
It can then be shown using the properties of Legendre transformations that:

2U = 2y (0) =
!
n+1
ykk(k1) zk2
(6.22)
k=1
In other words, the use of the auxiliary variables zk reduces the fundamental equa-
!
tion for U to a quadratic form. We demonstrate in the example below how this ap-
proach works for a function of two variables, equivalent to the intensive form of U
in a one-component system.
Example 6.2 Demonstration of Eq. 6.22
Demonstrate Eq. 6.22 for a function of two variables, y (0) = f (x1 ,x2 ) .

!
The second-order variation of f is:
(0) 2
(0)
(0) 2
2f = 2y (0) = y11
x1 + 2y12
x1x2 + y22
x2
!

The auxiliary variables of Eq. 6.21 are, in this case:
(1)
z = x1 + y12
x2
! 1

Beegle, B. L., Modell M., and Reid, R. C., AIChE J. 20:1200-6 (1974).
10/4/12 version
165
z = x2

! 2
Eq. 6.22 can be written explicitly as:
2
ykk(k1) zk2
!k=1
(0)
(1)
(0)
(1)
(1)
= y11
z12 + y22
z22 = y11
x1 + y12
x2 + y22
x22
(i)
We now show that this expression can be reduced to Eq. 6.20, using the step-
down relationships of 4.5:
(1)
y11
=
1
(0)
y11
(1)
!!!;!!!!y12
=
(0)
y12
(0)
y11
(1)
(0)
!!!;!!!!y22
= y22
( )!
(0)
y12
(0)
y11
Substituting in (i) above,
( )
2
2
(0)
(0)

y12
y
ykk(k1) zk2 = y11(0) x1 + y12(0) x2 + y22(0) y(0) x22 =

k=1

11
11
(y ) x
x +
(0)
(0)
= y11
x12 + 2y12
(0)
12
(0)
y11
2
2
2
(0)
+y22
x22
(y ) x
(0)
12
(0)
y11
2
2
(0)
(0)
(0)
= y11
x12 + 2y12
x2 +y22
x22 = yij(0) xi x j !!!!!!!!!QED
i=1 j=1
Given that Eq. 6.20 is a quadratic form, we can now state that the necessary and
sufficient conditions for stability in a general n-component system are that the fol-
lowing n+1 second derivatives of the basis function and its Legendre transforms
are positive:

y (k1) > 0!!!for!k = 1,2,n +1

! kk
(6.23)
Reordering the variables of the basis function leads to a different (but equiva-
lent) set of stability conditions. For example, for a one-component system, the fol-
lowing is a non-exhaustive list of equivalent sets of stability conditions:

P
T
(0) T
(1)
y (0) = U(S,V ,N) y11
=
=
> 0!!!;!!!y22
= > 0 (6.24)
S V ,N NCV
V T ,N
10/4/12 version
166
T
(0) T
(1)
y (0) = U(S,N ,V ) y11
=
=
> 0!!!;!!!y22
=
>
0
(6.25)
S N ,V NCV
N T ,V
P
T
(0)
(1) T
y (0) = U(V ,S,N) y11
= > 0!!!;!!!y22
= =
> 0 (6.26)
V S ,N
S P ,N NC P
(0)
(1) T
y (0) = U(N ,S,V ) y11
=
>
0!!!;!!!y
=
>
0

S
22
N S ,V
,V
(6.27)
Thus, thermodynamic stability requires that all the second derivatives of funda-
mental equations with respect to a single one of their extensive natural variables to
be positive, since an ordering of variables can be generated to render them in the
(k1)
form ykk
. Second derivatives of transforms with respect to intensive variables
!
for not give valid stability conditions. For example, the second derivative of A with
respect to the intensive variable T,
2 A
S
2 =
T V ,N
T V ,N
!
does not give a valid stability condition. This derivative is negative according to
Eq. 6.25. Only extensive variables provide stability conditions because they are the
only ones that obey conservation laws such as those given by Eq. 6.12.
Thus far, we have determined a set of n+1 thermodynamic derivatives that are
required to be positive for a stable n-component system. If we know that we are
already in a stable thermodynamic region, we now show that we can anticipate
which one of the n+1 thermodynamic stability conditions will be violated first
when approaching a limit of stability. We have seen in 4.5 that there is a step-
down relationship linking derivatives of successive transforms. Applying Eq. 4.31,
(k1)
(k2)
we can obtain ykk
in terms of ykk
:
!
!

(k1)
(k2)
ykk
= ykk
(y ) !!!!k > 2
(k2)
k1,k
(k2)
yk1,k1
(6.28)
We have already established that second derivatives of transforms with respect to

a single extensive natural variable are positive in a stable thermodynamic system.
(k2)
(k2)
Thus, we know that both ykk
and yk1,k1
are positive, since variables k and k1
!
(k2)
!
are untransformed (extensive) in the transform of order k2. If yk1,k1
were to
!
approach zero, then the second, negative term in Eq. 6.28 would dominate the sum

Beegle, B. L.; Modell, M.; and Reid, R. C., AIChE J., 20: 1200-6 (1974).
10/4/12 version
167
(k1)
and make ykk
itself to become negative. Thus, we conclude that derivatives of
!
higher-order transforms approach zero ahead of derivatives of lower-order trans-
forms, when starting from a stable region. Thus, we can establish that a single sta-
bility condition (the second derivative of the highest-order transform) is first vio-
lated on the limit of stability for a system of n components:
(n)
yn+1,n+1
> 0
We will first use this concept to identify a pecking order among stability con-
ditions for a one-component system. A condition corresponding to a first-order
transform, such as

2 A
P
P
(1)
y (0) = U(S,V ,N) y22
= 2 > 0 > 0 < 0 (6.29)
V T ,N
V T
V T ,N
!
is violated ahead of conditions corresponding to the basis function, such as

2 U
T
T
(0)
y (0) = U(S,V ,N) y11
= 2 > 0
>0
> 0
CV
S V ,N
S V ,N
!
(6.30)
Eq. 6.29 is called the condition of mechanical stability and implies that pres-
sure decreases as volume increases at constant temperature, or equivalently that
the isothermal compressibility T > 0. Eq. 6.30 is called the thermal stability condi-
tion. The constant-volume heat capacity remains finite at the limit of stability. An-
other key stability condition for a one-component system is obtained from the en-
thalpy first-order transform:

2 H
T
T
(1)
y (0) = U(V ,S,N) y22
= 2 > 0 > 0
> 0 (6.31)
CP
S P ,N
S P ,N
!
As will be shown in Example 6.3, the two conditions represented by Eqs. 6.29 and
6.31 are equivalent; they get violated simultaneously when a system reaches a limit
of stability.
For binary systems, the key condition that is first violated at a limit of stability
(2)
is the one resulting from y33
, e.g.:
!
2 G

(2)

y (0) = U(S ,V ,N1 ,N2 ) y33
=
> 0 1
> 0 (6.32)
2
N
N1 T ,P ,N
1 T ,P ,N
2
2
!
The condition of Eq. 6.32 is commonly used to determine whether a binary system
separates into two immiscible phases at a given temperature and pressure, as dis-
10/4/12 version
key stability
condition for
n-component
system
168
cussed in Chapter 9. Other equivalent key stability conditions for binary systems
include:

(2)
y (0) = U(S,V ,N2 ,N1 ) y33
= 2
> 0
N2 T ,P ,N
1
!
(2) T
y (0) = U(N1 ,N2 ,S,V ) y33
=
> 0
S , ,V
1 2
!
P
(2)
y (0) = U(N1 ,N2 ,V ,S) y33
=
>0
V , ,S
1 2

!
Example 6.3 Equivalence of stability criteria

Prove that the key stability conditions for a one-component system given by Eqs.
6.29 and 6.31 are equivalent, by expressing these two derivatives in terms of each
other.

The two relevant derivatives are:
2 A
2 H
P
T
1 P
1 T
T
and

=
=
=
= =
2
2
N V T
V T ,N
S P ,N S P ,N N S P NC P
V T ,N

!
!
Both are second derivatives of a fundamental equation with respect to one of its
natural variables. To express them in terms of each other, we need to introduce
another variable using the chain rule, Eq. 5.11:
P
P S

=

V T S T V T
!
(i)
The first term of the right-hand side of expression (i) can be obtained from the
XYZ-1 rule as:
P S T
P
T P
S T P = 1
S = S T
T P S
T
P S
inversion!rule
!
Substituting (ii) into (i):
P
T P S
P
T

V = S T V

T
P S
T
V T S P
!
!
10/4/12 version
(ii)
169
The two derivatives of interest are proportional to each other; when one of them is
zero the other one is zero as well.
Example 6.4 Heating on adiabatic expansion
In 3.1 it was suggested that, unlike ideal gases, some substances heat up when
expanded adiabatically. Express the relevant thermodynamic relationship in terms
of derivatives of known sign (as far as possible) and determine the requirements
on material properties for a substance to heat up when expanded adiabatically.

The relevant thermodynamic derivative for determining the adiabatic change of
temperature with volume is (T/V) S . We need to express it in terms of deriva-
tives that have known signs in stable thermodynamic systems. For this, we use the
chain rule (Eq. 5.11) and the triple-product rule (Eq. 5.12) to obtain:
(
(
)
)
)(
T / P
S / P T / S
T
S
T
P
=
=

V
S V / P
V / P
S
S
!
The denominator of the right-hand side of (i),
(i)
(V / P)S
!
is always negative, according to Eq. 6.18. The derivative
(T / S)P = (T / S)P.N
!
is always positive according to Eq. 6.26. The other derivative can be transformed
using Maxwells rule on G:
dG = SdT +VdP (S / P)T = (V / T )P = V P
!
Since the coefficient of thermal expansion P can be either positive or negative, the
derivative in (i) can have either sign. The more common (negative) sign occurs for
substances that have positive coefficient of thermal expansion P, while the oppo-
site is true for substances with negative P . Ideal gases always have positive coeffi-
cients of thermal expansion.
6.3 Fluctuations
Our discussion of equilibrium conditions in 6.1 has established that for a given set
of external variables (or constraints) on a system, the corresponding Legendre
transformation is minimized or maximized at equilibrium, depending on whether
the starting point was the energy of the entropy. In the previous section, we
analyzed stability from a macroscopic point of view, establishing sets of stability

10/4/12 version
170
conditions for thermodynamic systems expressed as second derivatives of

thermodynamic potential functions. At a microscopic level, even for a stable
thermodynamic system, the unconstrained variables of a system undergo
continuous fluctuations around their mean values. These fluctuations will turn out
to be intimately linked to the second derivatives of the corresponding partition
function for the relevant statistical ensemble.
As a first step, let us compute the mean-squared fluctuation of energy in the
canonical (NVT) ensemble. In this ensemble, probabilities of microstates are:
exp U
P =
!!!!!where!!!!!Q (N ,V ,T ) =
exp U
Q
all!microstates!!
!
The mean-squared fluctuations of energy are:

(U)2 = (U U)2 = U 2 2UU + U2 = U 2 U2 =

=
PU 2
all!microstates!

PU
all!microstates!
The sums can be related to the first and second derivatives of !Q (N ,V ,T ) :
=
N ,V
all!microstates!!
2 Q
=
2
N ,V
!
U exp U = Q
all!microstates!!
U 2 exp
( U ) =
PU
all!microstates!!
Q
PU 2
all!microstates!!
So that:

1 2 Q
(U) = 2
Q
N ,V
!
2
1 Q
2 lnQ
U
=
=

2
Q
N ,V
N ,V
N ,V
The last equality results from the fact that the logarithm of the canonical partition
function is the first Legendre transform of S /kB . Now using the definition of the
!
heat capacity at constant volume,

U
(U)2 = kBT 2
= kBT 2NCV
T N ,V
!
(6.33)
This is a remarkable result. We have obtained a relationship between the

thermodynamic parameters of a system and the magnitude of spontaneous fluctu-
ations. In the language of Legendre transformations, we have shown that for
y (1) = lnQ = y (1)(,V ,N) , the mean-squared fluctuations of the energy are equal
!
(1)
to the corresponding second derivative, y11
.
!

10/4/12 version
171
6.3 Fluctuations
It is interesting to note that the heat capacity of the system, CV, is an intensive
variable (independent of the size of the system), so the absolute magnitude of the
mean-squared fluctuations grows linearly with system size. However, more rele-
vant is the magnitude of the fluctuations relative to the mean energy of the system:
(U)2
=
U
kBT 2NCV
U
N
1
=

N
N
(6.34)
23
For a macroscopic system, N = O(10 ), so the relative fluctuations are extremely

small on average: the energy of an ideal gas system at equilibrium with a room-
11
temperature bath is constant to roughly 1 part in 10 . However, simulations are
often performed with very small systems having as few as 100 molecules. The
thermal energy of molecules is of O(kBT), and the heat capacities are of O(kB), so
typical relative fluctuations in energy are of the order of 10%.
We can easily generalize the fluctuation relationships to other ensembles. For
example, in the grand canonical (VT) ensemble for a one-component system, fluc-
tuations in the number of molecules are obtained from the second derivative of the
partition function of the ensemble (see 5.5):
y (0) = ln(U ,N ,V )!!;!!y (2) = ln(,,V )

2 ln
N
N
(2)
(N)2 = y22
=
=
=
k
T

B
2
() ,V () ,V
T ,V
!
(6.35)
Similarly, fluctuations in the total volume of a system under NPT conditions

can be obtained as follows:
y (0) = ln(U ,V ,N)!!;!!y (2) = ln(,P,N)

2 ln
V
V
(2)
(V )2 = y22
=
=
= kBT
2
(P) ,N
P T ,N
(P) ,N
!
(6.36)
It is interesting to note that there is a direct connection between microscopic

fluctuations and stability conditions. Fluctuations of the energy in the canonical
ensemble were found to be proportional to the heat capacity at constant volume,
which is positive for stable thermodynamic systems. Fluctuations of the number of
molecules in the grand canonical (VT) ensemble, and of the volume in the NPT
ensemble, are also proportional to derivatives that are positive for stable systems.
Moreover, these latter derivatives diverge at a limit of stability for a one-
component system. Thus, the microscopic interpretation of the loss of stability is
the development of unbounded fluctuations within a system. Conversely, one can
interpret the macroscopic stability conditions as having a positive sign because
they represent mean-squared fluctuations, quantities that are necessarily positive
in sign.
10/4/12 version
172
Example 6.5 Fluctuations involving uncorrelated particles**

Compute the mean-squared fluctuations in the number of particles for an open
system at a very low density ! = N /V , for which the particles can be considered
to be uncorrelated. Obtain the equation of state for such a system.

We divide an open system of total volume V, containing <N> particles on average,
into !m N subcells, so that each one of them unlikely to contain more than one
particles at any given time. We denote by ni the cell occupancy of subcell i, with
!
m
ni = 0!!or!!1,!!!and!!! n i = N
i=1
!
The mean-squared fluctuation of the total number of particles in V is:
(N)2 =
!
( N N)
= N 2 N2 = ni n j ni n j
By interchanging the averages and the sums (since average of a sum is always
equal to the sum of averages),
m m
< (N)2 >= < ni n j > < ni >< n j >

i=1 j=1
!
Since two different cells are completely independent, we must have
< n n >=< ni >< n j > for i j and the only terms that do not cancel out in the double
! i j
sum are ones with i = j :
m
< (N)2 >= (< ni2 > < ni >2 )

i=1
!

Since ni = 0 or 1, ni2 = ni , so that
m
(N)2 = ni ni 2 = m ni ni 2 = m n1 (1 n1 ) m n1 = N
i=1
From this equation and the general expression for fluctuations in the grand canon-
ical ensemble, we can obtain information on the thermodynamic functions of the
system:
(N)2 =
1 N

= N
,V

** Following 3.6 in Chandler, D., Introduction to Modern Statistical Mechanics, Oxford Univ.
Press, 1987.
10/4/12 version
173
6.3 Fluctuations
Dividing by V and taking the reciprocal, with ! = N /V

1
= = = constant + ln
,V

This is the expression in classical thermodynamics for the chemical potential for
an ideal gas. From !d = dG = SdT +VdP , with = 1/V, = 1/kBT

P
1 P
1
= = P = + constant
The integration constant for P is 0 since at = 0, P = 0. Eq. [33] is then just the ide-
al gas law:
P = PV = NkBT , (where N is the number of molecules, not moles)

!
The purpose of this example is to show that very simple microscopic assumptions
(independence of all particles) result in useful, experimentally valid expressions
for the macroscopic thermodynamic behavior.

6.4 Maxwell Construction, Binodals and Spinodals

When pressure is plotted against the specific volume, experimentally deter-
mined isotherms for many systems follow paths similar to those shown in Fig. 6.7,
with a horizontal portion marking a phase transition, defined as a sharp disconti-
nuity in a thermodynamic proper-
ty. For this specific example, the
low-volume, high-pressure phase
on the left branch of the isotherm
is a liquid, and the high-volume,
low-pressure phase on the right
branch a vapor, so the horizontal
portion corresponds to vaporiza-
tion of the liquid or condensation
of the vapor. Provided that care is
taken to eliminate sources of nu-
cleation, the liquid and vapor iso-

therms can be measured into the
Figure 6.7 Schematic of an experimentally de-
metastable regions, indicated by
termined isotherm for a system with a liquid-
the dashed lines in Fig. 6.7. The vapor phase transition. Dashed lines are metasta-
ble extensions of the liquid and vapor branches.
saturated liquid and vapor phases
are at the two ends of the horizon-
10/4/12 version
174
tal line segment. Thermodynamic

theories and engineering equa-
tions of state of the type discussed
in the next chapter, on the other
hand, produce isotherms that con-
nect the liquid and vapor branches
by a smooth curve, as shown in
Fig. 6.7. This curve is called a van
der Waals loop. The points marked
1 and 2 in this figure are limits of
stability, since for these points,

Figure 6.7 Schematic of a model or equation-of-
state isotherm for a system with a phase transi-
tion. The stability condition is violated along the
dotted line.

P
V = 0
T
!
(6.37)
The van der Waals loop violates the mechanical stability condition, Eq. 6.24, along
the dotted line between points 1 and 2. We know that real systems cannot exist at
such states, but the presence of a continuous path between phases in equation-of-
state isotherms provides a mechanism for satisfying the conditions of equilibrium.
In other words, we can use the model isotherm of Fig. 6.7 to determine the points
along it that satisfy equality of chemical potentials, L = V . Starting from the fun-
damental equation for the Gibbs free energy, for
any two points along an isotherm,

(6.38)
P = V = V dP
T
!

In order to see what this relationship im-

plies, let us flip the axes of Fig. 6.7 to obtain Fig.
6.8. We now draw a vertical line that leaves
equal areas to the left and right of it, as shown in
the figure. For equal areas, the integral of !VdP
from point A to point B is zero, so Eq. 6.38 sug-
gests that the chemical potentials are equal at A
and B. These two points also have equal pres-
sures (being on the same vertical line) and equal
temperatures (being on the same isotherm).
They satisfy the conditions of phase coexistence
(Eq. 6.5) and the coexisting phases can now be
identified as A L (saturated liquid) and B V

10/4/12 version
Figure 6.8 Maxwell construction.
6.4 Maxwell Construction, Binodals and Spinodals
175
(saturated vapor). This procedure is known as Maxwell construction, named after

the Scottish physicist James Clerk Maxwell who first proposed it. Line segments 1A
and 2B (dashed) are metastable states, satisfying the stability condition but be-
yond the points of stable equilibrium. They correspond to the dashed extensions of
the stable liquid and vapor branches seen in experimental systems (Fig. 6.7, p.
173).
The densities and other properties of coexisting phases depend on tempera-
ture. For the vapor-liquid transition, the two phases become increasingly more
similar as temperature is raised. At a very special location in thermodynamic co-
ordinate space called the critical point, the properties of the two phases at coexist-
ence become identical. Such critical points are seen not only for vapor-liquid tran-
sitions, but for liquid-liquid equilibria as well. Many other physical phenomena can
be described as phase transitions ending at critical points for example, the Curie
point, a temperature above which magnets lose their ability to retain a permanent
magnetization, is also a critical point.
A schematic phase diagram showing two subcritical isotherms as well as the
critical isotherm is presented in Fig. 6.9. As previously, stable segments of the iso-
therms are shown as continuous lines, metastable segments shown as dashed
lines, and unstable segments as dotted lines. The coexistence points are obtained
from Maxwell constructions at each temperature. The locus of coexistence points
defines the vapor-liquid coexistence envelope, which is also known as the binodal
curve. The locus of stability limits (points along which the condition of zero deriva-
tive of the isotherms, Eq. 6.37, holds) define the spinodal curve and the region
within this curve is known as the spinodal region. The spinodal curve is entirely
within the two-phase equilibrium (binodal) curve; the two meet at the critical
point. Within the spinodal region (horizontally hatched area), the system is unsta-
ble with respect to phase separation; real systems rapidly form two phases, in a

Figure 6.9 Spinodal (horizontally hatched) and metastable (diagonally hatched) regions with-
in the coexistence (binodal) curve.
10/4/12 version
176
process known as spinodal decomposition. The two diagonally hatched areas be-
tween the spinodal and binodal curves are metastable regions for the liquid (left,
low V ) and gas (right, high V ). In these regions, formation of a two-phase system is
thermodynamically favored but requires nucleation and growth of the new phase.
As discussed in 6.2, the vanishing of the first derivative of the pressure with
respect to volume defines a limit of stability because it corresponds to a second
derivative of the Helmholtz free energy A. However, at the critical point, the se-
cond derivative of the pressure with respect to volume also vanishes this is be-
cause the critical point represents the merging of a maximum and a minimum of
the P versus V isothermal curves. At a minimum (left side of the spinodal in Fig.
6.9) the second derivative is positive and at a maximum (right side of the spinodal)
the second derivative is negative. Since the isotherm itself is continuous and has
no discontinuities in its derivatives, this can only happen if the second derivative is
zero at the critical point. Stability requires that the next derivative (third deriva-
tive of pressure with respect to volume) is positive, a condition satisfied at the crit-
ical point. The criticality conditions are then:
P P 2
V = 2 = 0
T V T
!
(6.39)
We have shown in Example 6.3 that the two stability conditions:

P
T
> 0 and
< 0
CP
V T
!
are equivalent. Therefore, at any critical point,

P
T
V = 0 C = 0 CP
P
T
(6.40)
Many other physical quantities diverge at critical points. For example, density fluc-
tuations in a normal liquid or gas are correlated only over length scales compa-
rable to the size of molecules and thus much shorter than the wavelength of light.
Near critical points, the correlation length for density fluctuations increases rapid-
ly and becomes much bigger than molecular size. This gives rise to a characteristic
milky appearance of fluids near criticality, known as critical opalescence.
6.5 Gibbs Phase Rule

The equilibrium criteria of Eq. 6.5 are that pressure, temperature and chemical
potential for each component should be uniform throughout a system at equilibri-
um. We know from everyday experience that multiple phases of different densities
10/4/12 version
177
can exist at different conditions for example, water is found in nature as solid ice,
liquid water and vapor. In 6.3 we suggested that two phases could coexist for a
range of temperatures at a specific pressure for one-component systems. An inter-
esting question with important practical implications is whether the conditions of
equilibrium impose restrictions on the number of possible phases that can simul-
taneously be present in a system at equilibrium. The answer turns out to depend
on the number of independent chemical species (components) in a system, in a
relationship first proposed by J. Willard Gibbs in 1870.
We have seen in Chapter 5 that n+2 thermodynamic variables are required to
fully specify the state of a thermodynamic system. These could be selected as
(T,P,N 1 ,N 2 ,,N n ). Dividing the molar amounts by the total number of moles in
the system, N = N 1 +N 2 ++N n , we can express thermodynamic properties in terms
of (T,P,x 1 ,x 2 ,,x n1,N). However, if we restrict our attention to just intensive
properties, we can eliminate N from the variable set and express these properties
in terms of n+1 intensive variables, (T,P,x 1 ,x 2 ,,x n1). Now consider a system
with phases coexisting at equilibrium. We denote by x i , j the mole fraction of
component i in phase j and by i , j the chemical potential of component i in phase j.
The conditions imposed by equilibrium on the chemical potentials at coexistence,
Eq. 6.6, can now be written as:
1,1 = 1,2 = = 1,
2,1 = 2,2 = = 2,
(6.41)
= n,2 = = n,
! n,1
There are !n( 1) independent equations in this set of relationships. Each of
the chemical potentials in Eqs. 6.41 can be written as a function of the tempera-
ture, pressure and composition variables in each phase:
1,1 = 1,1 (T ,P,x1,1 ,x2,1 ,x n1,1 )

2,1 = 2,1 (T ,P,x1,1 ,x2,1 ,x n1,1 )
n,1 = n,1 (T ,P,x1,1 ,x2,1 ,x n1,1 )

1,2 = 1,2(T ,P,x1,2 ,x2,2 ,x n1,2 )
2,2 = 2,2(T ,P,x1,2 ,x2,2 ,x n1,2 )
= n, (T ,P,x1, ,x2, ,x n1, )

! n,
10/4/12 version
(6.42)
178
Thus, there are !2+(n 1) intensive variables describing the chemical po-
tentials, the common T and P as well as (n1) mole fractions for each phase. But
these are not all independent, as they must satisfy the !n ( 1) relationships of
Eq. 6.42. The number of independent intensive variables, which is defined as the
number of degrees of freedom, F , of the system is:
F = !{number!of!total!variables}! !{number!of!constraints}!
F = 2+(n1) n( 1) = 2+ n n + n
!F = n + 2

Gibbs
(6.43) phase rule
Phase diagrams of pure components often contain multiple solid phases (pol-
ymorphs), as illustrated in Fig. 6.10, which shows a partial high-pressure phase

Figure 6.10 Partial phase diagram of water at high pressures. Triple points are shown as
circles. Data are from Revised Release on the Pressure along the Melting a nd Sublimation
Curves of Ordinary Water Substance, International Association of Properties of Water and
Steam, (2008) and L. Mercury et al., Thermodynamics of ice polymorphs and `ice-like' water
in hydrates and hydroxides,, Appl. Geochem. 16, 161-181 (2001).
10/4/12 version
179
diagram of water, including multiple solid polymorphs. Ice formed from liquid wa-
ter at near-atmospheric conditions is hexagonal ice Ih.
The phase rule does not impose a limit on the number of possible phases pre-
sent in different locations of the phase diagram, it only restricts how many can co-
exist at any given temperature and pressure. As suggested by the phase rule, areas
in this diagram contain only a single phase (F = 2, two degrees of freedom, corre-
sponding to two-dimensional geometric objects), while lines (F = 1) correspond to
coexistence of two phases. Three phases coexist at triple points (F = 0). A one-
component system cannot exist as four separate phases at any point in the phase
diagram, as this corresponds to negative (unfeasible) degrees of freedom.
Another case of interest is binary systems. Intensive variables of interest for
binary systems are the temperature, pressure and composition (mole fraction of
one component). Single phase, two-component systems have F = 3, three degrees
of freedom, corresponding to volumes in the three-dimensional space of the inten-
sive variables. Application of the phase rule to two-phase systems gives F = 2, two
degrees of freedom, so that at a given temperature and pressure a range of compo-
sitions can exist. For three-phase systems, there is a line of triple points (F = 1),
along which temperature, pressure and composition varies.
The conditions of criticality (Eq. 6.39) impose two additional constraints on an
otherwise one-phase system, thus using up two degrees of freedom. Thus, for a
one-component system the number of degrees of freedom at criticality is zero, so
we are justified to talk about a critical point. For two-component systems, there is
a critical line along which the critical composition, pressure and temperature vary.
10/4/12 version

Symbols and Units: Script Fonts Are Used For Physical Quantities and in Bold Font

Hochgeladen von

Dokumentinformationen

Originaltitel

Copyright

Verfügbare Formate

Dieses Dokument teilen

Dokument teilen oder einbetten

Freigabeoptionen

Stufen Sie dieses Dokument als nützlich ein?

Sind diese Inhalte unangemessen?

Copyright:

Verfügbare Formate

Symbols and Units: Script Fonts Are Used For Physical Quantities and in Bold Font

Hochgeladen von

Copyright:

Verfügbare Formate

Symbols

Helmholtz free energy [J (kg m2 )/s2]

Symbols and Units

Symbols Latin alphabet (cont.)

expansion ratio [dimensionless]

Symbols and Units

Symbols Greek alphabet (cont.)

inverse temperature, 1/kBT [J1]

Symbols and Units

infinite-dilution property: superscript

indicates a set of independent mole numbers or mole fractions of compo-

The branch of physical science concerned with equilibrium in material

The study of restrictions on the physical properties of matter that follow

without making any assumptions about the microscopic constitution of matter.

How much work is needed to compress a gas?

At a particular temperature and pressure, will a certain liquid vaporize?

How far will a chemical reaction proceed in a vessel of known volume

How can we modify a protein in order to maximize its thermal stability?

Under what conditions will a certain surfactant form micellar aggregates?

Are two polymers compatible (miscible) with each other?

For many of the questions above, other considerations, such as inefficiencies in

1.2 Thermometric and Ideal-Gas Temperature Scales

1.2 Thermometric and Ideal-Gas Temperature Scales

A thermometric temperature scale can be established by defining a standard

Figure 1.2 Volumetric properties of low-pressure gases.

ture, as shown schematically in Fig. 1.2:

The relationship between thermodynamic and Celsius temperature scales is:

T [K] = [C] + 273.15

In many problems in this book we will perform calculations to 3 significant figures,

1.3 Systems and Boundaries

1.3 Systems and Boundaries

Rogers, W. A. et al., "Diffusion Coefficient, Solubility, and Permeability for Helium in

1.4 Equilibrium States

For closed systems with no internal boundaries and containing known

1.4 Equilibrium States

Chapter 2. Work, Heat, and Energy

2.1 Mechanical Work

2.1 Mechanical Work

In 1845, James Joule performed ex-

system with hysteresis.

Chapter 2. Work, Heat, and Energy

Figure 2.4 Piston-cylinder system with gradual lifting.

2.1 Mechanical Work

2.2 First Law for Closed Systems

Chapter 2. Work, Heat, and Energy

This equation states simply that the change of en-

If z2 < z1 , work is positive, as it is performed on the system of interest by the ex-

The internal energy, denoted by the symbol U, is due to microscopic interac-

2.2 First Law for Closed Systems

simplicity, we often omit the internal

Example 2.1 A stretched rubber band

Chapter 2. Work, Heat, and Energy

ty, C = (U / T)l of the rubber band is 5 J/K, approximately independent of length.

2.2 First Law for Closed Systems

the right, Patm ; a net force to the right is re-

!!!!(787.36 0.0181)10 m /mol!

Wsys = P VPA x = P VP V = 2.47!kJ/mol

W is negative because expansion of the system means it performs work on its

First Law balance for the closed system now gives:

U = Q +Wsys Q = U Wsys = U V U L Wsys = (41.52+ 2.47)!kJ/mol = 43.99!kJ/mol

!= (37.60+ 3.05)!kJ/mol = 40.65!kJ/mol

Chapter 2. Work, Heat, and Energy

2.3 First Law for Open Systems