Beruflich Dokumente
Kultur Dokumente
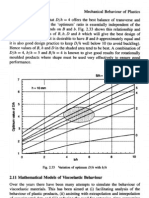
Drilling DOF
Hochgeladen von
Daniele Di LucaCopyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Drilling DOF
Hochgeladen von
Daniele Di LucaCopyright:
Verfügbare Formate
Computer methods
in applied
mechanlcs and
englnrfwlng
ELSEVIER
Comput. Methods Appl. Mech. Engrg. 143 (1997) 1-11
A new finite element with drilling D.O.F.*
C. Chinosi,,
M.I. Comodi, G. Sacchib
Dipartimento di Matematica, Vniversitri di Pavia, 27100 Pavia, Italy
hlstituto di Analisi Numerica de1 CNR, 27100 Pavia, Italy
Received 27 January 1995; revised 11 January 1996
Abstract
The aim of this paper is to study a new finite element with drilling degrees of freedom for linear elasticity problems and to
show its convergence properties. We will compare this element on a test problem with the corresponding drill-element introduced
by Hughes and Brezzi and we will analyze the behaviour of both with respect to the stiffening effect.
1. Introduction
In this paper we will deal with the approximation of the linear elasticity problem by means of finite
elements with drilling degrees of freedom. This argument was initially studied by a group of engineers
using traditional theories (see for instance [l-3] and the references there given). Recently, some new
approaches have been presented which have newly stimulated the interest of both mathematicians and
engineers in this field (see for instance [4-61 and the references there given). In these works the drilling
rotations are introduced as independent variables and a displacement-type formulation can be obtained
using suitable variational principles. In this paper, following the formulation introduced by Hughes and
Brezzi in [5], the linear elasticity problem is written in an unconventional way assuming the stresses to
be non-symmetrical and introducing the rotations as independent variables with the role of Lagrange
multiplier for the symmetry constraint. In this case the unknowns of the problem are the displacements,
the rotations and the stresses. When a standard mixed approximation of the problem is used one might
lose some ellipticity properties of the formulation obtaining as a result an unstable numerical scheme.
In order to resolve this problem the original mixed variational principle can be modified improving the
stability properties of the approximation scheme. This modified mixed formulation can be treated with
different finite element schemes related to different approximations of the stress field.
In this work we are interested in the construction of new finite element schemes, in their
implementation and application to the solution of standard elasticity problems in order to analyze the
behaviour of the approximation obtained also with respect to certain stiffening effects which could be
introduced by this modified formulation (see [5]).
First of all, we should refer to the displacement-type scheme introduced by Hughes and Brezzi [5,7]
in which the stress field is eliminated through an a priori satisfaction of the Euler-Lagrange
conditions.
In the implementation
of the resulting element continuous linear polynomials are used in the
* Corresponding author.
* Work partially supported by M.U.R.S.T.,
Italy, and by C.N.R., Italy.
0045-7825/97/$17.00 0 1997 Elsevier Science S.A. All rights reserved
PII SOO45-7825(96)01148-6
i Cotnpur. Method3 Appl. Mrch. Engrg. 143 (1997) 1-I I
C. Chinosi et al.
approximation
of both displacements
and rotations.
Consequently,
the symmetrical
part of the stresses
is approximated
by constants,
whereas the skew-symmetrical
part is discretized
by polynomials
of
degree less than or equal to one. The new element we are dealing with gives an approximation
of the
stress field by means of trial functions related to the Raviart-Thomas
space [S]. More precisely,
the
displacements
and rotations
are approximated
as for the element
previously
described,
whereas the
stress field is discretizhd
using the Cartesian
product of the Raviart-Thomas
space with itself. This
formulation
still leads to a displacement
scheme, which however seems to be less sensitive
to the
stiffening effect.
An outline of the paper is as follows. In Section 2 we will present the mathematical
formulation
of
the elasticity problem, its mixed variational
formulation
and its displacement-type
formulation.
Section
3 will deal with the construction
of the finite element schemes and in Section 4 we will compare the
numerical
results obtained on a test problem.
In Section 5 we will draw some conclusions.
2. Problem
formulation
We have considered
the linear
elasticity
problem
in the following
way:
Find U, 9, a such that)
diva +f= 0
skew a = 0
(2.1)
in0
$I = skew Vu
symm a = c. symm Vui
u = 0
on 4,
an=honf,.
where i1 is an open set of 1w with a piecewise smooth boundary
r = 4, U T,; r, II r, = 0, n is the
outward normal to r; h is the vector of the tractions; f is the body force vector; u is the displacement
vector; (I, is a skew-symmetric
tensor representing
the rotations
and _o is the stress tensor; c = [c~,~~],
i, j, k, 1 E 1,2 is the elastic modulus that in the isotropic case and for plane stresses has the following
expression
UE
E
c,,ii=(1_u)~,,6,,+2(1+u)
(8.rk1I6 +
s;,s,,)
(2.2)
E being Youngs modulus,
v Poissons ratio and a,, Kronecker
delta. The notation
c *z indicates the
7 .u will indicate the scalar product of tensors: -T *CT= ~;~a~,,
product:
c a~= c+,rkkr and the notation
where (and from now on) the index-free
notation is used (see [2]).
2.1.
Modified variational formulation
For the sake of simplicity let us consider problem (2.1) using Dirichlet boundary
conditions.
More
general
boundary
conditions
provide
no essential
difficulties
and can be handled
using standard
arguments
(see [2,9]). As the standard mixed formulation
of problem (2.1) leads to an unstable method
Hughes and Brezzi [5] suggested
a modified
variational
formulation
which improves
the stability
properties
of the discrete approximation.
Let V, W. T be the following spaces:
v=
{u/u E (H:,@))}
W = {wlw E (L(R)),
(2.3)
symm w = O}
(2.4)
T = (111 E (L(O))}
Let us consider
the potential
(2.5)
energy
functional
II:
C. Chinosi et al.
I Comput. Methods Appl. Mech. Engrg. 143 (J997) I-I I
Il.VxWxT+R,
rt. (Vu -w) dx - J-, uf d.r .
i R-
H(u, w, -7) = - + n symmz.c-*symmIdr+
i
In order to obtain a more stable formulation
II,:
(2.6)
of the problem we can consider the following functional
I&:VxWxT+R,
(2.7)
I&(u,~,~)=n-~~-
n(skew~/2dx
which represents a perturbation of II by means of a parameter y to be chosen in a suitable way.
Introducing the functional fly one can get the following variational formulation
Find (u, -4, _a) E V
T such that
&T,T)+&,(~,ICI))=O
-
VTET
Ha, (UTw)) = (.A (u, w))
v (u, w) E v x w
(2.8)
where
a(a, 2) = -
b(a, (u, w)) =
syrnrna.c-.
I (Tf.
R-
symmxdx-y-l
(Vu -s)
skew a * skew 1 dx
(2.9)
(2.10)
dx
(2.11)
(A (u, w)) = I, uf ~ .
It is easy to show (see (51) that the formulation
related to the use of the functional n.
2.2. Displacement-type
(2.8) is equivalent to the standard mixed formulation
variational formulation
In this section we briefly recall the variational formulation of problem (2.1) as introduced in [5]. Let
us consider the modified variational formulation (2.8) and let us eliminate the stresses by imposing:
symm_7=c.symmVu,
skew z= -y(skew
(2.12)
Vu -w) .
We obtain the following functional:
rrY:VxW-+R,
(2.13)
1
which leads to the following displacement-rotation
/I,(skewh-~~d.x-~~ufd.x
formulation
Find (u, -$) E V x W such that
+,ICI;v,w)=(f,(u,w))
-
(2.14)
V(~,!!!)EVXW
with
+g;n,!?)=
n symm Vu . c. symm Vu dr +
(skew Vu -?)(y(skew
Vu -411)) dr
(2.15)
C. Chinosi et al. I Comput. Methods Appl. Mech. Engrg.
143 (1997)
1-11
3. The approximation problems
In the following we shall describe the construction of the finite element schemes in order to solve
problems (2.8) and (2.14). For each element the interpolation spaces and the corresponding set of
degrees of freedom will be analysed. The discrete formulation of the problem will also be discussed in
terms of the evaluation of the elementary matrices related to each element.
3.1. The approximation of the problem (2.14):
a displacement-type formulation
Let & be a regular and quasi-uniform triangulation of 0 by triangles K whose maximum diameter is
less than h and let V,, W,, be finite dimensional subspaces of V, W, respectively. The discrete problem
corresponding to (2.14) is:
Find (u, -$/1) E V, x W,, such that
Z(u, -rClh;Uh, w) = (f, (u, w))
v (uh, PJ) E v, x w,
(3.1)
A convenient choice for the interpolation spaces leads to the approximation of both displacements and
rotations with standard, continuous, complete kth-order polynomials over straight-edged triangles.
Referring to the approximation of the stress field we can observe that (2.12) allows us to discretize both
the symmetrical and the skew-symmetrical part of the stress, respectively. One can then approximate
the displacements and the rotations with polynomials of first order. This leads to discretize the
symmetrical part of the stresses by constants and the skew-symmetrical part by polynomials of degree
less than or equal to one. The resulting finite element corresponds to the one introduced by Hughes and
Brezzi.
The approximation spaces used are
v, = {u]u E (C(0)),
W, = {w/w E (C(n)),
VKEY,,,
u,~E(P,(K)),
wlk. E (P,(K))J,
u=Oon
q,},
V K E 5,,, symm 3 =
(3.2)
0} ,
(3.3)
where P,(K) is the space of polynomials of degree less than or equal to one on K. In this case the
following theorem holds (see (51 Theorem 3.1).
THEOREM
3.1. The problem (3.1) has a unique solution (uh , $,) E V, X W,. Furthermore,
V x W is a sufficiently regular solution of (2.14), then
if (u, -$) E
(3.4)
where C(u, (cl) is a constant independent
of h.
In Fig. 1 we can see the previously introduced finite element (named DRILL) with the set of its d.o.f.
0
Fig. 1. The DRILL element
displacement
rotation
d.o.f.
d.o.f.
C. Chinosi et al. I Comput. Methods Appl. Mech. Engrg. 143 (1997) l-11
Writing problem (3.1) with matricial notations we obtain:
(3.5)
where d and 8 are, respectively, the nodal displacements and the nodal rotations; F is the nodal force
vector; ?? is the usual stiffness matrix due to the displacement interpolation and K,, , K,2, K,, are the
stiffness contributions of the term containing y in (2.15).
3.2. The approximation of the problem
(2.8)
using the Raviart-Thomas
space
In this section we will describe how a new displacement-type approximation of problem (2.1) can be
obtained. We will consider problem (2.8) and we will write its discrete formulation without eliminating
the stresses. In this case practical considerations dictate the stresses to be interpolated discontinuously.
With this assumption one can get a displacement type approximation scheme in which the stress field is
independently defined on each triangle. Let V,, W,, and T,, be finite dimensional subspaces of V, W and
T, respectively; the discrete problem corresponding to (2.8) is
Find (r/, -Jlh, _ah) E Vh x W,, x T,, such that
a@,
xh) + b@,
(uh, 2)) = 0
b(_ah,(u,Wh))=(f,(Uh,Wh))
V -7hE T,,
(3.6)
v(&?h)EVhXW&
Since we are interested in using the same interpolation spaces as in (3.2), (3.3) for displacements and
rotations, a suitable choice for the space T,, can be represented by the Raviart-Thomas
space of degree
zero. More precisely, the four components of the stress tensor are discretized by means of the Cartesian
product of the Raviart-Thomas
space (see [S]) with itself. So we define:
Th = {Z]Z E (L2(fl))4, zIK E (R&(K))*,
where RT,,(K)
v K E y/,h>,
is the space of Raviart-Thomas
(3.7)
polynomial vector fields:
RT,(K) = {P = (ply p2), p1 = a + bx, p2 = c + by, a, b, c ER}
(3.8)
With these choices one can prove the following theorem:
THEOREM
3.2. The problem (3.6) has a unique solution (uh, &,, a)
(u, p, _a) E V x W x T is a sufficiently regular solution of (2.8), then
llu -
E V,, x W,, X T,, . Furthermore,
~llv+ 119
-&Iv + lb -ahll, GW&_a)h 9
where C(u, -JI, cr) is a constant independent
if
(3.9)
of h.
PROOF. This result is similar to the one obtained in Theorem 3.1 for the DRILL element. The proof
of this theorem follows on from Theorem 2.2 in [5]: indeed, the continuity of the bilinear forms a(*, *)
and b(*, a), the T,-ellipticity of a(., a) and the inf-sup condition associated with the form b are
obviously satisfied. We now have to prove the following interpolation estimates: for each sufficiently
regular (v, w, I) E V X W X T, there exists (v, rjh, fh) E V, x W, x Th such that
jIu-GhIly4c(u)h,
(3.10)
(Iw -G, ]Iw s c(@r* ,
(3.11)
11~-z 11i- c c($h >
(3.12)
where c(u), c(w) and c(l) are independent of h.
The results (3.10) and (3.11) follow on from the standard results on finite element approximation.
prove (3.12) we will introduce a linear operator (see [S]) II, defined as follows:
To
C. Chinosi et ul. ! Compur. Methods Appl. Mech. Engrg.
II,, :
(H(R))-
14.3 (1997)
l-11
T,,
(3.13)
(3.14)
U&Z) /R = I&_71K
II,
satisfies.
for each side K of K, the following
R, (I&Z -I),,+/,
V q, E P,,(K).
dy = 0
relations:
(3.15)
i = I,2
being n = (n, , rzi) the unit outward normal to each side K of K.
We can observe that (see [8]), f or each 2 E (H(K)),
the relation
(3.14) uniquely
determines
a
function
II,? E (RT,,(K)).
moreover
using the same arguments
as in [S] we can get the following
approximation
result:
]I&~ -~11,,.~~ ~cchl~],.,,
v-r smooth
enough
with c independent
of h; then (3.12) holds. This result allows us to apply the Theorem
to the error estimate (3.9).
Cl
2.2 in [5] leading
REMARK.
Comparing
the two formulations
(3.1) and (3.6) one can see that, in essence, (3.1) uses a
discontinuous
stress field of local degree one (in contrast with the usual displacement
formulation,
which amounts to use a discontinuous
stress field of local degree zero) while (3.6) corresponds
to a
choice of the local stress field intermediate
between P, and P,, (based on the Raviart-Thomas
space
RT,,) thus naturally
reducing
the stiffening
effect induced by (3.1). A similar result can easily be
obtained for higher degree elements:
when the usual displacement
formulation
with local degree k + 1
(for displacements)
implicitly uses stresses of local degree k, the formulation
of [.5] uses a local stress
field of degree k + 1. The analogue of (3.6) would then use a local stress field intermediate between Pk
space RT,).
As it can easily be seen from the proof of
and P,+, (based on the Raviart-Thomas
Theorem 3.2, which immediately
generalizes
to an arbitrary order k, these new spaces (based on RT,)
for the stresses are somehow the minimal ones that can guarantee
stability and convergence
with
optimal error estimates,
that would not be obtainable,
for the formulation
(3.6), with stresses of local
degree k (zero in our case).
Let us now come back to the formulation
(3.6), in order to see how a convenient
implementation
of
it (through a suitable elimination
of the stress field) can reduce the problem to a form very similar to
(3. l), only with a minor additional
effort in the computation
of the local stiffness matrix. Let us write
the bilinear form ~(_a, I) in the following way:
U(El ,xh)=where
a.m.rl&,
_
I f1 -
(3.16)
m = [wz,,~,], i. j, k, I = 1,2 is a symmetric
T,ki =
+I2
related
to c-~ and y
c,,:,fori=jork=I
1+v
= mzlzl =2E+
m211: = ml121
Moreover,
tensor
(3.17)
1+v
E--P
2E
7-l
2
we have
b(q, (u, If,) =
J!
z/2. ((Vu)+g, d-x
(3.18)
m.IJLm~.
f1
Let us split _o into two parts
((Vu)+I&)d.x
C. Chinosi et al. I Comput. Methods Appl. Mech. Engrg.
143 (1997)
l-11
we obtain, from (3.16) and (3.18), using the first equation of (3.6)
h
_a,,=m-.((vuh),
from which
symm _a: = c. symm Vuh ,
(3.19)
skew _ah,= -y skew Vuh ,
and
-y$i). m
R (ah, -
(3.20)
.xh dx = 0
Substituting (3.19) in the second equation of (3.6) and using (3.20), the discrete problem (3.6) becomes
Find (Us, I,!J)E V,
W, such that
symm Vuh . c. symm Vvh dx + y
IR
IR
(3.21)
V vh E Vh
-Y I skew Vvh$h
- dx = (f, u)
R
-y
skew Vuh skew Vvh dx
skew Vuh~h dx +
VWhEWh.
Observe that the matricial formulation of this problem differs from the formulation (3.5) related to the
DRILL element uniquely for the matrix K,,. We provide now the construction of this matrix on a single
triangle K E ,Th. We have
[K,Jij=j
_ah,,&dx,
i,j=1,2,3
(3.22)
where {wi} are the basis functions on K for the rotations space:
w =
-[
-A
(3.23)
being {A}, i = 1,2,3 a basis for P,(K).
the following expression:
[KJ
,, = ($
+ (dr)r)
Area(K)
Now lengthy but easy computations
i, j = 1,2,3
allow us to get for (3.22)
(3.24)
where
A
d = 12det(A)
ri=x--X
i-1,2,3,
(3.25)
xi = (x:, xi), i = 1,2,3 and X = (X,, X2) are the coordinates of the ith vertex and of the barycenter of K,
respectively. The coefficients of the matrix A = [a,,], I, k = 1,2, are defined as follows. Let us consider
the matrix
[Z,,] = $ x;(x; -X/J , 1, k = 1,2
(3.26)
i=l
we have a,, = l/E I,, + m,212Z22, a12 = uzl = (m,22, - v/E)Z,,, uz2 = l/E I,, + m,,,,Z,,.
Comparing this
new element, called DRT,, with the DRILL element previously introduced we observe that the set of
degrees of freedom defining the DRT, element is the same as in the DRILL element (see Fig. 1).
c. Chinosi et al. I Comput. Methods Appl. Mech. Engrg.
14.3 (1997)
1 -I
Furthermore,
the above considerations
about the construction
of the matrices of the system (3.21) show
that the computational
cost in this operation
is slightly greater than the cost for assembling
the matrix
related to the DRILL element.
4. Numerical
results
In this section we will analyze the convergence
properties
and the performances
of the elements
DRILL and DRT,,. We will use these elements to solve a plain-strain
elasticity problem and we will
compare the results with those obtained solving the same problem with a standard plain-strain
element
[3] with 6 d.o.f. (which we will call PSE6 from now on). We will consider a cantilever beam subjected to
a parabolically
varying end load. Boundary
conditions
are taken in accordance
with an exact solution
(which is known, see [2] pp. 219-220). The geometrical
and the physical data of the problem are shown
in Fig. 2.
In Fig. 3 we will compare the computed vertical tip displacement
(i.e. u2(B)) with the exact solution
as a function of the number of nodes. In Fig. 4 the computed bending stress at point A vs. number of
nodes is shown.
The comparison
with the standard PSE6 element (see Figs. 3 and 4) shows that the DRT,, element
performs better than the DRILL element.
It is known (see [5,7]) that the elements
(like DRILL and
c=2,
Lz
16, P=
I=
-1,
u = 0.3, E = 1, f = 0
h&T, kc) = h&r, fc) = 0,
h(L,
Y> =
0,
h2(L,
Y> =
&
h(O,Y)
= FY,
h2(0,Y)
= -$+
Y El Fig. 2. The cantilever
Y El
-
Y El - Y2),
f$$J]O,c[
beam
0.99
0.97
DRILL --DRTO ---EXSOL. ......-
Fig. 3. Normalized
891
number of nodes
computed
vertical
tip displacement
1261
against
number
x E]O,
L[
c, 4
Y2>,
585.
of nodes.
El- c74
CJ[
C. Chinosi
et al. I Comput.
Methods
Appl.
Mech.
Engrg.
143 (1997)
l-11
-r
0.91
I
1281
0.88
891
number of nodes
585
Fig. 4. Normalized
computed
bending
stress
at the point
A against
DRT,,) obtained from the formulation (2.8) can show a comparatively
effect can be analyzed (see Fig. 5) evaluating the following quantities
SE DRILL =
UyyB)
of nodes
stiff behaviour.
This stiffening
UDRLL(B)
(3.27)
U;SEh(B)
SE RT,, _-
number
uISE6(B) - upRT"(B)
u;~~~(B)
(3.28)
'
as functions of the number of the nodes of the mesh. As one can see the results in Fig. 5 agree with the
0.008
0.007
0.008
ca
0.004
0.003
0.002
0.001
\
0
----------mm_________-___-____--_-.
400
800
number
Fig. 5. Stiffening
effect
against
800
of nodes
number
1000
1200
of nodes.
C. Chinosi PI al. i Cotnput.Mcthdc
10
Appl. Mech. Engrg. 14.1 (1997) 1 -II
-1
-1.5
-2
8
Y
-2.5
B
-3
-3.5
-4
0.5
1.5
log(l/h)
Fig. 6. Relative
displacement
terror 111log-log
scale against
I lh.
ones of Fig. 3; moreover Fig. 5 shows that the good performance
of the DRT,, element is related to a
substantial
reduction
of the stiffening effect.
Now. we define the relative displacement
error E,, and the relative rotation error E, as follows:
(3.29)
(3.30)
where P,. i = 1,
, N are the nodes of the triangulation.
In Figs. 6 and 7 we present in a log-log scale the behaviour of both E, and E, as a function
the slope of the triangle denotes, in each figure the theoretical
rate of convergence.
of 1 /h:
5. Conclusions
We have described and implemented
a new finite element scheme with drilling degrees of freedom.
As far as the convergence
is concerned
the numerical results (see Figs. 6 and 7) show that the elements
with drilling degrees of freedom and the standard
elasticity element
are equivalent
and the results
obtained correspond
to the theoretical
predictions.
As far as the stiff behaviour
is concerned
numerical
experiments
show (see Fig. 5) that the DRT,, element produces a reduction
of the stiffening
effect.
Considering
that DRILL and DRT,, are defined on the same set of degrees of freedom and that their
computational
cost is almost equivalent.
the DRT,, element could be preferable.
As a final remark we
would like to underline.
that drill-elements
can be very effective when applied to the solution of shell
problems:
in this case the shell element is obtained
combining
a plate bending element with a drill
element (used as membrane
element (see [3])).
C. Chinosi et al.
11
I Comput. Methods Appl. Mech. Engrg. 143 (1997) 1-11
-0.5
I
_-
-1
-1.5
___...._._.....:
-2
6
-2.5
2
-3
-3.5
-4
-4.5
-1
-0.5
Fig. 7. Relative
rotation
error
in log-log
scale against
1.5
l/h
References
[l] K.J. Bathe, Finite Element Procedures
in Engineering
Analysis (Prentice-Hall,
Englewood
Cliffs, NJ, 1982).
[2] T.J.R. Hughes. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis (Prentice-Hall,
Englewood
Cliffs, NJ, 1987).
(31 O.C. Zienkiewicz,
The Finite Element Method in Engineering
Science (McGraw-Hill,
London,
1971).
[4] A. Cazzani and S.N. Atluri, Four-noded
mixed finite elements, using unsymmetric
stresses for linear analysis of membranes,
Comput.
Mech. 11 (1993) 229-2.51.
[5] T.J.R. Hughes and F. Brezzi, On drilling degrees of freedom,
Comput.
Methods Appl. Mech. Engrg. 72 (1989) 105-121.
[6] M. Iura and S.N. Atluri. Formulation
of a membrane
finite element with drilling degrees of freedom,
Comput.
Mech. 9
(1992) 417-428.
[7] T.J.R. Hughes, F. Brezzi. A. Masud and I. Harari, Finite elements with drilling degrees of freedom:
theory and numerical
evaluations,
in: R. Gruber, J. Periaux and R.P. Shaw, eds., Proceedings
of the Fifth International
Symposium
on Numerical
Methods in Engineering,
Vol. 1 (Springer Verlag, Berlin, 1990) 3-17.
[8] P.A. Raviart and J.M. Thomas, A mixed finite element method for 2nd order elliptic problems,
in: Mathematical
Aspects of
the Finite Element Method, Lectures Notes in Mathematics
606 (1977) 292-315.
[9] P.G. Ciarlet. The Finite Element Method for Elliptic Problems (North-Holland,
New York, 1978).
Das könnte Ihnen auch gefallen
- Difference Equations in Normed Spaces: Stability and OscillationsVon EverandDifference Equations in Normed Spaces: Stability and OscillationsNoch keine Bewertungen
- Reduction of Finite Element Models of Complex Mechanical ComponentsDokument5 SeitenReduction of Finite Element Models of Complex Mechanical ComponentsAnonymous lEBdswQXmxNoch keine Bewertungen
- Standard-Slope Integration: A New Approach to Numerical IntegrationVon EverandStandard-Slope Integration: A New Approach to Numerical IntegrationNoch keine Bewertungen
- BEMpdfDokument16 SeitenBEMpdfAaditya VikramNoch keine Bewertungen
- 1998 Investigationo F Stressesa T The Fixed End of Deep Cantilever BeamDokument10 Seiten1998 Investigationo F Stressesa T The Fixed End of Deep Cantilever BeamFABIANCHO2210Noch keine Bewertungen
- Blow-up Theory for Elliptic PDEs in Riemannian Geometry (MN-45)Von EverandBlow-up Theory for Elliptic PDEs in Riemannian Geometry (MN-45)Noch keine Bewertungen
- 2order D CorrectedDokument32 Seiten2order D CorrectedslirpaNoch keine Bewertungen
- A Fully Locking Free Isogeometric Approach For Plane Linear Elasticity Problems A Stream Function FormulationDokument13 SeitenA Fully Locking Free Isogeometric Approach For Plane Linear Elasticity Problems A Stream Function FormulationMojtaba MohebiniaNoch keine Bewertungen
- 2 Assumed Stress Membranes With Drilling D.o.f.: 2.1.1 Summary of Recent ResearchDokument19 Seiten2 Assumed Stress Membranes With Drilling D.o.f.: 2.1.1 Summary of Recent ResearchJorge HenriqueNoch keine Bewertungen
- Variational Methods for Boundary Value Problems for Systems of Elliptic EquationsVon EverandVariational Methods for Boundary Value Problems for Systems of Elliptic EquationsNoch keine Bewertungen
- Tensor, Stress, and Strain: Transformation of Vectors and Tensors in Cartesian Coord I N A Te SystemsDokument27 SeitenTensor, Stress, and Strain: Transformation of Vectors and Tensors in Cartesian Coord I N A Te SystemsCaroVallejosNoch keine Bewertungen
- Closed-Form SolutionsDokument13 SeitenClosed-Form SolutionsBza ZaBugNoch keine Bewertungen
- Checkerboard Instabilities in Topological Shape Optimization AlgorithmsDokument5 SeitenCheckerboard Instabilities in Topological Shape Optimization Algorithmsvishal kumar sinhaNoch keine Bewertungen
- MIT3 11F99 AiryDokument14 SeitenMIT3 11F99 AiryADITYANoch keine Bewertungen
- Chapitre 2 PDFDokument17 SeitenChapitre 2 PDFMouhaNoch keine Bewertungen
- Phan-Thien Et Al - 1992 - Completed Double Layer in Half-SpaceDokument15 SeitenPhan-Thien Et Al - 1992 - Completed Double Layer in Half-Spacezihou.liuNoch keine Bewertungen
- Analysis and Approximation of A Vorticity-Velocity-Pressure Formulation For The Oseen EquationsDokument30 SeitenAnalysis and Approximation of A Vorticity-Velocity-Pressure Formulation For The Oseen EquationsYuliza Carolina Capuñay SiesquénNoch keine Bewertungen
- Reissner - 1976 Thick PlatesDokument5 SeitenReissner - 1976 Thick PlatesIoannisPerseusAntypasNoch keine Bewertungen
- Pre Stressed Modal Analysis Using FiniteDokument8 SeitenPre Stressed Modal Analysis Using Finitegreat2008Noch keine Bewertungen
- A Simple Error Estimator and Adaptive Procedure For Practical Engineering AnalysisDokument21 SeitenA Simple Error Estimator and Adaptive Procedure For Practical Engineering AnalysisChao Zhang100% (1)
- Numerical Technique in Plasticity Including Solution Advancement ControlDokument20 SeitenNumerical Technique in Plasticity Including Solution Advancement ControlSebastiao SilvaNoch keine Bewertungen
- Assignment On Metal FormingDokument11 SeitenAssignment On Metal Formingladi11bawaNoch keine Bewertungen
- Bem Project Must UseDokument22 SeitenBem Project Must UseFemi Richard FakoyaNoch keine Bewertungen
- 2D Lid Diven Cavity Final Report PDFDokument24 Seiten2D Lid Diven Cavity Final Report PDFVivek JoshiNoch keine Bewertungen
- STIFFNESSDokument12 SeitenSTIFFNESSMc AsanteNoch keine Bewertungen
- Air Bearing CalculationDokument47 SeitenAir Bearing CalculationtomekzawistowskiNoch keine Bewertungen
- Goal-Oriented Error Control of The Iterative Solution of Finite Element EquationsDokument31 SeitenGoal-Oriented Error Control of The Iterative Solution of Finite Element EquationsOsman HusseinNoch keine Bewertungen
- Wave Equation Applications in Peridynamic Model: Hisham M. Ali HasanDokument5 SeitenWave Equation Applications in Peridynamic Model: Hisham M. Ali Hasansar0000Noch keine Bewertungen
- A Mixed-Enhanced Formulation For Tetrahedral Finite ElementsDokument24 SeitenA Mixed-Enhanced Formulation For Tetrahedral Finite ElementsAlfito Januar HNoch keine Bewertungen
- Torsion of Orthotropic Bars With L-Shaped or Cruciform Cross-SectionDokument15 SeitenTorsion of Orthotropic Bars With L-Shaped or Cruciform Cross-SectionRaquel CarmonaNoch keine Bewertungen
- Maxwell ModelDokument20 SeitenMaxwell ModelJasleen Kaur HoraNoch keine Bewertungen
- Mindlin Eshel 1968Dokument16 SeitenMindlin Eshel 1968Don't BeCuriousNoch keine Bewertungen
- Adjoint of A Median-Dual Finite-Volume Scheme Application To Transonic Aerodynamic Shape OptimizationDokument39 SeitenAdjoint of A Median-Dual Finite-Volume Scheme Application To Transonic Aerodynamic Shape OptimizationOlivier AmoignonNoch keine Bewertungen
- Matriz de Rigidez GeometricaDokument14 SeitenMatriz de Rigidez GeometricaManuel CruzNoch keine Bewertungen
- Smtdia B R R R, Albuquerque, New Mexico 87115, U.S.ADokument14 SeitenSmtdia B R R R, Albuquerque, New Mexico 87115, U.S.ANilthson Noreña ValverdeNoch keine Bewertungen
- Collapse Load Analysis of Yield-Line ElementsDokument7 SeitenCollapse Load Analysis of Yield-Line ElementsAlaa Elsisi100% (1)
- Paper#1155 Final RevisionDokument25 SeitenPaper#1155 Final RevisioncyrusnasiraiNoch keine Bewertungen
- Shear Correction Factors in Timoshenko's Beam Theory For Arbitrary Shaped Cross-SectionsDokument9 SeitenShear Correction Factors in Timoshenko's Beam Theory For Arbitrary Shaped Cross-SectionsXuejian LiuNoch keine Bewertungen
- Capurso - Limit Analysis of Continuous Media With Piecewise Linear Yield ConditionDokument6 SeitenCapurso - Limit Analysis of Continuous Media With Piecewise Linear Yield ConditionDebasisMohapatraNoch keine Bewertungen
- Introduction To Finite Element AnalysisDokument20 SeitenIntroduction To Finite Element AnalysisVishnu Vardhan Reddy GangapuramNoch keine Bewertungen
- Chapter - 8 Master Dynamic Stability Formula For Structural Members Subjected To Periodic LoadsDokument14 SeitenChapter - 8 Master Dynamic Stability Formula For Structural Members Subjected To Periodic LoadsSumanth BhavanasiNoch keine Bewertungen
- Appendix: Analytical DynamicsDokument7 SeitenAppendix: Analytical DynamicsLeandro LandgrafNoch keine Bewertungen
- S MM R C S e SDokument22 SeitenS MM R C S e Ssmanoj354Noch keine Bewertungen
- Finite Element Technology: Lecture NotesDokument63 SeitenFinite Element Technology: Lecture NotesJuan Francisco Acuña ContrerasNoch keine Bewertungen
- Finite Element Formulations: U U ,) D V U ,) V 0Dokument8 SeitenFinite Element Formulations: U U ,) D V U ,) V 0aman maharNoch keine Bewertungen
- Westergaard Stress Functions For Displacement-Prescribed Crack - TadaDokument15 SeitenWestergaard Stress Functions For Displacement-Prescribed Crack - TadaMarilene LobatoNoch keine Bewertungen
- BEM of Viscoelatic ModelDokument8 SeitenBEM of Viscoelatic ModelFemi Richard FakoyaNoch keine Bewertungen
- Chapter 16Dokument43 SeitenChapter 16German ToledoNoch keine Bewertungen
- Solution Manual For Aerodynamics For Engineering Students 6th Edition Houghton Carpenter Collicott Valentine 0080966322 9780080966328Dokument42 SeitenSolution Manual For Aerodynamics For Engineering Students 6th Edition Houghton Carpenter Collicott Valentine 0080966322 9780080966328steven.edwards412100% (15)
- Aerodynamics For Engineering Students 6th Edition Houghton Carpenter Collicott Valentine Solution ManualDokument11 SeitenAerodynamics For Engineering Students 6th Edition Houghton Carpenter Collicott Valentine Solution Manualchristopher100% (25)
- Key Words and PhrasesDokument17 SeitenKey Words and PhrasesOscar Ivan Londoño GalvizNoch keine Bewertungen
- Wilson 1990Dokument13 SeitenWilson 1990Sebastiao SilvaNoch keine Bewertungen
- Plane Stress and Plane Strain: 4.2.1 Displacement FunctionsDokument25 SeitenPlane Stress and Plane Strain: 4.2.1 Displacement FunctionswearplayNoch keine Bewertungen
- Minimization Approach To Limit Solutions of Plates: The University of Michigan, Ann Arbor, MI 48109, USADokument10 SeitenMinimization Approach To Limit Solutions of Plates: The University of Michigan, Ann Arbor, MI 48109, USAfefahimNoch keine Bewertungen
- Green's Theorem and Isolation in Planar Graphs: Raghunath Tewari N. V. Vinodchandran September 30, 2010Dokument10 SeitenGreen's Theorem and Isolation in Planar Graphs: Raghunath Tewari N. V. Vinodchandran September 30, 2010carlosandres2040Noch keine Bewertungen
- CH 07Dokument77 SeitenCH 07LeonardoMadeira11Noch keine Bewertungen
- Chapter 06bDokument17 SeitenChapter 06bgioNoch keine Bewertungen
- Tensor Voting: Theory and Applications: Gérard Medioni Chi-Keung Tang Mi-Suen LeeDokument10 SeitenTensor Voting: Theory and Applications: Gérard Medioni Chi-Keung Tang Mi-Suen LeeM Rameez Ur RehmanNoch keine Bewertungen
- List of Math SymbolsDokument11 SeitenList of Math SymbolsAlaa' MowafiNoch keine Bewertungen
- N-Dimensional Rotation Matrix Generation Algorithm: March 2018Dokument8 SeitenN-Dimensional Rotation Matrix Generation Algorithm: March 2018Yasser NaguibNoch keine Bewertungen
- Computer Vision: Mubarak Shah Computer Vision Lab University of Central Florida Orlando, FL 32816Dokument24 SeitenComputer Vision: Mubarak Shah Computer Vision Lab University of Central Florida Orlando, FL 32816mayilsamythangarajuNoch keine Bewertungen
- (Baker A.) Representations of Finite Groups (BookFi)Dokument80 Seiten(Baker A.) Representations of Finite Groups (BookFi)mastermathNoch keine Bewertungen
- Mechatronics SyllabusDokument142 SeitenMechatronics SyllabustejassidhpuraNoch keine Bewertungen
- Mechanical EngineeringDokument135 SeitenMechanical EngineeringjitenderNoch keine Bewertungen
- Design of Experiments: There Are Many Books That Address Experimental Design and Present FactoDokument33 SeitenDesign of Experiments: There Are Many Books That Address Experimental Design and Present Factorarunr1Noch keine Bewertungen
- M. Sc. Tech. Indus. MathsDokument135 SeitenM. Sc. Tech. Indus. MathsrapsjadeNoch keine Bewertungen
- 2005 Q 0035 Postulates of Quantum MechanicsDokument89 Seiten2005 Q 0035 Postulates of Quantum MechanicsMd Delowar Hossain MithuNoch keine Bewertungen
- TARAY - Laboratory Experiment 7 Matrix AnalysisDokument8 SeitenTARAY - Laboratory Experiment 7 Matrix AnalysisFEOLO RIEL BENITEZ TARAYNoch keine Bewertungen
- Electronics and CommunicationsDokument4 SeitenElectronics and CommunicationsPranav AsthanaNoch keine Bewertungen
- Linear Algebra Inner ProductDokument3 SeitenLinear Algebra Inner ProductkamleshNoch keine Bewertungen
- Chemistry Books: S.No Authors /publisher Name of Books RemarksDokument16 SeitenChemistry Books: S.No Authors /publisher Name of Books RemarksKunwar Vashistha Narayan TyagiNoch keine Bewertungen
- History of VectorsDokument4 SeitenHistory of VectorsCAROL_X1Noch keine Bewertungen
- Prepared by Ladybird: Topics Year (No. of Question in Exam) 2007 2008 2009 Form 4Dokument2 SeitenPrepared by Ladybird: Topics Year (No. of Question in Exam) 2007 2008 2009 Form 4sewcinNoch keine Bewertungen
- Group 3 - Review Buku Geometri (Inggris)Dokument247 SeitenGroup 3 - Review Buku Geometri (Inggris)Grace Margareth Stevany SinuratNoch keine Bewertungen
- Maa6617 Course Notes SPRING 2020Dokument51 SeitenMaa6617 Course Notes SPRING 2020EDU CIPANANoch keine Bewertungen
- Digital Communications (EECS-4214) : (Fall-2021)Dokument24 SeitenDigital Communications (EECS-4214) : (Fall-2021)Samyak JainNoch keine Bewertungen
- Professional Linear Algebra Assignment HelpDokument3 SeitenProfessional Linear Algebra Assignment HelpMath Homework SolverNoch keine Bewertungen
- Grade 12 AS Sir Lecture DetailsDokument21 SeitenGrade 12 AS Sir Lecture DetailsManthan HaritashNoch keine Bewertungen
- Tshri Vile Parle Kelvani Mandal'S D. J. Sanghvi College of Engineering Department of Information Technology Semester: Iii Subject: Java Programming LabDokument11 SeitenTshri Vile Parle Kelvani Mandal'S D. J. Sanghvi College of Engineering Department of Information Technology Semester: Iii Subject: Java Programming Labsnehal patilNoch keine Bewertungen
- Linear Network Error Correction Coding (Xuan Guang Zhen Zhang)Dokument110 SeitenLinear Network Error Correction Coding (Xuan Guang Zhen Zhang)Anonymous bZtJlFvPtpNoch keine Bewertungen
- B.Tech MME Syllabus PDFDokument201 SeitenB.Tech MME Syllabus PDFPreetiNoch keine Bewertungen
- Vectors Tensors CompleteDokument206 SeitenVectors Tensors CompleteSukrit GhoraiNoch keine Bewertungen
- Symmetry Relationships Between Crystal StructuresDokument349 SeitenSymmetry Relationships Between Crystal StructuresRocio Iribarren VargasNoch keine Bewertungen
- General Form For LMP PDFDokument11 SeitenGeneral Form For LMP PDFsaraswatthiNoch keine Bewertungen
- MCA Syallabus PDFDokument136 SeitenMCA Syallabus PDFjoby georgeNoch keine Bewertungen
- Feature Extraction With Geometric Algebra For Semi - Supervised Learning of Time-Series Spatial VectorDokument4 SeitenFeature Extraction With Geometric Algebra For Semi - Supervised Learning of Time-Series Spatial Vectorkurisu_jpNoch keine Bewertungen
- An Introduction To Frames and Riesz Bases (PDFDrive) PDFDokument449 SeitenAn Introduction To Frames and Riesz Bases (PDFDrive) PDFRosana Radović100% (1)
- Mental Math: How to Develop a Mind for Numbers, Rapid Calculations and Creative Math Tricks (Including Special Speed Math for SAT, GMAT and GRE Students)Von EverandMental Math: How to Develop a Mind for Numbers, Rapid Calculations and Creative Math Tricks (Including Special Speed Math for SAT, GMAT and GRE Students)Noch keine Bewertungen
- Quantum Physics: A Beginners Guide to How Quantum Physics Affects Everything around UsVon EverandQuantum Physics: A Beginners Guide to How Quantum Physics Affects Everything around UsBewertung: 4.5 von 5 Sternen4.5/5 (3)
- Images of Mathematics Viewed Through Number, Algebra, and GeometryVon EverandImages of Mathematics Viewed Through Number, Algebra, and GeometryNoch keine Bewertungen
- Basic Math & Pre-Algebra Workbook For Dummies with Online PracticeVon EverandBasic Math & Pre-Algebra Workbook For Dummies with Online PracticeBewertung: 4 von 5 Sternen4/5 (2)
- Build a Mathematical Mind - Even If You Think You Can't Have One: Become a Pattern Detective. Boost Your Critical and Logical Thinking Skills.Von EverandBuild a Mathematical Mind - Even If You Think You Can't Have One: Become a Pattern Detective. Boost Your Critical and Logical Thinking Skills.Bewertung: 5 von 5 Sternen5/5 (1)
- A Mathematician's Lament: How School Cheats Us Out of Our Most Fascinating and Imaginative Art FormVon EverandA Mathematician's Lament: How School Cheats Us Out of Our Most Fascinating and Imaginative Art FormBewertung: 5 von 5 Sternen5/5 (5)
- Math Workshop, Grade K: A Framework for Guided Math and Independent PracticeVon EverandMath Workshop, Grade K: A Framework for Guided Math and Independent PracticeBewertung: 5 von 5 Sternen5/5 (1)
- Limitless Mind: Learn, Lead, and Live Without BarriersVon EverandLimitless Mind: Learn, Lead, and Live Without BarriersBewertung: 4 von 5 Sternen4/5 (6)
- Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative TeachingVon EverandMathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative TeachingBewertung: 4.5 von 5 Sternen4.5/5 (21)
- A Guide to Success with Math: An Interactive Approach to Understanding and Teaching Orton Gillingham MathVon EverandA Guide to Success with Math: An Interactive Approach to Understanding and Teaching Orton Gillingham MathBewertung: 5 von 5 Sternen5/5 (1)