Beruflich Dokumente
Kultur Dokumente
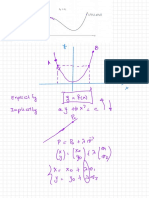
Arc-Length Parameterization: R (T) Rcos I + Rsin J + T K, 0 T H
Hochgeladen von
mangalvao2009Originalbeschreibung:
Originaltitel
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Arc-Length Parameterization: R (T) Rcos I + Rsin J + T K, 0 T H
Hochgeladen von
mangalvao2009Copyright:
Verfügbare Formate
Chapter 3 | Vector-Valued Functions 285
⎛ ⎞ ⎛ ⎞
r(t) = Rcos⎝2πNt ⎠ i + Rsin⎝2πNt ⎠ j + t k, 0 ≤ t ≤ h,
h h
where R represents the radius of the helix, h represents the height (distance between two consecutive turns), and the helix
completes N turns. Let’s derive a formula for the arc length of this helix using Equation 3.12. First of all,
⎛ ⎞ ⎛ ⎞
r′(t) = − 2πNR sin⎝2πNt ⎠ i + 2πNR cos⎝2πNt ⎠ j + k.
h h h h
Therefore,
b
s = ∫ ‖ r′(t) ‖ dt
a
⎛ 2πNR ⎛2πNt ⎞⎞ ⎛2πNR ⎛2πNt ⎞⎞
h 2 2
=∫ 2
⎝− h sin⎝ h ⎠⎠ + ⎝ h cos⎝ h ⎠⎠ + 1 dt
0
4π 2 N 2 R 2 ⎛sin 2 ⎛2πNt ⎞ + cos 2 ⎛2πNt ⎞⎞ + 1dt
h
=∫ ⎝ ⎝ h ⎠ ⎝ h ⎠⎠
0 h2
h
=∫ 4π 2 N 2 R 2 + 1dt
0 h2
⎡ 2 2 2 ⎤h
= ⎢ t 4π N2 R + 1⎥ 0
⎣ h ⎦
2 2 2 2
= h 4π N R2 + h
h
= 4π 2 N 2 R 2 + h 2.
This gives a formula for the length of a wire needed to form a helix with N turns that has radius R and height h.
Arc-Length Parameterization
We now have a formula for the arc length of a curve defined by a vector-valued function. Let’s take this one step further
and examine what an arc-length function is.
If a vector-valued function represents the position of a particle in space as a function of time, then the arc-length function
measures how far that particle travels as a function of time. The formula for the arc-length function follows directly from
the formula for arc length:
t (3.13)
s(t) = ∫ ⎛
⎝ f ′ (u)⎞⎠ 2 + ⎛⎝g′ (u)⎞⎠ 2 + ⎛⎝h′ (u)⎞⎠ 2du.
a
If the curve is in two dimensions, then only two terms appear under the square root inside the integral. The reason for using
the independent variable u is to distinguish between time and the variable of integration. Since s(t) measures distance
traveled as a function of time, s′ (t) measures the speed of the particle at any given time. Since we have a formula for s(t)
in Equation 3.13, we can differentiate both sides of the equation:
⎡ t ⎤
s′ (t) = d ∫ ⎛⎝ f ′ (u)⎞⎠ 2 + ⎛⎝g′ (u)⎞⎠ 2 + ⎛⎝h′ (u)⎞⎠ 2du
dt ⎣ a ⎦
⎡ t ⎤
= d ∫ ‖ r′(u) ‖ du
dt ⎣ a ⎦
= ‖ r′(t) ‖ .
If we assume that r(t) defines a smooth curve, then the arc length is always increasing, so s′ (t) > 0 for t > a. Last, if
r(t) is a curve on which ‖ r′(t) ‖ = 1 for all t, then
t t
s(t) = ∫ ‖ r′(u) ‖ du = ∫ 1 du = t − a,
a a
which means that t represents the arc length as long as a = 0.
Das könnte Ihnen auch gefallen
- Marxism and The Oppression of Women Lise VogelDokument259 SeitenMarxism and The Oppression of Women Lise VogelMoises SaavedraNoch keine Bewertungen
- MA2104 Midterm 18/19Dokument13 SeitenMA2104 Midterm 18/19Robert Fisher100% (1)
- Frequency Converter English ManualDokument33 SeitenFrequency Converter English Manualproduccion multipack100% (2)
- JDM B18C Type RDokument6 SeitenJDM B18C Type RSeenka CapuqNoch keine Bewertungen
- SIM1003 Chapter 12 NotesDokument5 SeitenSIM1003 Chapter 12 NotesMin Hui LeeNoch keine Bewertungen
- 12.3 Curvature, Torsion and The TNB Frame: DT DsDokument18 Seiten12.3 Curvature, Torsion and The TNB Frame: DT DsMilad RadNoch keine Bewertungen
- Space Curves 1Dokument12 SeitenSpace Curves 1John KimaniNoch keine Bewertungen
- MA3D9 Example Sheet 1Dokument4 SeitenMA3D9 Example Sheet 1Abraham HernandezNoch keine Bewertungen
- Q QV QR W MDokument4 SeitenQ QV QR W Mjrobs314Noch keine Bewertungen
- ES2A7 - Fluid Mechanics Example Classes Example Questions (Set IV)Dokument8 SeitenES2A7 - Fluid Mechanics Example Classes Example Questions (Set IV)Alejandro PerezNoch keine Bewertungen
- ENG 233 Lecture Notes 3Dokument5 SeitenENG 233 Lecture Notes 3David Mitry ThomasNoch keine Bewertungen
- Vector FunctionsDokument93 SeitenVector FunctionsResty BalinasNoch keine Bewertungen
- D G Chapter 3Dokument13 SeitenD G Chapter 3Tayyaba AfzalNoch keine Bewertungen
- Application of Calculus, B.SC, Notes On Arc LengthDokument4 SeitenApplication of Calculus, B.SC, Notes On Arc Lengthkishalay sarkarNoch keine Bewertungen
- VelocityDokument16 SeitenVelocityhimanshu10092004Noch keine Bewertungen
- Differential and Integral Calculus 2 - Homework 2 SolutionDokument5 SeitenDifferential and Integral Calculus 2 - Homework 2 SolutionDominikNoch keine Bewertungen
- Parametric Path: Paths and Curves in RDokument3 SeitenParametric Path: Paths and Curves in RRajNoch keine Bewertungen
- Appendix PDFDokument51 SeitenAppendix PDFAnonymous Gd16J3n7Noch keine Bewertungen
- Vector Valued FunctionDokument33 SeitenVector Valued FunctionFarhan naseenNoch keine Bewertungen
- Chapter 2. Parameterized Curves in RDokument25 SeitenChapter 2. Parameterized Curves in RAdelin VătăşescuNoch keine Bewertungen
- Revised Assignment CycloidDokument7 SeitenRevised Assignment Cycloidaneeqa.shahzadNoch keine Bewertungen
- Week 2: Elementary Calculus of Vector Functions and CurvesDokument10 SeitenWeek 2: Elementary Calculus of Vector Functions and CurvesTeresa Villena GonzálezNoch keine Bewertungen
- 6-Integration of Vector-Valued Functions, Arc LengthDokument5 Seiten6-Integration of Vector-Valued Functions, Arc LengthslowjamsNoch keine Bewertungen
- Section 13.2 Derivatives and Integrals of Vector FunctionsDokument3 SeitenSection 13.2 Derivatives and Integrals of Vector FunctionsAlvin AdityaNoch keine Bewertungen
- Multivariable and Vector Analysis: WwlchenDokument8 SeitenMultivariable and Vector Analysis: WwlchenMay D. CahyaNoch keine Bewertungen
- Oscillation of Second Order Nonlinear Neutral Differential Equations With Mixed Neutral TermDokument10 SeitenOscillation of Second Order Nonlinear Neutral Differential Equations With Mixed Neutral TermRobin Achmad KurenaiNoch keine Bewertungen
- sm2 052 PDFDokument4 Seitensm2 052 PDFNilton MafraNoch keine Bewertungen
- Brachistochrone Problem and It's Real-Life Application On ArchitectureDokument19 SeitenBrachistochrone Problem and It's Real-Life Application On ArchitectureKhola KhanNoch keine Bewertungen
- Calculus 3Dokument2 SeitenCalculus 3simbachipsyNoch keine Bewertungen
- Difference Between Social and Natural ScienceDokument5 SeitenDifference Between Social and Natural ScienceBilal Ahmad AliNoch keine Bewertungen
- Related RateDokument1 SeiteRelated RateJOHN MICHAEL ARMENTANoch keine Bewertungen
- Week 11 L1Dokument8 SeitenWeek 11 L1Venkat ReddiNoch keine Bewertungen
- Differential Geometry of Curves and Surfaces by Manfredo Perdigão Do Carmo Homework3Dokument2 SeitenDifferential Geometry of Curves and Surfaces by Manfredo Perdigão Do Carmo Homework3publicacc71Noch keine Bewertungen
- 2016 - Bourquard - CAPS Technical Note On Acoustic MeasurementsDokument26 Seiten2016 - Bourquard - CAPS Technical Note On Acoustic MeasurementslakaviyNoch keine Bewertungen
- Chapter 13 PDFDokument74 SeitenChapter 13 PDFSiddharth GandhiNoch keine Bewertungen
- Signals Approximation, 2 NfcietDokument7 SeitenSignals Approximation, 2 Nfcietapi-19788618Noch keine Bewertungen
- Appendix A. The DQ TransformationDokument8 SeitenAppendix A. The DQ TransformationtiagokjNoch keine Bewertungen
- 3 Heat Equations and Maximum PrinciplesDokument4 Seiten3 Heat Equations and Maximum PrinciplesAbdelaliElFaizNoch keine Bewertungen
- Poincaré MetricDokument24 SeitenPoincaré MetricRohan RajagopalNoch keine Bewertungen
- 1 XXX 2 XXX 3 Laplace'S Equation in Cylindrical Po-Lar CoordinatesDokument3 Seiten1 XXX 2 XXX 3 Laplace'S Equation in Cylindrical Po-Lar CoordinatesGovanna StarNoch keine Bewertungen
- 502.gaussian GeometryDokument71 Seiten502.gaussian GeometrycarlomettaNoch keine Bewertungen
- Exersice Set2 2024Dokument3 SeitenExersice Set2 2024Ayoub GHOULNoch keine Bewertungen
- Vector-Valued FunctionsDokument21 SeitenVector-Valued Functionspapu corelNoch keine Bewertungen
- Unit-4, Vector Differential CalculusDokument31 SeitenUnit-4, Vector Differential CalculusSujatha VivekNoch keine Bewertungen
- Section10 4notes PDFDokument10 SeitenSection10 4notes PDFjerald vernon torresNoch keine Bewertungen
- Arc Length and Surface Area in Parametric Equations: MATH 211, Calculus IIDokument27 SeitenArc Length and Surface Area in Parametric Equations: MATH 211, Calculus IIAli ElbasryNoch keine Bewertungen
- Vector Valued FunctionsDokument75 SeitenVector Valued Functionsfarwa jabinNoch keine Bewertungen
- Pendulum PDFDokument8 SeitenPendulum PDFMohammad AhmerNoch keine Bewertungen
- EEE 303 HW # 1 SolutionsDokument22 SeitenEEE 303 HW # 1 SolutionsDhirendra Kumar SinghNoch keine Bewertungen
- MATH 115: Lecture IX NotesDokument2 SeitenMATH 115: Lecture IX NotesDylan C. BeckNoch keine Bewertungen
- Lecture - 36: Wave Propagation in Continuum SystemDokument4 SeitenLecture - 36: Wave Propagation in Continuum SystemgauthamNoch keine Bewertungen
- 2010 Fall With SolutionsDokument36 Seiten2010 Fall With SolutionsRay MondoNoch keine Bewertungen
- NOTES - Conics, Parametric Equations, and Polar Coordinates (CHPT 10)Dokument6 SeitenNOTES - Conics, Parametric Equations, and Polar Coordinates (CHPT 10)nyan kumamonNoch keine Bewertungen
- Power Spectral DensityDokument5 SeitenPower Spectral DensityJasper JamirNoch keine Bewertungen
- Answers To Assignment 5 Continuity, Bernouilli and Energy EquationDokument4 SeitenAnswers To Assignment 5 Continuity, Bernouilli and Energy EquationAbhinandan RamkrishnanNoch keine Bewertungen
- S2 Mathematics Module 1 HandoutDokument32 SeitenS2 Mathematics Module 1 HandoutAakanksha KartikNoch keine Bewertungen
- Derivations NIP Course: 1 Encoding LecturesDokument7 SeitenDerivations NIP Course: 1 Encoding LecturesMuhammad NoerrahmanNoch keine Bewertungen
- ملخص لشابتر9.5 to 9.9 PDFDokument13 Seitenملخص لشابتر9.5 to 9.9 PDFBalqees AlriyamiNoch keine Bewertungen
- 13 Electric Motor HandbookDokument317 Seiten13 Electric Motor HandbookWâhýûðî Fãjâr67% (3)
- Chapter02 03 SJDokument5 SeitenChapter02 03 SJkaviNoch keine Bewertungen
- FluidmechanicsDokument62 SeitenFluidmechanicsNadiaa AdjoviNoch keine Bewertungen
- The Spectral Theory of Toeplitz Operators. (AM-99), Volume 99Von EverandThe Spectral Theory of Toeplitz Operators. (AM-99), Volume 99Noch keine Bewertungen
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)Von EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)Noch keine Bewertungen
- Different 300 1830. 1552,: Structure of The Quantum WorldDokument1 SeiteDifferent 300 1830. 1552,: Structure of The Quantum Worldmangalvao2009Noch keine Bewertungen
- Mixer: ToolbarDokument1 SeiteMixer: Toolbarmangalvao2009Noch keine Bewertungen
- NalgDokument1 SeiteNalgmangalvao2009Noch keine Bewertungen
- (1989), Three 1967, 1 1966. 1983, (1983) .) 5: 5 - 5 Quantum Theory's Bedrock: A History ExtraordinaryDokument1 Seite(1989), Three 1967, 1 1966. 1983, (1983) .) 5: 5 - 5 Quantum Theory's Bedrock: A History Extraordinarymangalvao2009Noch keine Bewertungen
- Structure of The Quantum World 25 1Dokument1 SeiteStructure of The Quantum World 25 1mangalvao2009Noch keine Bewertungen
- The Media Pool: The Cut Page Default Workspace, With The Media Pool in Icon ViewDokument1 SeiteThe Media Pool: The Cut Page Default Workspace, With The Media Pool in Icon Viewmangalvao2009Noch keine Bewertungen
- 5 .9 Solution of The Elitzur-Vaidman Bomb-Testing ProblemDokument1 Seite5 .9 Solution of The Elitzur-Vaidman Bomb-Testing Problemmangalvao2009Noch keine Bewertungen
- 238 Structure of The Quantum WorldDokument1 Seite238 Structure of The Quantum Worldmangalvao2009Noch keine Bewertungen
- Entangled: Structure of The Quantum WorldDokument1 SeiteEntangled: Structure of The Quantum Worldmangalvao2009Noch keine Bewertungen
- Quantum Theory and RealityDokument1 SeiteQuantum Theory and Realitymangalvao2009Noch keine Bewertungen
- Tutorial 03: Quest Editor: Creating A New QuestDokument1 SeiteTutorial 03: Quest Editor: Creating A New Questmangalvao2009Noch keine Bewertungen
- Viewer Tabs: Adding Clips To The TimelineDokument1 SeiteViewer Tabs: Adding Clips To The Timelinemangalvao2009Noch keine Bewertungen
- The Work Area: The Work Area Showing The Node Editor, The Spline Editor, and Keyframes EditorDokument1 SeiteThe Work Area: The Work Area Showing The Node Editor, The Spline Editor, and Keyframes Editormangalvao2009Noch keine Bewertungen
- The Media PageDokument1 SeiteThe Media Pagemangalvao2009Noch keine Bewertungen
- Appending Clips Ensures There Are No Gaps Between Them On The TimelineDokument1 SeiteAppending Clips Ensures There Are No Gaps Between Them On The Timelinemangalvao2009Noch keine Bewertungen
- Adjusting The Lift':: Davinci ResolveDokument1 SeiteAdjusting The Lift':: Davinci Resolvemangalvao2009Noch keine Bewertungen
- TyuiDokument1 SeiteTyuimangalvao2009Noch keine Bewertungen
- The Project Manager: Individual Preferences and Settings Based On LoginDokument1 SeiteThe Project Manager: Individual Preferences and Settings Based On Loginmangalvao2009Noch keine Bewertungen
- Updating Pathing and The Map: Default ZoomDokument1 SeiteUpdating Pathing and The Map: Default Zoommangalvao2009Noch keine Bewertungen
- Ÿ D, Ijk Ilmmnoppqrmlstntumv Wxy ZW (Qy U/Zpqn) - 'P) - 'At (/BQRCRJKDokument1 SeiteŸ D, Ijk Ilmmnoppqrmlstntumv Wxy ZW (Qy U/Zpqn) - 'P) - 'At (/BQRCRJKmangalvao2009Noch keine Bewertungen
- Ÿ D, Ijk Ilmmnoppqrmlstntumv Wxy ZW (Qy U/Zpqn) - 'P) - 'At (/BQRCRJKDokument2 SeitenŸ D, Ijk Ilmmnoppqrmlstntumv Wxy ZW (Qy U/Zpqn) - 'P) - 'At (/BQRCRJKmangalvao2009Noch keine Bewertungen
- Páginas de Grim Dawn Modding GuideDokument1 SeitePáginas de Grim Dawn Modding Guidemangalvao2009Noch keine Bewertungen
- Levels of Structural Organization: From Atoms To Organisms PhysiologyDokument1 SeiteLevels of Structural Organization: From Atoms To Organisms Physiologymangalvao2009Noch keine Bewertungen
- Introduction and Overview: "Calculus I" Is Divided Into Five Chapters. Sequences and Series Are Introduced in Chapter 1Dokument1 SeiteIntroduction and Overview: "Calculus I" Is Divided Into Five Chapters. Sequences and Series Are Introduced in Chapter 1mangalvao2009Noch keine Bewertungen
- Vlo PDFDokument1 SeiteVlo PDFmangalvao2009Noch keine Bewertungen
- Resonance Imaging (Mri), Which: Tissues, Such As The Brain or InterverDokument1 SeiteResonance Imaging (Mri), Which: Tissues, Such As The Brain or Intervermangalvao2009Noch keine Bewertungen
- Example 3.9: Finding The Arc LengthDokument1 SeiteExample 3.9: Finding The Arc Lengthmangalvao2009Noch keine Bewertungen
- PligfulDokument1 SeitePligfulmangalvao2009Noch keine Bewertungen
- Ow Fossils Form: Fossilized Hedgehog PholidocercusDokument1 SeiteOw Fossils Form: Fossilized Hedgehog Pholidocercusmangalvao2009Noch keine Bewertungen
- FlibDokument1 SeiteFlibmangalvao2009Noch keine Bewertungen
- Case Study (Co2 Flooding)Dokument10 SeitenCase Study (Co2 Flooding)Jessica KingNoch keine Bewertungen
- Air System Sizing Summary For NIVEL PB - Zona 1Dokument1 SeiteAir System Sizing Summary For NIVEL PB - Zona 1Roger PandoNoch keine Bewertungen
- The Royal Commonwealth Society of Malaysia: Function MenuDokument3 SeitenThe Royal Commonwealth Society of Malaysia: Function MenuMynak KrishnaNoch keine Bewertungen
- EMV Card Reader Upgrade Kit Instructions - 05162016Dokument6 SeitenEMV Card Reader Upgrade Kit Instructions - 05162016Shashi K KumarNoch keine Bewertungen
- Astm D974-97Dokument7 SeitenAstm D974-97QcHeNoch keine Bewertungen
- Feasibility Study On The Seaweed Kappaphycus Alvarezii Cultivation Site in Indari Waters ofDokument9 SeitenFeasibility Study On The Seaweed Kappaphycus Alvarezii Cultivation Site in Indari Waters ofUsman MadubunNoch keine Bewertungen
- AeonDokument4 SeitenAeonsancsa_74Noch keine Bewertungen
- Commercial Kitchen Fire InvestigationsDokument6 SeitenCommercial Kitchen Fire InvestigationsBen ConnonNoch keine Bewertungen
- 02-09-18 SR - IZ Jee-Adv 2011-P1 PTA-03 Q PDFDokument31 Seiten02-09-18 SR - IZ Jee-Adv 2011-P1 PTA-03 Q PDFswarupNoch keine Bewertungen
- 6.003 Homework #12 Solutions: ProblemsDokument9 Seiten6.003 Homework #12 Solutions: ProblemsSamu PacurucuNoch keine Bewertungen
- Need For Advanced Suspension SystemsDokument10 SeitenNeed For Advanced Suspension SystemsIQPC GmbHNoch keine Bewertungen
- Sample Dewa Inspection CommentsDokument2 SeitenSample Dewa Inspection Commentsrmtaqui100% (1)
- Chapter 9 Material ChangesDokument6 SeitenChapter 9 Material ChangesFitria Istikomah DewiNoch keine Bewertungen
- UntitledDokument413 SeitenUntitledjgj38j90Noch keine Bewertungen
- IDRW MagazineDokument10 SeitenIDRW MagazineVirarya100% (1)
- Company Profile Pt. KPT PDFDokument23 SeitenCompany Profile Pt. KPT PDFfery buyaNoch keine Bewertungen
- BCSL 058 Previous Year Question Papers by IgnouassignmentguruDokument45 SeitenBCSL 058 Previous Year Question Papers by IgnouassignmentguruSHIKHA JAINNoch keine Bewertungen
- Thesis Brand BlanketDokument4 SeitenThesis Brand BlanketKayla Smith100% (2)
- Module 02 Connect Hardware Peripherals EndaleDokument49 SeitenModule 02 Connect Hardware Peripherals EndaleSoli Mondo100% (1)
- Practical Considerations in Modeling: Physical Interactions Taking Place Within A BodyDokument35 SeitenPractical Considerations in Modeling: Physical Interactions Taking Place Within A BodyFábio1 GamaNoch keine Bewertungen
- Aesa Based Pechay Production - AbdulwahidDokument17 SeitenAesa Based Pechay Production - AbdulwahidAnne Xx100% (1)
- Technical Design of The Bukwimba Open Pit Final 12042017Dokument31 SeitenTechnical Design of The Bukwimba Open Pit Final 12042017Rozalia PengoNoch keine Bewertungen
- DLL - Mapeh 6 - Q2 - W8Dokument6 SeitenDLL - Mapeh 6 - Q2 - W8Joe Marie FloresNoch keine Bewertungen
- Sandvik Saf 31803 Tube and Pipe, Seamless: DatasheetDokument9 SeitenSandvik Saf 31803 Tube and Pipe, Seamless: DatasheetPaul NeedhamNoch keine Bewertungen
- Farmhouse Style Plans - Farm & CountryDokument6 SeitenFarmhouse Style Plans - Farm & Countryhanif azriNoch keine Bewertungen
- Pertanyaan TK PDBDokument4 SeitenPertanyaan TK PDBHardenNoch keine Bewertungen
- E Numbers Are Number Codes ForDokument3 SeitenE Numbers Are Number Codes ForaradhyaNoch keine Bewertungen