Beruflich Dokumente
Kultur Dokumente
Vaz 2010
Hochgeladen von
Musa MohammadCopyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
Vaz 2010
Hochgeladen von
Musa MohammadCopyright:
Verfügbare Formate
Well Injectivity Decline for
A. S. L. Vaz, Jr.
Nonlinear Filtration of Injected
North Fluminense State University,
Avenida Alberto Lamego 2000,
Campos dos Goytacazes,
Suspension: Semi-Analytical
28013-602 Rio de Janeiro, Brazil
Model
P. Bedrikovetsky
e-mail: pavel@asp.adelaide.edu.au Injectivity decline due to injection of water with particles is a widespread phenomenon in
SPE, waterflood projects. It happens due to particle capture by rocks and consequent perme-
Australian School of Petroleum, ability decline and also due to external cake formation on the sandface. Since offshore
University of Adelaide, production environments become ever more complex, particularly in deep water fields,
SA 5005, Australia the risk associated with injectivity impairment due to injection of seawater or re-injection
of produced water may increase to the point that production by conventional waterflood
may cease to be viable. Therefore, it is becoming increasingly important to predict injec-
C. J. A. Furtado tivity evolution under such circumstances. The work develops a semi-analytical model for
injectivity impairment during a suspension injection for the case of filtration and forma-
A. L.S. de Souza tion damage coefficients being linear functions of retained particle concentration. The
model exhibits limited retained particle accumulation, while the traditional model with a
Petrobras/CENPES, constant filtration coefficient predicts unlimited growth of retained particle concentration.
Av. Horatio Macedo 950, Cidade Universitaria, The developed model also predicts the well index stabilization after the decline
21941-915 - Rio de Janeiro, Brazil period. 关DOI: 10.1115/1.4002242兴
Keywords: injectivity, formation damage, analytical model, well index, deep bed
filtration
1 Introduction Analytical models for deep bed filtration have been presented
for the case of constant filtration and formation damage coeffi-
Injectivity decline is widely spread during waterflooding. One
cients for both linear flow geometry 共laboratory corefloods兲 and
of the main reasons for the phenomenon is the capture of solid and
axisymmetric flow 共flow around the vertical well兲 关6,9,10兴. The
liquid particles from injected aqueous suspension 共seawater, pro-
models exhibit unlimited growth of retained particle accumula-
duced water, or any poor quality water兲 resulting in reduction of
tion, which is physically unrealistic. Nevertheless, either coreflood
permeability and of injection well index 关1–4兴. The reliable pre-
or well data show the stabilized permeability with time. The ana-
diction of injectivity index decline is important for the planning lytical model for coreflood with blocking filtration function also
and design of well fracturing, acidizing, and other well stimula- exhibits the stabilized injectivity index 关6,11,12兴.
tion techniques. It is also important for the design of water man- In the current work, a semi-analytical model for axisymmetric
agement strategy for waterflood projects. flow around the vertical well is developed for a blocking filtration
Injection well behavior prediction under rock clogging due to function. The particle capture stops after reaching the maximum
injection of the colloid/suspension of particles is based on the 共critical兲 value by the retained concentration in each point of the
mathematical modeling of particle transport in porous media 关5,6兴. drainage volume. The injectivity index stabilizes when the re-
The main parameter determining kinetics of particle capture by tained concentration grows up to the critical value in a well neigh-
a porous matrix is the filtration coefficient, which is the ratio borhood.
between the particle retention rate and the module of the particle The structure of the paper is as follows. First, we describe the
flux 关6兴. The filtration coefficient is a probability for particles to mathematical model for suspension filtration and rock clogging
be captured during its transport over the unity distance. Depen- under Langmuir particle retention. Then, we discuss a semi-
dency of the filtration coefficient on the retained particle concen- analytical model for axisymmetric flow with detailed derivations.
tration is called the filtration function. Its form highly affects the Afterward, the results of impedance prediction with a sensitivity
injectivity decline. analysis are presented.
Different forms of filtration function have been presented in the
literature 关6,7兴. The constant filtration coefficient corresponds to
low retained concentrations, i.e., to the beginning of the well im- 2 Mathematical Model for Deep Bed Filtration
pairment process. The linear filtration function 共the so called During seawater injection, mainly solid particles penetrate into
blocking function兲 corresponds to Langmuir particle deposition, the reservoir; their retention in rock results in permeability decline
where the retention rate is proportional to the number of vacant and a consequent decrease in well injectivity index. Oily water
sites in the porous space and the matrix surface. The blocking injection during produced water re-injection 共PWRI兲 also results
filtration function is realized under intermediate retained concen- in injectivity impairment.
trations 关2,8兴. Different nonlinear shaped filtration functions have Deep bed filtration with similar modeling challenges occurs
been observed for highly clogged rocks 关7,8兴. during drilling fluid invasion into formation with consequent per-
meability damage 关13–15兴. It also occurs during produced water
disposal in aquifers 关16,17兴.
Contributed by the Petroleum Division of ASME for publication in the JOURNAL OF
ENERGY RESOURCES TECHNOLOGY. Manuscript received January 1, 2009; final manu-
It is assumed that all injected particles have the same filtration
script received June 7, 2009; published online October 7, 2010. Assoc. Editor: Desh- properties, allowing us to introduce the overall suspended and
eng Zhou. retained particle concentrations. Figure 1 shows the suspension
Journal of Energy Resources Technology Copyright © 2010 by ASME SEPTEMBER 2010, Vol. 132 / 033301-1
Downloaded From: http://energyresources.asmedigitalcollection.asme.org/ on 11/18/2017 Terms of Use: http://www.asme.org/about-asme/terms-of-use
The comparison between Eqs. 共2兲 and 共3兲 shows that the filtra-
tion function in Eq. 共3兲 is linear with respect to retention concen-
tration,
冉 冊
冦 冧
0 1 − , ⬍ m
共兲 = m
0, ⬎ m
If linear dependency in Eq. 共3兲 for 共兲 holds for the whole
interval of retention concentration variation, the maximum of re-
tention concentration m corresponds to the case where the overall
vacant grain surface is filled by particles; i.e., m is proportional
to the initial number of vacancies. If 共兲 is linear just for some
initial interval of and becomes nonlinear for larger values of
retained concentration, m is just a coefficient in the equation for
a straight line without any specific physics meaning.
So, the retention rate is characterized by two constants—by the
initial filtration coefficient 0 and by the maximum retention con-
centration m. Parameters 0 and m depend on the salinity and
pH of the injected water, on the mineral composition of grains, on
particle size, on its wettability, on temperature, etc.; i.e., two con-
stants are determined by the rock and the injected fluid.
If the retention concentration is negligibly smaller than the ini-
tial concentration of vacancies, the retained particles do not affect
the vacancy concentration and do not change the retention condi-
Fig. 1 Suspended and retained particle concentrations in po- tions, and the filtration function is constant. Formally, it corre-
rous space sponds to an infinite value of the maximum retention concentra-
tion m.
So called collective effects of particle interaction at high con-
centrations lead to the nonlinear filtration coefficient = 共兲. Its
concentration c of moving particles and the concentration of form depends on brine salinity, pH, electric Derjagin-Landau-
particles attached to grain surfaces and captured in thin throats by Verwey-Overbeek 共DLVO兲 forces, etc. 关20–22兴.
size exclusion. Particle retention results in permeability decrease; i.e., perme-
Following Refs. 关4,6,18,19兴, let us describe the mathematical ability is dependent:
model for flow of suspensions in porous media in the axisymmet-
ric geometry of vertical wells. q k0k共兲 p
The conservation of suspended and retained particles in porous =−
2rh r
media is
共4兲
c q c 1
+ 共1兲 k共兲 =
t 2rh r
=−
t 1 + 共1 + 2/兲
It is assumed that water is incompressible, and particle retention Different empirical formulas for permeability decrease with an
by rock does not change the total volume of the system “water increase in retained concentration have been proposed in the lit-
particles.” It results in the conservation of the flux q. erature 关14,22–26兴. Usually, a linear function of in the denomi-
Classical filtration theory assumes that the retention rate is pro- nator of Eq. 共4兲 with 2 = 0 is used in the expression for formation
portional to the particle advective flux cU, i.e., increase in either damage function k共兲, where  is called the formation damage
suspended concentration or velocity in number of times results in coefficient 关9,10兴.
the same number of times increase in the number of particles, A more general form of the denominator in Eq. 共4兲 with non-
which are transported to vacancies in rocks per unit of time. The zero 2 is used in Ref. 关24兴 to adjust coreflood injectivity impair-
proportionality coefficient depends on and is called the filtra- ment data. The case of Eq. 共4兲 corresponds to the linear function
tion function 共兲, of formation damage coefficient  versus retention concentration
, which corresponds to a quadratic polynomial for reciprocal to
q formation damage function k共兲. Further in the text, 2 is called
= 共兲c 共2兲 the second formation damage coefficient.
t 2rh The coefficients  and 2 are empirical constants characterizing
We assume that the capture rate is also proportional to the num- formation damage; they depend on the rock and the injected sus-
ber of vacancies 共Langmuir’s hypothesis兲. If A is a specific rock pension properties.
surface and b is an “individual” area on the grain surface engaged Systems 共1兲 and 共2兲 consist of two equations for two
by one retained particle, the vacancy concentration is proportional unknowns—c and . For the injection of constant concentration
to the free vacant surface, which equals A − b 共Fig. 1兲. suspension into a clean bed, systems 共1兲 and 共3兲 are subject to the
Finally, the retention rate is proportional to following initial and boundary conditions:
共A − b兲cU t = 0:c = = 0, r = rw:c = c0 共5兲
Introducing the proportionality coefficient yields the kinetic The boundary condition 共5兲 is set at the wellbore r = rw 共Fig. 2兲.
equation for retention rate, Introduce dimensionless coordinate and time
t
冉
= 0 1 −
c 冊
q
m 2rh
共3兲 X=
r2
R2c
, tD =
qt
hR2c
共6兲
033301-2 / Vol. 132, SEPTEMBER 2010 Transactions of the ASME
Downloaded From: http://energyresources.asmedigitalcollection.asme.org/ on 11/18/2017 Terms of Use: http://www.asme.org/about-asme/terms-of-use
3 Semi-Analytical Model for Axisymmetric Deep Bed
Filtration
Let us derive a semi-analytical solution for the axisymmetric
共radial兲 problem of deep bed filtration for any arbitrary filtration
function 共兲.
Introduce potential
冕
S
ds
⌽共S兲 = 共12兲
0
⌳共s兲
From Eq. 共9兲, it follows that
关2冑X⌽共S兲兴
C= 共13兲
tD
Substituting Eq. 共13兲 in Eq. 共8兲 yields
再 冑
tD tD
关2 X⌽共S兲兴 + 冎 再
冑
X tD
关2 X⌽共S兲兴 = −
S
tD
共14兲 冎
Changing the order of differentiation in the second term of Eq.
共14兲 results in
再 冎
Fig. 2 Schematic for injected suspension propagation be-
tween injection and production well: „a… contour radius is equal 冑 冑
to half-distance between injector and producer; „b… profile of 关2 X⌽共S兲兴 + 关2 X⌽共S兲兴 + S = 0 共15兲
tD tD X
suspension concentration is steady state behind the concen-
tration front; „c… gradual accumulation of retained particles be- The integration of Eq. 共15兲 in tD accounting for initial condi-
hind the concentration front tions 共11兲 yields
冑
tD
关2 X⌽共S兲兴 +
冑
X
关2 X⌽共S兲兴 + S =
冑
tD
关2 X⌽共S兲兴 再
The dimensionless time with the pore volumes injected 共p.v.i.兲
unit is identical to that in waterflooding, while the linear coordi-
nate X is equal to the square of the dimensionless radius 关26兴. The
+
冑
X
关2 X⌽共S兲兴 + S 冎 tD=0
共16兲
drainage radius is equal to the half-distance between injection and As it follows from initial conditions 共11兲, the right hand side of
production wells 共Fig. 2兲. Eq. 共16兲 is equal to zero; i.e., Eq. 共16兲 becomes
Substitution of Eq. 共6兲 along with dimensionless concentra-
tions, pressure, and filtration function 冑 冑
关2 X⌽共S兲兴 + 关2 X⌽共S兲兴 + S = 0 共17兲
tD X
c 4hk0 p
C= , S= , pD = , ⌳共S兲 = 共兲Rc 共7兲 So, the introduction of potential 共12兲 results in decreasing of the
c0 c0 q order of the partial differential equation of mass balance 共8兲 by 1.
Performing differentiation in Eq. 共17兲 accounting for Eq. 共12兲
into systems 共1兲, 共2兲, and 共4兲 yields results in
C C
+
tD X
=−
S
tD
共8兲
S S
+
tD X
= −冉⌽共S兲 ⌳共S兲
冑X − S 2冑X 冊 共18兲
The obtained first order hyperbolic Eq. 共18兲 can be solved by
method of characteristics.
S ⌳共S兲
= C 共9兲 Let us express first order partial differential Eq. 共18兲 in charac-
tD 2冑X teristic form,
tD
X pD =1 共19兲
1=− 共10兲 X
共1 + c0S + 2共c0兲2S2兲 X
Initial and boundary conditions 共5兲 for dimensionless variables
共Eqs. 共6兲 and 共7兲兲 take the form
dS
dX
= −冉⌽共S兲 ⌳共S兲
冑X − S 2冑X 冊 共20兲
From the boundary condition on the well 共Eq. 共11兲兲, it follows
tD = 0:C = S = 0 and X = XW = 共rW/Rc兲2:C = 1 共11兲 ⬘
that for any moment tD
Several analytical solutions of the problem 共Eqs. 共1兲, 共2兲, and
共5兲兲 have been reported in the literature 关6兴. A semi-analytical 2冑Xw⌽共S兲 = tD
⬘ 共21兲
solution for the clean bed injection problem 共Eq. 共5兲兲, for the case allowing expression of retained saturation on the wellbore
冉冑 冊
of filtration and formation damage coefficients linear with respect
to retention concentration, is presented in the next section. ⬘
tD
While the initial-boundary problem 共Eqs. 共1兲, 共2兲, and 共11兲兲 is ⬘ 兲 = ⌽−1
S共Xw,tD 共22兲
2 Xw
solved, pressure distribution along linear coordinate X during
flooding can be found from Eq. 共4兲 by a direct integration of the Here, ⌽−1 is an inverse function to ⌽共S兲 共see Eq. 共12兲兲.
pressure gradient in X from the well radius Xw to the contour As it follows from Eq. 共19兲, the characteristic line crossing any
radius Xc = 1. ⬘ 兲 共see also Fig. 3兲,
arbitrary point 共X , tD兲 also crosses point 共Xw , tD
Journal of Energy Resources Technology SEPTEMBER 2010, Vol. 132 / 033301-3
Downloaded From: http://energyresources.asmedigitalcollection.asme.org/ on 11/18/2017 Terms of Use: http://www.asme.org/about-asme/terms-of-use
The retained concentration behind the front is given by the
solution of the first order ordinary differential Eq. 共20兲. For the
case of the linear filtration function 共Eq. 共27兲兲, the solution is
given by formula 共29兲.
The solution S共X , tD兲 of the problem 共Eqs. 共29兲 and 共30兲兲 in the
behind-the-front region is obtained by the Runge–Kutta method.
The suspended concentration c共r , t兲 is obtained by Eq. 共9兲 using
the retained concentration s共r , t兲.
Figure 4 presents profiles of suspended and retained concentra-
tions, 共a兲 and 共b兲, respectively, at five different moments. The
values of injectivity damage coefficients and other parameters are
obtained in Ref. 关12兴 by the treatment of coreflood data 关27兴: 0
= 10 m−1,  = 100, 2 = −1000, m = 0.025, c0 = 10 ppm, Rc
= 500 m, rw = 0.1 m, and h = 30 m. The axes X for the profiles
extend from well X = Xw until the value that corresponds to r
Fig. 3 Concentration front and characteristic line on the plane = 0.5 m.
„X , tD… The suspended concentration gradually increases with time in
each reservoir point for the calculated case of linear filtration co-
efficient. This behavior is typical of the declining filtration
coefficient—the outlet concentration after the breakthrough re-
⬘ = tD − X + Xw
tD 共23兲 mains constant for a constant filtration coefficient. Gradual accu-
It results in the Cauchy condition for the ordinary differential Eq. mulation of retained concentration with time is shown in Fig. 4共b兲.
共20兲, The dimensionless pressure drop between injector and reservoir
冉 冊
共drawdown兲 is
tD − X + Xw
X = Xw:S = ⌽−1 共24兲
2冑Xw
冕
1
⌬P 1 pD
J= =− − dX 共32兲
Ordinary differential Eq. 共20兲 subject to Cauchy condition 共24兲 ⌬P0 ln共Xw兲 Xw
X
can be solved numerically.
Ahead of the concentration front X ⬎ X f = tD − Xw, suspended Let us express pressure gradient via deposited concentration
and retained concentrations are equal to zero. The retained con- from Eq. 共10兲 and substitute it into Eq. 共32兲,
冕 冕
centration is continuous along the front, S = 0, while the suspen- 1 1
sion concentration suffers discontinuity. Substituting Eq. 共9兲 into c0 S共X,tD兲  2共 c 0兲 2 S2共X,tD兲
Eq. 共8兲 and accounting for zero retained concentration on the sus- J共tD兲 = 1 − dX − dX
ln共Xw兲 Xw
X ln共Xw兲 Xw
X
pended concentration shock, we obtain
共33兲
C C ⌳共0兲
+ =− C 共25兲 The well impedance 共Eq. 共33兲兲 is obtained by numerical inte-
tD X 2冑X gration in X of expressions containing retained concentration dis-
Front X = Xw + tD is a characteristic line, which allows us to tribution S共X , tD兲, as calculated from Eqs. 共29兲 and 共30兲.
calculate suspended concentration behind the front from Eq. 共25兲,
C共X f 共tD兲,tD兲 = exp关− ⌳共0兲共冑X f − 冑Xw兲兴 = exp关− ⌳共0兲共冑Xw + tD
− 冑Xw兲兴
4 Calculations of Well Injectivity Index
共26兲
Let us show how to use formula 共33兲 and the values of four
Consider the particular case of linear filtration coefficient: injectivity damage parameters 0, m, , and 2, as obtained by
冉 冊
⌳共S兲 = 0Rc 1 −
S
Sm
共27兲
the treatment of coreflood data 关12兴, for well injectivity decline
prediction.
The model for vertical well injectivity decline consists of non-
The potential 共12兲 is linear deep bed filtration equations for axisymmetric flow geom-
⌽共S兲 = −
Sm
0R c
冉 冊
ln 1 −
S
Sm
共28兲
etry; see Eqs. 共1兲, 共3兲, and 共4兲. An exact semi-analytical solution
of the radial deep bed filtration problem 共Eqs. 共29兲 and 共30兲兲 al-
lows us to calculate well impedance versus time 共Eq. 共33兲兲.
Equation 共20兲 and the Cauchy condition become Figure 5 shows the sensitivity of the impedance curve with
冉 冉 冊 冊 冉 冊
respect to the second formation damage coefficient, while the fil-
dS Sm S 0R c S tration coefficient is constant; i.e., m tends to infinity. A 1 month
= ln 1 − −S 1− 共29兲
dX 冑
0R c X S m 冑
2 X S m injection period in Fig. 5共a兲 corresponds to 6 ⫻ 10−3 p.v.i. in Fig.
冋 冉 冊册
5共b兲. The default case corresponds to linear filtration with constant
0R c t D − X + X w filtration and formation damage coefficients, 0 = 10 m−1,  = 50,
X = Xw:S = Sm 1 − exp − 共30兲
Sm 2冑Xw and 2 = 0. Curves 2 and 3 correspond to values of the second
formation damage coefficient 2 = 200 and 2 = −200, respectively.
The structure of the suspension flow zone is shown in Fig. 3. The 2-values are in the range of those obtained from coreflood
Suspended and retained concentrations are equal to zero ahead of data 关27兴.
the front, which moves with carrier water velocity. Suspended If compared with the default case with 2 = 0, adding the qua-
concentration jumps from zero to the value of c−共r f , t兲 on the dratic term 22 with the positive 2 coefficient results in imped-
front. The suspended concentration behind the front is found from ance increase 共curve 2兲. Introduction of the quadratic term 22
the condition on the characteristic line with = 0, which coincides with the negative 2 coefficient results in impedance decrease
with the concentration front 关26兴: 共curve 3兲. The impedance curve is concave for the case of the
冋 冉冑
c−共r f 共t兲,t兲 = c0 exp − 共0兲 rw2 +
qt
h
− rw 冊册 共31兲
positive second formation damage coefficient and is convex for
negative 2. The significant difference between the impedance
033301-4 / Vol. 132, SEPTEMBER 2010 Transactions of the ASME
Downloaded From: http://energyresources.asmedigitalcollection.asme.org/ on 11/18/2017 Terms of Use: http://www.asme.org/about-asme/terms-of-use
Fig. 4 Dynamics of „a… suspended and „b… retained concentration profiles dur-
ing suspension injection in vertical well
curves with zero, positive, and negative 2 starts to appear after for retained concentration that is equal to the critical value m,
2 ⫻ 10−3 p.v.i. 共10 days兲. The curves almost coincide before the from Eq. 共33兲 follows formula for the maximum impedance,
injection of 10−3 p.v.
After 1 month of injection, the injectivity index decreases 2.4 J共t → ⬁兲 = 1 + m + 2m
2
共34兲
times for the constant formation damage coefficient 共2 = 0兲. It After the long-term injection, the injectivity index decreases
decreases 2.65 times for 2 = 200 and 2.15 times for 2 = −200. 6.0, 3.5, 2.3, and 1.1 times for curves 2–5, respectively.
Let us discuss the effect of the nonconstant filtration coefficient In offshore waterflood operations, the injectivity index stabili-
on impedance growth. Figure 6 presents impedance curves for zation at some reduced value happens quite often 关3,9,19兴. The
constant formation damage coefficients  = 50 and 2 = 0. The ini- usual explanation is well fracturing, where the fracture opens due
tial filtration coefficient 0 = 10 m−1. Curves 1–5 correspond to to high pressure near the injector because of reduced permeability;
the following values for maximum retained concentration: infinity, it propagates into the formation during further permeability de-
0.1, 0.05, 0.025, and 0.0015, respectively. So, the filtration func- cline and increase in hydraulic resistivity for leak-off. Another
tion decreases in order of the curve number increase. The larger explanation is erosion of external and internal filter cakes, where
the filtration function, the higher the retained particle concentra- the pressure gradient, increased due to permeability decline, drags
tion and the higher the impedance. Therefore, curves 1–5 follow particles from cakes in situ porous media and on the inner well
in the order of the impedance decrease. surface.
Curve 1 is linear due to the constant filtration coefficient. Im- Reaching the maximum retention concentration, where particle
pedance curves 2–5 stabilize with time; i.e., its time derivative capture by the rock does not happen anymore, is another explana-
tends to zero when time tends to infinity. It is explained by reach- tion of well injectivity index stabilization.
ing the maximum retention concentration m in each point around Let us compare the impedance growth curves for constant and
the well. The higher the distance to the point from the injector, the for linear filtration and formation damage functions. Straight line
later the maximum retention concentration will be reached. There- 1 in Fig. 7 corresponds to constant filtration and formation dam-
fore, curves 2–5 follow in order of decrease in the stabilization age coefficients: 0 = 10 m−1 and  = 50. For curves 2–6, values of
time. The moments of impedance stabilization are 200 days, 106 0 and  are the same as that for case 1.
days, 50 days, and 3 days, for curves 2–5, respectively. The second formation damage coefficient for curve 2 is equal to
Since the impedance function asymptotically reaches maximum 1000. For small retention concentrations at the beginning of in-
Journal of Energy Resources Technology SEPTEMBER 2010, Vol. 132 / 033301-5
Downloaded From: http://energyresources.asmedigitalcollection.asme.org/ on 11/18/2017 Terms of Use: http://www.asme.org/about-asme/terms-of-use
Fig. 5 Effect of two formation damage coefficients  and 2 on well imped-
ance curve: „a… impedance versus real time; „b… impedance versus p.v.i.
Fig. 6 Sensitivity of impedance curve to variation in filtration function: imped-
ance versus p.v.i.
033301-6 / Vol. 132, SEPTEMBER 2010 Transactions of the ASME
Downloaded From: http://energyresources.asmedigitalcollection.asme.org/ on 11/18/2017 Terms of Use: http://www.asme.org/about-asme/terms-of-use
Fig. 7 Monotonic and nonmonotonic impedance curves
jection, the values of filtration functions for cases 1 and 2 are ⬎ − / 22, the derivative is negative; accumulation of retained
almost equal. Due to the high value of the second formation dam- particles results in the reduction of hydraulic resistivity. This ef-
age coefficient for curve 2, it is located above the straight line 1 fect is physically unrealistic.
for small times. Curve 2 stabilizes with time, while the straight In case 4, m = 0.05, 2 = −1000, and  = 50; so, − / 22
line 1 grows unlimitedly. Therefore, at some moment, curve 2 = 0.025, which is less than m; i.e., the hydraulic resistivity in-
intersects line 1 and tends to a constant value at large times. creases for retention concentration varying from zero to 0.025 and
Curve 3 has a lower maximum retention concentration value if decreases afterward for retention concentration varying from
compared with curve 2. Therefore, curve 3 is located above line 1 0.025 to 0.05. Curve 4 decreases for ⬎ 0.025. This behavior is
and below curve 2 at small times. Curve 3 crosses line 1 and unrealistic. The paradox is caused by approximation of the forma-
stabilize faster than curve 2. tion damage function by the quadratic polynomial based on
The value of maximum retention concentration for curve 5 is J-values for small retention concentrations 共Fig. 8兲. If the depen-
lower than that for curve 3. Curve 5 is located above line 1 and dency = 共兲 has a negative second derivative, its approximation
below the curve 3 at small times. Curve 5 crosses line 1 and by the linear function 共3兲 causes the high value for the maximum
stabilize faster than curve 3. retained concentration 共Fig. 9兲, resulting in inequality m ⬎
Curves 2, 3, and 5 exhibit a monotonic growth. For positive − / 22. In this case, the model with linear filtration coefficient
-values and positive second formation damage coefficient, the 共3兲 is not valid.
derivative of reciprocal to formation damage function k共兲 共see For case 6, m = 0.025 and − / 22 = 0.025= m. During an in-
Eq. 共4兲兲 crease in retention concentration from zero to m, where tends
共22 +  + 1兲⬘ = 22 +  ⬎ 0 to m asymptotically, the hydraulic resistivity increases, which is
shown by the behavior of curve 6.
is always positive; i.e., the hydraulic resistance of retained par- Figure 10 presents injectivity index decline for the cases dis-
ticles increases during the deposition. cussed in Fig. 7. The declined form of injectivity index versus
Curves 4 and 6 correspond to the negative second formation time does allow distinguishing linear and nonlinear well behavior,
damage coefficient 2 = −1000. The derivative of the formation while the impedance plot clearly shows a linear well behavior for
damage function 22 +  is positive for low -values, i.e., for the case of constant injectivity damage coefficients and nonlinear
⬍ − / 22 共Fig. 8兲. For higher retention concentration values,
Fig. 8 Nonmonotonic behavior of reciprocal to formation dam-
age function due to linear interpolation of formation damage Fig. 9 Overestimated value of maximum retained concentra-
coefficient tion due to linear approximation of the filtration function
Journal of Energy Resources Technology SEPTEMBER 2010, Vol. 132 / 033301-7
Downloaded From: http://energyresources.asmedigitalcollection.asme.org/ on 11/18/2017 Terms of Use: http://www.asme.org/about-asme/terms-of-use
Fig. 10 Injectivity decline analysis using well index curves
curves for varying and . It shows the advantage to analyze The well behavior for constant injectivity damage parameters
injectivity impairment in coordinates “impedance versus time.” can be distinguished from that for linear function parameters by
The proposed three-point-pressure method 关12兴 can be imple- increasing impedance curves, not by declining well index curves.
mented into a simple, robust, and compact tool for applications in
on-site field conditions. Figure 11 shows the use of the tool at the Acknowledgment
sea platform. Direct measurements data of the rate and of pres-
sures in three core points are treated by the computer program The authors thank Petrobras for generous sponsorship of the
with optimization algorithm minimizing the deviation between the research project during many years and Dr. Farid Shecaira and
modeling and coreflood data. It allows us to determine the four Eng. Alexandre Guedes Siqueira 共Petrobras/CENPES兲 for fruitful
injectivity damage coefficients 0, m, , and 2 from coreflood support and encouragement. Many thanks are due to Prof. P. Cur-
data. Then, the impedance and well index are recalculated for the rie 共Delft University of Technology兲, Prof. Yannis Yortsos 共Uni-
axisymmetric flow of a vertical well 共Eq. 共33兲兲 and also for flow versity of Southern California兲, and Prof. A. Shapiro for fruitful
geometries of horizontal, fractured, and perforated wells using the discussions.
analytical solutions for 3D flow problems 关28兴.
Nomenclature
5 Conclusions
Injectivity decline due to rock clogging by the injected suspen- Latin Letters
sion with linear filtration and formation damage functions allows A ⫽ specific rock surface, 关L兴2
for semi-analytical modeling. b ⫽ area on grain surface filled by one retained
The impedance for injectivity damage parameters that are linear particle, 关L兴2
functions of the retained concentration monotonically increases c ⫽ suspension particle concentration
and asymptotically tends to a limit constant, while the impedance co ⫽ injected suspension concentration
for constant injectivity damage parameters linearly grows with h ⫽ formation thickness, 关L兴
time. II ⫽ injectivity index
The injectivity index stabilizes after the retained particle con- J ⫽ impedance
centration reaches its maximum value in some neighborhood of k ⫽ permeability, 关L兴2
the injector. L ⫽ core length, 关L兴
p ⫽ pressure, 关M兴关T兴−2关L兴−1
r ⫽ radius, 关L兴
Rc ⫽ drainage 共contour兲 radius, 关L兴
q ⫽ injection rate, 关L3 / T兴
t ⫽ time, 关T兴
U ⫽ Darcy velocity, 关L兴关T兴−1
x ⫽ coordinate in linear geometry, 关L兴
X ⫽ dimensionless coordinate in radial geometry
Greek Letters
 ⫽ formation damage coefficient
2 ⫽ formation damage coefficient
⫽ filtration coefficient 关L兴−1
Fig. 11 Using the three-point-pressure tool at sea platform 0 ⫽ value of filtration coefficient for = 0, 关L兴−1
033301-8 / Vol. 132, SEPTEMBER 2010 Transactions of the ASME
Downloaded From: http://energyresources.asmedigitalcollection.asme.org/ on 11/18/2017 Terms of Use: http://www.asme.org/about-asme/terms-of-use
⫽ viscosity of water, 关M兴关T兴−1关L兴−1 关13兴 Bailey, L., Boek, E. S., Jacques, S. D. M., Boassen, T., Selle, O. M., Argillier,
J.-F., and Longeron, D. G., 2000, “Particulate Invasion From Drilling Fluids,”
⫽ deposited particle concentration SPE J., 5共4兲, pp. 412–419.
⌽ ⫽ porosity 关14兴 Suryanarayana, P. V., Wu, Z., Ramalho, J., and Himes, R., 2007, “Dynamic
⌽ ⫽ potential Modelling of Invasion Damage and Impact on Production in Horizontal
Wells,” SPE Reservoir Eval. Eng., 10共4兲, pp. 348–358.
Superscripts/Subscripts 关15兴 Tang, Y., Yildiz, T., Ozkan, E., and Kelkar, M., 2005, “Effects of Formation
0 ⫽ initial Damage and High-Velocity Flow on the Productivity of Perforated Horizontal
Wells,” SPE Reservoir Eval. Eng., 8共4兲, pp. 315–324.
f ⫽ front 关16兴 Harding, T. G., Norris, B., and Smith, K. H., 2002, “Horizontal Water Disposal
m ⫽ maximum Well Performance in a High Porosity and Permeability Reservoir,” SPE Inter-
D ⫽ dimensionless national Thermal Operations and Heavy Oil Symposium and International
w ⫽ well Well Technology Conference, Calgary, Alberta, CA, Nov. 4–7, Paper No. SPE-
PSCIM/CHOA-79007.
关17兴 Harding, T. G., Varner, J., Flexhaug, L. A., and Bennion, D. B., 2003, “Design
References and Performance of a Water Disposal Well Stimulation Treatment in a High
Porosity and Permeability Sand,” Petroleum Society’s Canadian International
关1兴 Civan, F., 2006, Reservoir Formation Damage (Fundamentals, Modeling, As-
Petroleum Conference, Calgary, Alberta, CA, Jun. 10–12.
sessment, and Mitigation), 2nd ed., Gulf, Houston, TX, p. 742.
关2兴 Wojtanowicz, A. K., Krilov, Z., and Langlinais, J. P., 1987, “Study on the 关18兴 Rousseau, D., Hadi, L., and Nabzar, L., 2007, “PWRI-Induced Injectivity De-
Effect of Pore Blocking Mechanisms on Formation Damage,” Production Op- cline: New Insights on In-Depth Particle Deposition Mechanisms,” SPE Euro-
erations Symposium, Oklahoma City, OK, Mar. 8–10, Paper No. SPE 16233. pean Formation Damage Conference, Sheveningen, The Netherlands, May 30–
关3兴 Barkman, J. H., and Davidson, D. H., 1972, “Measuring Water Quality and Jun. 1, Paper No. SPE-07666.
Predicting Well Impairment,” JPT, 24共7兲, pp. 865–873. 关19兴 Wennberg, K. E., and Sharma, M. M., 1997, “Determination of the Filtration
关4兴 Sharma, M. M., and Yortsos, Y. C., 1987, “Transport of Particulate Suspen- Coefficient and the Transition Time for Water Injection Wells,” SPE European
sions in Porous Media: Model Formulation,” AIChE J., 33共10兲, pp. 1636– Formation Damage Conference, The Hague, The Netherlands, Jun. 2–3, Paper
1643. No. SPE-38181.
关5兴 Civan, F., 2007, “Formation Damage Mechanisms and Their Phenomenologi- 关20兴 Nabzar, L., Chauveteau, G., and Roque, C., 1996, “A New Model for Forma-
cal Modeling—An Overview,” European Formation Damage Conference, tion Damage by Particle Retention,” SPE Formation Damage Control Confer-
Sheveningen, The Netherlands, May 30–Jun. 1, Paper No. SPE-107857. ence, Lafayette, LA, Feb. 14–15, Paper No. SPE-311190.
关6兴 Herzig, J. P., Leclerc, D. M., and le Goff, P., 1970, “Flow of Suspensions 关21兴 Chauveteau, N. L., and Coste, J.-P., 1998, “Physics and Modelling of Perme-
Through Porous Media—Application to Deep Filtration,” Ind. Eng. Chem., ability Damage Induced by Particle Deposition,” SPE Formation Damage Con-
62共5兲, pp. 8–35. trol Conference, Lafayette, LA, Feb. 18–19, Paper No. SPE-39463.
关7兴 Alvarez, A. C., Bedrikovetsky, P., Hime, G., Marchesin, D., and Rodríguez, J. 关22兴 Wang, S., and Civan, F., 2005, “Modeling Formation Damage by Asphaltene
R., 2006, “A Fast Inverse Solver for the Filtration Function for Flow of Water Deposition During Primary Oil Recovery,” ASME J. Energy Resour. Technol.,
With Particles in Porous Media,” Inverse Probl., 22, pp. 69–88. 127共4兲, pp. 310–317.
关8兴 Kuhnen, F., Barmettler, K., Bhattacharjee, S., Elimelech, M., and Kretzschmar, 关23兴 Tiab, D., and Donaldson, E. C., 1996, Petrophysics—Theory and Practice of
R., 2000, “Transport of Iron Oxide Colloids in Packed Quartz Sand Media: Measuring Reservoir Rock and Fluid Transport Properties, Gulf, Houston,
Monolayer and Multilayer Deposition,” J. Colloid Interface Sci., 231, pp. TX, p. 706.
32–41. 关24兴 Al-Abduwani, F. A. H., Shirzadi, A., van den Broek, W. M. G. T., and Currie,
关9兴 Pang, S., and Sharma, M. M., 1997, “A Model for Predicting Injectivity De- P. K., 2005, “Formation Damage vs. Solid Particles Deposition Profile During
cline in Water-Injection Wells,” Paper No. SPEFE-28489, pp. 194–201. Laboratory-Simulated Produced-Water Reinjection,” SPEJ, 10共2兲, pp. 138–
关10兴 Bedrikovetsky, P., da Silva, M. J., da Silva, M. F., Siqueira, A. G., de Souza, 151.
A. L. S., and Furtado, C., 2005, “Well-History-Based Prediction of Injectivity 关25兴 Nabzar, L., Aguilera, M. E., and Rajoub, Y., 2005, “Experimental Study on
Decline During Seawater Flooding,” SPE Sixth European Formation Damage Asphaltene-Induced Formation Damage,” SPE International Symposium Oil-
Conference, Scheveningen, The Netherlands, May 25–27, Paper No. SPE- field Chemistry, Houston, TX, Feb. 2–4, Paper No. SPE-93062.
93886. 关26兴 Bedrikovetsky, P. G., 1993, Mathematical Theory of Oil and Gas Recovery,
关11兴 Soo, H., and Radke, C. J., 1986, “A Filtration Model for the Flow of Dilute, Kluwer Academic, Dordrecht.
Stable Emulsions in Porous Media—I Theory,” Chem. Eng. Sci., 41共2兲, pp. 关27兴 Todd, A. C., and Scott, G., 1984, “The Application of Depth of Formation
263–272. Damage Measurements in Predicting Water Injectivity Decline,” Formation
关12兴 Bedrikovetsky, P., Vaz, A. S. L., Jr., Furtado, C. A., and de Souza, A. L. S., Damage Control Symposium, Bakersfield, CA, Feb. 13–14, Paper No. SPE-
2008, “Formation Damage Evaluation From Non-Linear Skin Growth During 12498.
Coreflooding,” SPE International Symposium and Exhibition on Formation 关28兴 Bedrikovetsky, P., 2008, “Upscaling of Stochastic Micro Model for Suspen-
Damage Control, Lafayette, LA, Feb. 13–15, Paper No. SPE-112509. sion Transport in Porous Media,” Transp. Porous Media, 75共3兲, pp. 335–369.
Journal of Energy Resources Technology SEPTEMBER 2010, Vol. 132 / 033301-9
Downloaded From: http://energyresources.asmedigitalcollection.asme.org/ on 11/18/2017 Terms of Use: http://www.asme.org/about-asme/terms-of-use
Das könnte Ihnen auch gefallen
- The Nutritional Healing Series: - NH The Origins of DiseaseDokument31 SeitenThe Nutritional Healing Series: - NH The Origins of Diseaseunslaved100% (2)
- Fire-Resistant Hydraulic FL Uids - Water-Containing Re90223 - 2015-01 PDFDokument16 SeitenFire-Resistant Hydraulic FL Uids - Water-Containing Re90223 - 2015-01 PDFDennis Huanuco CcamaNoch keine Bewertungen
- Sustainable Urban PlanningDokument17 SeitenSustainable Urban PlanningBenito MosesNoch keine Bewertungen
- The Five Elements Book V50Dokument22 SeitenThe Five Elements Book V50Christopher CarrilloNoch keine Bewertungen
- Glaxo Vol IDokument164 SeitenGlaxo Vol IPrakash WarrierNoch keine Bewertungen
- Caustic Treatment of Jet FuelsDokument6 SeitenCaustic Treatment of Jet FuelsNishat M PatilNoch keine Bewertungen
- Bulacan Flooding SurveyDokument19 SeitenBulacan Flooding SurveyLJ GoNoch keine Bewertungen
- Amine Unit Start UpDokument11 SeitenAmine Unit Start UpthinkpadNoch keine Bewertungen
- Green Roof Design ConsiderationsDokument12 SeitenGreen Roof Design Considerationswaseq911Noch keine Bewertungen
- Effects of El Nino On The Agua Operations in Toril, Davao CityDokument7 SeitenEffects of El Nino On The Agua Operations in Toril, Davao CityJong AbearNoch keine Bewertungen
- Reverse Osmosis Treatment of Drinking WaterVon EverandReverse Osmosis Treatment of Drinking WaterBewertung: 3.5 von 5 Sternen3.5/5 (4)
- Design of A Methanol-To-Olefinprocess Using Aspen Hysys: Material and Energy BalancesDokument9 SeitenDesign of A Methanol-To-Olefinprocess Using Aspen Hysys: Material and Energy BalancesAbdulwahab GIWANoch keine Bewertungen
- Spe67234 PDFDokument6 SeitenSpe67234 PDFHai HoangNoch keine Bewertungen
- Monitoring Water FloodDokument9 SeitenMonitoring Water FloodRani Juliarini RahayuNoch keine Bewertungen
- Groundwater Quality Sampling at Contaminated Sites - The Long and The Short of It PDFDokument2 SeitenGroundwater Quality Sampling at Contaminated Sites - The Long and The Short of It PDFAnonymous Z7Lx7q0RzNoch keine Bewertungen
- Kal 4Dokument24 SeitenKal 4Nida AkNoch keine Bewertungen
- Mo2010 PDFDokument8 SeitenMo2010 PDFGaurav KumarNoch keine Bewertungen
- SPE 71582 Theory and Analysis of Injectivity Tests On Horizontal WellsDokument16 SeitenSPE 71582 Theory and Analysis of Injectivity Tests On Horizontal Wellsmohammad karimiNoch keine Bewertungen
- Effect of Coagulation Mechanism On Membrane Permeability in Coagulation-Assisted Microfiltration For Spent Filter Backwash Water Recycling PDFDokument7 SeitenEffect of Coagulation Mechanism On Membrane Permeability in Coagulation-Assisted Microfiltration For Spent Filter Backwash Water Recycling PDFAazar Ali ChannaNoch keine Bewertungen
- Influence of Pore Water Pressure To Seepage and Stability of Embankment Dam (Case Study of Sermo Dam Yogyakarta, Indonesia)Dokument5 SeitenInfluence of Pore Water Pressure To Seepage and Stability of Embankment Dam (Case Study of Sermo Dam Yogyakarta, Indonesia)Marsheal FisongaNoch keine Bewertungen
- SPE 108254 Investigation of Water-Coning Phenomenon in Iranian Carbonate Fractured ReservoirsDokument11 SeitenSPE 108254 Investigation of Water-Coning Phenomenon in Iranian Carbonate Fractured ReservoirsCole NathanielNoch keine Bewertungen
- Fractured Water-Injection Wells: A Pressure Falloff Test For Determining Fracture DimensionsDokument11 SeitenFractured Water-Injection Wells: A Pressure Falloff Test For Determining Fracture DimensionsMZNoch keine Bewertungen
- Estudio Calidad Agua Inyec Alasca y Tratamiento EstimulDokument10 SeitenEstudio Calidad Agua Inyec Alasca y Tratamiento EstimulHebert FerneynesNoch keine Bewertungen
- SPE93870 A Method For Pattern Recognition of WOR Plots in Waterflood ManagementDokument9 SeitenSPE93870 A Method For Pattern Recognition of WOR Plots in Waterflood ManagementJose Gregorio FariñasNoch keine Bewertungen
- A Study of Water Coning Control in Oil Wells by Flow BarriersDokument15 SeitenA Study of Water Coning Control in Oil Wells by Flow BarriersJorge F. CastañedaNoch keine Bewertungen
- SPE 106272 Small-Scale Fracture Conductivity Created by Modern Acid-Fracture FluidsDokument22 SeitenSPE 106272 Small-Scale Fracture Conductivity Created by Modern Acid-Fracture FluidsMemar AliNoch keine Bewertungen
- Reliable Simulation Model Permeability Arrays by Integration of Core, Test, and Log-Derived Permeability DataDokument11 SeitenReliable Simulation Model Permeability Arrays by Integration of Core, Test, and Log-Derived Permeability DataAiwarikiaarNoch keine Bewertungen
- Assessment of Secondary Clarification Design ConceptsDokument12 SeitenAssessment of Secondary Clarification Design Concepts305773253Noch keine Bewertungen
- Upscaling of Flow Units For Reservoir Flow Incorporating Small-Scale HeterogeneitiesDokument19 SeitenUpscaling of Flow Units For Reservoir Flow Incorporating Small-Scale HeterogeneitiessifatNoch keine Bewertungen
- Reduction of Sulphate Content in Aqueous Solutions by Reverse Osmosis Using Cellulose Acetate Membranes.Dokument6 SeitenReduction of Sulphate Content in Aqueous Solutions by Reverse Osmosis Using Cellulose Acetate Membranes.Andrea GeNoch keine Bewertungen
- Spe - Aime, Amoco Production Co.: Information Obtainable From Hterwell TracingDokument7 SeitenSpe - Aime, Amoco Production Co.: Information Obtainable From Hterwell TracingagihsalamNoch keine Bewertungen
- IPTC-13361-MS (December, 2009)Dokument14 SeitenIPTC-13361-MS (December, 2009)Lulut Fitra FalaNoch keine Bewertungen
- Journal of Dental Research: Water Absorption and Water Solubility of Soft Lining Materials For Acrylic DenturesDokument6 SeitenJournal of Dental Research: Water Absorption and Water Solubility of Soft Lining Materials For Acrylic DenturesANJALI TMU StudentNoch keine Bewertungen
- Spe 0719 0065 JPTDokument3 SeitenSpe 0719 0065 JPTDedipyaNoch keine Bewertungen
- Water ConingDokument13 SeitenWater ConingAminollah PayvandNoch keine Bewertungen
- 1 s2.0 S0011916424002868 MainDokument6 Seiten1 s2.0 S0011916424002868 MainPragadeesh SekarNoch keine Bewertungen
- Simulations of Full-Scale Reverse Osmosis MembraneDokument8 SeitenSimulations of Full-Scale Reverse Osmosis Membranezakaria aouamNoch keine Bewertungen
- 2006 13306Dokument39 Seiten2006 13306M-Amin RasaNoch keine Bewertungen
- Preliminary Experiment On Reservoir Sediment FlushingDokument8 SeitenPreliminary Experiment On Reservoir Sediment FlushingGamsan MNoch keine Bewertungen
- SPE-10690-MS-Mesuarion Well Profiles of PolymerDokument10 SeitenSPE-10690-MS-Mesuarion Well Profiles of PolymerMariaCamilaAcevedoCaballeroNoch keine Bewertungen
- Characterization of Activated Sludge Settling Properties With A Sludge Collapse-Acceleration StageDokument10 SeitenCharacterization of Activated Sludge Settling Properties With A Sludge Collapse-Acceleration StagepixulinoNoch keine Bewertungen
- JPSE Capture+diffusionDokument17 SeitenJPSE Capture+diffusionCatharina JenifferNoch keine Bewertungen
- X Ray CrystallographyDokument7 SeitenX Ray CrystallographyBlack JaguarNoch keine Bewertungen
- (Full Permission)Dokument11 Seiten(Full Permission)mohamadi42Noch keine Bewertungen
- Jordan 2008Dokument18 SeitenJordan 2008Nizam NazriNoch keine Bewertungen
- Wilson 2014Dokument4 SeitenWilson 2014Alex LutherNoch keine Bewertungen
- Phenomenology and Control of Buckling Dynamics in Multicomponent Colloidal DropletsDokument10 SeitenPhenomenology and Control of Buckling Dynamics in Multicomponent Colloidal DropletsDeepak sharmaNoch keine Bewertungen
- Marine and Petroleum Geology: Muhammad Fachri, Atle Rotevatn, Jan TverangerDokument21 SeitenMarine and Petroleum Geology: Muhammad Fachri, Atle Rotevatn, Jan TverangerAiwarikiaarNoch keine Bewertungen
- ARMA-2018-165 - Water Inyection With SAS Horizontal WellDokument8 SeitenARMA-2018-165 - Water Inyection With SAS Horizontal WellsddNoch keine Bewertungen
- Large-Eddy Simulations of Particle Sedimentation in A Longitudinal Sedimentation Basin of A Water Treatment Plant. Part 2: The Effects of Baf EsDokument7 SeitenLarge-Eddy Simulations of Particle Sedimentation in A Longitudinal Sedimentation Basin of A Water Treatment Plant. Part 2: The Effects of Baf Esallen alleniNoch keine Bewertungen
- Applied Thermal Engineering: Prediction of Caco Scaling in Water Injection WellboreDokument41 SeitenApplied Thermal Engineering: Prediction of Caco Scaling in Water Injection WellboreRezky FiqihNoch keine Bewertungen
- An Integrated Approach For Assessment of Water Holdup in A Multilayer Carbonate ReservoirDokument18 SeitenAn Integrated Approach For Assessment of Water Holdup in A Multilayer Carbonate ReservoirAhmad AdvinNoch keine Bewertungen
- Impact of Aeration On Mixed Liquor in Submerged‐ Membrane Bioreactors For Wastewater Treatment PDFDokument13 SeitenImpact of Aeration On Mixed Liquor in Submerged‐ Membrane Bioreactors For Wastewater Treatment PDFsulihah12Noch keine Bewertungen
- Desalination: C.J. Oliver, M.J. Davidson, R.I. NokesDokument8 SeitenDesalination: C.J. Oliver, M.J. Davidson, R.I. Nokesjean miguel oscorima celisNoch keine Bewertungen
- Jert 139 02 0229121Dokument9 SeitenJert 139 02 0229121Sina MadaniNoch keine Bewertungen
- Chemical Engineering Science: Brendan R. Gladman, Murray Rudman, Peter J. ScalesDokument10 SeitenChemical Engineering Science: Brendan R. Gladman, Murray Rudman, Peter J. ScalesDavid AndrésNoch keine Bewertungen
- Concentration Polarization in Cross-FlowDokument8 SeitenConcentration Polarization in Cross-FlowAlsultan AlsultanNoch keine Bewertungen
- Ambient To Insitu Poro PermDokument15 SeitenAmbient To Insitu Poro PermAjendra SinghNoch keine Bewertungen
- (Diff. P) 2021, Netherlands - Hydraulic Insights Into Rapid Sand Filter Bed Backwashing Using The Carman-Kozeny ModelDokument12 Seiten(Diff. P) 2021, Netherlands - Hydraulic Insights Into Rapid Sand Filter Bed Backwashing Using The Carman-Kozeny ModelMi doremiNoch keine Bewertungen
- Asaio 07Dokument10 SeitenAsaio 07kamsNoch keine Bewertungen
- Mathematical Modeling and Simulation of Concentration Polarization Layer in Reverse Osmosis ProcessDokument5 SeitenMathematical Modeling and Simulation of Concentration Polarization Layer in Reverse Osmosis ProcessSindhuja RaghunathanNoch keine Bewertungen
- SPE 71703 Capillary Pressure Data From NMR Logs and Its Implications On Field EconomicsDokument10 SeitenSPE 71703 Capillary Pressure Data From NMR Logs and Its Implications On Field Economicsdebashis22mNoch keine Bewertungen
- Gravelle 2014Dokument7 SeitenGravelle 2014lgaliziaNoch keine Bewertungen
- Abraham 2021 IOP Conf. Ser. Earth Environ. Sci. 655 012065-1Dokument8 SeitenAbraham 2021 IOP Conf. Ser. Earth Environ. Sci. 655 012065-1jonahotuankemeNoch keine Bewertungen
- APTES Dip and VaporDokument5 SeitenAPTES Dip and VaporSoft Matter LabNoch keine Bewertungen
- Characterizing Permeability With Formation TesterDokument22 SeitenCharacterizing Permeability With Formation TesterGede SiddiartaNoch keine Bewertungen
- Extended Abstract - ATippingDokument10 SeitenExtended Abstract - ATippingtareqsaed381Noch keine Bewertungen
- Buoyancy-Driven Motion of Drops and Bubbles inDokument23 SeitenBuoyancy-Driven Motion of Drops and Bubbles inddqylxgNoch keine Bewertungen
- Report Title:: Ilias@ncat - EduDokument10 SeitenReport Title:: Ilias@ncat - EduCholis ChobainNoch keine Bewertungen
- CP Modulus ReviewDokument21 SeitenCP Modulus ReviewTheoNoch keine Bewertungen
- Polymers 13 01765Dokument21 SeitenPolymers 13 01765curtis.colonestradaNoch keine Bewertungen
- Solving Nonlinear ODE and PDE Problems: Hans Petter LangtangenDokument57 SeitenSolving Nonlinear ODE and PDE Problems: Hans Petter LangtangenMusa MohammadNoch keine Bewertungen
- For General Purpose Research Simulator (GPRS)Dokument19 SeitenFor General Purpose Research Simulator (GPRS)Musa MohammadNoch keine Bewertungen
- Coding Exercis 3Dokument3 SeitenCoding Exercis 3Musa MohammadNoch keine Bewertungen
- Coding Exercise 1Dokument3 SeitenCoding Exercise 1Musa MohammadNoch keine Bewertungen
- Matplotlib CheatsheetsDokument2 SeitenMatplotlib CheatsheetsMusa MohammadNoch keine Bewertungen
- Installing and Using Tesseract 500 OCRFINALDokument4 SeitenInstalling and Using Tesseract 500 OCRFINALMusa MohammadNoch keine Bewertungen
- SWIGDocumentation PDFDokument505 SeitenSWIGDocumentation PDFMusa MohammadNoch keine Bewertungen
- A Backward Automatic Differentiation Framework For Reservoir SimulationDokument14 SeitenA Backward Automatic Differentiation Framework For Reservoir SimulationMusa MohammadNoch keine Bewertungen
- Optimization With Constraints: 2nd Edition, March 2004Dokument35 SeitenOptimization With Constraints: 2nd Edition, March 2004Musa MohammadNoch keine Bewertungen
- SPE-197369-MS Seismic Data Management For Big Data EraDokument9 SeitenSPE-197369-MS Seismic Data Management For Big Data EraMusa MohammadNoch keine Bewertungen
- Assessment of CO Storage Potential in Naturally Fractured Reservoirs With Dual-Porosity ModelsDokument42 SeitenAssessment of CO Storage Potential in Naturally Fractured Reservoirs With Dual-Porosity ModelsMusa MohammadNoch keine Bewertungen
- Open Source Exergy Calculation ToolDokument6 SeitenOpen Source Exergy Calculation ToolMusa MohammadNoch keine Bewertungen
- Modelling Geomechanical Impact of CO Injection Using Precomputed Response FunctionsDokument36 SeitenModelling Geomechanical Impact of CO Injection Using Precomputed Response FunctionsMusa MohammadNoch keine Bewertungen
- An Open-Source Toolchain For Simulation and Optimization of Aquifer-Wide CO StorageDokument10 SeitenAn Open-Source Toolchain For Simulation and Optimization of Aquifer-Wide CO StorageMusa MohammadNoch keine Bewertungen
- Comparison of Two-Phase Pipe Flow in Openfoam With A Mechanistic ModelDokument14 SeitenComparison of Two-Phase Pipe Flow in Openfoam With A Mechanistic ModelMusa MohammadNoch keine Bewertungen
- Public Cloud Storage For The Seismic Big Data Based On Amazon EC2 Cluster and HadoopDokument10 SeitenPublic Cloud Storage For The Seismic Big Data Based On Amazon EC2 Cluster and HadoopMusa MohammadNoch keine Bewertungen
- SPE-172381-MS Modeling Crude Oil Production Outlook: A Case Study of The Oil and Gas Industry in NigeriaDokument8 SeitenSPE-172381-MS Modeling Crude Oil Production Outlook: A Case Study of The Oil and Gas Industry in NigeriaMusa MohammadNoch keine Bewertungen
- Taurus PDFDokument639 SeitenTaurus PDFMusa MohammadNoch keine Bewertungen
- Introduction To Numpy Arrays: Gert-Ludwig IngoldDokument56 SeitenIntroduction To Numpy Arrays: Gert-Ludwig IngoldMusa MohammadNoch keine Bewertungen
- Are We There Yet?: A Deconstruction of Object-Oriented TimeDokument51 SeitenAre We There Yet?: A Deconstruction of Object-Oriented TimeMusa MohammadNoch keine Bewertungen
- AMOSS: A Bespoke Stochastic Simulation Environment Built On Open Source SoftwareDokument6 SeitenAMOSS: A Bespoke Stochastic Simulation Environment Built On Open Source SoftwareMusa MohammadNoch keine Bewertungen
- Suleiman's Trash TalkDokument2 SeitenSuleiman's Trash TalkMusa MohammadNoch keine Bewertungen
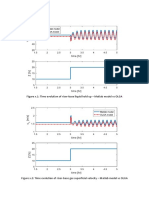
- Figure x.1: Time Evolution of Riser-Base Liquid Hold Up - Matlab Model Vs OLGADokument2 SeitenFigure x.1: Time Evolution of Riser-Base Liquid Hold Up - Matlab Model Vs OLGAMusa MohammadNoch keine Bewertungen
- Model Vs OLGADokument2 SeitenModel Vs OLGAMusa MohammadNoch keine Bewertungen
- 05-Information System For Conference ManagementDokument1 Seite05-Information System For Conference ManagementMusa MohammadNoch keine Bewertungen
- Lab 03Dokument14 SeitenLab 03Musa MohammadNoch keine Bewertungen
- 4 2 - FprENDokument85 Seiten4 2 - FprENraduvlasa100% (1)
- Honeywell Eyewash Infographic Draft04Dokument1 SeiteHoneywell Eyewash Infographic Draft04SatvikKumarNoch keine Bewertungen
- Heat of Fusion of WaterDokument6 SeitenHeat of Fusion of WaterAishaNoch keine Bewertungen
- Thermal Insulation Investigation 1 Higher Practice Exam QuestionsDokument4 SeitenThermal Insulation Investigation 1 Higher Practice Exam QuestionssayemaNoch keine Bewertungen
- B1996369-LI JING-Integrating Agro-Environmental Schemes Into Mainstream Agricultural PoliciesDokument89 SeitenB1996369-LI JING-Integrating Agro-Environmental Schemes Into Mainstream Agricultural PoliciesArthur ZhouNoch keine Bewertungen
- HS NC 123 PlusDokument6 SeitenHS NC 123 PlusFelipe cardenas villarrealNoch keine Bewertungen
- Vitec 4000 Antiscalant DatasheetDokument1 SeiteVitec 4000 Antiscalant DatasheetAnca MariaNoch keine Bewertungen
- Wedeco 400 SeriDokument4 SeitenWedeco 400 SeriAndrey GyrychNoch keine Bewertungen
- Technical System Data: Date/sign.: Rev. B: 24Aug06/KHE 1 01Apr11/KHEDokument5 SeitenTechnical System Data: Date/sign.: Rev. B: 24Aug06/KHE 1 01Apr11/KHEapalakNoch keine Bewertungen
- TTP - Irrigation Engineering - F16CE (B+D) - SMKDokument2 SeitenTTP - Irrigation Engineering - F16CE (B+D) - SMKazharNoch keine Bewertungen
- Fitting CatalogDokument28 SeitenFitting CatalognotreadyNoch keine Bewertungen
- Energy Efficiency in Historic BuildingsDokument17 SeitenEnergy Efficiency in Historic Buildingstexas_peteNoch keine Bewertungen
- REFERENSI 2 Ekstraksi Mekanik Esensial OilDokument9 SeitenREFERENSI 2 Ekstraksi Mekanik Esensial Oilaprilia fatma elyNoch keine Bewertungen
- MUIR - 2005 - A Practical Guide To Re-Treatment of Gold Processing ResiduesDokument14 SeitenMUIR - 2005 - A Practical Guide To Re-Treatment of Gold Processing ResiduesLeonardo RezendeNoch keine Bewertungen
- Sample Test Paper: For Stage - IDokument22 SeitenSample Test Paper: For Stage - IParth Anand100% (1)
- Ultratrex Presentation 2016Dokument26 SeitenUltratrex Presentation 2016cari halalNoch keine Bewertungen
- 3D TRASAR 3DT230 Cooling Water Corrosion and Deposit Inhibitor - PB - SP (English)Dokument4 Seiten3D TRASAR 3DT230 Cooling Water Corrosion and Deposit Inhibitor - PB - SP (English)ROBERTO BELTRANNoch keine Bewertungen
- DZR Automatic Air Vent ETA 4Dokument1 SeiteDZR Automatic Air Vent ETA 4Mohamed MansourNoch keine Bewertungen
- Erosion and SedimentationDokument11 SeitenErosion and SedimentationWindy RositaNoch keine Bewertungen