MATH 134, FALL 2007 HOMEWORK 4 SOLUTIONS

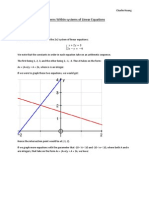
Ch. 4, ex. 1: (a) The trace is T = a and the determinant D = a2 /4 2 = T 2 /4 2. The graph of D as a function of T is a parabola, which can be obtained by shifting the critical parabola T 2 = 4D by two units down. (b) As a varies, bifurcations occur when the above parabola crosses the T = a-axis, i.e., when = 2 2. When a < 2 2, we have a real sink, when |a| < 2 2, a saddle, and for a a > 2 2, the phase portrait is a real source. Ch. 4, ex. 2: The trace is T = 2a and the determinant D = a2 b2 . The critical parabola T 2 = 4D in the ab-plane is the line b = 0, i.e., a-axis (since (2a)2 = 4(a2 b2 ) only if b = 0). Observe that we always have T 2 4D, so the eigenvalues are always real. Note that: {(T, D) : D > 0, T < 0} = {(a, b) : |a| > |b|, a < 0} This is summarized in the following gure: a = b b a=b {(T, D) : D < 0} = {(a, b) : |a| < |b|} (saddle) (real sink) (real source).

{(T, D) : D > 0, T > 0} = {(a, b) : |a| > |b|, a > 0}

saddle real sink real source a real sink saddle real source

Figure 1. Chapter 4, exercise 2. Ch.4, ex. 3: The corresponding system is X = AX with A= 0 1 . k b

The trace and determinant of A are T = b, D = k. So the (T, D)-plane equals (b, k)-plane with the orientiation of the b-axis reversed. Since b 0 and k > 0, the relevant region is the 2nd quadrant (T 0, D > 0) of Figure 4.1 on page 63.
1

Ch. 4, ex. 4: Denote the systems by X = AX and Y = BY . The map H is dened by H(X) = T X, where 1 0 . T = 0 1

(Note that T 2 = I and thus T 1 = T .) It is not hard to check that B = T 1 AT . Therefore, according to Section 3.4, T , i.e., H, sends solutions of Y = BY to solutions of X = AX. In other words, H is a linear conjugacy between these systems. Remark. So if matrices A and B are similar, then systems X = AX and Y = BY are conjugate. However, the opposite is not true, i.e., not every conjugacy is a similarity transformation between A and B.

Ch. 4, ex. 5(a): Denote the systems by X = AX and Y = BY . The eigenvalues of A are 1 and 2, while the eigenvalues of B are 2 and 1. A-eigenvectors corresponding to 1, 2 are 1 1 U1 = , U2 = , 0 3 respectively, while B-eigenvectors corrsponding to 2, 1 are V1 = 3 , 1 V2 = 0 , 1

respectively. Let P = [U1 |U2 ] and Q = [V1 |V2 ] be the associated matrices converting A and B to their canonical forms: 1 0 2 0 A0 = P 1 AP = and B0 = Q1 BQ = . 0 2 0 1 Then systems X = A0 X and Y = B0 Y are conjugate by a map H0 of the same type as that in the proof of Case 1 on page 67. Namely, let h0 (x) = x2 x2 if x 0 , if x < 0 g0 (y) = x1/2 |x|1/2 if x 0 . if x < 0

Then H0 (x, y) = (h0 (x), g0 (y)) is a topological conjugacy from X = A0 X to Y = B0 Y . We have the following commutative diagram: X = AX Y = BY Q P
H H

Therefore, the map

X = A0 X 0 Y = B0 Y.

H = Q H0 P 1 is a topological conjugacy from X = AX to Y = BY . Ch. 4, ex. 6: If A and B have the same eigenvalues i, then they have the same canonical form, 0 , 0

so they are clearly (linearly) conjugate. Suppose now that A has eigenvalues i and B has eigenvalues i, where can be dierent from . Both X = AX and Y = BY are

centers, so they should be conjugate. Without loss we can assume that A and B are in their canonical forms, 0 0 A= , B= . 0 0 Otherwise, we can rst convert them to canonical form, as in 5.(a). In polar coordinates (r, ) the ows A and B are given by t t This is because both ows simply rotate points around (0, 0), the former at angular speed , the latter at angular speed . Therefore, we are looking for a conjugacy that will change one speed to theh other. Dene H in polar coordinates by H(r, ) = r, . Since polar coordinates are not dened at the origin, set (in rectangular coordinates) H(0, 0) = (0, 0). Then: H(A (r, )) = H(r, t) t = r, ( t) = r, t = B r, t A (r, ) = (r, t), t B (r, ) = (r, t). t

= B (H(r, )). t It is clear that H is continuous away from the coordinate origin. Since |H(r, )| = r 0, as r 0, we get continuity also at the origin. If G(r, ) = r, and G takes the origin to itself, then it is not hard to check that G = H 1 . The continuity of G follows by the same argument as that for H. Therefore, H is a conjugacy from X = AX to Y = BY . This means that all systems with purely imaginary (nonzero) eigenvalues fall into one conjugacy class of centers. Remark. In complex coordinates the ows can be expressed as follows: A (z) = zeit , t The conjugacy H looks like this: H(z) = Note that |H(z)| = |z|. Ch. 4, ex. 7: Suppose M has exactly one zero eigenvalue. Denote the other, nonzero (and necessarily real) eigenvalue by . Since M has real distinct eigenvalues, its canonical form is 0 0 C = . 0 0
z / |z|/1

B (z) = zeit . t if z = 0 . if z = 0

Assume A and B both have exactly one zero eigenvalue, and denote their other eigenvalue by , , respectively. Then the associated canonical forms C , C give rise to conjugate systems X = C X, Y = C Y if and only if and have the same sign. Note that the ow of C is (x, y) = (x, yet ), so the conjugacy between X = C X and Y = C Y is t H(x, y) = (x, h(y)), where h is a map dened as in the Example on page 65 (i.e., h(x) = x/ , if x 0, and h(x) = |x|/ , if x < 0). So there are exactly two conjugacy classes corresponding to the sign of the nonzero eigenvalue. For < 0, all nonequilibrium solutions converge the the line of equilibria, and for > 0, they all diverge from it. Ch. 4, ex. 8: If both eigenvalues of a matrix A are zero, then there are two possibilities. Either A has two linearly independent eigenvalues or it doesnt. In the former case, A is the zero matrix, so every point is an equiibrium. In the latter case, the canonical form of A is 0 1 , 0 0 which gives rise to the ow t (x, y) = (x + ty, y). Since systems from these two dierent cases are clearly not conjugate, there are exactly two conjugacy classes. Ch. 4, ex. 9: If A is a nonhyperbolic matrix, then at least one of its eigenvalues has zero real part. There are three possible cases: Case 1: Both eigenvalues are zero. This case was discussed in exercise 8. There are exactly two 0 1 conjugacy classes corresponding to A = 0 and A = . 0 0 Case 2 Exactly one eigenvalue of A is zero. This was discussed in exercise 7. There are exactly two conjugacy classes corresponding to the sign of the nonzero eigenvalue. Case 3 The eigenvalues are purely imaginary, i, for = 0. This was discussed in exercise 7. There is exactly one conjugacy class of centers.