2

Electromagnetic Waves

2.1 Introduction
The term wave has no precise definition. It roughly corresponds to the idea of disturbances that travel. Although as physicist we tend to use the word mostly when referring to phenomena described by a wave equation, we also use it in other contexts. As an example of a more general use of the word, consider water waves, which only in the most crude approximation can be described by the linear wave equation that we will be discussing. What makes a water wave a wave is that disturbances such as the crests on the water surface propagate in a particular direction. Such traveling disturbances are associated with a net trans port of energy. In contrast, the medium supporting the waves, the water molecules, do not propagate. Instead the molecules collectively perform coordinated elliptical motions such that on the macroscopic scale a traveling water wave emerges. Other forms of waves are standing waves, where crests do not propagate but every point in space oscillates with a fixed amplitude. Of course one can intellectually decompose a standing wave into right and left traveling components but since on average no net transfer of energy takes place, standing waves and traveling waves are distinct. Electromagnetic waves, the very waves we want to study in this class have the distinguishing characteristic of occurring not only in matter but to also exist in vacuum. In the classical physics picture, vacuum is space devoid of any medium whose collective oscillations would give rise to the electromagnetic wave. This is certainly not an intuiti ve concept and it took physicists until the beginning of the 20th century to accept this fact.

2.2

Waves - 1D

Before starting to look at electromagnetic waves, let us review one-dimensional traveling waves. A very simple case of a right-traveling wave is depicted in Fig. 1. The

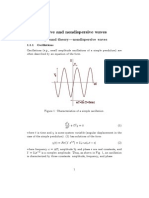
idea is that at any fixed moment in time the profile of the wave as a function of the space coordinate x is fixed but shifted to the right by an amou nt vt from initial profile at time t = 0. In other words = (x v t) for a right traveling the wave. Another way to say this is that a co-moving coordinate system, one in which the wave crest is always centered at x0 = 0, lets say, is given in terms of the original coordinates by x0 = x v t. The crest in the primed coordinate system is stationary at x0 = 0, consequently, in the original coordinate system it moves in time to larger x, x = v t.

Figure 1: Rig ht traveling wave of the form (xct). (This particular profile is given by 21 cosh[(x t)/2]2 . It is a solution to the linear wave equation, Eq. (4), as discussed in the text and, in addition, to the nonlinear Korte weg - de Vries equation, as discussed in the remark.)

Note that (x + v t) also describes a right traveling wave. A left traveling wave is defined by = (x + v t). (x v t) x + x(x + v t) 1 x v t 1 v 1 v (x v t) = t 0 t (x + v t) = (1) (2)

and since

1 2 1 2 + = x v t x2 v 2 t2

(3)

Figure 2: Right traveling periodic wave of the form sin(2[x ct 1/4]).

we can conclude that both right and left traveling waves are solutions to the one dimensional wave equation 2 1 2 = x2 v 2 t2 It is importa nt to note that Any function (x v t) is a solution. The initial conditions determine the and speed t (x, t = 0) = g(x), then the solution is uniquely determined Z x+v f (x vt) + f (x + vt) t (5) g(s)d (x, t) = 2 2c xv s 1 t + If there are, in addit ion, boundary conditions, then the possible solutions are constrained. For example, if the solution is fixed and zero at the boundary at x = 0 and x = L, i.e. (6) (0, t) = (L t) = , 0, then solutions are restricte d to those functions that can be written in terms of a Fourier series that only contains sin( nx/L) terms. (4)

 The wave equation is linear. If 1 (x, t) is a solution and 2 (x, t) is a solution, then so is their sum 1 (x, t) + 2 (x, t), where and are arbitrary consta nts. Why is linearity importa nt? It is importa nt because it means that one can decompose a solution of Eq. (4) into a sum of basis functions that are convenient. Linearity means that in such a decomposition the different basis functions dont interact. At any space-time point the solution is the algebraic sum of its components and the wave equation can be written as a set of independent (decoupled) wave equations, one for each basis function. We can Especially importa nt solutions to Eq. (4) are harmonic waves. = A sin(kx t + = A cos(kx t + 0 (7) ). 0 ) Using Eulers formula, we can write harmonic waves as the real and imaginary parts of (8) (x, t) = Aei(kxt+0 ) = Aei where 0 is the initial phase and (x, t) = kx t + 0 . An example of a right traveling harmonic wave is shown in Fig. 2. In the definition of the harmonic Frequency Wavelength Angular Frequency Propagation consta nt Wave speed/Phase speed = 2 2 |v| = = |k| |k| = (9) (10) (11) (12) (13)

For harmonic traveling waves the movement of the crests with wave speed |v| is identical to the rate at which the phase (x, t) propagates in space and | v| it is often called the phase speed. The absolute value sign is introduced here for consistency with later definitions where the sign of v is used to indicate propagation direction. However, for now let us consider v to be positive, v = |v|. Harmonic traveling waves are importa nt since they are periodic and because

 It is importa nt that the wave speed in Eq. (4) does not depend on the wave amplitude ||. It should be a consta nt in that respect, although it may depend on . Models where the propagation speed v depends on the wave amplitude v = v(||) result in nonlinear wave equations. These are much harder to solve than Eq. (4) but are often necessary to realistically model situations such as Remark: It is certainly true that all solutions of the wave equation, Eq. (4), have the general form (x v t) and any solution of that form satisfies Eq. (4). However, this does not imply that Eq. (4) is the only equation that gives rise to traveling solutions that have an unchanging profile and propagate with a consta nt speed v. That is, the obser vation of such a wave does not allow one to conclude that Eq. (4) is a good model for the underlying physical system. For example, solutions of the form (x v t) arise as particular solutions to nonlinear equations such as the Korteweg - de Vries equation, which describes shallow water waves, or the nonlinear Schrodinger equation, which is used to describe light propagation in optical fibers. Propagating solutions to nonlinear partial differential equations are referred to as solitons. An example is shown in Fig. 1. If viewed as a solution to Eq. (4), the displayed pulse is a traveling wave. Two such pulses that are counterpropagating would move through each other without interaction (lineari ty). If viewed as a solution to the nonlinear Korteweg - de Vries equation, the displayed pulse is a soliton. Two counterpropagating solitons would interact, a collision would take place. However, out of the collision the two solitons would reemerge

2.3

Waves - 3D

An obvious generalization of the 1D wave equation, Eq. (4), is the three dimensional wave equation 1 2 2 2 2 + + 2 2 2 (x, y, z, t) 2 2 y z v t = 0 x which can be made to look nicer by introducing the Laplacian operator 2 = 2 2 2 + + 2 x2 y 2 z (15) (14)

and using the three dimensional vector r to denote the space coordinates 2 2(r , t) 1 2 2 (r , t) = v t 0. (16)

2.3.1 Plane Waves

One of the most basic and importa nt solutions to the Eq. (16) are plane wav es. A right traveling plane wave in complex notation is (17) (r , t) = A ei(krt+0 ) = A ei The wave crests in this case are infinitely extended 2D planes in three dimensional space where the amplitude of is maximum, = A. In general, these planes are defined as the surfaces in space on which the phase is consta nt, just as in the case of 1D harmonic waves. The entire space is of course filled by a family of such planes. As time increases, these planes propagate through space with speed |v| = /|k|. The direction of propagation is given by the propagation vector (wave vector) k = kx x + ky y + (18) kz z The propagation vector k is normal to the surfaces of consta nt phase and is defined to point in the direction of propagation, parallel to v. It is often useful to write the vectors v and k in terms of their magnitude and direction, k = |k| v = |v| k k . where k is a unit vector. This provides consiste nt definitions, where the angular frequency k v = |k| |v| (k k ) = , is strictly positive, the phase factor for right traveling waves is given by k (r vt) = k r (21) t, and the phase factor for waves traveling in the opposite direction, left traveling waves, is (k) (r (v)t) = k (r + vt) = k r t, (22) (19)

(20)

leading to the most common way to express the complex plane wave solutions (r , t) = A eikr eit In the direction opposite to k (left): (r , t) = A eikr The sign in front of k indicates the propagat ion direction, left or right. In the direction of k (right): (23) (24)

Note that the plane wave is scalar and does not have any sense of orientat ion associated with it. That is, assigns a time dependent number (and not a vector) to every point in space. These numbers might describe, for example, air pressure variations induced by a plane sound wave. The complex notation is mathematically convenient because it is easier to deal with exponential functions than with sines and cosines. For convenience one also typically absorbs the phase consta nt 0 by redfining the amplitude A = A (25) i0 e , where A is now complex while A and 0 are real. Although complex wave functions are convenient, on should always keep in mind that the actual wave function is the real part of , (r , t) = A cos(k r t + 0 ). (26)