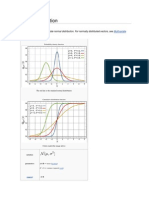
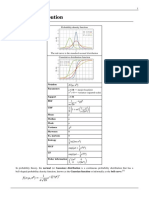
Log-normal distribution From Wikipedia, the free encyclopedia Log-normal Probability density function

Some functions identical location

logwith

normal density

parameter bu t differing scale parameters Cumulative distribution function

Cumulative distribution function of the log-normal distribution (with = 0 ) No ta tio n Pa 2 > ra shape m (real), et R er log-scale s Su x (0, +) pp or t 0

P DF C DF M ea n M ed ia n M od e Va ria nc e Sk e w ne ss Ex . ku rt os

is En tr op y M (defined GF only on the negative half-axis, see text) CF representat ion

is asymptotic ally divergent but sufficient for numerical purposes Fi sh er inf or m ati on

In probability theory, a log-normal distribution is a continuous probability distribution of a random variablewhose logarithm is normally distributed. If X is a random variable with a normal distribution, then Y = exp(X) has a log-normal distribution; likewise, if Y is lognormally distributed, then X = log(Y) is normally distributed. (This is true regardless of the base of the logarithmic function: if loga(Y) is normally distributed, then so is logb(Y), for any two positive numbers a, b 1.) Log-normal is also written log normal or lognormal. It is occasionally referred to as the Galton distribution orGalton's distribution, after Francis Galton. A variable might be modeled as log-normal if it can be thought of as the multiplicative product of many independentrandom variables each of which is positive. For example, in finance, the variable could represent the compound return from a sequence of many trades (each expressed as its return + 1); or a long-term discount factor can be derived from the product of short-term discount factors. In wireless communication, the attenuation caused by shadowing or slow fading from random objects is often assumed to be log-normally distributed: see log-distance path loss model. The log-normal distribution is the maximum entropy probability distribution for a random variate X for which the mean and variance of ln(X) is fixed. [1] [edit] and In a log-normal distribution X, the parameters denoted and, are the mean and standard deviation, respectively, of the variables natural logarithm (by definition, the variables logarithm is normally distributed), which means X = e + Z with Z a standard normal variable. On a non-logarithmized scale, and can be called the location parameter and the scale parameter, respectively. In contrast, the mean and standard deviation of the non-logarithmized sample values are denoted m and s.d.in this article. [edit]Characterization [edit]Probability density function

The probability density function of a log-normal distribution is:

This follows by applying the change-of-variables rule on the density function of a normal distribution. [edit]Cumulative distribution function

where erfc is the complementary error function, and is the standard normal cdf. [edit]Characteristic function and moment generating function The characteristic function, E[e itX], has a number of representations.[citation
needed]

The integral itself converges for Im(t) 0. The simplest representation

is obtained by Taylor expanding e itX and using formula for moments below, giving[citation needed]

This series representation is divergent for Re(2) > 0.[citation needed] However, it is sufficient for evaluating the characteristic function numerically at positive as long as the upper limit in the sum above is kept bounded,n N, where

and 2 < 0.1.[citation needed] To bring the numerical values of parameters , into the domain where strong inequality holds true one could use the fact that if X is log-normally distributed then Xm is also log-normally distributed with parameters m, m. Since , the inequality could be satisfied for sufficiently small m. The sum of series first converges to the value of (t) with arbitrary high accuracy if m is small enough, and left part of the strong inequality is satisfied. If considerably larger number of terms are taken into account the sum eventually diverges when the right part of the strong inequality is no longer valid.

Another useful representation was derived by Roy Lepnik[Full citation

needed]

(see references by this author and by Daniel Dufresne below)

by means of double Taylor expansion of e(ln x )2/(22). The moment-generating function for the log-normal distribution does not exist on the domain R, but only exists on the half-interval (, 0].
[citation needed]

[edit]Properties [edit]Location and scale For the log-normal distribution, the location and scale properties of the distribution are more readily treated using the geometric mean and geometric standard deviation than the arithmetic mean and standard deviation. [edit]Geometric moments The geometric mean of the log-normal distribution is e. Because the log of a log-normal variable is symmetric and quantiles are preserved under monotonic transformations, the geometric mean of a log-normal distribution is equal to its median.[2] The geometric mean (mg) can alternatively be derived from the arithmetic mean (ma) in a log-normal distribution by:

The geometric standard deviation is equal to e.[citation needed] [edit]Arithmetic moments If X is a lognormally distributed variable, its expected value (E which can be assumed to represent thearithmetic mean), variance (Var), and standard deviation (s.d.) are

Equivalently, parameters and can be obtained if the expected value and variance are known:

For any real or complex number s, the sth moment of lognormal X is given by

A log-normal distribution is not uniquely determined by its moments E[Xk] for k 1, that is, there exists some other distribution with the same moments for all k. In fact, there is a whole family of distributions with the same moments as the log-normal distribution. [edit]Mode and median

Comparison of mean, median and modeof two lognormal distributions with different skewness. The mode is the point of global maximum of the probability density function. In particular, it solves the equation (ln ) = 0:

The median is such a point where FX = 1/2:

[edit]Coefficient of variation The coefficient of variation is the ratio s.d. over m (on the natural scale) and is equal to:

[edit]Partial expectation The partial expectation of a random variable X with respect to a threshold k is defined as g(k) = E[X | X > k]P[X > k]. For a log-normal random variable the partial expectation is given by

This formula has applications in insurance and economics, it is used in solving the partial differential equation leading to the Black Scholes formula. [edit]Other A set of data that arises from the lognormal distribution has a symmetric Lorenz curve (see also Lorenz asymmetry coefficient).[3]