Beruflich Dokumente
Kultur Dokumente
LHV RDR
Hochgeladen von
Karl Rodney CerezoOriginalbeschreibung:
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
LHV RDR
Hochgeladen von
Karl Rodney CerezoCopyright:
Verfügbare Formate
K.R. Cerezo, R. Salvador Jr., A. Tajanlagit / Chem. Eng. Therm. Lab.
(2012)
ChE 124 Chemical Engineering Thermodynamics Laboratory Determination of the Latent Heat of Vaporization of Ethanol Using the Ramsay-Young Set-up
Karl Rodney Cerezo, Ruben Salvador Jr., Armin Tajanlangit*
Department of Chemical Engineering, University of the Philippines-Diliman, Quezon City, Philippines
ABSTRACT The experiment aimed to determine the latent heat of vaporization of 96% v/v Ethanol, through the use of the Ramsay-Young apparatus. The said setup allows experimenters to measure the boiling points of ethanol at different pressures. The experimental value, calculated to be 36235.7376 J/mol was then compared to three theoretical models: the Van der Waals, Redlich-Kwong and Keywords: Latent Heat of Vaporization, Ramsay-Young Apparatus, Equations of state, Saturation, Pressure the Soave-Redlich-Kwone Equations of state. Results were precise as the range of percent errors was 11.11% to 11.65%. The method has thus proven itself to be a viable way of determining the latent heat of vaporization, though great caution must be done in order to produce good results.
REPORT INFO Report History Revised Received Accepted
Table of Contents 1. Introduction .......................................................................................................................................................... 2 2. 3. 4. Materials and Equipment................................................................................................................................... 2 Experimental Design ........................................................................................................................................... 2 Results and Discussion ....................................................................................................................................... 4 Possible Sources of Error............................................................................................................................................ 5 5. Conclusion ............................................................................................................................................................. 5
References ........................................................................................................................................................................ 6
*Corresponding Author. Tel: +639177591779
Email Address: armintajanlangi@yahoo.com
K.R. Cerezo, R. Salvador Jr., A. Tajanlagit / Chem. Eng. Therm. Lab. (2012)
1. Introduction The latent heat of vaporization is defined as the amount of heat absorbed when a substance vaporizes from the liquid at constant temperature. No change in temperature occurs; however, a finite amount of heat is transferred into the substance.1 This experiment aims to determine the latent heat of vaporization of ethanol, through the use of the Ramsay-Young setup. The method involves boiling the substance at different pre-determined pressures, which are maintained as the substance is heated to the boiling point. The heats of vaporizations can then be calculated using the Clapeyron Equation. As shown by Smith, Van Ness and Abott [Introduction to Chemical Engineering Thermodynamics, 7th Ed., Mc Graw-Hill, New York. 2005], the latent heat of vaporization is directly proportional to the slope of the vapor pressure versus temperature curve. (1) Arranging the Clausius Equation to another form allows us to acquire the heat of vaporization under the assumptions that the vapor behaves ideally and the heat of vaporization is independent of temperature. (2) The slope of the plot of ln P vs 1/T will give a constant value of the latent heat of vaporization of ethanol. However with these assumptions, the heat of vaporization obtained will only be a rough estimate because: (1) The ethanol vapor does not behave as an ideal gas, and (2) the heat of vaporization of ethanol decreases with in increasing temperature and vice versa. With these conditions, the compressibility factor of the vapor should be taken into account. A more general form of the Clapeyron equation can be used, and Z values can
be calculated using the different equations of state.2 (3)
2. Materials and Equipment The experiment involves the following equipment and materials: i. Ramsay-Young Setup Vacuum Pump Manometer Flasks Rubber tubing Iron Clamps Thermocouple Hot plate/Bunsen burner 1000 ml, 500 ml, 50 ml beakers 50 ml EtOH Oil (for oil bath) and ice (for ice bath) Boiling chips
ii. iii. iv. v. vi. vii.
3. Experimental Design The Ramsay-Young apparatus (Figure 1) present in the laboratory is composed of a heated receiving flask (flask A) connected to a cooled collecting flask (flask B). The pressure of the entire system, sealed tight, is set with the use of a vacuum pump. From a container with a stopcock, the sample is allowed to drip into flask A where it is allowed to vaporize. The temperature where this vaporization occurs is monitored by a thermocouple whose sensor wires are inserted into flask A. The resulting vapors rise into flask B where the low temperature due to the surrounding ice bath returns the sample to its liquid form. This procedure is done over a series of
Smith, J., H.C., V. N., & Abbott, M. (2005). Introduction to Chemical Engineering Thermodynamics, 7th Edition. New York: Mc Graw-Hill.
Leonardo, M.C., Madlambayan, K., Peralta S. Determination of
the Latent Heat of Vaporization of Ethanol Using the RamsayYoung Set-up Experiment Proposal. 2011
K.R. Cerezo, R. Salvador Jr., A. Tajanlagit / Chem. Eng. Therm. Lab. (2012)
pressures, yielding a corresponding temperature for each pressure value (Garland & Shoemaker, 2003). The experiment started with the preheating of the hotplate under flask A. This was followed by the evacuation of the system to the highest pressure allowable. This facilitated easier pressure variation as in order to change the system pressure, the manometer valve simply had to be released. There was no need to start the pump again and again. This provided a set of descending pressure values during the experiment. After the evacuation, the sample was allowed to drip into flask A. Ideally, the sample should drip at a constant rate into flask A. if this ideal condition is met, the system will attain a constant temperature for a certain pressure even as the sample continues to drip. This is reflective of the fact that the latent heat of vaporization entails no temperature change. However, during the experiment, it was very difficult to keep the sample dripping at a constant rate. This inconsistent rise and fall in drop rate caused temperature to rise steadily. This was circumvented by adjustments in the actual procedure. Pressure remained set for a run while heating was continuously done without letting the sample drip. This caused the temperature to rise continuously. When the temperature had somehow stabilized (it changed slowly or only by fractions of degrees), a drop of sample was released into flask A. This suddenly brought system temperature down as the sample absorbed heat from the system. The reading to which temperature dropped was taken as the temperature reading at that pressure. Since vapor was visibly seen to have risen instantly from flask A, it was justifiably assumed that the sample absorbed its latent heat of vaporization from the system. This was done for a series of pressures,
starting from the highest possible pressure. For this run of the Latent Heat of Vaporization experiment, the assigned pressures (in inches Hg) are 2, 4, 6, and 8. The height difference of the surfaces of mercury in the two columns determines the pressure reading of the manometer. It should be noted that the manometer is not at its zero inches Hg mark. Detach the flasks from the set-up to clean and dry them properly. Procure 80 mL of EtOH and put it, together with some of the boiling chips, inside the first Florence flask. Put enough oil and the rest of the boiling chips in the 500-ml beaker and place it on top of the hotplate. Properly immerse the first Florence flask into the oil. Make sure that the oil would not overflow but is just enough so that there is contact between the oil and the smaller Florence flask. Fill a 1000-mL beaker with ice and immerse the second flask. After preparing the two Florence flasks, set-up the Ramsay-Young experiment. Make sure that the tubes are connected correctly, and the set-up is tightly sealed and no air escapes from the tube connections. Plug the vacuum pump into the transformer, and then plug the transformer and the hot plate in to the power outlet. The metal knob on the left side of the vacuum pump should be locked counter clockwise, and the knob located at the iron stand open (not locked clockwise) at the start of the experiment. Since all the necessary preparations have been made, the Ramsay-Young set-up is now ready to be operated. Turn on the transformer. Turn the vacuum pump on and slowly turn the valve of the vacuum pump until the reading of the manometer is 8.5 in Hg. Turn the pump off and close the knob located on the iron stand (by turning it clockwise). The manometer reading should be stable at this point. Slowly and simultaneously release the metal knob of the vacuum pump and the one at the iron stand until the height difference in the manometer reaches 8 in Hg. Close the knobs once the desired pressure is attained. Turn the thermocouple on and start heating the first flask by turning on and adjusting the heating temperature of the hotplate. Wait until the ethanol boils and the thermocouple reading becomes stable. Record the temperature
K.R. Cerezo, R. Salvador Jr., A. Tajanlagit / Chem. Eng. Therm. Lab. (2012)
and the operating pressure. Turn off the hotplate. Repeat the experiment for operating pressures of 6, 4, and 2 in Hg. When the experiment is complete, switch the transformer and hotplate off, remove the plugs, detach all the connecting tubes, dispose the Ethanol in its proper waste bottle, return the oil in its container, and wash all the glassware used in the experiment. 4. Results and Discussion During the experiment, the boiling temperature is recorded when the reading settles in order to satisfy equilibrium condition between the ambient pressure and the vapor pressure of liquid. The table below shows the boiling temperature for each pressure.
Determination of Hvap of Ethanol
11.8 11.75
ln(Psat)
11.7 11.65 11.6 11.55
0.00286 0.00287 0.00288 0.00289 0.0029 0.00291 0.00292 0.00293
1/T (K-1)
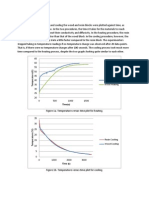
Figure 1. Plot derived from Clapeyron Equation Table 2. Equation of the Line Parameter Slope Intercept r2 Value -4358.4 2.587 0.9863
Table 1. Experimental Data Manometric (inHg) 7.65 5.9 3.9 1.9 Pressure Boiling Point (C) 68.95 71.25 73.45 75.2
To calculate for Hvap, the slope is multiplied to the negative of ideal gas constant, R=8.314 J/mol-K. The unit of the constant depends on the pressure and temperature units. Thus, the value of heat of vaporization is 36235.7376 J/mol. The value of r2 represents the discrepancy of assuming that the vapour is ideal and heat of vaporization is constant as temperature changes.
The setup uses a vacuum pump in order to operate at pressure less than 1 atm. In this condition, liquids will boil at lower temperature than the normal boiling point. In order to compute for the experimental heat of vaporization, the logarithm of Psat = Patm Pmanometric is related to inverse of boiling temperature which is based from the Clapeyron Equation (2). This yields a graph shown below:
In order to express the non-ideality of gas in terms of Z, Equations of State (EOS) are used which involves different parameters which is summarized below. Table 3. Parameter Assignments of Equations of State from (Smith et al., 2005) EOS (Tr) Zc vdW 1 0 0 1/8 27/64 3/8 RK Tr-1/2 1 0 .08664 .42748 1/3 SRK SRK 1 0 .08664 .42748 1/3 Where SRK = [( 1 + (0.480 + 1.54 - .176 2 )(1- Tr1/2 )]2 Using the models above, there are two possible values of z than can be calculated, one for saturated liquid and another for saturated vapor.
K.R. Cerezo, R. Salvador Jr., A. Tajanlagit / Chem. Eng. Therm. Lab. (2012)
The difference between the two z values yields and will be multiplied to RT2 . The last multiplier is and can be calculated using the Antoines equation of ethanol (where T is in C and Psat in kPa).
5 The enthalpy data above are shown with decreasing boiling temperature but the latent heat of vaporization should be decreasing steadily with temperature and is zero at the critical point. This discrepancy could be due to small number of data points for only four boiling temperatures are observed. Based from the table above, there is a significant difference when ethanol vapor is considered as non-ideal gas and its enthalpy changes with temperature. Comparing the three EOS, Van der Waals gives the highest enthalpy values while SRK gives the lowest, though their difference is not that significant. Possible Sources of Error Boiling chips provide nucleation sites in the liquid so that it boils smoothly without being superheated. If no boiling chips are used, it may cause rapid boiling and may cause the reagent to splatter and be expelled out of the flask. As the hotplate is heated, the operating pressure decreases. This may be due to the loose valves, an opening somewhere in the Ramsay-Young set-up or due to the behavior of the gas itself. Thus it should be ensured that the set-up is air tight and does not leak at any part (such as the tube connections, corks, etc.). This must be remedied by constantly adjusting the pressure since the experiment requires a condition of constant operating pressure. Failure to do so will cause a lower reading for the final pressure (P when Ethanol boils), thus constitutes to a value of Z nearer 1.0. The mercury inside the barometer should be at the zero inches mark. If not, the deviation from the zero mark should be taken into account in getting the difference of the two liquid levels to get the pressure reading. 5. Conclusion The Ramsay-Young method has so far proved to be a viable way of obtaining a substances Latent Heat of Vaporization. The calculations from the experiment data show good precision. Throughout the range of data points, the percent error ranges from 11.11% to 11.65% from all three theoretical models.
From the equation above, an expression of the differential is produced:
This gives the dependence of enthalpy of vaporization on temperature. Below is the summary of calculated Hvap using Van der Waals, RedlichKwong, and Soave-Redlich-Kwong equations.
Table 4.Comparison of EOS with Experimental Enthalpy (J/mol)
VDW Hvap 41014.95 40934.53 40858.1
%deviation 11.65237483 11.47879188 11.31321904
RK Hvap 41004.54 40923.7 40846.78 40785.41
%deviation 11.62995 11.45538 11.28864 11.15515
40797.26 11.18096001 SRK Hvap 40987.44 40905.84 40828.03 40765.71
%deviation 11.59307 11.41672 11.2479 11.11222
K.R. Cerezo, R. Salvador Jr., A. Tajanlagit / Chem. Eng. Therm. Lab. (2012)
References Levine, I. (2009). Physical Chemistry, 6th Ed. New York: McGraw-Hill, Inc. Maloney, J. (2008). Perry's Chemical Engineers' Handbook, 8th Ed. New York: Mc Graw-Hill, Inc. Poling, B., Prausnitz, J., & O'Connell, J. (2001). The Properties of Gases and Liquids, 5th Ed. New York: McGraw-Hill, Inc. Smith, J., H.C., V. N., & Abbott, M. (2005). Introduction to Chemical Engineering Thermodynamics, 7th Edition. New York: Mc Graw-Hill.
Das könnte Ihnen auch gefallen
- Phase Equilibrium in Mixtures: International Series of Monographs in Chemical EngineeringVon EverandPhase Equilibrium in Mixtures: International Series of Monographs in Chemical EngineeringNoch keine Bewertungen
- Punto de Ebullición - 1Dokument8 SeitenPunto de Ebullición - 1El Gil R GNoch keine Bewertungen
- Engineering Bulletin No 1: Boiler and Furnace TestingVon EverandEngineering Bulletin No 1: Boiler and Furnace TestingBewertung: 4.5 von 5 Sternen4.5/5 (2)
- Chemistry Lab-Enthalpy of Vaporization of Water Discussion and AnalysisDokument4 SeitenChemistry Lab-Enthalpy of Vaporization of Water Discussion and Analysislanichung100% (2)
- Respiration Calorimeters for Studying the Respiratory Exchange and Energy Transformations of ManVon EverandRespiration Calorimeters for Studying the Respiratory Exchange and Energy Transformations of ManNoch keine Bewertungen
- Enthalpy of Vaporization LabDokument5 SeitenEnthalpy of Vaporization LabDaniel LieNoch keine Bewertungen
- Clausius Clap LabDokument4 SeitenClausius Clap LabBunty MandaliaNoch keine Bewertungen
- Charles' LawDokument5 SeitenCharles' LawSuganya BaabuNoch keine Bewertungen
- Vapro Pressure and Heat Heat of VaporazationDokument5 SeitenVapro Pressure and Heat Heat of VaporazationStephen Rey CaldeaNoch keine Bewertungen
- Mercet BoilerDokument7 SeitenMercet BoilerDafiMaboNoch keine Bewertungen
- ReportDokument10 SeitenReportapi-272632563Noch keine Bewertungen
- ExperimentDokument5 SeitenExperimentJackson SonNoch keine Bewertungen
- Marcet Boiler Experiment (dT/dPDokument7 SeitenMarcet Boiler Experiment (dT/dPSiti Syuhadah100% (1)
- VLE - Furan / Carbon Tetrachloride: Experiment 9: Determination of Vapor-Liquid EquilibriumDokument5 SeitenVLE - Furan / Carbon Tetrachloride: Experiment 9: Determination of Vapor-Liquid EquilibriumAkshat RajNoch keine Bewertungen
- Marcet Boiler Lab ReportDokument27 SeitenMarcet Boiler Lab ReportamiraaikharahNoch keine Bewertungen
- Experiment P2: Bomb Calorimetry: Any Question On This Document ToDokument8 SeitenExperiment P2: Bomb Calorimetry: Any Question On This Document TomokilpoNoch keine Bewertungen
- High Pressure Calorimetry Application To Phase Change Under PressureDokument8 SeitenHigh Pressure Calorimetry Application To Phase Change Under PressureAlfonso DominguezNoch keine Bewertungen
- Relationship Between Pressure and Temperature of Saturated SteamDokument15 SeitenRelationship Between Pressure and Temperature of Saturated SteamSHADES 4 ALLNoch keine Bewertungen
- Calorimetry Is The Science of Measuring The Heat of Chemical Reactions or Physical ChangesDokument10 SeitenCalorimetry Is The Science of Measuring The Heat of Chemical Reactions or Physical ChangesBonaventure TuyishimeNoch keine Bewertungen
- Table of Contents ExperimentDokument6 SeitenTable of Contents ExperimentChooi San LaiNoch keine Bewertungen
- This Experiment Marcet Boiler Engineering EssayDokument11 SeitenThis Experiment Marcet Boiler Engineering EssayBerry101Noch keine Bewertungen
- Molecular Weight Determination by Vapour DensityDokument10 SeitenMolecular Weight Determination by Vapour DensityAnna LegaspiNoch keine Bewertungen
- Koç University Physical Chemistry Lab Experiments GuideDokument42 SeitenKoç University Physical Chemistry Lab Experiments GuideIreneVeladoNoch keine Bewertungen
- Measurement of The Gas Constant and Molar Volume of Oxygen GasDokument12 SeitenMeasurement of The Gas Constant and Molar Volume of Oxygen GasJennifer Im0% (1)
- IsoteniscopeDokument2 SeitenIsoteniscopeRolando R. MartinezNoch keine Bewertungen
- Heat Engines Lab ReportDokument3 SeitenHeat Engines Lab Reportapi-257546392Noch keine Bewertungen
- ENT 154 Thermodynamics Lab: Marcet Boiler ExperimentDokument9 SeitenENT 154 Thermodynamics Lab: Marcet Boiler Experimentcog0812Noch keine Bewertungen
- Enthalpy of Combustion via Calorimetry ExperimentDokument8 SeitenEnthalpy of Combustion via Calorimetry ExperimentJohnPholTalabanNoch keine Bewertungen
- CHE486 - Marcet BoilerDokument6 SeitenCHE486 - Marcet BoilerHaikal SuhaimiNoch keine Bewertungen
- TH3 Saturation Pressure Experiment GuideDokument12 SeitenTH3 Saturation Pressure Experiment GuideChelseaNoch keine Bewertungen
- Calorimeter Specific Heat TestDokument2 SeitenCalorimeter Specific Heat TestDiego Fernado AvendañoNoch keine Bewertungen
- Marcet BoilerDokument18 SeitenMarcet BoilerCendolz IssZulNoch keine Bewertungen
- 900 1000 Sea Level Atmospheric Pressure Vapor Pressure, MM/HGDokument5 Seiten900 1000 Sea Level Atmospheric Pressure Vapor Pressure, MM/HGLexey Utlang100% (1)
- ReportDokument7 SeitenReportShōyōHinataNoch keine Bewertungen
- Exp 8 Ideal Gas LawDokument7 SeitenExp 8 Ideal Gas LawEzat Rahman0% (1)
- Lab 5 Enthalpy of VaporizationDokument4 SeitenLab 5 Enthalpy of VaporizationFrolian MichaelNoch keine Bewertungen
- Bomb CalorimeterDokument4 SeitenBomb Calorimeteruserh1911100% (1)
- Marcet BoilerDokument10 SeitenMarcet BoilerMD Atiqur Rahman Faisal100% (14)
- Marcet BoilerDokument9 SeitenMarcet BoilerKayfe sayfadeenNoch keine Bewertungen
- Marcet Boiler Lab ReportDokument12 SeitenMarcet Boiler Lab ReportShameerSamsuriNoch keine Bewertungen
- CONCLUSION & Reco Exp Heat PumpDokument2 SeitenCONCLUSION & Reco Exp Heat PumpAfiqaiman ZainalNoch keine Bewertungen
- Practicas Lab de FisicoquimicaDokument113 SeitenPracticas Lab de FisicoquimicaAiled González SánchezNoch keine Bewertungen
- E4 - Marcet Boiler - NewDokument7 SeitenE4 - Marcet Boiler - NewSalahuddin NorazmiNoch keine Bewertungen
- Merce T Boiler ExperimentDokument14 SeitenMerce T Boiler ExperimentjevaughnNoch keine Bewertungen
- Vapour Pressure LabDokument3 SeitenVapour Pressure Labapi-235688447Noch keine Bewertungen
- 2423L3Dokument8 Seiten2423L3Ruben SyNoch keine Bewertungen
- IdkbraaaaaaahDokument4 SeitenIdkbraaaaaaahE22ZNoch keine Bewertungen
- AP Chemistry - Vaporization Pressure LabDokument5 SeitenAP Chemistry - Vaporization Pressure LabJonathan ChenNoch keine Bewertungen
- Experiment 8 Gas Laws: Figure 1: Amontons' Law ApparatusDokument9 SeitenExperiment 8 Gas Laws: Figure 1: Amontons' Law ApparatusRichard Balbin Jr.Noch keine Bewertungen
- Marcet BoilerDokument10 SeitenMarcet BoilerDhia EmpayarNoch keine Bewertungen
- Bachelor of Engineering (Hons) Chemical Che 465 Chemical Engineering Laboratory IDokument14 SeitenBachelor of Engineering (Hons) Chemical Che 465 Chemical Engineering Laboratory IRobert HarrisNoch keine Bewertungen
- Raoult LawDokument17 SeitenRaoult LawAle AlvarezNoch keine Bewertungen
- Enthalpies of ReactionDokument10 SeitenEnthalpies of ReactionJanin CustodioNoch keine Bewertungen
- Thermo CalibrationDokument10 SeitenThermo CalibrationAngelo De AsisNoch keine Bewertungen
- Trifon Ov Ivanov 2003Dokument5 SeitenTrifon Ov Ivanov 2003ArnoldoNoch keine Bewertungen
- Marcet BoilerDokument7 SeitenMarcet BoilerSt Oong100% (1)
- Boyle's Law Lab Report 4Dokument10 SeitenBoyle's Law Lab Report 4Abdul MannanNoch keine Bewertungen
- Thermo ManualDokument24 SeitenThermo ManualRajakhalidNoch keine Bewertungen
- Ammonia: Latent Heat of OFDokument34 SeitenAmmonia: Latent Heat of OFCastoriadisNoch keine Bewertungen
- EMLa Ancsin R11 Cryostat TChA 1996Dokument6 SeitenEMLa Ancsin R11 Cryostat TChA 1996emendez56Noch keine Bewertungen
- Calculating Vessel Surface AreaDokument1 SeiteCalculating Vessel Surface Areanavneet21100% (1)
- Antoine ConstantsDokument1 SeiteAntoine Constantsradwaelhadad75% (8)
- Reciprocating Compressor4Dokument19 SeitenReciprocating Compressor4Vijay AcharyaNoch keine Bewertungen
- Antoine ConstantsDokument1 SeiteAntoine Constantsradwaelhadad75% (8)
- Some Problems in Reaction KineticsDokument5 SeitenSome Problems in Reaction KineticsKarl Rodney CerezoNoch keine Bewertungen
- Thermal Diff RDRDokument7 SeitenThermal Diff RDRKarl Rodney CerezoNoch keine Bewertungen
- Case Presentation - Bipolar Affective Disorder 2Dokument73 SeitenCase Presentation - Bipolar Affective Disorder 2Hemant's galaxy All is hereNoch keine Bewertungen
- Extraform RsDokument47 SeitenExtraform RsCarlos David Duran AvilaNoch keine Bewertungen
- Lending Tree PDFDokument14 SeitenLending Tree PDFAlex OanonoNoch keine Bewertungen
- Plants Life Cycles and PartsDokument5 SeitenPlants Life Cycles and PartsseemaNoch keine Bewertungen
- 1 20《经济学家》读译参考Dokument62 Seiten1 20《经济学家》读译参考xinying94Noch keine Bewertungen
- Programming Language II CSE-215: Dr. Mohammad Abu Yousuf Yousuf@juniv - EduDokument34 SeitenProgramming Language II CSE-215: Dr. Mohammad Abu Yousuf Yousuf@juniv - EduNaruto DragneelNoch keine Bewertungen
- Cypress Enable Basic Rer Erence ManualDokument2 SeitenCypress Enable Basic Rer Erence ManualCarlos RodasNoch keine Bewertungen
- Effects of War On EconomyDokument7 SeitenEffects of War On Economyapi-3721555100% (1)
- SRS documentation of Virtual Classroom System , SRS documentation of Personal Identity Management ,SRS documentation of EMentoring for women system , SRS Documentation of Employee Performance Management SRS Documentation of Online TicketingDokument79 SeitenSRS documentation of Virtual Classroom System , SRS documentation of Personal Identity Management ,SRS documentation of EMentoring for women system , SRS Documentation of Employee Performance Management SRS Documentation of Online Ticketingsaravanakumar1896% (26)
- Impression Techniques in Complete Denture Patients: A ReviewDokument6 SeitenImpression Techniques in Complete Denture Patients: A ReviewRoja AllampallyNoch keine Bewertungen
- Mercury QCDokument23 SeitenMercury QCMarcus MeyerNoch keine Bewertungen
- SSNDokument1.377 SeitenSSNBrymo Suarez100% (9)
- 6a. ICMR STSDokument15 Seiten6a. ICMR STSVishnu Praba ANoch keine Bewertungen
- Löwenstein Medical: Intensive Care VentilationDokument16 SeitenLöwenstein Medical: Intensive Care VentilationAlina Pedraza100% (1)
- Women Safety AppDokument18 SeitenWomen Safety AppVinod BawaneNoch keine Bewertungen
- 2 Case StudyDokument8 Seiten2 Case Studysehrish khawerNoch keine Bewertungen
- AI Search Iterative DeepeningDokument4 SeitenAI Search Iterative DeepeningNirjal DhamalaNoch keine Bewertungen
- Solidwork Flow Simulation TutorialDokument298 SeitenSolidwork Flow Simulation TutorialMilad Ah100% (8)
- Complex Numbers GuideDokument17 SeitenComplex Numbers GuideGus EdiNoch keine Bewertungen
- UK Commutator Maintenance CatalogueDokument9 SeitenUK Commutator Maintenance CatalogueCarlosNoch keine Bewertungen
- An Improved Ant Colony Algorithm and Its ApplicatiDokument10 SeitenAn Improved Ant Colony Algorithm and Its ApplicatiI n T e R e Y eNoch keine Bewertungen
- Network Theory - BASICS - : By: Mr. Vinod SalunkheDokument17 SeitenNetwork Theory - BASICS - : By: Mr. Vinod Salunkhevinod SALUNKHENoch keine Bewertungen
- Indra: Detail Pre-Commissioning Procedure For Service Test of Service Water For Unit 040/041/042/043Dokument28 SeitenIndra: Detail Pre-Commissioning Procedure For Service Test of Service Water For Unit 040/041/042/043AnhTuấnPhanNoch keine Bewertungen
- Maturity Mode Agile BookDokument110 SeitenMaturity Mode Agile BookSai VenkatNoch keine Bewertungen
- O-L English - Model Paper - Colombo ZoneDokument6 SeitenO-L English - Model Paper - Colombo ZoneJAYANI JAYAWARDHANA100% (4)
- Microwave: Microwaves Are A Form ofDokument9 SeitenMicrowave: Microwaves Are A Form ofDhanmeet KaurNoch keine Bewertungen
- PH Miracle Complete Whole Body Alkalizing Program-1201724Dokument20 SeitenPH Miracle Complete Whole Body Alkalizing Program-1201724joao carlos100% (1)
- Irc SP 65-2005 PDFDokument32 SeitenIrc SP 65-2005 PDFAjay Kumar JainNoch keine Bewertungen
- Stress Out?: A Study of Trends in Workplace Stress Across The GlobeDokument14 SeitenStress Out?: A Study of Trends in Workplace Stress Across The GlobeVishesh Vij100% (1)
- SWOT AnalysisDokument6 SeitenSWOT Analysishananshahid96Noch keine Bewertungen
- Lees' Process Safety Essentials: Hazard Identification, Assessment and ControlVon EverandLees' Process Safety Essentials: Hazard Identification, Assessment and ControlBewertung: 4 von 5 Sternen4/5 (4)
- Piping and Pipeline Calculations Manual: Construction, Design Fabrication and ExaminationVon EverandPiping and Pipeline Calculations Manual: Construction, Design Fabrication and ExaminationBewertung: 4 von 5 Sternen4/5 (18)
- Process Plant Equipment: Operation, Control, and ReliabilityVon EverandProcess Plant Equipment: Operation, Control, and ReliabilityBewertung: 5 von 5 Sternen5/5 (1)
- An Introduction to the Periodic Table of Elements : Chemistry Textbook Grade 8 | Children's Chemistry BooksVon EverandAn Introduction to the Periodic Table of Elements : Chemistry Textbook Grade 8 | Children's Chemistry BooksBewertung: 5 von 5 Sternen5/5 (1)
- Functional Safety from Scratch: A Practical Guide to Process Industry ApplicationsVon EverandFunctional Safety from Scratch: A Practical Guide to Process Industry ApplicationsNoch keine Bewertungen
- Guidelines for the Management of Change for Process SafetyVon EverandGuidelines for the Management of Change for Process SafetyNoch keine Bewertungen
- Chemical Process Safety: Learning from Case HistoriesVon EverandChemical Process Safety: Learning from Case HistoriesBewertung: 4 von 5 Sternen4/5 (14)
- Well Control for Completions and InterventionsVon EverandWell Control for Completions and InterventionsBewertung: 4 von 5 Sternen4/5 (10)
- Nuclear Energy in the 21st Century: World Nuclear University PressVon EverandNuclear Energy in the 21st Century: World Nuclear University PressBewertung: 4.5 von 5 Sternen4.5/5 (3)
- Process Engineering for a Small Planet: How to Reuse, Re-Purpose, and Retrofit Existing Process EquipmentVon EverandProcess Engineering for a Small Planet: How to Reuse, Re-Purpose, and Retrofit Existing Process EquipmentNoch keine Bewertungen
- Guidelines for Siting and Layout of FacilitiesVon EverandGuidelines for Siting and Layout of FacilitiesNoch keine Bewertungen
- Operational Excellence: Journey to Creating Sustainable ValueVon EverandOperational Excellence: Journey to Creating Sustainable ValueNoch keine Bewertungen
- Guidelines for Engineering Design for Process SafetyVon EverandGuidelines for Engineering Design for Process SafetyNoch keine Bewertungen
- Guidelines for Developing Quantitative Safety Risk CriteriaVon EverandGuidelines for Developing Quantitative Safety Risk CriteriaNoch keine Bewertungen
- Process Steam Systems: A Practical Guide for Operators, Maintainers, and DesignersVon EverandProcess Steam Systems: A Practical Guide for Operators, Maintainers, and DesignersNoch keine Bewertungen
- Bow Ties in Risk Management: A Concept Book for Process SafetyVon EverandBow Ties in Risk Management: A Concept Book for Process SafetyNoch keine Bewertungen
- Guidelines for Enabling Conditions and Conditional Modifiers in Layer of Protection AnalysisVon EverandGuidelines for Enabling Conditions and Conditional Modifiers in Layer of Protection AnalysisNoch keine Bewertungen
- Perfume Engineering: Design, Performance and ClassificationVon EverandPerfume Engineering: Design, Performance and ClassificationBewertung: 4 von 5 Sternen4/5 (5)
- Fragrance Chemistry: The Science of the Sense of SmellVon EverandFragrance Chemistry: The Science of the Sense of SmellBewertung: 3 von 5 Sternen3/5 (2)
- Practical Process Control for Engineers and TechniciansVon EverandPractical Process Control for Engineers and TechniciansBewertung: 5 von 5 Sternen5/5 (3)
- Temperature-Responsive Polymers: Chemistry, Properties, and ApplicationsVon EverandTemperature-Responsive Polymers: Chemistry, Properties, and ApplicationsNoch keine Bewertungen