Beruflich Dokumente
Kultur Dokumente
QF I Lecture4
Hochgeladen von
Nikolay KolarovOriginalbeschreibung:
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
QF I Lecture4
Hochgeladen von
Nikolay KolarovCopyright:
Verfügbare Formate
Quantitative Finance I
Modeling Volatility (Lecture 4)
Winter Semester 2011/2012 by Lukas Vacha and Jozef Barunk
* If viewed in .pdf format - for full functionality use Mathematica 7 notebook (.nb) version of this .pdf
Characteristics of Volatility
Volatility is one of the most important concepts in finance, as it measures the risk of financial assets. Altough volatility is not directly observable, and can be just estimated, it has some important characteristics: (i) volatility clusters - there are periods of high/low volatility (ii) volatility evolves over time continuously (jumps in volatility are rare) (iii) volatility does not diverge to infinity (iv) negative and positive price shocks tend to have different impacts on volatility (leverage effect) (v) heavy-tailed, non-gausian distribution
Historical Volatility
Most straightforward way to measure volatility is to estimate time-series of variance on "rolling samples" For zero-mean variable (let us say return), this would be:
2 2 2 s2 = Irt-1 + rt-2 + ... + rt-q M q t
, where q is the latest observation used. This method may produce abrupt changes in estimates.
Exponential volatility
Alternatively, exponential moving average (EMA) estimator of volatility can be used. It uses all data points, and recent observations carry larger weights. (weights are exponentially decreasing).
2 s2 = H1 - lL rt-1 + ls2 , t t-1
where initial value could be unconditional variance in a historical sample. In most financial applications, l=0.94 is used.
Example on S&P 500 index data (change ticker in the code to get other data)
Note that characteristics of volatility can be observed from returns of S&P 500. Moreover, ACF plot suggests us, that returns are not serially correlated, but ACF plot of squared returns shows, that they are not independent. By modeling volatility, we will attempt to capture this kind of dependece.
QF_I_Lecture4.cdf
Prices
1500 1000 500 0
1980
1990
2000
2010
Returns
0.10 0.05 0.00 -0.05 -0.10 -0.15 -0.20 1980 1990 2000 2010
ACF of r
0.2 0.1 0.0 -0.1 -0.2
10
15
20
25
30
ACF of r2
0.2 0.1 0.0 -0.1 -0.2
10
15
20
25
30
Conditional Standard Deviation estimated by EMA (or EWMA)
S&P standard deviation estimate with EMA Hl=0.9L
0.08
0.06
0.04
0.02
0.00
1980
1990
2000
QF_I_Lecture4.cdf
Conditional Heteroscedastic Models
Log returns of an asset at time is either serially uncorrelated, or with minor lower order serial correlations, but it is dependent. Conditional heteroscedastic models are used for modeling s2 as an volatility estimate t by "allowing" heteroscedasticity (time-variation) and capturing that dependence.
ARCH(1)
The first model that provides a systematic framework for volatility modeling is Autoregressive conditional heteroscedasticity (ARCH) model. ARCH(1) model is most common from ARCH(m) models in financial theory. Basic idea is that the mean-corrected return is serially uncorrelated, but dependent, and that the dependence can be described by a simple function of lagged values: at = st et s2 = a0 + a1 a2 t t-1 Adding the assumption of normality, the model can be expressed in terms of information set available in time t: Ft (Engle 1982), (i.e. et is conditionally normally distributed) yt Ft-1 ~ NH0, ht L 2 ht = a0 + a1 yt-1 Example of other notation: yt = c + et st et ~ NH0, 1L s2 = a0 + a1 s2 , t t-1 where a0 > 0, a1 0. Unconditional mean of at is zero, unconditional variance is a0 H1 - a1 L, process is stationary, if a1 < 1, the fourth moment is finite if 3 a2 < 1. 1 Thus excess kurtosis is positive and the tail distribution of at is heavier than normal distribution.
Kurtosis of ARCH(1) processes
The fourth moment of ARCH(1) process: EAet 4 E =
3 a0 2 H1-a1 L
2
1-a1 2 1-3 a1 2
, with 3 a1 2 < 1 r3
kurtHet L =
EAet 4 E EAet E
2 2
=3
1-a1 2 1-3 a1 2
QF_I_Lecture4.cdf
Example : a1 = 0.1
Example : a1 = 0.4
Example : a1 = 0.5
QF_I_Lecture4.cdf
Example : a1 = 0.9
Examples of ARCH(1) artificial processes
Sample ARCHH1L
ARCHH1L volatility
ACF function of a2 t
PACF function of a2 t
a0 a1
0.82 0.823
New Random Case
10
-5
-10
100
200
300
400
500
Example - Simulation of ARCH process ARCH(m)
at = st et , s2 = a0 + a1 a2 + ... + am a2 , t t-1 t-m where at is mean corrected return at = rt - mt , {et < is i.i.d random variables with zero mean and variance 1, somteimes denoted as h - innovations, a > 0, a 0 for i > 0.
QF_I_Lecture4.cdf
at = st et , s2 = a0 + a1 a2 + ... + am a2 , t t-1 t-m where at is mean corrected return at = rt - mt , {et < is i.i.d random variables with zero mean and variance 1, somteimes denoted as ht - innovations, a0 > 0, ai 0 for i > 0. One can easily observe, that large past squared shocks 9a2 =i=1 imply large conditional variance s2 , or t-i t volatility. Thus under ARCH, large shocks tend to be followed by large shocks - ARCH effect
m
Examples of ARCH(m) artificial processes
Note that you have to input a0 > 0, ai 0 for i > 0. in form 8a0 , a1 ..., am <
Input Parameters of ARCHHmL:
am 80.5, 0.1<
Sample ARCHHmL
ARCHHmL volatility
ACF function of a2 t
PACF function of a2 t
New Random Case
0.4
0.2
0.0
-0.2
-0.4 0 5 10 15 20 25 30
Test for ARCH effects in time series
We use Lagrange Multiplier test (LM test), with the null hypothesis of no ARCH effects:
2 2 et = a0 + Is=1 as et-s M + nt q
H0 : a1 =. .. = as = 0 LM = N.R2 ~ c2 HpL
QF_I_Lecture4.cdf
Forecasting with ARCH
Forecasts of the ARCH can be obtained recursively at origin h, the 1-step ahead forecast of s2 is: h+1 s2 H1L = a0 + a1 e2 + ... + am e2 h h h+1-m l-step ahead forecast will be: s2 HlL = a0 + m ai s2 Hl - iL, h i=1 h where s2 Hl - iL = e2 h h+l-i if l - i 0.
Weaknesses of ARCH Models
ARCH model has also following weaknesses: (i) assumes that positive and negative shocks have the same effect on volatility, but empirical testing shows, that assets respond differently to positive and negative shocks. (ii) model gives us description of the conditional variance, but does not explain the real behavior and source of variance (iii) ARCH models tend to overpredict the volatility as they respond slowly to large isolated shocks.
GARCH models GARCH(m,s)
As ARCH model requires many parameters to adequately describe volatility process of returns, extension is used - Generalized autoregressive conditional heteroscedasticity (GARCH) model. It is assumed, that mean equation is adequately described by ARMA, letting at = rt - mt be the mean-corrected log return, GARCH(m,s) model is described by following equation: at = st et , s2 = a0 + m ai a2 + s b j s2 j , t i=1 t-i j=1 twhere {et < is i.i.d random variables with zero mean and variance 1, a0 > 0, ai 0, b j 0, and Hai + bi L < 1, so unconditional variance of at is finite, whereas its conditional variance s2 evolves i=1 t over time. Note, that GARCH model reduces to a pure ARCH(m) model for s = 0.
maxHm,sL
QF_I_Lecture4.cdf
Example GARCH(m,s) artificial processes
Sample GARCHH1,1L
GARCHH1,1L volatility
ACF function of a2 t
PACF function of a2 t
am bs
80.1, 0.2, 0.3< 80.05, 0.2<
New Random Case
Export Simulated Series
1.5
1.0
0.5
0.0 0 100 200 300 400 500
GARCH(1,1)
GARCH(1,1) is most common for financial applications, as the dependencies are mostly very weak. It takes form of: at = st et , s2 = a0 + ai a2 + b1 s2 , t t-1 t-1 where Ha1 + b2 L < 1. Large past shocks of return and volatility in t-1 gives large shocks to volatility in time t, thus volatility clustering is quite well captured.
Example GARCH(1,1) artificial processes
Note that condtition i=1 Hai + bi L < 1 must be met. Initial values are set to simulate GARCH(1,1) process with a0 = 0.5, a1 = 0.2, b1 = 0.4
maxHm,sL
QF_I_Lecture4.cdf
Sample GARCHH1,1L
GARCHH1,1L volatility
ACF function of a2 t
PACF function of a2 t
a0 a1 b1
0.581 0.667 0.296
New Random Case
Export Simulated Series
10
-5
-10
100
200
300
400
500
GARCH-M model
The return of a security may sometimes depend directly on volatility. To model this, we use GARCH in mean (GARCH-M) model. GARCH(1,1) - M is formalized as: rt = m + cs2 + at t at = st et , s2 = a0 + ai a2 + b1 s2 , t t-1 t-1
where m and c are constant. c is also called risk premium
Example GARCH(1,1)-M artificial processes
Note, that with positive risk premium c, returns are positively skewed, as they are positively related to its past volatility
10
QF_I_Lecture4.cdf
Sample GARCHH1,1L-M
ACF function of a2 t
PACF function of a2 t
risk premium c a0 a1 b1
-0.375 0.5 0.38 0.318
New Random Case
Export Simulated Series
-2
-4
100
200
300
400
500
ARIMA-GARCH Models
Common way to build ARCH model is to remove any linear dependencies in the data (i.e.) by ARMA model - for most series, we remove also sample mean from the data.), and use residuals for testing the ARCH effects. This can be done either using Ljung-Box statistics, or ACF, PACF functions, or by Lagrange multiplier test (LM test). If the statistic is significant, then conditional heteroscedasticity of at is detected, and PACF of a2 is used to determine order of ARCH effect. For GARCH, it is not so easy to determine the t order, but empirical findings can serve again, that in most financial applications, we use lower order models such as GARCH(1,1), GARCH(2,1).
QF_I_Lecture4.cdf
11
Example ARIMA(p,d)-GARCH(1,1) artificial processes
Sample ARIMAHp,d,qL-GARCHH1,1L
ACF
ARIMA@p,q,dD parameters
process is unit-root stationary
10 difference ARHpL parameters MAHqL parameters 80.9, -0.4< 80.1, 0.5<
GARCH@1,1D parameters
a0
-5 a1 -10 0 100 200 300 400 500 New Random Case b1
Export Simulated Series
IGARCH - Integrated GARCH
IGARCH models are unit-root (integrated) GARCH models, their key feature is, that past squared shocks is persistent. IGARCH(1,1) is formalized as: at = st et , s2 = a0 + b1 s2 + H1 - b1 L a2 t t-1 t-1
12
QF_I_Lecture4.cdf
Example IGARCH(1,1) artificial processes
IGARCHH1,1L
Simulated series Simulated Volatility
a0 b1
0.611 0.6
New Random Case
Export Simulated Series
800
600
400
200
0 0 100 200 300 400 500
Stochastic Volatility Model
rt = mt + et , et = gIs2 M ht , t s2 = a0 + a1 s2 + nt , t t-1 where 8ht < ~ iidH0, 1L, 8nt < ~ iidI0, s2 M n
Empirical example
Homework #4
Deadline: Tue 15.10.2010, 3:00 pm
Homework may be returned in class, or sent via email to vachal@utia.cas.cz
:] Exercise 1 [:
Estimate ARMA-(G)ARCH model on the real stock market data (use dataset which contains (G)ARCH effect).
QF_I_Lecture4.cdf
13
:] Exercise 1 [:
Estimate ARMA-(G)ARCH model on the real stock market data (use dataset which contains (G)ARCH effect). * Please include your computations program with your results.
Das könnte Ihnen auch gefallen
- GARCH TutorialDokument12 SeitenGARCH TutorialMuhammad MansoorNoch keine Bewertungen
- GARCH Models: Structure, Statistical Inference and Financial ApplicationsVon EverandGARCH Models: Structure, Statistical Inference and Financial ApplicationsBewertung: 5 von 5 Sternen5/5 (1)
- Chapter 3Dokument25 SeitenChapter 3Jose C Beraun TapiaNoch keine Bewertungen
- Time Varying Risk GARCH Models-Part1Dokument31 SeitenTime Varying Risk GARCH Models-Part1knightbtwNoch keine Bewertungen
- The Spectral Theory of Toeplitz Operators. (AM-99), Volume 99Von EverandThe Spectral Theory of Toeplitz Operators. (AM-99), Volume 99Noch keine Bewertungen
- Autoregressive Conditional Heteroskedasticity (ARCH) : Volatility ClusteringDokument9 SeitenAutoregressive Conditional Heteroskedasticity (ARCH) : Volatility ClusteringLyana ZainolNoch keine Bewertungen
- Prsentationmodle GARCHavec RenglishDokument21 SeitenPrsentationmodle GARCHavec Renglishki_soewarsonoNoch keine Bewertungen
- Modelling Volatility in Financial Time Series: An Introduction To ArchDokument16 SeitenModelling Volatility in Financial Time Series: An Introduction To Archlars32madsenNoch keine Bewertungen
- Arch Model and Time-Varying VolatilityDokument17 SeitenArch Model and Time-Varying VolatilityJorge Vega RodríguezNoch keine Bewertungen
- Arch ModelsDokument13 SeitenArch Modelsgarym28Noch keine Bewertungen
- Chapter 4Dokument19 SeitenChapter 4Jose C Beraun TapiaNoch keine Bewertungen
- ARIMA (P, D, Q) ModelDokument4 SeitenARIMA (P, D, Q) ModelselamitspNoch keine Bewertungen
- The Structure of Economics 1Dokument36 SeitenThe Structure of Economics 1José Luis Castillo B100% (5)
- Threshold Heteroskedastic Models: Jean-Michel ZakoianDokument25 SeitenThreshold Heteroskedastic Models: Jean-Michel ZakoianLuis Bautista0% (1)
- Time Series Analysis Exercises: Universität PotsdamDokument30 SeitenTime Series Analysis Exercises: Universität PotsdamSD100% (1)
- Problem Set 4: Sergi Quintana, Joseph Emmens, Ignasi Merediz Sol'a - Econometrics II May 16, 2020Dokument12 SeitenProblem Set 4: Sergi Quintana, Joseph Emmens, Ignasi Merediz Sol'a - Econometrics II May 16, 2020Joe EmmentalNoch keine Bewertungen
- EViews LabDokument13 SeitenEViews LabZakia ShaheenNoch keine Bewertungen
- Financial Time Series ModelsDokument11 SeitenFinancial Time Series ModelsAbdi HiirNoch keine Bewertungen
- Seminsr GarchDokument14 SeitenSeminsr GarchHDNoch keine Bewertungen
- Ei2005 41Dokument17 SeitenEi2005 41siti hayatiNoch keine Bewertungen
- Stationary ProcessDokument178 SeitenStationary ProcessMohamed AsimNoch keine Bewertungen
- Better Hedge Ratios For Pairs TradingDokument11 SeitenBetter Hedge Ratios For Pairs TradingAlex AleksicNoch keine Bewertungen
- Asymmetric GARCHDokument2 SeitenAsymmetric GARCHfazalulbasit9796Noch keine Bewertungen
- Comparison of ARCH Family ModelsDokument4 SeitenComparison of ARCH Family ModelsTalhaNoch keine Bewertungen
- Arch Garch Models StatDokument4 SeitenArch Garch Models StatAyush choudharyNoch keine Bewertungen
- Arch Models and Conditional Volatility: 1, Write The Series As 1)Dokument8 SeitenArch Models and Conditional Volatility: 1, Write The Series As 1)Yusheel RamruthenNoch keine Bewertungen
- STAT758: Final ProjectDokument19 SeitenSTAT758: Final ProjectYeswanthNoch keine Bewertungen
- Introductory Econometrics For Finance Chris Brooks Solutions To Review Questions - Chapter 9Dokument11 SeitenIntroductory Econometrics For Finance Chris Brooks Solutions To Review Questions - Chapter 9Huyền my lifeNoch keine Bewertungen
- HMM TutorialDokument7 SeitenHMM Tutoriallou_ferrigno00Noch keine Bewertungen
- ARIMA GARCH Spectral AnalysisDokument32 SeitenARIMA GARCH Spectral AnalysisRewa ShankarNoch keine Bewertungen
- Estimation and Testing For Arch and GarchDokument9 SeitenEstimation and Testing For Arch and GarchKhalid LatifNoch keine Bewertungen
- CHP 13 ARMADokument23 SeitenCHP 13 ARMASayed AamirNoch keine Bewertungen
- GARCH Model Selena, AnaDokument15 SeitenGARCH Model Selena, AnaSelenaBelikovNoch keine Bewertungen
- Sargent T., Et. Al (2010) - Practicing DynareDokument66 SeitenSargent T., Et. Al (2010) - Practicing DynareMiguel Ataurima ArellanoNoch keine Bewertungen
- A Tutorial On Preview Control SystemsDokument6 SeitenA Tutorial On Preview Control SystemsjaquetonaNoch keine Bewertungen
- Estimating Stock Market Volatility With Markov Regime-Switching GARCH ModelsDokument11 SeitenEstimating Stock Market Volatility With Markov Regime-Switching GARCH ModelseduardohortaNoch keine Bewertungen
- ARCH and GARCH Estimation: Dr. Chen, Jo-HuiDokument39 SeitenARCH and GARCH Estimation: Dr. Chen, Jo-HuiSalman Zia100% (1)
- Financial Time SeriesDokument10 SeitenFinancial Time SeriesIoanaNoch keine Bewertungen
- Process Control: Version 2 EE IIT, Kharagpur 1Dokument12 SeitenProcess Control: Version 2 EE IIT, Kharagpur 1poiuyNoch keine Bewertungen
- Lec4 17Dokument22 SeitenLec4 17RajulNoch keine Bewertungen
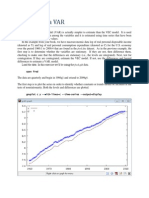
- Estimating A VAR - GretlDokument9 SeitenEstimating A VAR - Gretlkaddour7108Noch keine Bewertungen
- Pulse-Width Modulated D.c.-D.c. ConvertersDokument26 SeitenPulse-Width Modulated D.c.-D.c. ConvertersDeepak NayakNoch keine Bewertungen
- C3-2016 GJPAM Vol. 12 No 2 Pp. 1201-1210Dokument10 SeitenC3-2016 GJPAM Vol. 12 No 2 Pp. 1201-1210julia wulandariNoch keine Bewertungen
- Identification and Estimation - OxfordDokument28 SeitenIdentification and Estimation - OxfordAnimesh Kumar JhaNoch keine Bewertungen
- Chapter 5Dokument20 SeitenChapter 5Ana PereiraNoch keine Bewertungen
- Stata Lab4 2023Dokument36 SeitenStata Lab4 2023Aadhav JayarajNoch keine Bewertungen
- Notes On ARIMA Modelling: Brian Borchers November 22, 2002Dokument19 SeitenNotes On ARIMA Modelling: Brian Borchers November 22, 2002Daryl ChinNoch keine Bewertungen
- Autoregressive Conditional Heteroskedasticity (ARCH) Models: Econometrics IIDokument49 SeitenAutoregressive Conditional Heteroskedasticity (ARCH) Models: Econometrics IIFaizus Saquib ChowdhuryNoch keine Bewertungen
- Arima Modeling With R ListendataDokument12 SeitenArima Modeling With R ListendataHarshalKolhatkarNoch keine Bewertungen
- International Journal of Pure and Applied Mathematics No. 3 2013, 583-592Dokument10 SeitenInternational Journal of Pure and Applied Mathematics No. 3 2013, 583-592Murtadho 108Noch keine Bewertungen
- Arch and GarchDokument39 SeitenArch and GarchJovan NjegićNoch keine Bewertungen
- 0910sem2 ST5209Dokument8 Seiten0910sem2 ST5209jiashengroxNoch keine Bewertungen
- 2.2 Vector Autoregression (VAR) : M y T 1, - . - , TDokument24 Seiten2.2 Vector Autoregression (VAR) : M y T 1, - . - , TrunawayyyNoch keine Bewertungen
- Use, Tsset, Line Generate, Line, Arch, Mgarch, Tsset, Estat IcDokument10 SeitenUse, Tsset, Line Generate, Line, Arch, Mgarch, Tsset, Estat Ic薛璐Noch keine Bewertungen
- David A. Dickey, North Carolina State Univ., Raleigh, NC: Case Studies in Time SeriesDokument9 SeitenDavid A. Dickey, North Carolina State Univ., Raleigh, NC: Case Studies in Time SeriesAshish PandeyNoch keine Bewertungen
- Applied Financial EconomicsDokument17 SeitenApplied Financial EconomicsjeffNoch keine Bewertungen
- 4) (G) ArchDokument62 Seiten4) (G) ArchDunsScotoNoch keine Bewertungen
- Using Eviews To Construct An ARDL Bound Test Part 2Dokument9 SeitenUsing Eviews To Construct An ARDL Bound Test Part 2ashraflotfeyNoch keine Bewertungen
- Calculus Final Test 2017 - 2018 Semester 1Dokument2 SeitenCalculus Final Test 2017 - 2018 Semester 1Hoàng HàNoch keine Bewertungen
- Computational Intelligence (CS3030/CS3031) : School of Computer Engineering, KIIT-DU, BBS-24, IndiaDokument2 SeitenComputational Intelligence (CS3030/CS3031) : School of Computer Engineering, KIIT-DU, BBS-24, IndiaRaju KumarNoch keine Bewertungen
- Prospeccion Geoelec Trica en Corrien Te Continua. Ernest0 Orellana. ParaninfoDokument2 SeitenProspeccion Geoelec Trica en Corrien Te Continua. Ernest0 Orellana. ParaninfoGustavo MiguelNoch keine Bewertungen
- FMEA Minus The Pain FiguresDokument3 SeitenFMEA Minus The Pain FiguresMUNISNoch keine Bewertungen
- 2 EEE - EPM412 Load CCs 2Dokument30 Seiten2 EEE - EPM412 Load CCs 2Mohamed CHINANoch keine Bewertungen
- Integrals of Differential Binomials and Chebyshev's CriterionDokument4 SeitenIntegrals of Differential Binomials and Chebyshev's CriterionEnrique GonzalezNoch keine Bewertungen
- Graphology PDFDokument5 SeitenGraphology PDFpuneeth87Noch keine Bewertungen
- Types of Relation 1Dokument17 SeitenTypes of Relation 1Justin Adrian BautistaNoch keine Bewertungen
- Extraction and Leaching 93851 - 14 ADokument18 SeitenExtraction and Leaching 93851 - 14 Aakarcz6731Noch keine Bewertungen
- PTM Phy F.4.Ch.2.4Dokument13 SeitenPTM Phy F.4.Ch.2.4Bazil BoliaNoch keine Bewertungen
- Ch-1 Measurement (Complete)Dokument13 SeitenCh-1 Measurement (Complete)Mahendra ModiNoch keine Bewertungen
- Failure Rate Modeling Using Equipment Inspection Data: Richard E. Brown (SM)Dokument8 SeitenFailure Rate Modeling Using Equipment Inspection Data: Richard E. Brown (SM)Jackie AcuñaNoch keine Bewertungen
- Beam Deflection - Moment Area Method PDFDokument10 SeitenBeam Deflection - Moment Area Method PDFنور عليNoch keine Bewertungen
- Climate WorkbookDokument119 SeitenClimate WorkbookreaderdarkeyeNoch keine Bewertungen
- 2018-IPS Endterm SolsDokument14 Seiten2018-IPS Endterm SolsAnurag BhartiNoch keine Bewertungen
- 0606 s14 QP 22Dokument16 Seiten0606 s14 QP 22AKRAMNoch keine Bewertungen
- Heat Transfer Lab: Me8512-Thermal Engineering LabDokument55 SeitenHeat Transfer Lab: Me8512-Thermal Engineering LabVinoNoch keine Bewertungen
- Variables Answers ReasonsDokument4 SeitenVariables Answers ReasonsEDEN FE D. QUIAPONoch keine Bewertungen
- Inductive and Deductive ReasoningDokument37 SeitenInductive and Deductive ReasoningGadela KevinNoch keine Bewertungen
- Geometry Class 6 Final ExamDokument4 SeitenGeometry Class 6 Final ExamTanzimNoch keine Bewertungen
- Spe 163492 Pa PDFDokument17 SeitenSpe 163492 Pa PDFsanty222Noch keine Bewertungen
- Attribution ModelsDokument7 SeitenAttribution Modelsjade1986Noch keine Bewertungen
- Chapter 3 - Measure of Location and DispersionDokument11 SeitenChapter 3 - Measure of Location and DispersionNelly MalatjiNoch keine Bewertungen
- 5 - RegressionDokument63 Seiten5 - RegressionMarcello RossiNoch keine Bewertungen
- MA2401 Lecture NotesDokument270 SeitenMA2401 Lecture NotesJojo LomoNoch keine Bewertungen
- 13-Case and Switch VS IfDokument16 Seiten13-Case and Switch VS IfAngel CruzNoch keine Bewertungen
- 06 - Class 06 - Trade SetupsDokument12 Seiten06 - Class 06 - Trade SetupsChandler BingNoch keine Bewertungen
- James Bird Centrality and The Cities Chapters 2-4Dokument28 SeitenJames Bird Centrality and The Cities Chapters 2-4Humberto DelgadoNoch keine Bewertungen
- Gaussian Beam OpticsDokument16 SeitenGaussian Beam OpticsModyKing99Noch keine Bewertungen
- Modeling of Dissolution DataDokument39 SeitenModeling of Dissolution DataanupnakatNoch keine Bewertungen
- Generative AI: The Insights You Need from Harvard Business ReviewVon EverandGenerative AI: The Insights You Need from Harvard Business ReviewBewertung: 4.5 von 5 Sternen4.5/5 (2)
- ChatGPT Side Hustles 2024 - Unlock the Digital Goldmine and Get AI Working for You Fast with More Than 85 Side Hustle Ideas to Boost Passive Income, Create New Cash Flow, and Get Ahead of the CurveVon EverandChatGPT Side Hustles 2024 - Unlock the Digital Goldmine and Get AI Working for You Fast with More Than 85 Side Hustle Ideas to Boost Passive Income, Create New Cash Flow, and Get Ahead of the CurveNoch keine Bewertungen
- Scary Smart: The Future of Artificial Intelligence and How You Can Save Our WorldVon EverandScary Smart: The Future of Artificial Intelligence and How You Can Save Our WorldBewertung: 4.5 von 5 Sternen4.5/5 (55)
- The Digital Mind: How Science is Redefining HumanityVon EverandThe Digital Mind: How Science is Redefining HumanityBewertung: 4.5 von 5 Sternen4.5/5 (2)
- Working with AI: Real Stories of Human-Machine Collaboration (Management on the Cutting Edge)Von EverandWorking with AI: Real Stories of Human-Machine Collaboration (Management on the Cutting Edge)Bewertung: 5 von 5 Sternen5/5 (5)
- ChatGPT Money Machine 2024 - The Ultimate Chatbot Cheat Sheet to Go From Clueless Noob to Prompt Prodigy Fast! Complete AI Beginner’s Course to Catch the GPT Gold Rush Before It Leaves You BehindVon EverandChatGPT Money Machine 2024 - The Ultimate Chatbot Cheat Sheet to Go From Clueless Noob to Prompt Prodigy Fast! Complete AI Beginner’s Course to Catch the GPT Gold Rush Before It Leaves You BehindNoch keine Bewertungen
- The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our WorldVon EverandThe Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our WorldBewertung: 4.5 von 5 Sternen4.5/5 (107)
- Four Battlegrounds: Power in the Age of Artificial IntelligenceVon EverandFour Battlegrounds: Power in the Age of Artificial IntelligenceBewertung: 5 von 5 Sternen5/5 (5)
- 100M Offers Made Easy: Create Your Own Irresistible Offers by Turning ChatGPT into Alex HormoziVon Everand100M Offers Made Easy: Create Your Own Irresistible Offers by Turning ChatGPT into Alex HormoziNoch keine Bewertungen
- HBR's 10 Must Reads on AI, Analytics, and the New Machine AgeVon EverandHBR's 10 Must Reads on AI, Analytics, and the New Machine AgeBewertung: 4.5 von 5 Sternen4.5/5 (69)
- Artificial Intelligence & Generative AI for Beginners: The Complete GuideVon EverandArtificial Intelligence & Generative AI for Beginners: The Complete GuideBewertung: 5 von 5 Sternen5/5 (1)
- The AI Advantage: How to Put the Artificial Intelligence Revolution to WorkVon EverandThe AI Advantage: How to Put the Artificial Intelligence Revolution to WorkBewertung: 4 von 5 Sternen4/5 (7)
- T-Minus AI: Humanity's Countdown to Artificial Intelligence and the New Pursuit of Global PowerVon EverandT-Minus AI: Humanity's Countdown to Artificial Intelligence and the New Pursuit of Global PowerBewertung: 4 von 5 Sternen4/5 (4)
- Python Machine Learning - Third Edition: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow 2, 3rd EditionVon EverandPython Machine Learning - Third Edition: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow 2, 3rd EditionBewertung: 5 von 5 Sternen5/5 (2)
- Artificial Intelligence: The Insights You Need from Harvard Business ReviewVon EverandArtificial Intelligence: The Insights You Need from Harvard Business ReviewBewertung: 4.5 von 5 Sternen4.5/5 (104)
- Your AI Survival Guide: Scraped Knees, Bruised Elbows, and Lessons Learned from Real-World AI DeploymentsVon EverandYour AI Survival Guide: Scraped Knees, Bruised Elbows, and Lessons Learned from Real-World AI DeploymentsNoch keine Bewertungen
- Artificial Intelligence: A Guide for Thinking HumansVon EverandArtificial Intelligence: A Guide for Thinking HumansBewertung: 4.5 von 5 Sternen4.5/5 (30)
- Architects of Intelligence: The truth about AI from the people building itVon EverandArchitects of Intelligence: The truth about AI from the people building itBewertung: 4.5 von 5 Sternen4.5/5 (21)
- ChatGPT Millionaire 2024 - Bot-Driven Side Hustles, Prompt Engineering Shortcut Secrets, and Automated Income Streams that Print Money While You Sleep. The Ultimate Beginner’s Guide for AI BusinessVon EverandChatGPT Millionaire 2024 - Bot-Driven Side Hustles, Prompt Engineering Shortcut Secrets, and Automated Income Streams that Print Money While You Sleep. The Ultimate Beginner’s Guide for AI BusinessNoch keine Bewertungen
- The Roadmap to AI Mastery: A Guide to Building and Scaling ProjectsVon EverandThe Roadmap to AI Mastery: A Guide to Building and Scaling ProjectsNoch keine Bewertungen
- How To: GPT-4 for Financial Freedom: The Entrepreneur's Guide to Thriving in the AI EraVon EverandHow To: GPT-4 for Financial Freedom: The Entrepreneur's Guide to Thriving in the AI EraBewertung: 4 von 5 Sternen4/5 (9)
- Mastering Large Language Models: Advanced techniques, applications, cutting-edge methods, and top LLMs (English Edition)Von EverandMastering Large Language Models: Advanced techniques, applications, cutting-edge methods, and top LLMs (English Edition)Noch keine Bewertungen
- Who's Afraid of AI?: Fear and Promise in the Age of Thinking MachinesVon EverandWho's Afraid of AI?: Fear and Promise in the Age of Thinking MachinesBewertung: 4.5 von 5 Sternen4.5/5 (13)