Antiderivative Of CSC

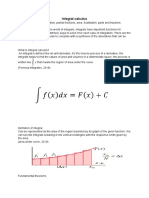
Antiderivative Of CSC The general or most often used formula for a trigonometric function is shown below where sin x is any trigonometric function and cos x is its derivative.

imilar to the integration for sec x, many texts state that to integrate csc x, use the "trick" of multiplying by (csc x - cot x)/(csc x - cot x). This too is the method of someone who already knows the answer. The correct method to do the integration is as follows. Separate the last integral by the method of Partial Fractions: Multiply by the common denominator: A(1 - cos x) + B(1 + cos x) = sin x dx A - A cos x + B + B cos x = sin x dx (A+B) + (B-A)cos x = sin x dx Match like terms on each side of the equation, but which of two possible ways? 2. A+B = 0 and 3. (B-A)cos x = sin x dx
KnowMoreAboutIntegrationWorksheet

Tutorcircle.com

PageNo.:1/4

Solving Initial Value problems in Antiderivatives Antiderivative is the term used in the calculus mathematics and especially in the topic of the Differential Equations. The anti derivatives are the type of the integral equations in which we dont have limits on the Integration symbol. It is the reverse process of the derivatives or we can say it as the process of reverse differentiat. Antiderivative and Indefinite Integrals What anti derivatives are and what are the indefinite integrals in the calculus? We will also go through the relationship between the Antiderivative and indefinite integrals. Lets move to the topic with the introduction of the anti derivatives. The normal Integration is called as the anti derivative. We can also understand the anti derivative. Properties of Integral Integration is important part of Calculus. Let us talk about some properties related to Integration. Fundamental theorem of calculus: If f(x) is continuous on [a,b] then, g(x) = ab f(t) dt And it is differentiable on (a,b) then, g(x) = f(x) Property 1: k f (x) dx = k f(x) dx, where k is any number. Applications of Antiderivatives Anti derivative of function f is the function F whose derivative is function f. We can understand it by an equation as F'=f. This process is also known as anti differentiation. This term is related to the definite integrals by using the functions of calculus. It can be understand by an example as the function F(x)=x3/3 is an anti derivative of the function.

ReadMoreAboutRealNumberDefinition

Tutorcircle.com

PageNo.:2/4

Here a denotes any nonzero constant and c is an integral constant. There is a list of antiderivatives of csc functions which is useful in solving the trigonometric functions. csc ax dx = - 1/a log (csc ax + cot ax ) + c, csc2 ax dx = -cot x + c, cscn ax dx = - csc n-1ax cos ax/a (n-1) + (n-2 / n-1) cscn-2 ax dx, ( for n -1) dx/ (cos x + 1) = x 2. sin (x/2) / cos (x/2) + sin (x/2) + c, dx/ (cos x - 1) = 2. sin (x/2) / cos (x/2) - sin (x/2) - x + c,

Tutorcircle.com

PageNo.:3/4 PageNo.:2/3

ThankYou

TutorCircle.com