223

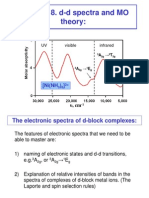
Consider the d-d electronic transitions for Transition Metal Complexes. Before we can do this, we must realize that spectroscopic transitions occur between states and not orbitals. Therefore: We must determine states for various electronic configurations in: 1. Free atoms or ions without a ligand set Term Symbols 2. Complexes in a crystal (or ligand field)

Electronic States and Multiplicities

(rather than orbital states and energies) are Relevant to Electronic Spectroscopy and EPR (Electron Paramagnetic Resonance) Spectroscopy

Free ion states

Free ion

versus
weak field ligands

Orbital States (ligand field)

strong field ligands

Determine term Symbols

to relate the two Determine Electronic use a Tanabe-Sugano States and Multiplicities Diagram

224

Free ions can be described by Term Symbols:

2S + 1

LJ

where: 2S + 1 is spin multiplicity L is Total orbital angular momentum J is the spin, orbit (L + S) coupling If total L = L=0 L=1 L=2 L=3
(Ltotal = l1 + l2 + for each electron)

S symbol P symbol D symbol F symbol

Multiplicity: 2S + 1 is calculated from number of unpaired electrons S = 0 (all paired), S = 1/2 (one u.e.) , S = 1 (2 u.e.) , S = 3/2 (3 u.e.) , etc. Russell-Saunders Coupling: J ranges from L + S, , L-S and all integers in between

225

Ground-State Term Symbols for Any Electronic Configuration: The Ground State has: 1. Choose Maximum L value 2. Choose Maximum S value 3. Choose J value: (a) smallest J value if orbital sub-shell is less than half-filled (b) largest J value if orbital sub-shell is greater than half-filled

226

p2 Lmax = 1 P S=1 2S + 1 = 3 J = L+S .... L-S = 2, 1, 0 use lowest J value for < half-filled and highest J value for greater than half-filled

+1 3

-1

P0

3d3 [Ar] 3d 34s0 Lmax = 3 +2 4 +1 0 -1 -2 Smax = 3/2 F 2S + 1 = 4

F3/2

J = L+S .... L-S =9/2, 7/2, 5/2, 3/2 3/2 use lowest J value for < half-filled and highest J value for greater than half-filled

3d5 Mn2+ ion Lmax = 0 +2 6 +1 0 -1 -2 Smax = 5/2 S 2S + 1 = 6

J = L+S .... L-S =5/2

S5/2

227

Determining Energy States from Orbital Configurations

(after Russell-Saunders Term symbols now what?)

Strong-field Cases (very different than free ions) The ligand field dominates, therefore energy states are determined by the symmetries of the orbitals in which the electrons reside. FIVE cases in determining Electronic States and their spin multiplicities from Electronic Configurations (orbital designations)
Note: orbitals have lower case letters & states have capital letters

Case 1: All orbitals are fully occupied. (a) Multiplicity (2S + 1) with S = 0 (b) electron distribution is totally symmetric
Oh Cr(CO)6 t2g6eg0
1

C4v Co(NH3)5X]2+

A1g

b22e4aa10b10 b1 a1

A1

eg

t2g b2

228

Case 2: Non-degenerate orbital that is singlyoccupied. (a) Multiplicity (S = 1/2): (2S + 1) = 2 or doublet (b) if symmetry of the occupied orbital is X, then the State Symmetry is 2X.
C4v [Co(NH3)5X]+ b22e4aa11b10 b1 a1 e b2
2

A1

Case 3: two singly occupied, non-degenerate orbitals (a) Multiplicity two cases to consider S=0, paired electrons, 2S+1 = 1 or a singlet S=1, two unpaired electrons, 2S+1 = 3 or a triplet (b) State Symmetry is the direct product of the symmetry of the electrons in the two orbitals X1 X2 (these are the representations in the point groups)

229

[Pt(CN)4]2square planar D4h a1g2eg4b2g1b1g1 B2g B1g = A2g (in D4h p.g.) So you get two states:
3

Excited State for a d2 ion t2g1eg1 in Oh T2g x Eg = T2g + T1g

1

T2g, 3T2g, 1T1g, 3T1g

A2g, 1A2g

all spins possible

Question How do you multiply X1 X2, where X1 and X2 are representations in the point group? B2g B1g = ? Answer Multiply the characters (numbers) for the representations in D4h character table

230

Question What if inspection does not work? Then you must reduce the new representation to a sum of certain representations in the group.

you must use the reduction formula: ai = 1/h ( R iR n) ai refers gives you the number of a particular irred. rep. that is contained in the reducible representation 1/h (h is the order of the group = total # of operations)

R = character of the new (reducible representation) iR = character of the irreducible rep. in the group

231

For Oh h = order of group = 48 operations n = varies for each column

example:
Oh A1g E 1 8C3 1 6C2 6 C4 1 1

n = 8 for this class n = 6 for this class

T2g x Eg => reduce using the formula #A1g: 1/48[(6 x 1 x 1) + 0 + 0 + 0 + (-2 x 1 x 3) + (6 x 1 x 1) + 0 + 0 + (-2 x 1 x 3) + 0] [6 6 + 6 6] = 0 #A2g: #Eg: =>0 =>0 1/48[(6 x 3 x 1) + 0 + 0 + 0 + (-2 x 1 x 3) + (6 x 3 x 1) + 0 + 0 + (-2 x -1 x 3) + 0] : 1/48[18 + 0 + 0 + 0 + 6 + 18 + 6] = 1/48[48] = 1

#T1g:

#T2g:

1/48[(6 x 3 x 1) + 0 + 0 + 0 + (-2 x -1 x 3) + (6 x 3 x 1) + 0 + 0 + (-2 x -1 x 3) + 0] = 18 + 6 + 18 + 6 = 1 T2g x Eg = T1g + T2g

Therefore:

232

and since there are two electrons in different orbitals t2g1eg1 => it leads to both singlet and triplet states for both Energy Terms:

T1g 1 T2g

T1g 3 T2g

Case 4: Degenerate orbitals with a hole (lacking 1e- to be filled) (a) hole formalism a degenerate orbital with a hole is equivalent to same degenerate orbital occupied by a single e-. (b) Multiplicity S = 1/2 (2S + 1 = 2) doublet state

e.g. [Ru(bpy)3]3+ => t2g5eg0 2T2g [Mn(CN)6]4- => same

233

Case 5: Two electrons in a degenerate orbital (or nelectrons in a degenerate orbital)

a) state symmetry is given by X X (direct product of the orbital symmetry) b) *multiplicity can be a triplet or a singlet * Problem is matching the correct symmetry to multiplicity! i.e. it must obey the Pauli principle (if 2 electrons have the same spin, they must occupy different orbitals or energy states)

Example in Oh t2g6eg2 Multiply Eg x Eg = ?A1g + ?A2g + ?Eg (the irreducible reps. that arise from Eg x Eg) you must match the symmetry with the multiplicity by lowering the symmetry. use correlation tables
a1g eg KEY IS TO LOWER THE SYMETRY FROM Oh to D4h removes b1g degeneracy

234

You can write two electrons in four different ways in these two orbitals A, B, C1 and C2
a1g b1g B C1 a1g b1g C2

a1g b1g A

a1g b1g

singlet and triplet

METHOD OF DESCENDING SYMMETRY

235

A. In D4h, a1g2 must be a singlet because of the Pauli Principle (if two electrons are in the same orbital, they must have opposite spins). a1g2 is a case 1 situation so state symbol is 1A1g B. In D4h, b1g2 must be a singlet for same reason above. b1g2 is a case 1 situation so state symbol is again 1A1g

C. b1g1a1g1 (triplet)

b1g1a1g1 (singlet)

(both are case 3). Multiply B1g x A1g in D4h point group => reduces to B1g 1 B1g 3B1g Now go to correlation table (p. 437 Cottons Group Theory Book) and find the correspondence between Oh and D4h point groups.

236

Oh
?
?

D4h
___----------------------------------

A2g ? Eg

A1g

?
? ?

B1g A1g ? B1g

1

A1g

D4h 1 A1g
1

We wind up with A1g B1g B1g A1g

These are the three state multiplicities that we are trying to assign. Lowering the symmetry cannot change the multiplicity
1

Oh
1

Eg

B1g B1g A1g

3

3 1

A2g A1g

Example Two: Case 5: Assigning State Terms to Orbital Configurations where 2 electrons are in a degenerate set of orbitals. Oh t2g2 (T2g x T2g) => reducible representation
use mathematical formula to reduce it: you get =>
?

A1g + ?Eg +?T1g +?T2g

237

We must lower the symmetry far enough such that all E (two-dimensional and T (threedimensional) representations become onedimensional (or a sum of one-dimensional) representations. (look at Correlation Table)
We have chosen to go all the way down to C2h (preserves center of symmetry) Oh C2h A1g Eg T1g T2g Ag Ag + Bg Ag + Bg + Bg (Ag + 2Bg) Ag + Ag + Bg (2Ag + Bg)

Now go back to the orbitals:

There are six different ways that two e- can go into these orbitals in a C2h point group orbital diagram:
bg ag2 ag1 1 *2 bg ag2 ag1 *3 bg ag2 ag1 4 bg ag2 ag1 *5 bg ag2 ag1 6 bg ag2 ag1

*These have singlet versions as well as the triplets shown here

238

Now, we must determine the states corresponding to these orbital configurations. (all of these can be solved by inspection of character table) (1)* ag1 ag1 = Ag (2) ag1 ag2 = Ag (3) ag1 bg = Bg (4)* ag2 ag2 = Ag (5) ag1 bg = Bg (6)* bg bg = Ag (1)*, (4)*, (6)* must be singlets because the electrons are in the same orbital => 1Ag, 1Ag, 1Ag (2), (3), (5) can be both singlets and triplets => 1Ag, 3Ag 1Bg, 3Bg 1Bg, 3Bg to summarize (1) 1Ag (2) 1Ag 3Ag (3) 1Bg 3Bg (4) 1Ag (5) 1Bg 3Bg (6) 1Ag Remember, we had earlier determined that T2g x T2g = ?T2g + ?T1g + ?Eg + ?A1g and T2g = 2Ag + Bg T1g = Ag + 2Bg Eg = Ag + Bg A1g = Ag

239

Now make the correlation:

Oh
1

C2h
1 1

Make the connections from

Ag Eg T2 g

Ag

lower symmetry on the right hand side to her higher symmetry on the left. The correlations are unique- this is the only way that it would work. The two triplet 3Bg 's must go with
T1g because there is only one 3A g

Ag

1 1 1

Bg

Ag Bg

Ag

1 3 3

T1g

Bg Bg Ag

to go with them

240

Two extremes of considering significance of L-S or spin-orbit coupling: L-S coupling is the coupling of the magnetic dipole of electron spin moment with the orbital moment
1. Russell-Saunders in this scheme e-/e- repulsion dominates and spin-orbit coupling (L-S) coupling is treated as a perturbation on e-/e- repulsion. L-S coupling is small with first row T-metals (second row also). 2. j-j coupling in this scheme, the L-S coupling dominates and maximum J values are used to describe states and e-/e- repulsion is a perturbation on these states. Third row T-metals and rare earth elements must be treated in this way.

241

242

How do you get ordering of these? Consider e-/e- repulsions as being important (as before in free ions) How would you connect the Free ions to the strong-field cases? i.e. take Russell-Saunders Term symbols into orbital-based states without derivation Correlation of => Free ion RS States (L=0) (L=1) (L=2) (L=3) (L=4) S P D F G => => => => => Energy States of Orbital A1 T1 E + T2 A2 + T1 + T2 E + T1 + T2 + A1

Tanabe-Sugano Diagrams use lines to connect free ion states to molecular states.