Beruflich Dokumente
Kultur Dokumente
A Study of The Flow Field of A Confined and Submerged Impinging Jet
Hochgeladen von
EKKACHAI PRABNAKORNOriginalbeschreibung:
Originaltitel
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
A Study of The Flow Field of A Confined and Submerged Impinging Jet
Hochgeladen von
EKKACHAI PRABNAKORNCopyright:
Verfügbare Formate
Pergamonl
1~. 3. Heat Mars Trmsfer. Vol. 41, Nos 8-9, pp. 1025-1034, 1998 iQ 1997 Elsevier Science Ltd. All rights reserved Printed in Great Britain 0017-9310/98 $19.00+0.00
PI1 : soo17-931q97)00205-6
A st,udy of the flow field of a confined and submerged impinging jet
JANICE A. FITZGERALD and SURESH V. GARIMELLA?
Department of Mechanical Engineering, University of Wisconsin-Milwaukee, Milwaukee, Wisconsin 53201, U.S.A.
(Received 18 March 1997 and infinalform 3 July 1997)
P.O. Box 784,
Abstract--The flow field of an axisymmetric, confined and submerged turbulent jet impinging normally on a flat plate was studied experimentally using laser-Doppler velocimetry. Single jets of a perfluorinated dielectric liquid (FC-77) issuing from square-edged, geometrically similar nozzles were used in the experiments with the radial outflow confined between parallel plates. The nozzle (length to diameter) aspect ratio was unity, giving rise to a still-developing velocity protile at the nozzle exit. Experiments were conducted with nozzle diameters of 3.18 and 6.35 mm, nozzle-to-target plate spacings of up to four jet diameters, and Reynolds numbers in the range of 850&23,000. The toroidal recirculation pattern in the outflow region characteristic of confined jets is mapped. Velocities and turbulence levels are presented over a fine measurement grid in the pre-impingement and wall-jet regions. 0 1997 Elsevier Science Ltd.
INTRODUCTION
Impinging jets are used in many heat and mass transfer applications because of their effective transport capabilities. Applica.tions include turbine-blade cooling, paper drying #and electronics packaging. Trends observed in local heat transfer measurements are closely related to the velocities and turbulence levels of the flow field. Experimental and analytical studies of the flow field in free and submerged jets have provided valuable i:nformation regarding their heat transfer characteristics. The presence of a confining topplate facing the target plate in jet impingement, however, results in a more complicated flow structure, and little infomration is available in the literature for this configuration. The purpose of the present study is three-fold : to experimentally investigate the characteristics which are unique to confined and submerged impinging jets ; to contrast these with the flow fields for free-surface and submerged but unconfined jets ; and to interpret the respective heat transfer characteristics in light of the differences in flow fields. Valuable insight into the heat transfer characteristics of free-surface liquid jets [l-3] and air jets [4-81 (submeiged but unconfined) has been gained through the stu of their flow fields, but limited work dy on the effect of confinement in jet impingement has been reported. Investigations of the effect of confinement on heat transfer in air jets [9, lo], planar water jets [l l] and axisymmetric liquid jets of a perfluorinated dielectric fluid [12-151 show a resulting reduction in stagnation-region heat transfer. Flow field measurements in the potential core of an air
7 Author to whom correspondence should be addressed.
jet show that confinement increases the length of the potential core, decreases turbulence levels in the jet, and reduces the stagnation point heat transfer by up to 10% [16]. In general, the heat transfer to impinging jets can be characterized by the jet Reynolds number, fluid Prandtl number, nozzle geometry (diameter, length and shape), and nozzle-to-target plate spacing. Turbulence levels of the jet play an important role in stagnation heat transfer, with higher levels of turbulence resulting in high stagnation heat transfer. Exit levels of turbulence [ 14,9] as well as nozzle geometry [lo, 13, 16, 171 can affect levels of turbulence at the impingement surface. The mean radial velocity gradient of the jet is reported to be more significant to stagnation heat transfer than turbulence levels in fully developed free jets [2, 31. The dimensionless velocity gradient is reported to be largely independent of the Reynolds number and the nozzle diameter. At small nozzle-to-target plate spacings, secondary peaks in the heat transfer distributions have been observed [4, 6, 8,9, 1 l-141. The peaks are more pronounced at small spacings, decreasing in prominence and moving radially away from the jet axis as the spacing increases. Increasing the Reynolds number results in a more pronounced peak, but only slightly affects the location of the peak, moving it away from the jet axis [S, 9, 141. Confinement is reported to increase the magnitude of the secondary peak in heat transfer distribution for liquid jets [ 121, but decreases the magnitude of the peaks in air jets [9]. The peaks are generally understood to result from a transition to turbulence in the wall-jet boundary layer, although in the confined jet it is possible that they may also be due to the recirculation pattern found in the outflow region [ll].
1025
1026
J. A. FITZGERALD
and S. V. GARIMELLA
NOMENCLATURE
d h H k
e NU
Pr r Re
nozzle diameter local heat transfer coefficient distance between nozzle plate and target plate thermal conductivity nozzle length (nozzle-plate thickness) Nusselt number (hd/k) Prandtl number (V/U) radius coordinate with origin at the jet axis Reynolds number (vjd/v) mean component of local radial velocity
Km,
V
0, v, V,, Z
rms of the fluctuating component of local radial velocity mean component of local axial velocity jet centerline velocity jet mean exit velocity rms of the fluctuating component of local axial velocity coordinate along the jet axis with origin at the target plate.
Greek symbols CI thermal diffusivity V kinematic viscosity.
EXPERIMENTAL
SETUP AND
PROCEDURES
The jet impingement facility used in the experiments is a transparent closed-loop system containing a pump, flow meters, and a flow-conditioning plenum at the end of which plates with nozzles of different diameters can be mounted. A jet of FC-77 (a perfluorinated, dielectric liquid with Pr = 25.3, p = 1789 kg me3 and v = 0.86 x lop6 m* SKat 2OC) issues at 20C from the nozzle into a tank of stagnant fluid at the same temperature and impinges on a target plate. Details of the experimental facility are available in [14]. For the present study, nozzle diameters of 6.35 and 3.18 mm were used with the thickness of the nozzle plate equal to the diameter of the nozzle ; a nozzle length-to-diameter aspect ratio (f/d) of one results for both nozzles. The jet velocity profile for this nozzle aspect ratio is neither fully-developed nor uniform, but is still-developing [13]. Nozzle-to-target plate spacings (H/d) of 2, 3 and 4 were studied for each nozzle. The measurements were obtained at three Reynolds numbers (V,d/v) of 8500, 13,000 and 23,000. The confinement region bounded by the nozzle and target plates, which is the domain of focus for this study, as well as the measurement locations, are illustrated in Fig. 1. The velocity and turbulence measurements were obtained with a TSI laser-Doppler velocimeter using a Coherent 2 Watt Argon-ion laser. The 514.5 nm (green) line of the laser was used for both velocity components: the components were measured independently. The focal length of the transmitting lens was 350 mm and the beam spacing was 50 mm. The system is set up in back-scatter mode, with the receiving optics mounted in the same probe as the transmitting optics, and carried by fiber-optic cable to the receiving system where the photomultiplier tubes are located. After the light is converted to an electrical signal and filtered, a TSI model 550 signal processor
converts the data from analog to digital which is then fed to a personal computer for analysis. Frequency shifting was used to accurately determine the negative velocities in the flow. Seed particles of corn starch (N 5 pm diameter) were added to the fluid to provide acceptable data rates. Seven thousand data points were taken at each position to determine the local mean velocity and turbulence level. The averaging was performed over 1000 to 15,000 data points, and the results were found to be independent of sample size for sizes over 5000 data points. The sampling rate varied from approximately 800 to 3000 Hz. A computer-driven, motorized precision traversing system was used to position the measurement volume in the flow field. The traversal resolution in the three directions was f 0.005 mm, with a placement precision of 0.12 mm m- . Before each test, finely-spaced velocities were obtained in perpendicular directions through the jet. The symmetry in the profiles was used to determine the location of the jet axis. The radial (u) and axial (u) velocity components (with respect to the jet axis) were measured in somewhat coarse increments over the entire confined flow-field region to map the recirculation patterns which are a characteristic of the confined nature of the radial outflow. In addition to this mapping of the entire flow field, two sets of more finely spaced measurements were obtained for each configuration (Fig. 1). The axial velocity component was measured in a region centered on the jet axis and extending over a radius of 1.75 nozzle diameters. Obstruction of the laser beams by the nozzle and target plates prevented v-measurements from being obtained in a region very close to these plates. Hence, the v-measurement grid extended in the axial (z) direction to within 4.5 mm of the surfaces as shown in Fig. 1. The radial velocity component was obtained in a non-uniform grid with more measurement loca-
Flow field of an
impinging jet
1027
v measurement mesh u measurement mesh
Fig. 1. Schematic diagram of the experimental impingement configuration and measurement locations for the radial (tf) and the axial (u) velocity components; in addition to these fine meshes, u-u data were obtained in a coarser mesh throughout the flow field.
tions in the region:; of interest : as seen in Fig. 1, the mesh was most dense close to the target plate and near stagnation. The uncertainty in setting the average jet velocity through the rotameters was minimized by calibration and estimated to be 4% at Re = 8500 (for d = 6.35 mm) decreasing to 1% at Re = 23,000 (for d = 3.18 mm). The uncertainty in the velocity measurements obtained using the velocimeter was estimated to be less than 2%.
RESULTS AND DISCUSSION
Velocity and turbulence measurements are presented in this se&on to describe the flow field in the recirculation pattern in the confined outflow, the development of the jet after exiting the nozzle (including the potential core), and the development of the flow along the impingement surface.
Recirculation pattern in the confined outflow
The effect of nozzle-to-target plate spacing on the flow pattern is shown in Fig. 3 for a 6.35 mm nozzle at Re = 8500. Increasing the nozzle-to-target plate spacing also moves the center of the toroid radially outward (from 7.8 d to 9.5 din this case), but its distance from the target plate remains unchanged. These changes to the recirculation pattern in response to changes in both the Reynolds number and the nozzle-to-target plate spacing are consistent with flow visualizations previously obtained for this configuration [14, 151. In jet impingement heat transfer, the presence of the confining top wall would thus cause fluid heated by the target plate to recirculate and become entrained into the impinging jet. This could be a contributing effect in the lower heat transfer coefficients obtained in confined jets relative to the unconfined case.
Pre-impingement jet
A unique feature of submerged and confined jets is the presence of a toroidal recirculation zone in the outflow region. Figure 2 illustrates the recirculation pattern which is a characteristic of the effect of the confining top plate on the flow field. The results are shown at three different Reynolds numbers for a nozzle diameter of 6.35 mm and a nozzle-to-plate spacing (H/d) of 3. The toroid moves radially outward and closer to the target plate as the Reynolds number increases. For the 6.35 mm nozzle at H/d = 3, the center of the toroid moves radially outward from 7.8 d to 9.6 d and from a location 1.4 d from the target plate to 1.2 d away as Re is increased from 8500 to 23,000.
Figure 4(a) shows a typical plot of the velocity profiles (normalized with the mean exit velocity of the jet) in the potential core. The normalized velocity profiles for all three Reynolds numbers tested were similar; Fig. 4(a) is for Re = 8500 and d = 6.35 mm. Close to the nozzle exit, it is seen that the profile is neither uniform nor fully-developed. The velocity profile widens (the jet spreads) as ambient fluid is entrained into the jet. Hrycak et al. [S] described the linear rate of spread of free jets. Measurements in the present study of submerged and confined jets also display linearity in the widening of the jet. The dashed lines in Fig. 4(a) are placed at the position where the axial velocity decreases to 0.05 u,. The dotted lines, placed at 0.95 v,, show the degradation of the potential
1028
J. A. FITZGERALD and S. V. GARIMELLA
Re=8500
Oo
10
11
Re= 13000
d-
. j a
10
.(
11
Re=23000
2
;,
.
13,000and 23,000.
0 1 2 3 4 5r/d 6 7 a lo Fig. 2. Streamlines illustrating the recirculating flow patterns for d = 6.35 mm and H/d = 3 at Re = 8500,
core due to the transfer of momentum across the jet as it widens. From the results, it may be deduced that the potential core is longer than H/d = 4. Since this study deals with confined jet impingement, and physical extent of confinement is fixed, the experiments were restricted to H/d < 4. The effect of confinement on the length of the potential core could thus not be systematically characterized. Turbulence intensities in the potential core for the same case as considered in Fig. 4(a) (d = 6.35 mm, Re = 8500, and H/d = 4) are plotted in Fig. 4(b). Close to the nozzle exit, peaks in turbulence occur at the edges of the nozzle (r/d = 0.5). As the jet develops, the peaks decrease in magnitude as the turbulence diffuses through the jet. By the time the target plate is encountered, the turbulence levels in the figure are seen to have become nearly uniform across the jet. The results also show that the centerline turbulence levels increase with axial distance from the nozzle exit : the centerline turbulence increases for the case in Fig. 4(b) from 10.2% at a location 4.4 mm from the nozzle exit to 16.5%, 21.4 mm away from the exit. These trends in the diffusion of turbulence levels through the
jet as well as the increase of turbulence
levels with distance from the nozzle plate agree with observations for unconfined air jets [4]. It may be recalled that the nozzle aspect ratio of the cases studied results in a still-developing profile at the nozzle exit, and that turbulence levels measured are specific to this nozzle configuration. Figure 5 shows the normalized axial velocity at the jet centerline (Q/Y) as a function of distance from the nozzle exit. The centerline velocity decreases gradually over a distance of 2.5 nozzle diameters from the jet exit. Over the next 1.5 d of distance, as the target plate is approached, the centerline velocity drops rapidly. These results appear to agree with those reported by Gardon and Akfirat [4], that a submerged impinging jet propagates as a free (non-impinging) jet to within a distance of 1.2 nozzle diameters from the impingement surface, at which state it decelerates rapidly. For unsubmerged jets, however, Stevens et al. [2] report that the target plate influences the pre-impingement jet only up to a distance of 0.5 d from the plate. In contrast to the velocities, centerline turbulence levels were shown to increase [17] throughout the devel-
Flow field of an impinging jet
1029
OL--L------L...-l. 0 1
. ~~l ~~ ~.~ ~ ~ 3 4 5
10
11
O~...~~,..................~~.... .~~~,......~...~. 0 1
2 3 4 r?d 6 7 8
10
11
Fig. 3. Streamlines illustrating the recirculating flow patterns for d = 6.35 mm and Re = 8500 for H/d = 3 and H/d = 4.
opment of the jet as the turbulence at the walls of the nozzle as well as that generated subsequently due to shear interactions diffuse to the center of the jet. plate spacing is Therefore, as nozzle-to-target increased, the centerline velocities at the impingement surface are smaller, but turbulence levels are larger than at the nozzle: exit. Heat transfer measurements [ 141 show slightly lmcreasing levels of stagnation Nusd selt number as H, is increased (for H/d < 4), suggesting that turbulence levels are more significant to stagnation Nu than velocities. At small nozzle-to-target plate spacings, diameter alone is seen to affect Nu in the range r/d < 1 19, 13, 171. An increase in nozzle diameter results in significantly higher ;stagnation Nu with all other parameters (Re, Pr, H/d) held constant. A comparison of the two nozzle dia.meters of this study showed higher centerline velocities and turbulence levels (both normalized with jet exit velocity) throughout the development of the larger jet, both conditions contributing to the higher Nu at the stagnation point.
Flow along the impingement surface
Radial-velocity profiles along the target plate show a maximum velocity near the plate for small r/d. Profiles are shown in Fig. 6(a) in the region close to the impingement surface for d = 3.18 mm and H/d = 4 at Re = 23,000. The development of these profiles is further discussed later, in Figs 7 and 8. When the velocities were normalized with the mean jet exit
velocity, no influence of Reynolds number was detectable in the radial velocity protiles. One descriptor of the wall-jet development is the zero-velocity plane separating the region in the flow characterized by radially outward velocities from the region with radially inward flow as shown by the dashed line in Fig. 6(b). The wall-jet development so defined was minimally affected by the size of the nozzle diameter or the Reynolds number. The slope of the zero-velocity plane characterizing the wall-jet development remained nearly constant for all cases, ranging from 0.11 to 0.15. A comparison of the radial velocity profiles at three nozzle-to-target plate spacings is shown in Fig. 6(c) ; the d = 6.35 mm and Re = 13,000 case is shown to best illustrate the trends. The profiles show that decreasing H/d leads to an increase in the magnitude of the peak velocity. At small r/d the position of the peak is also shifted further away from the target plate for the smaller H/d. The effects of changes in H/d become negligible beyond r/d z 3. The radial velocity is shown in Fig. 7(a) and (b) as a function of radial position at several distances (z/d) from the target plate with a Reynolds number of 23,000, H/d = 4 and d = 3.18 mm. Very near the target plate (z/d < 0.1) the radial velocity exhibits a maximum value at r/d = 1 as seen in Fig. 7(a). The magnitude of the maximum in the profile is 0.89 Vj at z/d = 0.02, decreasing to 0.63 Vj further from the plate at z/d = 0.1, With further radial travel, these differ-
1030
J. A. FITZGERALD and S. V. GARIMELLA
ences in velocity with z/d show a reversed trend, with
a complete crossover occurring at r/d = 3. This crossover corresponds to a change in shape of the radial velocity profiles, u(r), with the peak in the profile moving away from the target plate (this is also brought out in Fig. 8(b) to follow). All the velocities then decelerate (in a narrow band) to zero at r/d = 16). Further away from the target plate (z/d > 0.2), the
(a)
0
r/d
0 -1
0 r/d
a *
Fig. 4. Mapping of the pre-impingement jet for d = 6.35 mm, velocity profiles through the jet showing jet spreading and decay of the potential core ; the dashed lines indicate the extent of the jet, and the dotted lines the potential core ; and (b) normalized axial turbulence intensity. (The target plate is located at z/d = 0, the nozzle plate at z/d = 4).
H/d = 4 and Re = 8500; (a) normalized
50z
1.25 1.00 ?? Re=8500 ARe=13000 VRe=23ooO
0.75 0
0.5
1.0
1.5
2.0
2.5
3.0
. 3.5 4.0
z/d Fig. 5. Normalized centerline velocity measurements for d = 6.35 mm and H/d = 4, at Re = 8500, 13,000 and 23,000. (The nozzle exit is at z/d = 4, and the target plate at z/d = 0.)
magnitude of the maximum velocity decreases and its location shifts toward the jet centerline as seen in Fig. 7(b). Negative velocities can be seen for r/d > 0.75 reflecting the recirculation pattern in the fluid. At large r/d (a 16) the radial velocity becomes negligible at all vertical locations in the confined flow field. It is seen from Fig. 7(b) that the effect of the impingement surface on the flow is not significant for z/d 2 1.25, since at this location the radial component of velocity is very small. The development of the wall jet can be seen more clearly in Fig. 8(a). As the radius increases from 0 to 1 d, the magnitude of velocity increases rapidly. The position of the maximum in radial velocity occurs at the measurement location nearest the target plate (z/d c 0.02) and r/d = 1. Beyond r/dof 1, the velocity decreases again as seen in Fig. 8(b), due to the increase in cross-sectional area as the jet spreads radially. A slight shift in the location of peak velocity away from the target plate is also noticed as r/d increases. These findings are consistent with the free-jet results of Stevens and Webb [l], except that in the latter, the shift of the peak velocity away from the wall is quite pronounced. The influence of nozzle-to-target plate spacing on the location and magnitude of the peak radial velocity is illustrated in Fig. 9(a). The figure shows normalized radial velocity profiles very near the target plate (z/d = 0.04) at Re = 23,000 and d = 6.35 mm for three spacings. The magnitude of the peak velocity increases as H/d is reduced, from 0.60 Vj at H/d = 4 to 1.17 V,at H/d = 2. The location of the peak velocity does not change significantly (remaining at 0.75 < r/d < 1 for all spacings). Increasing the nozzle diameter reduces the magnitude of the peak velocity while moving its radial location nearer to the jet axis. The normalized radial velocity is plotted for both nozzle diameters very close to the target plate (z/d = 0.04) for Re = 23,000 in Fig. 9(b). Increasing the nozzle diameter from 3.18 to 6.35 mm reduces the magnitude of the peak radial velocity from 0.85 V,to 0.60 yj while moving the location from r/d z 1 to r/d CT 0.75 in this case. All curves show a subsequent deceleration with increasing r/d. The turbulence intensities corresponding to the radial-velocity profiles discussed in Fig. 6(a) are presented in Fig. 10(a). Even at small r/d, the profiles show significant turbulence levels. The turbulence levels increase in magnitude up to r/d a 2 (which is the location identified for the onset of transition), and gradually decrease thereafter. These trends are better
Flow field of an impinging jet
1031
(W
2 r/d
Fig. 6. Profiles of normalized local radial velocity through the stagnation and wall jet regions: (a) d = 3.18 mm, H/d = 4, and Re = 23,000; (b) the same case showing wall jet development ; and (c) nozzle-to-target plate spacings of 2, 3 and 4, with d = 6.35 mm and Re = 13,000.
illustrated in Fig. 11. Increasing the nozzle-to-target plate spacing results in a decrease in turbulence levels near the target plate. A comparison of three nozzleto-target plate spacings for the 6.35 mm diameter nozzle and Re := 13,000 is shown in Fig. IO(b). The effect of nozzle- to-target plate spacing decreases as r/d increases, becoming negligible beyond r/d x 3.5. Figure 11 shows the radial distribution of the turbulence intensities measured at different distances from the target plate for a nozzle diameter of 3.18 mm with H/d = 4 and Re = 23,000. Measurements near the plate show a maximum level of turbulence of 17.8% at r/d = 2 (for z/d - O.l), signifying the transition from a laminar to a turbulent boundary layer. As z/d increases, the turbulence levels decrease and move radially outward as the turbulence diffuses through the boundary layer. At large z/d a second region of high turbulence can be seen to occur at r/d = 0.5 (corresponding to the edge of the nozzle itself). The turbulence in this region also diffuses through the flow radially, resulting in two local maxima in the intermediate range of z/d. The results from this study showed that for the range of turbulent flow rates (8500 < Re < 23,000) and nozzle-to-target plate spacings (2 <H/d < 4)
studied, the magnitude of the radial turbulence levels are not affected by a change in Reynolds number. Furthermore, the location where transition occurs was found not to change with Reynolds number. Stevens and Webb [l] reported higher peak levels of turbulence at higher Re in free-surface jets, but their data were for a narrower nozzle-to-target plate spacing of one and a fully developed jet. Higher peak levels of turbulence are observed for smaller nozzle-to-target plate spacings (21.8% at H/d z 2 compared to 18.6% at H/d z 4), as shown in Fig. 12(a). The location of transition to turbulence, identified by the r/d at which u,,/Vj drops sharply, moves radially outward as H/d is increased. Similarly, secondary peaks in heat transfer are more pronounced at smaller H/d and move radially outward for increasing H/d [14] ; however, the radial location of the secondary peaks in heat transfer occur further from the jet axis than the location of peak turbulence levels at the wall. The confined air jet study of Gillespie et al. [lo] also shows that secondary peaks in heat transfer occur downstream from the point of transition, in the region where the flow has become fully turbulent. Figure 12(b) shows turbulence measurements for two nozzle diameters at H/d = 4 and Re = 23,000. The larger nozzle exhibits only
1032
J. A. FITZGERALD
and S. V. GARIMELLA 1.25 1.00 ._0.75
(a)
w 0.50 0.25
-0.25
L2
0 4 6 8 10 12 14 16 18 20 22 r/d
12
5 r/d
1011
._ 0.50
0.25
-0.251, * I , 0 2 4 6 8 10 12 14 16 18 20 22 r/d Fig. 7. Normalized radial velocities at different distances from the impingement surface for d = 3.18 mm, H/d = 4, and Re = 23,000 : (a) 0.02 < z/d < 0.1 ; and (b) 0.02 < z/d c 3.5.
12
91011
r/d Fig. 9. Effect of (a) nozzle-to-target spacing (d = 6.35 mm) and (b) nozzle diameter (H/d = 4) on radial velocity near the target plate (z/d = 0.04) for Re = 23,000.
slightly higher levels of the radial component of turbulence over r/d < 4, as opposed to the much more significant difference in the axial component of turbulence levels seen in the pre-impingement jet measurements [17]. Correspondingly, the effect of nozzle diameter in Nusselt number distribution is significant in the stagnation region, but diminishes with distance from the jet axis [ 131.
0.4 i Y
CONCLUSIONS
0.2 ii
0.2
0.4 Nj
0.6
0.8
1.0
0.2
0.4 Nj
0.6
0.8
1.0
Fig. 8. Normalized radial velocities at different radial locations from the jet centerline for d = 3.18 mm, H/d = 4, andRe=23,0OO:(a)O~r/d~1;and(b)l~r/d,<11.
The flow field of a confined and submerged impinging liquid jet was investigated through velocity and turbulence measurements using laser-Doppler velocimetry. A toroidal recirculation zone observed in previous flow visualization studies was mapped. The location of the center of the toroid moved radially outward, both with an increase in Reynolds number and with an increase in nozzle-to-target plate spacing. The center of the toroid moved nearer to the target plate with an increase in Reynolds number. The maximum velocity in the wall jet region occurred very close to the impingement plate for r/d a 1, with the maximum turbulence levels occurring at r/d a 2. An increase in the nozzle-to-target plate spacing was shown to reduce the magnitudes of the radial velocities as well as the peak turbulence intensities in the flow field. Increasing the nozzle diameter resulted in a decrease in peak radial velocity, but an increase in peak turbulence levels. These differences became neg-
Flow field of an impinging jet
1033
r/d
%Dj +
H/u=2 H/d=4
---8_lUd=3 0.0 0.5 0.4 'c1 0.3 A 0.2 0.1 0.0 1 2 3
0.2
--
r/d
Fig. 10. Turbulence profiles (normalized with jet exit velocity) through the stagnation and wall jet regions for (a) d = :3.18mm, H/d = 4, and Re = 23,000; and (b) H/d = 2,3 and 4, d = 6.35 mm, and Re = 13,000.
r/d 0 2 4 6 8 10 12 14 16 18 20 22
r/d Fig. 11. Turbulence intensities at different distances (z/d) from the impingement surface for d = 3.18 mm, H/d = 4, and Re = 23,000.
(b)
ligible for r/d > 4. Comparisons were made with flowfield results from free jets and submerged but unconfined jets in the literature.
Acknowledgements--Partial funding for this work through a research grant from Cray Research Inc. of Chippewa Falls, Wisconsin, is gratefully acknowledged. This material is based upon work supported under a National Science Foundation Graduate Research Fellowship to JAF.
REFERENCES
0.05 : or 0 . 1
2 3
5 6
r/d Fig. 12. Effect of (a) nozzle-to-target spacing for d = 6.35 mm and (b) nozzle diameter for H/d = 4 on turbulence intensities near the target plate (z/d = 0.04) at Re = 23,000.
l-Turbulent
flow structure. Journal of Heat Transfer,
1992,114,874-879.
1. Stevens, J. and Webb, B. W., Measurements of the flow structure in th radial layer of impinging free-surface e liquid jets. International Journal of Heat and Mass Transfer, 1993,36, 3 751-3758. 2. Stevens, J., Pan, Y. and Webb, B. W., Effect of nozzle
Pan, Y., Stevens, J., and Webb, B. W., Effect of nozzle configuration on transport in the stagnation zone of axisymmetric, impinging free-surface liquid jets : Part 2-Local heat transfer. Journal of Heat Transfer, 1992,
114,880-886.
configuration ton transport in the stagnation zone of axisymmetric, impinging free-surface liquid jets : Part
Gardon, R. and Akfirat, J. C., The role of turbulence in determining the heat-transfer characteristics of
1034 impinging jets. International
Transfer, 1965,8, 1261-1272.
J. A. FITZGERALD
Journal of Heat and Mass
and S. V. GARIMELLA F. P. and Ramadhyani, S., Planar liquid jet impingement cooling of multiple disCrete heat sources. JournalofElectronic Packaging, 1991, 113,359-366. 12. Rice, R. A. and Garimella, S. V., Heat transfer from discrete heat sources using an axisymmetric, submerged and confined liquid jet, Proceedings of the Tenth International Heat Transfer Conference, Vol. 3, 1994, pp. 890 7Y. 13. Garimella, S. V. and Nenaydykh, B., Nozzle-geometry effects in liquid jet impingement heat transfer. International Journal of Heat and Mass 2915-2923. Transfer, 1996, 39, 14. Garimella, S. V. and Rice, R. A., Confined and submerged liquid jet impingement heat transfer. Journal of Heat Transfer, 1995, 117,871-877. 15. Morris, G. K., Prediction of heat transfer and flow fields 11. Schaefer, D., Incropera,
5. Hrycak, P., Lee, D. T., Gauntner, J. W. and Livingood, J. N. B., Experimental flow characteristics of a single turbulent jet impinging on a flat plate. NASA TN D5690, 1970, pp. l-32. 6. den Ouden, C. and Hoogendoorn, C. J., Local convective heat transfer coefficient for jets impinging on a plate : Experiments using a liquid technique. Proceedings of the Ftfth International Heat Transfer Conference, Vol. 5, 1974, pp. 293-297. I. Hoogendoorn, C. J., The effect of turbulence on heat transfer at a stagnation point. International Journal of Heat and Mass Transfer. 1977.20. 1333-1338. 8. Lytle, D. and Webb: B: W., Air jet impingement heat transfer at low nozzle-plate spacings. International Journal of Heat and Mass Transfer, 1994,37, 1687-1697.
9. Obot, N. T., Douglas, W. J. M. and Mujumdar, A. S., Effect of semi-confinement on impingement heat transfer. Proceedings of the Seventh International Heat Transfer Conference, 1982,3, 395400. 10. Gillespie, D. R. H., Guo, S. M., Wang, Z. and Ireland, P. T., A comparison of full surface local heat transfer coefficient and flow field studies beneath sharp-edged and radiused entry impinging jets. Paper No. 96-GT428, International Gas Turbine and Aeroengine Congress and Exhibition, 1996, Birmingham, U.K.
in submerged and axisymmetric impinging jets. M.S. thesis, Department of Mechanical Engineering, University of Wisconsin - Milwaukee, 1996. 16. Ashforth-Frost, S. and Jambunathan, K., Effect of nozzle geometry and semi-confinement on the potential core of a turbulent axisymmetric free jet. International
Communications 152-162. in Heat and Mass Transfer, 1996, 23, 17. Fitzgerald, J. A. and Garimella, S. V., Flow field effects on heat transfer in a confined impinging jet. Journal of Heat Transfer, 1997, 119,630-632.
Das könnte Ihnen auch gefallen
- Fluid Dynamics in Complex Fractured-Porous SystemsVon EverandFluid Dynamics in Complex Fractured-Porous SystemsBoris FaybishenkoNoch keine Bewertungen
- Wood Science TechnologyDokument13 SeitenWood Science TechnologymhNoch keine Bewertungen
- Wind Environment Over The Helideck of An Offshore PlatformDokument11 SeitenWind Environment Over The Helideck of An Offshore PlatformBagheri HessamNoch keine Bewertungen
- The Effect of Swirl On Array of Turbulent Impinging Jets: ICMIEE18-104Dokument5 SeitenThe Effect of Swirl On Array of Turbulent Impinging Jets: ICMIEE18-104bariNoch keine Bewertungen
- Deo Et Al 2007 - The Influence of Nozzle Exit Geometric Profile On A Turbulent Plane JetDokument15 SeitenDeo Et Al 2007 - The Influence of Nozzle Exit Geometric Profile On A Turbulent Plane JetDr Ravinesh C DeoNoch keine Bewertungen
- Ijps PDF Pdf2011 4jul Jaafar Et AlDokument8 SeitenIjps PDF Pdf2011 4jul Jaafar Et AlPatel HarshNoch keine Bewertungen
- Experimental investigation of backward-facing step flow using laser Doppler anemometryDokument24 SeitenExperimental investigation of backward-facing step flow using laser Doppler anemometryJennifer SmallNoch keine Bewertungen
- Armaly 1983Dokument24 SeitenArmaly 1983chaib benchaibNoch keine Bewertungen
- Effect of Inclination of Impinging Jets On Flow and Heat Transfer CharacteristicsDokument6 SeitenEffect of Inclination of Impinging Jets On Flow and Heat Transfer CharacteristicsInternational Journal of Science and Engineering InvestigationsNoch keine Bewertungen
- Wind Tunnel Velocity Profiles Generated by Differentially-Spaced Flat PlatesDokument10 SeitenWind Tunnel Velocity Profiles Generated by Differentially-Spaced Flat PlatesMario AlemanNoch keine Bewertungen
- Lee 2013 International Journal of Heat and Fluid FlowDokument13 SeitenLee 2013 International Journal of Heat and Fluid FlowalexandreburanNoch keine Bewertungen
- CFD Analysis and Experimental Investigations Towards Optimizing The Parameters of Ranque-Hilsch Vortex TubeDokument13 SeitenCFD Analysis and Experimental Investigations Towards Optimizing The Parameters of Ranque-Hilsch Vortex TubedennyfrancisNoch keine Bewertungen
- Aiaa 2011 573 500Dokument17 SeitenAiaa 2011 573 500Rajeev Raj'sNoch keine Bewertungen
- Experiments With Biconvex Aerof6ils in Low-Density, and Double-Wedge Supersonic FlowDokument46 SeitenExperiments With Biconvex Aerof6ils in Low-Density, and Double-Wedge Supersonic Flowaustin00012Noch keine Bewertungen
- An Investigation of The Volumetric. Efficiency of A Roots BlowerDokument9 SeitenAn Investigation of The Volumetric. Efficiency of A Roots BlowershreemugNoch keine Bewertungen
- Pressure Drop in Laminar and Turbulent Flows in Circular PipeDokument17 SeitenPressure Drop in Laminar and Turbulent Flows in Circular Pipegestapo85Noch keine Bewertungen
- Fadel AbbasDokument7 SeitenFadel Abbashosenasde1975Noch keine Bewertungen
- Blunted Cone-Flare in Hypersonic FlowDokument17 SeitenBlunted Cone-Flare in Hypersonic FlowMohsen SalehiNoch keine Bewertungen
- Characteristics of a Low-Speed Wind Tunnel EvaluatedDokument14 SeitenCharacteristics of a Low-Speed Wind Tunnel EvaluatedMario AlemanNoch keine Bewertungen
- Chew Packwood N TurnerDokument344 SeitenChew Packwood N TurnerBegan GurungNoch keine Bewertungen
- Hot Wire SynjetDokument8 SeitenHot Wire SynjetDaniel SilvaNoch keine Bewertungen
- Wind TunnelDokument11 SeitenWind TunnelKoushik RaoNoch keine Bewertungen
- 2016-Crossflows From Jet Array Impingement Cooling Hole Spacing, Target Plate Distance, Reynolds Number EffectsDokument12 Seiten2016-Crossflows From Jet Array Impingement Cooling Hole Spacing, Target Plate Distance, Reynolds Number EffectsSsheshan Pugazhendhi100% (1)
- Aiaa Airfoiljet 03Dokument11 SeitenAiaa Airfoiljet 03Namrata VermaNoch keine Bewertungen
- A Complementary Numerical and Physical Investigation of Vortex Induced Vibration 2001 Journal of Fluids and StructuresDokument9 SeitenA Complementary Numerical and Physical Investigation of Vortex Induced Vibration 2001 Journal of Fluids and StructuresValbort HernandezNoch keine Bewertungen
- General Disclaimer One or More of The Following Statements May Affect This DocumentDokument24 SeitenGeneral Disclaimer One or More of The Following Statements May Affect This DocumentAngel Villalonga MoralesNoch keine Bewertungen
- Research Article: Numerical Investigation On Pressure Fluctuations For Different Configurations of Vaned Diffuser PumpsDokument10 SeitenResearch Article: Numerical Investigation On Pressure Fluctuations For Different Configurations of Vaned Diffuser Pumpsbakri10101Noch keine Bewertungen
- Numerical Prediction of Laminar F L o W and Heat Transfer Characteristics in A Tube Fitted With Regularly Spaced Twisted-Tape ElementsDokument9 SeitenNumerical Prediction of Laminar F L o W and Heat Transfer Characteristics in A Tube Fitted With Regularly Spaced Twisted-Tape ElementschawarepNoch keine Bewertungen
- Thermal Science RevisedDokument16 SeitenThermal Science RevisedArivazhagan SundaraganesanNoch keine Bewertungen
- Three-Dimensional Optimization of Staggered Finned Circular and Elliptic Tubes in Forced Convection - MatosDokument11 SeitenThree-Dimensional Optimization of Staggered Finned Circular and Elliptic Tubes in Forced Convection - MatosMeshal Al-mutairiNoch keine Bewertungen
- (238866464) PaperDokument12 Seiten(238866464) PaperNatalia Cornejo MardonesNoch keine Bewertungen
- Measurement of Turbulence Characteristics in A Large Scale Fan Stirred Spherical VesselDokument20 SeitenMeasurement of Turbulence Characteristics in A Large Scale Fan Stirred Spherical VesselVeli Can CosarNoch keine Bewertungen
- Mathematical Modelling of Engineering Problems: Received: 11 July 2018 Accepted: 27 July 2018Dokument6 SeitenMathematical Modelling of Engineering Problems: Received: 11 July 2018 Accepted: 27 July 2018yanan.camarazaNoch keine Bewertungen
- PressureDrop IJFMRDokument18 SeitenPressureDrop IJFMRThinh Tran HungNoch keine Bewertungen
- Achenbach Smooth - Rough CylinderDokument15 SeitenAchenbach Smooth - Rough CylinderVivek KantiNoch keine Bewertungen
- Z AIAAJournal2007Dokument5 SeitenZ AIAAJournal2007engma3Noch keine Bewertungen
- Developing Heat Transfer in Rectangular Channels With Rib TurbulatorsDokument13 SeitenDeveloping Heat Transfer in Rectangular Channels With Rib Turbulatorshamid_zoka6069Noch keine Bewertungen
- Caracterización Túnel UNNEDokument14 SeitenCaracterización Túnel UNNELucy LopezNoch keine Bewertungen
- Important ThroughflowDokument14 SeitenImportant ThroughflowkoolwaveoceanicNoch keine Bewertungen
- Of Vortex Generators"": Final ReportDokument7 SeitenOf Vortex Generators"": Final Reportramazan akyolNoch keine Bewertungen
- Numerical Investigation of Heat Transfer Coefficient in Ribbed Rectangular Duct With Various Shaped Ribs and Different CoolantsDokument4 SeitenNumerical Investigation of Heat Transfer Coefficient in Ribbed Rectangular Duct With Various Shaped Ribs and Different CoolantsedNoch keine Bewertungen
- LES Investigation of Wake Development in A Transonic Fan Stage For Aeroacoustic AnalysisDokument12 SeitenLES Investigation of Wake Development in A Transonic Fan Stage For Aeroacoustic AnalysisMiguelMazzucchelliNoch keine Bewertungen
- Aerothermal Performance Measurements and AnalysisDokument8 SeitenAerothermal Performance Measurements and Analysisraul19rsNoch keine Bewertungen
- WCE2013 pp1628-1633Dokument6 SeitenWCE2013 pp1628-1633senadbalicNoch keine Bewertungen
- Study On Heat Transfer Area of A Plate-Fin Heat Exchanger With Wavy SurfacesDokument15 SeitenStudy On Heat Transfer Area of A Plate-Fin Heat Exchanger With Wavy SurfacesJignesh RohitNoch keine Bewertungen
- Boldyrev - Tunel de Vento HipersônicoDokument5 SeitenBoldyrev - Tunel de Vento HipersônicoalexandreburanNoch keine Bewertungen
- Fransson Jocker Bolcs Ott Igti490 98Dokument11 SeitenFransson Jocker Bolcs Ott Igti490 98HomeNoch keine Bewertungen
- ARCHIVE Proceedings of the Institution of Mechanical Engineers Conference Proceedings 1964-1970 (Vols 178-184) Various Titles Labelled Volumes a to S Volume 180 Issue 310 1965 [Doi 10.1243_PIME_CONFDokument13 SeitenARCHIVE Proceedings of the Institution of Mechanical Engineers Conference Proceedings 1964-1970 (Vols 178-184) Various Titles Labelled Volumes a to S Volume 180 Issue 310 1965 [Doi 10.1243_PIME_CONFSree288Noch keine Bewertungen
- Dong Ho Rhee 3Dokument12 SeitenDong Ho Rhee 3Yash MenonNoch keine Bewertungen
- 3 44482Dokument3 Seiten3 44482Ravi Kiran JanaNoch keine Bewertungen
- An Experimental Investigation of Free and Submerged Miniature Liquid Jet Array Impingement Heat TransferDokument13 SeitenAn Experimental Investigation of Free and Submerged Miniature Liquid Jet Array Impingement Heat TransferEKKACHAI PRABNAKORNNoch keine Bewertungen
- Ijmet 06 10 001Dokument9 SeitenIjmet 06 10 001IAEME PublicationNoch keine Bewertungen
- Y. F. Yao and N. D. Sandham - Direct Numerical Simulation of Turbulent Trailing-Edge Flow With Base Flow ControlDokument9 SeitenY. F. Yao and N. D. Sandham - Direct Numerical Simulation of Turbulent Trailing-Edge Flow With Base Flow ControlWhiteLighteNoch keine Bewertungen
- Aeroacoustic Optimization of Wind Turbine Airfoils by Combining Thermographic and Acoustic Measurement DataDokument4 SeitenAeroacoustic Optimization of Wind Turbine Airfoils by Combining Thermographic and Acoustic Measurement DatamoussaouiNoch keine Bewertungen
- Nilesh PPT TrainingDokument16 SeitenNilesh PPT TrainingsureshNoch keine Bewertungen
- Aerodynamics of A Multi-Element Airfoil Near Ground: LL LL LLDokument6 SeitenAerodynamics of A Multi-Element Airfoil Near Ground: LL LL LLVimal ChandNoch keine Bewertungen
- V25su2-3 18Dokument13 SeitenV25su2-3 18mhNoch keine Bewertungen
- Mean and Fluctuating Wind Loads On Rough and Smooth Parabolic DomesDokument17 SeitenMean and Fluctuating Wind Loads On Rough and Smooth Parabolic DomesMarco CamposNoch keine Bewertungen
- Experimental and Numerical Analyses of Different Extended SurfacesDokument8 SeitenExperimental and Numerical Analyses of Different Extended SurfacesAminul HoqueNoch keine Bewertungen
- Technical Note Turbulent Heat Transfer From A Convex Hemispherical Surface To A Round Impinging JetDokument10 SeitenTechnical Note Turbulent Heat Transfer From A Convex Hemispherical Surface To A Round Impinging JetEKKACHAI PRABNAKORNNoch keine Bewertungen
- Prandtl-Number Effect and Generalized Correlations For Confined and Submerged Jet ImpingementDokument10 SeitenPrandtl-Number Effect and Generalized Correlations For Confined and Submerged Jet ImpingementEKKACHAI PRABNAKORNNoch keine Bewertungen
- Welding CoatingDokument69 SeitenWelding CoatingspaljeniNoch keine Bewertungen
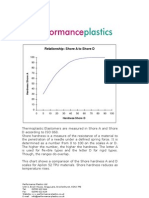
- ShoreA ShoreD Hardness RelationshipDokument1 SeiteShoreA ShoreD Hardness RelationshipengeniusNoch keine Bewertungen
- Numerical Investigation of Heat Transfer in Impinging Axial and Radial Jets With SuperimposedDokument7 SeitenNumerical Investigation of Heat Transfer in Impinging Axial and Radial Jets With SuperimposedEKKACHAI PRABNAKORNNoch keine Bewertungen
- Prediction of The Flow Structure in A Turbulent Rectangular Free JetDokument12 SeitenPrediction of The Flow Structure in A Turbulent Rectangular Free JetEKKACHAI PRABNAKORNNoch keine Bewertungen
- Simultaneous Visualization of Flow Field and Evaluation of Local Heat Transfer by Transitional Impinging JetsDokument11 SeitenSimultaneous Visualization of Flow Field and Evaluation of Local Heat Transfer by Transitional Impinging JetsEKKACHAI PRABNAKORNNoch keine Bewertungen
- Technical Note Turbulent Heat Transfer From A Convex Hemispherical Surface To A Round Impinging JetDokument10 SeitenTechnical Note Turbulent Heat Transfer From A Convex Hemispherical Surface To A Round Impinging JetEKKACHAI PRABNAKORNNoch keine Bewertungen
- Simultaneous Visualization of Flow Field and Evaluation of Local Heat Transfer by Transitional Impinging JetsDokument11 SeitenSimultaneous Visualization of Flow Field and Evaluation of Local Heat Transfer by Transitional Impinging JetsEKKACHAI PRABNAKORNNoch keine Bewertungen
- Investigation of Mixed Convection in A Large Rectangular EnclosureDokument8 SeitenInvestigation of Mixed Convection in A Large Rectangular EnclosureEKKACHAI PRABNAKORNNoch keine Bewertungen
- Simultaneous Heat and Mass Transfer Characteristics For Wavy Fin-And-tube Heat Exchangers Under Dehumidifying ConditionsDokument12 SeitenSimultaneous Heat and Mass Transfer Characteristics For Wavy Fin-And-tube Heat Exchangers Under Dehumidifying ConditionsEKKACHAI PRABNAKORNNoch keine Bewertungen
- An Impingement Cooling On A Flat Surface by Using Circular Jet With Longitudinal Swirling StripsDokument11 SeitenAn Impingement Cooling On A Flat Surface by Using Circular Jet With Longitudinal Swirling StripsEKKACHAI PRABNAKORNNoch keine Bewertungen
- Simultaneous Heat and Mass Transfer Characteristics For Wavy Fin-And-tube Heat Exchangers Under Dehumidifying ConditionsDokument12 SeitenSimultaneous Heat and Mass Transfer Characteristics For Wavy Fin-And-tube Heat Exchangers Under Dehumidifying ConditionsEKKACHAI PRABNAKORNNoch keine Bewertungen
- Study of Heat Transfer For A Pair of Rectangular Jets Impinging On An Inclined SurfaceDokument15 SeitenStudy of Heat Transfer For A Pair of Rectangular Jets Impinging On An Inclined SurfaceEKKACHAI PRABNAKORNNoch keine Bewertungen
- Forced Convective Heat Transfer With Impinging Rectangular JetsDokument11 SeitenForced Convective Heat Transfer With Impinging Rectangular JetsEKKACHAI PRABNAKORNNoch keine Bewertungen
- Comparison of Turbulent Jets Issuing From Rectangular Nozzles With and Without SidewallsDokument11 SeitenComparison of Turbulent Jets Issuing From Rectangular Nozzles With and Without SidewallsEKKACHAI PRABNAKORNNoch keine Bewertungen
- Influence of Shear Layer Dynamics OnDokument9 SeitenInfluence of Shear Layer Dynamics OnEKKACHAI PRABNAKORNNoch keine Bewertungen
- An Experimental Investigation of Free and Submerged Miniature Liquid Jet Array Impingement Heat TransferDokument13 SeitenAn Experimental Investigation of Free and Submerged Miniature Liquid Jet Array Impingement Heat TransferEKKACHAI PRABNAKORNNoch keine Bewertungen
- Effects of Acoustic Excitation Positions On Heat Transfer and Flow in Axisymmetric Impinging Jet Main Jet Excitation and Shear Layer ExcitationDokument11 SeitenEffects of Acoustic Excitation Positions On Heat Transfer and Flow in Axisymmetric Impinging Jet Main Jet Excitation and Shear Layer ExcitationEKKACHAI PRABNAKORNNoch keine Bewertungen
- Impingement Cooling Confined Circular Air JetDokument10 SeitenImpingement Cooling Confined Circular Air JetEKKACHAI PRABNAKORNNoch keine Bewertungen
- Epri 501a-DDokument154 SeitenEpri 501a-DEKKACHAI PRABNAKORN100% (2)
- Local Heat Transfer Due To Several Configurations of Circular Air JetsDokument11 SeitenLocal Heat Transfer Due To Several Configurations of Circular Air JetsEKKACHAI PRABNAKORNNoch keine Bewertungen
- Local Convective Heat Transfer From A Constant Heat Flux Flat Plate Cooled by Synthetic Air JetsDokument11 SeitenLocal Convective Heat Transfer From A Constant Heat Flux Flat Plate Cooled by Synthetic Air JetsEKKACHAI PRABNAKORNNoch keine Bewertungen
- Heat Transfer Enhancement of Impinging JetsDokument12 SeitenHeat Transfer Enhancement of Impinging JetsEKKACHAI PRABNAKORNNoch keine Bewertungen
- Heat and Mass Transfer in Impingement DryingDokument31 SeitenHeat and Mass Transfer in Impingement DryingEKKACHAI PRABNAKORNNoch keine Bewertungen
- Heat Transfer and Flow Structures in Axisymmetric Impinging Jet Controlled by Vortex PairingDokument8 SeitenHeat Transfer and Flow Structures in Axisymmetric Impinging Jet Controlled by Vortex PairingEKKACHAI PRABNAKORNNoch keine Bewertungen
- Epri 501a-DDokument154 SeitenEpri 501a-DEKKACHAI PRABNAKORN100% (2)
- Electronic Cooling Using Synthetic Jet ImpingementDokument11 SeitenElectronic Cooling Using Synthetic Jet ImpingementEKKACHAI PRABNAKORNNoch keine Bewertungen
- Flow and Mass Transfer Measurements For A Flat Plate of FiniteDokument10 SeitenFlow and Mass Transfer Measurements For A Flat Plate of FiniteEKKACHAI PRABNAKORNNoch keine Bewertungen
- Weld DiscontinuityDokument61 SeitenWeld DiscontinuityEKKACHAI PRABNAKORN0% (1)
- Interaction & Bank EffectDokument6 SeitenInteraction & Bank EffectAkash KandwalNoch keine Bewertungen
- Scania 12L - EMS - Operator - Manual - enDokument60 SeitenScania 12L - EMS - Operator - Manual - enАнатолий ЩербаковNoch keine Bewertungen
- Failure Analysis of Syngas Bypass Line Rupture inDokument11 SeitenFailure Analysis of Syngas Bypass Line Rupture inshahgardezNoch keine Bewertungen
- January2016page1to36 Layout 1Dokument36 SeitenJanuary2016page1to36 Layout 1c737Noch keine Bewertungen
- Steam System DesignDokument74 SeitenSteam System DesignIshan RanganathNoch keine Bewertungen
- Sru Flow DiagramDokument1 SeiteSru Flow Diagrampppppp5Noch keine Bewertungen
- Physics ExamDokument30 SeitenPhysics Examjomar bolasocNoch keine Bewertungen
- Lab Sheet - Infiltration TestDokument8 SeitenLab Sheet - Infiltration TestDINAMARIANASAMUJI0% (1)
- 2014 Solder Joint ReliabilityDokument18 Seiten2014 Solder Joint ReliabilitychoprahariNoch keine Bewertungen
- 2 Interference in Spur GearsDokument2 Seiten2 Interference in Spur Gearschris100% (1)
- Ornl 2465Dokument101 SeitenOrnl 2465jesusNoch keine Bewertungen
- Please Note That This Form Details Exploration and Production Api Titles Available For OrderDokument8 SeitenPlease Note That This Form Details Exploration and Production Api Titles Available For Orderhaotran68Noch keine Bewertungen
- Instructions pour pied SeniorDokument52 SeitenInstructions pour pied SeniorPriyanka PatilNoch keine Bewertungen
- Simucube 2 Quick Release GuideDokument7 SeitenSimucube 2 Quick Release Guideemyrs12Noch keine Bewertungen
- ESAB Welding HandbookDokument31 SeitenESAB Welding Handbookhooky1100% (4)
- XHLE Long Coupled Centrifugal Pump EnglishDokument8 SeitenXHLE Long Coupled Centrifugal Pump Englishgagi1994brahimNoch keine Bewertungen
- Quotation 615-4078 BabulalDokument14 SeitenQuotation 615-4078 Babulaldevrajan631Noch keine Bewertungen
- Applied Fluid Mechanics: Viscosity of FluidsDokument22 SeitenApplied Fluid Mechanics: Viscosity of FluidsMaggie HepditchNoch keine Bewertungen
- Rockaway Beach Branch Community Impact StudyDokument98 SeitenRockaway Beach Branch Community Impact StudyHanaRAlbertsNoch keine Bewertungen
- Nature of Acidity and Lime Requirement in Acid Soils of ManipurDokument8 SeitenNature of Acidity and Lime Requirement in Acid Soils of ManipurIJASRETNoch keine Bewertungen
- QADokument170 SeitenQASudama KhatriNoch keine Bewertungen
- INTERCOMP Pt300 Users Manual Rev GDokument44 SeitenINTERCOMP Pt300 Users Manual Rev GCTN2010Noch keine Bewertungen
- Reinforced ConcreteDokument13 SeitenReinforced ConcreteRenukadevi Rpt17% (18)
- Dow Corning (R) 200 Fluid, 50 Cst.Dokument11 SeitenDow Corning (R) 200 Fluid, 50 Cst.Sergio Gonzalez GuzmanNoch keine Bewertungen
- New Schedule For Sunset Limited Benefits Passengers and Improves Financial PerformanceDokument3 SeitenNew Schedule For Sunset Limited Benefits Passengers and Improves Financial Performanceapi-26433240Noch keine Bewertungen
- Master Opp GaveDokument84 SeitenMaster Opp GaveRizki Al AyyubiNoch keine Bewertungen
- GENG 8000 Final Project Memo - W19 FinalDokument2 SeitenGENG 8000 Final Project Memo - W19 Finalஇலக்கியா ராஜாNoch keine Bewertungen
- Establishing OPC UA Connectivity With Rockwell Automation® Integrated ArchitectureDokument3 SeitenEstablishing OPC UA Connectivity With Rockwell Automation® Integrated ArchitecturehuiyitNoch keine Bewertungen
- ETN2A ElectromechanicsDokument64 SeitenETN2A ElectromechanicsEinstein's VanderbijlparkNoch keine Bewertungen
- ESD Protection in CMOS: Characterization and Failure AnalysisDokument113 SeitenESD Protection in CMOS: Characterization and Failure AnalysisElisavNirolfNoch keine Bewertungen