Time Series Econometrics

Assignment 2

by

Roman Schmid 05-603-295

A . Unit-root Simulations
The task is to simulate sequences of the pure random walk process (1) of size and to discard the first 50 observed values. Then, the following three scenarios have to be estimated by OLS for each sequence: (2) (3) (4)

Then the -ratio and its distribution has to be computed for every model in order to find the 5 th percentiles of the distribution. The -ratio ratio is calculated by the formula (5)

for

In lecture 6, it is shown that

(6)

With

being a Wiener process and

. It is stated that

is a random

variable which is non-normal and skewed. Furthermore it is shown that

1

(7)

where the denominator is a random variable. So the -ratio becomes

(8)

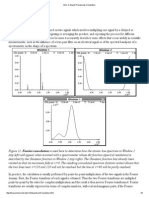
and the numerator is a product of two random variables while the denominator is a consistent estimator and converging to . The estimation result of scenario 1, 2 and 3 show a different distribution of the -ratio of the coefficient . Like mentioned in the lecture notes, the distribution of changes by adding of an intercept and/or by adding a deterministic time trend. Figure 1 below shows the distribution of the -ratio from each of the three model estimated with a kernel1 bandwith of 1. It can be seen that by adding an intercept to the pure random walk like in scenario 2 the distribution changes, e.g. becomes skewed to the left. If an intercept and a time trend is added like in scenario 3, then the distribution becomes even more left-skewed.

Figure 1:Distribution of the -ratio in each model

0.35 no intercept, no trend intercept, no trend intercept, trend

0.3

0.25

0.2

0.15

0.1

0.05

0 -10

-8

-6

-4

-2

Here I used a normal kernel smoother

For this simulation2, the 5th percentile of the distribution of the -ratio for scenario 1 is . As scenario 2 is more left-skewed, its 5th percentile of the distribution is . The distribution in scenario 3 has a 5th percentile of .

B. Decompositions
Part I:
a) The task in this part is to take US real GDP series and to log it so that . Then an AR(2) model with a constant has to be fitted to by OLS and the permanent and transitory components using the Beveridge-Nelson (BN) decomposition have to be found. The estimation for the AR(2) process gives the coefficients , and . Without going too far into detail, the BN-decomposition states that has two parts: a permanent part and a transitory part , so (9) BN assume that the permanent part is drift. Therefore , e.g. a random walk with

(10) The conditional mean is calculated by (11)

As of Lecture 6, (12) and (13)

As in an AR(p) model, no lags on are assumed, therefore integration back to the permanent part becomes

. By turning the

Percentiles change if the simulation of the pure random walk in (1) is repeated

(14)

The transitory part can simply be found by calculating (15) respectively, (16) Figure 2 below shows the permanent part (10) and the transitory part (15) using the BN decomposition. One can see that the transitory part is noisier than as of . Figure 3 below shows the permanent part (14) and the transitory part (16).

Figure 2: Permanent part and transitory part of

0.15 0.1
dy

using the BN decomposition

dy t dy P t,BN

0.05 0 -0.05

50

100

150 t

200

250

300

0.04 0.02
dy

dy T t,BN

0 -0.02 -0.04

50

100

150 t

200

250

300

Figure 3: Permanent part and transitory part of

10 y 9 yP t,BN

using the BN decomposition

y
8 7 0

50

100

150 t

200

250

300

0.02 0 -0.02 -0.04 -0.06 yT t,BN

50

100

150 t

200

250

300

b) Now the Hodrick-Prescott (HP) filter is applied to find the permanent and transitory component of both and . Without losing too much time on the theory, the HP filter applied for some time series chooses the permanent part for all such that

(17)

Where . The parameter is a smoothing parameter and generally set to 1600 for quarterly data like in . Figure 4 below shows the permanent part and the the transitory part of . One can see that the permanent part is smoother than the permanent part using the BN decomposition because of Figure 5 shows the permanent and transitory part for Like before, the permanent part using the HP filter is like a smooth line through

Figure 4: Permanent part and transitory part of

0.04 0.02
dy

using the HP filter

dy t dy P t,HP

0 -0.02 -0.04

50

100

150 t

200

250

300

0.04 0.02
dy

dy T t,HP

0 -0.02 -0.04

50

100

150 t

200

250

300

Figure 5: Permanent part and transitory part of

10 y 9
y

using the HP filter

yP t,HP

50

100

150 t

200

250

300

0.1 0.05 0 -0.05 -0.1

y

yT t,HP

50

100

150 t

200

250

300

c) By comparing the transitory parts of with respect to the BN decomposition and the HP filter, one can obtain that in the BN- case the time series of the transitory part seems to evolve below zero over time. In both the BN- and the HP- case, there seems to be some pattern in the time series of the transitory part, e.g. some predictive structure. The reason for this argumentation is that if we consider the transitory parts of , one cannot really see whether the parts have some white noise structure or not. But the transitory parts of are in fact the cumulative sum of the transitory parts of and so, if was a random walk, then would not have that kind of a stationary structure as in Figure 6.

Figure 6: Transitory part of

0.1 0.05 0 -0.05 -0.1
y

and

with both the BN and HP decomposition

yT t,BN yT t,HP

50

100

150 t

200

250

300

0.04 0.02
dy

dy T t,BN dy T t,HP

0 -0.02 -0.04

50

100

150 t

200

250

300

Figure 7 below shows the permanent parts of as well as in both the BN- and the HP- case. One can obtain that in both and the permanent part found by the HP filter is smoother than the permanent part found by the BN decomposition. This is due to the fact that the HP filter is rather a smoother than a filter because of the smoothing parameter
Figure 7: Permanent part of
10

and

with both the BN and HP decomposition

9
y

yP t,BN yP t,HP

50

100

150 t

200

250

300

0.15 0.1
dy

dy P t,BN dy P t,HP

0.05 0 -0.05

50

100

150 t

200

250

300

Part II:
a) The permanent part of a pure random walk (RW) process of the form (18) is the RW itself, e.g. there is no transitory part in a time series which is a pure RW.
7

Proof: Let the BN decomposition be done by approximating the RW by an ARMA(p,q) model of the integrated variable : (19) As in fore , the lag operator and there are no lags in , so . There-

(20) Furthermore, there is no constant . Therefore the process is which means that there is no unconditional mean

(21)

b) The transitory component of a large simulation of a pure RW found by the HP filter looks like in Figure 8. So far it looks like is white noise. But according to the lecture notes, simulations show that the transitory component in a pure unit RW like here is a persistent AR(2) process. By estimating an AR(2) with respect to the time series of the transitory component (constant included) gives the coefficients , and (estimates vary by repeating the simulation of the RW). Therefore the transitory part is stationary and it seems that its long run average is (consequently, the long run average varies too by repeating the simulation of the RW). Figure 9 below shows the transitory part of a RW simulation of size 100 and a corresponding AR(2) fit to the time series. It looks like that the AR(2) model fits the transitory part of a RW found by the HP filter quite well.
of a pure RW of size 10000

Figure 8: Transitory component

5 4 3 2 1 0 -1 -2 -3 -4 -5
x

xT t,HP xT t,BN 0 1000 2000 3000 4000 5000 t 6000 7000 8000 9000 10000

Figure 9: Transitory component

3

of a pure RW of size 100 and AR(2) fit

-1 xT t,HP AR(2) fit xT t,BN -3 0 10 20 30 40 50 t 60 70 80 90 100

-2

C. VARs
Consider the following VAR(2) macroeconomic model, where is the output growth and is inflation, taking the form is the money growth,

(22)

(23) and (24)

where (25)

a) The system in its companion form looks as follows: (26)

9

with

(27)

where

(28)

The stability/stationarity of the system can be found by looking at the Eigenvalues of . The system is said to be stable/stationary if , . The vector . As can be seen, the system is stable/stationary.

b) The unconditional mean vector

of

is calculated as (29)

(30)

which gives from

. The variance of

is computed

10

(31)

whereas

(32)

Reshaping

yields

(33)

MATLAB gives the solution

(34)

so that the variance of

is (35)

and the covariance is

11

(36)

c) The cholesky decomposition of

into

gives for the lower triangular : (37)

The first 12 impulse responses of , and are computed as follows: first calculate the first twelve coefficients of the VMA( ) representation:

(38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50)

Then, calculate the impulse response matrices

by applying the lower triangular .

(51)

(52)

12

(53)

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

(62)

(63)

Figure 10 12 below report the responses of each variable to different shocks. For example a shock in inflation will have a positive impact on output growth and also a positive impact on money growth in future lags. Figure 10 shows nicely that a shock in inflation will have a relatively high impact on money growth in future lags. Note that Figure 10 12 show impulse responses to one-standard deviation shocks in If the variables are logged then the impulse responses can be interpreted as elasticities.
13

Figure 11: Responses of inflation

to shocks in

Figure 10: Responses of money growth

to shocks in

0.5 0.45 0.4 0.35 0.3 u1 u2 u3

0.9 0.8 0.7 0.6 0.5 u1 u2 u3

0.25
0.4

0.2
0.3

0.15 0.1 0.05 0

0.2 0.1 0

5 t

10

5 t

10

Figure 12: Responses of output growth

0.35

to shocks in

0.3

u1 u2 u3

0.25

0.2

0.15

0.1

0.05

5 t

10

14