4.

3
Using Derivatives
for Curve Sketching
Greg Kelly, Hanford High School, Richland, Washington Photo by Vickie Kelly, 1995
Old Faithful Geyser, Yellowstone National Park
4.3
Using Derivatives
for Curve Sketching
Greg Kelly, Hanford High School, Richland, Washington Photo by Vickie Kelly, 2007
Yellowstone Falls, Yellowstone National Park
4.3
Using Derivatives
for Curve Sketching
Greg Kelly, Hanford High School, Richland, Washington Photo by Vickie Kelly, 2007
Mammoth Hot Springs, Yellowstone National Park
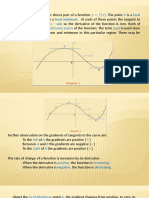
In the past, one of the important uses of derivatives was as
an aid in curve sketching. Even though we usually use a
calculator or computer to draw complicated graphs, it is still
important to understand the relationships between
derivatives and graphs.

First derivative:
y
'
is positive
Curve is rising.
y
'
is negative
Curve is falling.
y
'
is zero
Possible local maximum or
minimum.
Second derivative:
y
''
is positive
Curve is concave up.
y
''
is negative
Curve is concave down.
y
''
is zero
Possible inflection point
(where concavity changes).

Example:
Graph
( )( )
2
3 2
3 4 1 2 y x x x x = + = +
There are roots at and . 1 x = 2 x =
2
3 6 y x x
'
=
0 y
'
= Set
2
0 3 6 x x =
2
0 2 x x =
( )
0 2 x x =
0, 2 x =
First derivative test:
y
'
0 2
0 0

+ +
( )
2
1 3 1 6 1 3 y
'
= =
negative
( ) ( ) ( )
2
1 3 1 6 1 9 y
'
= =
positive
( )
2
3 3 3 6 3 9 y
'
= =
positive

Possible extreme at .
0, 2 x =
We can use a chart to organize our thoughts.
Example:
Graph
( )( )
2
3 2
3 4 1 2 y x x x x = + = +
There are roots at and . 1 x = 2 x =
2
3 6 y x x
'
=
0 y
'
= Set
2
0 3 6 x x =
2
0 2 x x =
( )
0 2 x x =
0, 2 x =
First derivative test:
y
'
0 2
0 0

+ +

maximum at 0 x =
minimum at 2 x =

Possible extreme at .
0, 2 x =
Example:
Graph
( )( )
2
3 2
3 4 1 2 y x x x x = + = +
2
3 6 y x x
'
= First derivative test:
y
'
0 2
0 0

+ +

NOTE: On the AP Exam, it is not sufficient to simply draw

the chart and write the answer. You must give a written
explanation!
There is a local maximum at (0,4) because for all x in
and for all x in (0,2) .
0 y
'
>
( , 0)
0 y
'
<
There is a local minimum at (2,0) because for all x in
(0,2) and for all x in .
0 y
'
<
(2, )
0 y
'
>
Because the second derivative at
x = 0 is negative, the graph is
concave down and therefore (0,4) is a
local maximum.
Example:
Graph
( )( )
2
3 2
3 4 1 2 y x x x x = + = +
There are roots at and . 1 x = 2 x =
2
3 6 y x x
'
= Possible extreme at .
0, 2 x =
Or you could use the second derivative test:

6 6 y x
''
=
( )
0 6 0 6 6 y
''
= =
( )
2 6 2 6 6 y
''
= = Because the second derivative at
x = 2 is positive, the graph is
concave up and therefore (2,0) is a
local minimum.

inflection point at 1 x =
There is an inflection point at x = 1 because the second
derivative changes from negative to positive.
Example:
Graph
( )( )
2
3 2
3 4 1 2 y x x x x = + = +

6 6 y x
''
=
We then look for inflection points by setting the second
derivative equal to zero.
0 6 6 x =
6 6x =
1 x =
Possible inflection point at .
1 x =
y
''
1
0

+
( )
0 6 0 6 6 y
''
= =
negative
( )
2 6 2 6 6 y
''
= =
positive
4 3 2 1 0 -1 -2
5
4
3
2
1
0
-1
4 3 2 1 0 -1 -2
5
4
3
2
1
0
-1
Make a summary table:
x y
y
' y''
1 0 9 12 rising, concave down
0 4 0 6
local max
1 2 3 0
falling, inflection point
2
0 0 6
local min
3 4 9 12
rising, concave up
t