ANALISIS MATEMATICO II:

1. Derivadas parciales

2. Plano tangente y recta normal

3. Derivadas parciales sucesivas (o de orden superior)
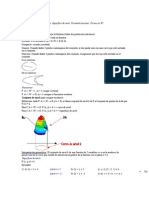
Sea z = f(x, y) una funcin de dos variables con dominio D. Si mantenemos la va-
riable y fija: y = b, siendo b una constante, y suponemos que solo la x vara, la fun-
cin f se convierte entonces en funcin de solo la variable x: g(x) = f(x, b). Si g tiene
derivada en a, entonces esta se llama derivada parcial de f respecto de x en(a, b),
que denotamos por f
x
(a, b). Luego por definicin se tiene:

f
x
(a, b) = g(a) =
0
g(a+h)-g(a)
lim
h
h
, por tanto

f
x
(a, b) =
0
f(a+h, b)-f(a, b)
lim
h
h


Anlogamente se define la derivada parcial de f respecta de y en (a, b), y que deno-
tamos por f
y
(a, b), que se obtiene fijando x = a, y obteniendo la derivada en b de la
funcin h(y) = f(a, y)


0
y
f(a, b+h)-f(a, b)
f (a, b) lim
h
h
=

Derivadas parciales
3
y=b
z=f(x, y)
y
x
z
z=f(x, b)
P(a, b, f(a, b))
Corte de z = f(x, y) con y = b
b
x = a
x
z
z=f(x, b)
Proyeccin del corte de z=f(x, y) con y = b
sobre el plano ZX
tg b = fx(a, b)

Si consideramos la superficie que tiene por ecuacin z = f(x, y), el plano y = b, corta
a la superficie en la curva z = f(x, b), que tiene por pendiente en el punto x = a, el
valor de su derivada en dicho punto, que es precisamente:

f
x
(a, b) =
0
f(a+h, b)-f(a, b)
lim
h
h

Interpretacin geomtrica de la derivada parcial
4
Anlogamente, si cortamos la superficie por el plano x = a, se obtiene la curva z
=f(a,y), que tiene por pendiente en el punto y = b, el valor de su derivada en dicho
punto:

0
y
f(a, b+h)-f(a, b)
f (a, b) lim
h
h
= .
Interpretacin geomtrica de la derivada parcial
x=a
y=b
z=f(a, y)
z=f(x,y)
z
x
y
P(a, b, f(a,b))
Corte de z=f(x, y) con x=a
z
y
a
f
y
(a, b)=tg a
y=b
Proyeccin del corte de z = f(x, y)
con x = a sobre el plano ZY
Suponiendo que el plano tangente a la superficie z = f(x, y) en el punto P(a, b, f(a,
b)) existe obtengamos su ecuacin. Dicho plano debe contener a las rectas tangen-
tes a la curvas contenidas en la superficie y que pasan por P(a, b, f(a, b)); en parti-
cular contendr a las rectas tangentes a las curvas que resultan de cortar a la su-
perficie por los planos x = a, y = b.
Al cortar por x = a, se obtiene la curva z = f(a, y) en el plano ZY, y cuya recta tan-
gente en el punto P(a ,b, f(a, b)) tiene por pendiente f
y
(a, b), luego un vector direc-
tor de esta recta ser de la forma (0, u, v) , siendo
y
v
=f (a, b)
u
, tomando u = 1, se
obtiene: v = f
y
(a, b)
es decir, un vector en la direccin de la recta tangente es (0, 1, f
y
(a, b)).
Plano tangente
x=a
y=b
z=f(a, y)
z=f(x,y)
z
x
y
P(a, b, f(a,b))
Corte de z=f(x, y) con x=a
a
Vector director = (1, fy(a, b))
Vector director = (0, 1, fy(a, b))
tg a = fy(a, b)
Plano tangente
y=b
z=f(x, y)
y
x
z
z=f(x, y)
P(a, b, f(a, b))
Corte de z = f(x, y) con y = b
b
tg b = fx(a, b)
Vector director = (1, 0, fx(a, b))
Vector director = (1, fx(a, b))
z = f(x, b)
Plano tangente
Anlogamente, al cortar por y = b, se obtiene la curva z = f(x, b) en el plano ZX, y
cuya recta tangente en el punto P(a ,b, f(a, b)) tiene por pendiente f
x
(a, b), luego un
vector director de esta recta ser de la forma (u, 0, v), siendo
x
v
=f (a, b)
u
, tomando
u = 1, se obtiene v = f
x
(a, b), es decir, un vector en la direccin de la recta tangente
es (1, 0, f
x
(a, b)).
Plano tangente y recta normal
En consecuencia dos vectores directores del plano tangente en el punto :
P(a ,b, f(a, b)) son p = (0, 1, f
y
(a, b)) y q = (1, 0, f
x
(a, b), luego un vector perpendicu-
lar al plano se obtendr multiplicndolos vectorialmente
pq = 0 1
1 0
y
x
f (a, b)
f (a, b)
i j k
=
x y
f (a, b)i+f (a, b)j-k
Por lo tanto el plano tangente queda definido por el punto P(a ,b, f(a, b)) y tiene
por vector caracterstico
x y
(f (a, b),f (a, b),-1) , por lo que su ecuacin ser:

f
x
(a, b)(x - a) + f
y
(a, b)(y - b) (z f(a, b)) = 0.

La recta perpendicular al plano tangente en el punto P(a ,b, f(a, b)) se llama recta
normal a la superficie en dicho punto, por lo que su ecuacin, en forma paramtri-
ca, ser

x
y
x=a+tf (a, b)
y=b+tf (a, b)
z=f(a, b)-t

)

Ejemplo

Obtener la ecuacin del plano tangente a la superficie z = 3x
2
-y
2
, en el punto
P(1, 1, 2),as como la ecuacin de la recta normal en dicho punto.

En este caso:

f
x
(x, y) = 6x, f
y
(x, y) = -2y, (a, b) = (1, 1) f
x
(1, 1) = 6, f
y
(1, 1) = -2, f(1, 1) = 2.

Luego la ecuacin del plano tangente es:

6(x-1)-2(y-1)-(z-2) = 0 6x-2y z = 2.

La recta normal tiene por ecuacin:


x=1+6t
y=1-2t
z=2-t

)

Plano tangente y recta normal
Plano tangente
en P(a, b, f(a, b))
x = a
y = b
Recta normal
P(a, b, f(a, b))
Plano tangente y recta normal
Plano tangente y recta normal
Si (a, b), es un punto variable lo representaremos por (x, y) y obtendremos el con-
cepto de funciones derivadas parciales:
La derivada parcial de f con respecto de x, la denotamos por f
x
, y se define as


0
x
f(x+h, y)-f(x, y)
f (x, y) lim
h
h
=
para todos los puntos (x, y) donde este lmite exista.

La derivada parcial de f con respecto de y, la denotamos por f
y
, y se define as


0
y
f(x, y+h)-f(x, y)
f (x, y) lim
h
h
=
para todos los puntos (x, y) donde este lmite exista.

Si z = f(x, y), otras notaciones usuales para las derivadas parciales son

f
x
(x, y) = z
x
=
f z
(x, y)=
x x
c c
c c

f
y
(x, y) = z
y
=
f z
(x, y)=
y y
c c
c c

Funcin derivada parcial
Como en el clculo de derivadas parciales una de las variables se mantiene cons-
tante, se podrn aplicar las reglas de derivacin para funciones de una variable,
siempre que est clara la existencia de esta derivada.

Ejemplo

Siendo f(x, y) = (x
2
+ y)e
xy
, calcular sus derivadas parciales y evaluarlas en el punto
(1,1):
f
x
(x, y) = 2xe
xy
+ (x
2
+ y)ye
xy
f
x
(1, 1) = 2e + 2e = 4e

f
y
(x, y) = e
xy
+ (x
2
+ y)xe
xy
f
y
(1, 1) = e + 2e = 3e

Se han aplicado directamente las reglas de derivacin de funciones de una varia-
ble, ya que al fijar una variable la funcin se convierte en una funcin derivable
por ser el resultado de operar funciones derivables. Esta funcin admite derivadas
parciales en todo punto de R
2
.

Derivadas parciales
Ejemplo

Estudiar la existencia de derivadas parciales, para cualquier punto, de la funcin
f(x, y) = |x+y|=
x+y si x+y>0
-x-y si x+y 0

calculndolas en su caso

Si x+y = 0, existen ambas derivadas parciales, ya que al fijar una variable se obtie-
ne un polinomio que siempre es derivable, siendo

f
x
(x, y) = 1, f
y
(x, y) = 1, si x+y>0
f
x
(x, y) = -1, f
y
(x, y) = -1, si x+y s 0

Queda por estudiar cuando el punto P(a, b) si x+y = 0, es decir, b = -a P(a, -a)
0 0
x
f(a+h, -a)-f(a, -a) |h|
f (a, -a) lim lim
h h
h h
= = , que no existe, ya que vale 1 o -1
segn que h tienda acero por la derecha o por la izquierda.
0 0
y
f(a, -a+h)-f(a, -a) |h|
f (a, -a) lim lim
h h
h h
= = , que no existe, ya que vale 1 o -1
segn que h tienda acero por la derecha o por la izquierda.

Luego la funcin admite derivadas parciales en todos los puntos, salvo en la recta
x + y = 0.
Derivadas parciales
Ejercicio

Estudiar la existencia de derivadas parciales, para cualquier punto, de la fun-
cin:

2 2
xy
si (x, y) (0, 0)
( , ) x +y
0 si (x, y)=(0, 0)
f x y

=

Derivadas parciales
Al calcular las derivadas parciales de una funcin de dos variables se obtienen
tambin funciones de dos variables, a las que se les puede calcular sus derivadas
parciales, a las que llamamos derivadas parciales segundas. Este proceso puede
seguir obtenindose las derivadas sucesivas (o de orden superior). Las notaciones
mas usuales son:
Derivadas parciales segundas:

1) derivando dos veces respecto de x

2
xx 2
f f
( )= =f
x x x
c c c
c c c

2) derivando dos veces respecto d e y

2
yy 2
f f
( )= =f
y y y
c c c
c c c

3) derivando primero respecto de x y luego respecto de y
2
xy
f f
( )= =f
y x y x
c c c
c c c c

4) derivando primero respecto de y y luego respecto de x

2
yx
f f
( )= =f
x y x y
c c c
c c c c


En las dos notaciones utilizadas se deriva primero respecto a la variable ms cer-
cana a f.
Derivadas parciales sucesivas
Ejemplo

Calcular las derivadas parciales segundas de:

f(x, y) =
2 x
x
y e +cos(xy)+
y


-
2 x
x
1
f (x, y)=y e -ysen(xy)+
y

-
x
y 2
x
f (x, y)=2ye -xsen(xy)-
y

-
x
xy 2
1
f (x, y)=2ye -sen(xy)-yxcos(xy)-
y

-
x
yx 2
1
f (x, y)=2ye -sen(xy)-xycos(xy)-
y

-
2 x 2
xx
f (x, y)=y e -y cos(xy)
-
x 2
yy 3
2x
f (x, y)=2e -x cos(xy)+
y

Derivadas parciales sucesivas
Ejercicio

Calcular las derivadas parciales segundas de:


3 2 2 2 2
y
f(x, y)=x y - x + x tg( ) + x +y
x
.

Derivadas parciales sucesivas
En el ltimo ejemplo se verificaba que
xy yx
f =f , igualdad que en general no es cier-
ta, aunque si lo ser para la mayora de funciones que manejemos.

Una condicin suficiente para que
xy yx
f =f , la da el:

Teorema (de Schwarz, sobre la permutabilidad de orden de derivacin)
Si f est definida en un entorno U de (a, b), y si existen las derivadas parciales f
x
, f
y
,
f
xy
en el mismo U, siendo tambin f
xy
continua en (a, b) , entonces existe f
yx
(a, b) y
se cumple
xy yx
f (a, b)=f (a, b) .

Para ms de dos variables el concepto de derivada parcial es anlogo. Veamos un
ejemplo para tres variables

Ejemplo

Calcular la derivadas parciales primeras de

f(x, y, z) = x
2
+y
2
+z
2
+e
xyz

xyz
x
xyz
y
xyz
z
f (x,y,z)=2x+yze
f (x,y,z)=2y+xze
f (x,y,z)=2z+xye

Derivadas parciales sucesivas
Regla de la cadena
Estudiemos ahora la regla de la cadena o la derivada de la funcin compuesta para
funciones de dos variables.

Regla de la cadena para el caso: z = f(x, y), x = g(t), y = h(t).

Teorema
Sea z = f(x, y) diferenciable en (x, y). Si x = g(t), y = h(t), siendo g y h funciones de-
rivables en t, entonces f es derivable en t, y su derivada es

z(t) = z
x
x(t) + z
y
y(t).
Ejemplo

Siendo z = xy
2
x
2
, con x = cos t, y = sen t verificamos el resultado anterior calcu-
lando z(t) de dos formas distintas: directamente sustituyendo x, y en funcin de t
y, aplicando el teorema anterior:

z = cos t sen
2
t cos
2
t z

= -sen t sen
2
t + 2cos t cos t sen t + 2sen t cos t =
= -sen
3
t + 2cos
2
t sen t + 2sen t cos t

z(t) = z
x
x(t) + z
y
y(t) = (y
2
2x)(- sen t) + 2xy cos t = (sen
2
t 2 cos t)(- sen t) +
+ 2 cos
2
t sen t, que coincide con el resultado anterior.
z
z
x
z
y
x y
t
t
x(t)
y(t)
Regla de la cadena
z = f(x, y), x = g(t), y = h(t).
z(t) = z
x
x(t) + z
y
y(t)
Regla de la cadena
Regla de la cadena para el caso: z = f(x, y), x = g(u, v), y = h(u, v)):

Teorema

Si f es diferenciable en (x, y), existen las derivadas parciales x
u
, x
v
, y
u
, y
v
en (u, v),
entonces existen z
u
, z
v
en (u, v) y se verifica:

z
u
= z
x
x
u
+ z
y
y
u

z
v =
z
x
x
v
+

z
y
y
v


Para funciones de mas de dos variables se obtienen resultados anlogos.

Ejercicio
Siendo
2 2
x y
z=
2
, x = u + v, y = u-v, calcular z
u
, z
v
de dos formas distintas:
a) Sustituyendo x e y en funcin de u y v.
b) Aplicando el teorema anterior.
x
y
z
z
x
z
y
u v
u
v
x
u
x
v
y
u
y
v
Regla de la cadena
z = f(x, y), x = g(u, v), y = h(u, v))
z
u
= z
x
x
u
+ z
y
y
u

z
v =
z
x
x
v
+

z
y
y
v

Derivacin en forma implicita
El modo de escribir la funcin de dos variables, hasta ahora, ha sido z = f(x,
y), y decimos que z est dada en forma explicita, es decir, despejada en fun-
cin de x, y.

Otra forma, mas general, de definir z como funcin de x, y es F(x, y, z) = 0,
que se llama forma implcita de definir z como funcin de x, y (la z no est
despejada).

El pasar de la forma explicita a la implcita es inmediato:

z = f(x, y) z f(x, y) = 0, llamando F(x, y, z) = z f(x, y) F(x, y, z) = 0

El pasar de la forma implcita a la explicita, en general, es mas complicado, y
a veces, es imposible como se ve con el ejemplo z
5
x
2
+ z
3
y sen xy = 0.

Supongamos que z est definida implcitamente como funcin de x e y:
F(x, y, z) = 0, considerando F como una funcin de tres variables: x, y, z, si
aplicamos la regla de la cadena a la igualdad F(x, y, z) = 0 , se obtiene:

derivando respecto de x :
F
x
x
x
+F
y
y
x
+F
z
z
x
= 0, siendo x
x
=1, y
x
=0
x
x
z
-F
z =
F

derivando respecto de y :
F
x
x
y
+F
y
y
y
+F
z
z
y
= 0, siendo y
y
=1, x
y
=0
y
y
z
-F
z =
F

Ejemplo

Siendo z
3
sen x + ze
xy
xy = 0, obtener z
x
, z
y
aplicando el resultado anterior.
En este caso F(x, y, z) = z
3
sen x + ze
xy
xy, luego

F
x
= z
3
cos x + zye
xy
y, F
y
= zxe
xy
x, F
z
= 3z
2
sen x + e
xy
.

Por lo que sustituyendo queda:


3 xy
x 2 xy
-z cosx-zye +y
z =
3z sen x+e
,
xy
y 2 xy
-xze +x
z =
3z sen x+e

Derivacin en forma implicita
Ejercicio

Con el mismo dato del ejemplo anterior, obtener z
x
, z
y
derivando
directamente la igualdad z
3
sen x + ze
xy
xy = 0 , y considerando que
z es funcin de x e y. Comprobar que el resultado obtenido coincide
con el anterior.
Derivacin en forma implicita
Como otra aplicacin de la derivacin implcita, obtengamos la ecuacin de plano
tangente a al superficie z = f(x, y) en el punto P(a, b, c) cuando esta viene dada en
forma implcita F(x, y, z) = 0.
Se obtuvo que esta es:

z
x
(a, b)(x-a)+z
y
(a, b)(y-b)-(z-c) = 0

y siendo
x
x
z
-F
z =
F
,
y
y
z
-F
z =
F
sustituyendo queda:


y
x
z z
x y z
F (a,b,c)
-F (a,b,c)
(x-a)- (y-b)-(z-c)=0
F (a,b,c) F (a,b,c)
F (a,b,c)(x-a)+F (a,b,c)(y-b)+F (a,b,c)(z-c)=0

Luego la recta normal en el punto P(a, b, c) tiene como vector director
(F
x
(a, b, c), F
y
(a, b, c), F
z
(a, b, c)), por lo que su ecuacin en forma paramtrica es

x
y
z
x=a+tF (a,b,c)
y=b+tF (a,b,c)
z=c+tF (a,b,c)

)

Derivacin en forma implicita
Ejemplo
Obtener la ecuacin del plano tangente y de la normal a la superficie
x y
z z
2 +2 =8 ,
en el punto P(2, 2, 1).
En este caso es F(x, y, z) =
x y
z z
2 +2 - 8 , calculamos las derivadas parciales:

x y x y
z z z z
x y z
2 2
1 1 x y
F =log2 2 , F =log2 2 , F =-log2 2 -log2 2
z z z z
.

Tomando valores en P:
x y z
F (2,2,1)=4log2, F (2,2,1)=4log2, F (2,2,1)=-8log2-8log2=-16log2 .

Como consecuencia la ecuacin del plano tangente en P es

4log2(x-2)+4log2(y-2)-16log2(z-1) = 0 x-2+y-2-4z+4 = 0 x+y-4z = 0.

La ecuacin de la recta normal es

x=2+t
y=2+t
z=1-4t

)

Derivacin en forma implicita
Ejercicio

Obtener las ecuaciones del plano tangente y de la recta normal a la
superficie:

z
2
+4z+x
2
= 0, en los puntos de interseccin con el eje OZ.
Derivacin en forma implcita