Frequency Distribution

Convert raw data into a data array.

Construct:
a frequency distribution.
a relative frequency distribution.
a cumulative relative frequency distribution.
Construct different types of diagrams.
Visually represent data by using graphs
and charts.

Data array
An orderly presentation of data in either
ascending or descending numerical order.
Frequency Distribution
A table that represents the data in classes and
that shows the number of observations in
each class.
Frequency Distribution
Class - The category
Frequency - Number in each class
Cum frequency: Number UP To the class
Class limits - Boundaries for each class
Class interval - Width of each class
Class mark - Midpoint of each class


Two methods of grouping
Exclusive: example- 0-9.99, 10-19.99,
20-29.99 ..

Inclusive: example- 0-10, 10.01- 20
20.01-30 and so on..
Both are correct
Sturges rule
As such NO RIGID RULE
Classes normally are : 5 to 15 depending on the
data
How to set the approximate number of classes
to begin constructing a frequency distribution.
K= 1+ 3.322 log N
Class Interval= Range/ K


where K = approximate number of classes to use and
N = the number of observations in the data set .

Precautions
No uneven classes
Avoid odd upper limits
Avoid odd interval
All values should have a unique class
Test
Which type of data is better?
Grouped or ungrouped
WHY ?
How to Construct a
Frequency Distribution
. Number of classes
Choose an approximate number of classes for your data.
Sturges rule can help.
2. Estimate the class interval
Divide the approximate number of classes (from Step 1)
into the range of your data to find the approximate class
interval, where the range is defined as the largest data
value minus the smallest data value.
3. Determine the class interval
Round the estimate (from Step 2) to a convenient value.


Lower Class Limit
Determine the lower class limit for the first class by
selecting a convenient number that is smaller than the
lowest data value.
5. Class Limits
Determine the other class limits by repeatedly adding
the class width (from Step 2) to the prior class limit,
starting with the lower class limit (from Step 3).
6. Define the classes
Use the sequence of class limits to define the classes
Converting to a Relative
Frequency Distribution
Retain the same classes defined in the
frequency distribution.
2. Sum the total number of observations
across all classes of the frequency
distribution.
3. Divide the frequency for each class by the
total number of observations, forming the
percentage of data values in each class
Example: Problem
The average daily cost to community hospitals
for patient stays during 1993 for each of the 50
U.S. states was given in the next table.
a) Arrange these into a data array.

*) Approximately how many classes would be
appropriate for these data?
c & d) Construct a frequency distribution. State
interval width and class mark.
e) Construct a histogram, a relative frequency
distribution, and a cumulative relative frequency
distribution.

Data
AL $775 HI 823 MA 1,036 NM 1,046 SD 506
AK 1,136 ID 659 MI 902 NY 784 TN 859
AZ 1,091 IL 917 MN 652 NC 763 TX 1,010
AR 678 IN 898 MS 555 ND 507 UT 1,081
CA 1,221 IA 612 MO 863 OH 940 VT 676
CO 961 KS 666 MT 482 OK 797 VA 830
CT 1,058 KY 703 NE 626 OR 1,052 WA 1,143
DE 1,024 LA 875 NV 900 PA 861 WV 701
FL 960 ME 738 NH 976 RI 885 WI 744
GA 775 MD 889 NJ 829 SC 838 WY 537
Step 1. Number of classes
Sturges Rule: approximately 7 classes.
The range is: $1,221 $482 = $739
$739/7 = $106 and $739/8 = $92
Steps 2 & 3. The Class Interval
So, if we use 8 classes, we can make each
class $100 wide.


Step 4. The Lower Class Limit
If we start at $450, we can cover the range in 8
classes, each class $100 in width.
The first class : $450 up to $550
Steps 5 & 6. Setting Class Limits
$450 up to $550 $850 up to $950
$550 up to $650 $950 up to $1,050
$650 up to $750 $1,050 up to $1,150
$750 up to $850 $1,150 up to $1,250

Average daily cost Number Mark
$450 under $550 4 $500
$550 under $650 3 $600
$650 under $750 9 $700
$750 under $850 9 $800
$850 under $950 11 $900
$950 under $1,050 7 $1,000
$1,050 under $1,150 6 $1,100
$1,150 under $1,250 1 $1,200

Interval width: $100

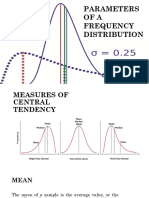
Measures of Central Tendency
and Dispersion
Introduction

Raw Data are the raw materials that will have to
be converted into finished products (Information).
From a voluminous database containing raw data,
it is impossible to see any pattern unless they are
converted into information by data reduction. The
reduction can be achieved by summary measures,
which are concise and yet give a reasonably
accurate view of the original data. Here we cover
the important summary measures of central
tendency and dispersion (variation)

Outline
1) What is Central Tendency?

2) Measures of Central Tendency

3) Measures of Dispersion

1) What is Central Tendency?
Whenever you measure things of the same
kind, a fairly large number of such
measurements will tend to cluster around the
middle value. The question that arises is " is it
possible to define one typical representative
average in such a manner that the remaining
items in the data set will cluster around this
value?" will have a tendency to be closer to
this value? Such a value is called a measure of
"Central Tendency". The other terms that are
used synonymously are "Measures of
Location", or "Statistical Averages".
2) Measures of Central
Tendency
Quantitative Specialists, Statisticians, and
Information Analysts rely heavily on summary
measures when a large mass of data will have to
be analyzed to help decision-makers. As a
manager, You need these summary measures of
central tendency to draw meaningful conclusions in
your functional area of operation. The most widely
used measures of central tendency are
Arithmetic Mean, Median, and Mode.

Arithmetic Mean
Arithmetic Mean (called mean) is the most common
measure of central tendency used by all managers in their
sphere of activities. It is defined as the sum of all
observations in a data set divided by the total number of
observations. For example, consider a data set containing
the following observations:

4, 3, 6, 5, 3, 3. The arithmetic mean =
(4+3+6+5+3+3)/6 =4. In symbolic form mean is given
by


= Arithmetic Mean

= Indicates sum all X values in the data set

= Total number of observations(Sample Size)

n
X
X

=
X

X
n

Arithmetic Mean for Raw Data
Example
The inner diameter of a particular grade of tire based
on 5 sample measurements are as follows: (figures in
millimeters)

565, 570, 572, 568, 585

Applying the formula


We get mean = (565+570+572+568+585)/5 =572

Caution: Arithmetic Mean is affected by extreme values
or fluctuations in sampling. It is not the best average to
use when the data set contains extreme values (Very
high or very low values).


n
X
X

=

Median
Median is the middle most observation when you arrange data
in ascending or descending order of magnitude. That is, the
data are ranked and the middle value is picked up. Median is
such that 50% of the observations are above the median and
50% of the observations are below the median.

Median is a very useful measure for ranked data in the context
of consumer preferences and rating. It is not affected by
extreme values but affected by the number of observations.

th value of ranked data

n = Number of observations in the sample

Note: If the sample size is an odd number then median is
(n+1)/2 th value in the ranked data. If the sample size is even,
then median will be between two middle values. You take the
average of these two middle values.


2
1 n
Median
+
=
Median for Raw Data
Example -Odd Sample Size
Marks obtained by 7 students in Computer Science
Exam
are given below: Compute the median.

45 40 60 80 90 65 55

Arranging the data after ranking gives

90 80 65 60 55 45 40

Median = (n+1)/2 th value in this set = (7+1)/2 th
observation= 4
th
observation=60
Hence Median = 60 for this problem.

Median for Raw Data
Example - Even Sample Size
Diameter of a shaft in millimeters in a manufacturing unit is
Given below for 10 samples. Calculate the median value.

2.50 2.45 2.55 2.60 2.46 2.43 2.56 2.58
2.66 2.65

Arranging the data in the ascending order, you will get

2.43 2.45 2.46 2.50 2.55 2.56 2.58 2.60
2.65 2.66

The median falls between 5th and 6th observation. That is
between 2.55 and 2.56. Hence median = (2.55+2.56)/2
=2.555

Mode
Mode is that value which occurs most often. It has the
maximum frequency of occurrence. Mode is not affected
by extreme values.

Mode is a very useful measure when you want to keep in
the inventory, the most popular shirt in terms of collar
size during festival season. Median and mean will not be
helpful in this type of situation. Another example where
mode is the only answer is in determining the most
typical shoe size to be kept in stock in a shop selling
shoes.

Caution: In a few problems in real life, there will be more
than one mode such as bimodal and multi-modal values.
In these cases mode cannot be uniquely determined.

Mode for Raw Data
Example
The life in number of hours of 10 flashlight batteries are as
follows: Find the mode.
340 350 340 340 320 340 330 330
340 350

340 occurs five times. Hence, mode=340.




Mean for Grouped Data

Formula for Mean is given by

Where

= Mean



= Sum of cross products of frequency in each class
with midpoint X of each class


n = Total number of observations (Total frequency) =
n
fX
X

=
X

fX

f
Mean for Grouped Data
Example
Find the arithmetic mean for the following
continuous
frequency distribution:

Class 0-1 1-2 2-3 3-4 4-5 5-6
Frequency 1 4 8 7 3 2

Solution for the Example













Applying the formula =75.5/25=3.02
A B C D
1 Class X f fX
2 0-1 0.5 1 0.5
3 1-2 1.5 4 6.0
4 2-3 2.5 8 20.0
5 3-4 3.5 7 24.5
6 4-5 4.5 3 13.5
7 5-6 5.5 2 11.0
8 Totals 25 75.5
9 Mean 3.02

n
fX
X

=
Mean by short cut method
Where A is Assumed value ( one can assume any
value)
d is the deviation of each mid-value from A. If d=
( XA)/ c , then in the formula the second term
is multiplied by c. Where c is the class interval.
n
fd
X

+ = A
Assignment: find the mean using short-cut method
Example of short cut method
Table here presents
the profit of 1400
companies .Find the
mean using two
different methods

Profit No. of cos.
200-400 500
400-600 300
600-800 280
800-1000 120
1000-1200 100
1200-1400 80
1400-1600 20
Total 1400
Profit (f)Fr
eq.
(X)Mid
Point
(f X) d=
(X-A) /c
f d
200-400 500 300 150,000 -3 -1500
400-600 300 500 150,000 -2 -600
600-800 280 700 196,000 -1 -280
800-1000 120 900 108,000 0 0
1000-1200 100 1100 110,000 1 100
1200-1400 80 1300 104,000 2 160
1400-1600 20 1500 30,000 3 60
Total 1400 848,000 0 -2060

Direct method n
fX
X

=
714 . 605 1400 / 000 , 48 , 8 X = =
Short cut method
n
fd
X

+ = A
= 900 +(- 2060)(200)/ 1400=900-294.28
= 605.714
Properties of Mean
Sum of deviations from mean is always
zero.
Sum of squared deviation from Mean is
Minimum
If X= X1 + X2, Then the Mean of X is
equal to the sum of means of X1 and X2
(If the observations are equal)
From two or more groups a pooled
mean can be calculated

Median for Grouped
Data
Formula for Median is given by

Median =

Where
L =Lower limit of the median class
n = Total number of observations =
m= Cumulative frequency preceding the median class
f= Frequency of the median class
c= Class interval of the median class
c
f
m (n/2)
L

f
Median for Grouped Data
Example
Find the median for the following continuous
frequency distribution:

Class 0-10 11-20 21-30 31-40 41-50
Frequency 5 8 13 7 7

Solution for the Example
Class Frequency Cumulative
Frequency
0-10 5 5
11-20 8 13
21-30 13 26
31-40 7 33
41-50 7 40
Total 40
Substituting in the formula the relevant values,

Median = ,we have Median =

= 21+(70/13)= 21+5.38 = 26.38

c
f
m (n/2)
L

+
10
13
13 ) 2 / 40 (
21

+
Mode for Grouped Data

Mode =

Where L =Lower limit of the modal class


= Frequency of the modal class

= Frequency preceding the modal class

= Frequency succeeding the modal class

C = Class Interval of the modal class

c
d d
d
L
2 1
1

+
+
0 1 1
f f d =
2 1 2
f f d =
1
f
0
f
2
f
Mode for Grouped Data
Example
Example: Find the mode for the following
continuous frequency distribution:

Class 0-1 1-2 2-3 3-4 4-5 5-6
Frequency 1 4 8 7 3 2


Solution for the Example
Class Frequency
0-1 1
1-2 4
2-3 8
3-4 7
4-5 3
5-6 2
Total 25

Mode =

L = 2
= 8-4 = 4

= 8-7 = 1

C = 1 Hence Mode =
= 2.8


c
d d
d
L
2 1
1

+
+
0 1 1
f f d =
2 1 2
f f d =
1
5
4
2 +
Class assignment
Find the Median and Mode for the following data (
salary structure of 1500 employees)
( Answer Median= 33.46, Mode= 29.5)
Age 18-
22
22-
26
26-
30
30-
34
34-
38
38-
42
42-
46
46-
50
50-
54
54-
58
Fre
q
120 125 280 260 155 184 162 86 75 53
Comparison of
Mean, Median, Mode
Mean Median Mode
Defined as the arithmetic
average of all observations
in the data set.


Requires measurement on
all observations.


Uniquely and
comprehensively defined.

Defined as the
middle value in the
data set arranged
in ascending or
descending order.

Does not require
measurement on all
observations

Cannot be
determined under
all conditions.

Defined as the most
frequently occurring
value in the distribution;
it has the largest
frequency.

Does not require
measurement on all
observations

Not uniquely defined for
multi-modal situations.


Comparison of
Mean, Median, Mode Cont.
Mean Median Mode
Affected by extreme
values.


Can be treated
algebraically. That is,
Means of several groups
can be combined.
Not affected by
extreme values.

Cannot be treated
algebraically. That is,
Medians of several
groups cannot be
combined.
Not affected by
extreme values.

Cannot be treated
algebraically. That is,
Modes of several
groups cannot be
combined.

Which central tendency to use
Type of data:
If data is badly skewed: Avoid the Mean
If gaps in the data: Avoid median
If uneven frequencies: Avoid Mode
Purpose of Analysis:
Representative value: Mean
Qualitative/ nominal variable: Mode
Partition point: Median
Which central tendency to use
Frequency distribution:
Open ended classes: Median or Mode
(except certain situations)
Others : Mean
Nature of data:
Time series data: Avoid Mean
Ratios/rates : Avoid Mean
Relationship
Mean, Median and mode are related as
follows:
(Mean Mode)= 3 ( Mean Median)
For a completely symmetric distribution,
( Normal distribution) , the three
measures coincide with each other.
Fractiles / Quantiles
A FRACTILE is the value of an
observation which is located at a specified
place in a series of data. For example :
Median, which is located in the middle.
Various fractiles used are : Quartiles,
Deciles, Percentiles.
Median is 50
th
percentile or 5
th
decile or
2
nd
quartile.

How to calculate fractile values
Qn= P 25 n=
c
f
m (nN/4)
L

+
D n= P 10 n=
c
f
m (nN/10)
L

+
Class assignment: Calculate the fractiles from the
data
Age 18-
22
22-
26
26-
30
30-
34
34-
38
38-
42
42-
46
46-
50
50-
54
54-
58
Fre
q
120 125 280 260 155 184 162 86 75 53
3) Measures of Dispersion
In simple terms, measures of dispersion indicate
how large the spread of the distribution is
around the central tendency. It answers
unambiguously the question " What is the
magnitude of departure from the average value
for different groups having identical averages?".
It is important to study the central tendency
along with dispersion to throw light on the
shape of the curve; to gauge whether there is
distortion to the bell shaped symmetrical normal
distribution curve that forms the foundation
stone upon which the entire statistical inference
is built.


Range
Range is the simplest of all measures of dispersion. It is
calculated as the difference between maximum and
minimum value in the data set.

Range =

Example for Computing Range

The following data represent the percentage return on
investment for 10 mutual funds per annum. Calculate
Range.

12, 14, 11, 18, 10.5, 11.3, 12, 14, 11, 9

Range = = 18-9=9


Minimum Maximum
X X
Minimum Maximum
X X
Range is an absolute measure and is defined
for a particular data set. It can not be used
for comparison of two data sets.
Coefficient of Range is an absolute measure
Coefft. Of Range= ( LS)/ ( L+ S)
If its a small value, dispersion is less
Coeftt. Of Range is not a consistent measure,
thus it is not used always.
Example : two samples : first with extreme values
as 1 and 2 , the second sample having extreme
values as
11 and 12. these samples coefficient of range will
be First sample :(2-1)/(2+1)= 1/3 , second
sample:( 12-11)/ (12+11)=1/23



Range
Caution: Range is a good measure of spread in the
distribution only when a data set shows a stable
pattern of variation without extreme values. If one
of the components of range namely the maximum
value or minimum value becomes an extreme
value, then range should not be used.

Interquartile
Range
Range is entirely dependent on maximum and
minimum values in the data set and is highly
misleading when one of them is an extreme value.
To overcome this deficiency, you can resort to
interquartile range. It is computed as the range
after eliminating the highest and lowest 25% of
observations in a data set that is arranged in
ascending order. Thus this measure is not
sensitive to extreme values.

Interquartile range = Range computed on middle
50% of the observations

Interquartile Range-Example
The following data represent the percentage return
on investment for 9 mutual funds per annum.
Calculate interquartile range.

Data Set: 12, 14, 11, 18, 10.5, 12, 14, 11, 9
Arranging in ascending order, the data set becomes

9, 10.5, 11, 11, 12, 12, 14, 14, 18

Ignore the first two (9, 10.5) and last two (14, 18)
observations in this data set. The remaining contains
50% of the data. They are 11, 11, 12, 12, 14, and
14. For this if you calculate range, you get
interquartile range.
Interquartile range = 14-11 =3.

Quartile Deviation
Quartile deviation= IQR/2
This is an absolute measure of dispersion,
not to be used for comparison
For comparison we use Coefficient of
Quartile deviation
Coefft. Of QD = ( Q3Q1)/( Q3 +Q1)
Mean Absolute Deviation(MAD)
Mean Absolute Deviation (MAD) is defined as the average based on the
deviations measured from arithmetic mean, in which all deviations are
treated as positive ignoring the actual sign. Unlike range, MAD is based
on all observations. Hence it reflects the dispersion of every item in the
distribution. In symbolic form, it is defined by the following formula.

MAD =

Where

represents sum of all deviations from arithmetic mean
after ignoring sign

= Arithmetic Mean
n = Number of observations in the sample(sample size)

Caution: Mean Absolute Deviation (MAD) has two weaknesses. 1) It
cannot be combined for several groups. 2) Ignoring the sign has serious
implications to a business manager attempting to measure the spread of
the distribution in a scientific manner.


n
X X

X X
X
Example for MAD
The following data represent the percentage return on
investment for 10 mutual funds per annum. Calculate MAD
(Please note that this is the same example used for computing
Range)
12, 14, 11, 18, 10.5, 11.3, 12, 14, 11, 9
= (12+14+11+18+10.5+11.3+12+14+11+9)/10
=12.28

= + + +

+ + + +

+ + = 18.32
MAD = = 18.32/10 =1.832

n
X
X

=

X X 28 . 12 12
28 . 12 14
28 . 12 11
28 . 12 18
28 . 12 5 . 10 28 . 12 3 . 11
28 . 12 12
28 . 12 14
28 . 12 11 28 . 12 9
n
X X

Standard Deviation
Standard deviation forms the basis for the discussion on
Inferential Statistics. It is a classic measure of dispersion. It
has many advantages over the rest of the measures of
variations. It is based on all observations. It is capable of
being algebraically treated which implies that you can
combine standard deviations of many groups. It plays a very
vital role in testing hypotheses and forming confidence
interval.

To define standard deviation, you need to define another
term called variance. In simple terms, standard deviation is
the square root of variance.
Important Terms with Notations
Important Terms with notations

Key Remarks

Sample Variance
1
) (
2
2

n
X X
S

Sample Standard Deviation
S=
1
) (
2

n
X X

Population Variance
o
2
=
N
X

2
) (

Population Standard Deviation
= o
N
X

2
) (

Where
n
X
X

=
(Sample Mean) and
N
X

=
(Population Mean)
n =Number of observations in the
sample(Sample size)
N =Number of observations in the
Population (Population Size)


1.
1
) (
2
2

n
X X
S
is an unbiased
estimator of o
2
=
N
X

2
) (

2.
n
X
X

=
is an unbiased
estimator of
N
X

=

3. The divisor n-1 is always used
while calculating sample variance
for ensuring property of being
unbiased

4. Standard deviation is always the
square root of variance

Example for Standard
Deviation
The following data represent the percentage
return on investment for 10 mutual funds per
annum. Calculate the sample standard deviation.

12, 14, 11, 18, 10.5, 11.3, 12, 14, 11, 9

Solution for the Example
for the Example
Solution for the Example
Cont.
From the spreadsheet of Microsoft Excel in the previous slide,
it is easy to see

that Mean = =12.28 (In column A and row14, 12.28 is
seen).


Sample Variance = =6.33 (In column D and
row 14, 6.33 is seen)

Sample Standard Deviation = S = = 2.52
(In column D and row 15, 2.52 is seen)

n
X
X

=
1 n
) X (X
S
2
2

1 n
) X (X
2

Standard Deviation for

Grouped Data
The standard deviation for sample data, based on
frequency distribution is given by

S = which is used to estimate the
Population Standard Deviation .

Here

n is the Sample Size = , X =Mid Point of each class
2
2
] [
n
d
n
d


n
fX
X

=

f
Standard Deviation for
Grouped Data-Example
Frequency Distribution of Return on Investment of
Mutual Funds
Return on
Investment
Number of Mutual
Funds
5-10
10-15
15-20
20-25
25-30
Total
10
12
16
14
8
60
Solution for the Example
Solution for the Example
From the spreadsheet of Microsoft Excel in the
previous
slide, it is easy to see

Mean = =1040/60=17.333(cell F10),


Standard Deviation = S = =
= 6.44
(Cell H12)
n
fX
X

=
X
2
n
X
2

59
2448.33
Calculation of SD : Raw data
First the direct
method
Without deviation
method


Assumed mean
method

X
2
n
X
2

2
2
] [
n
d
n
d


1 n
) X (X
2

Calculation of SD : Grouped
First the direct
method


Without deviation
method


Assumed mean
method


1 n
) X f(X
2

X
2
n
fX
2

2
2
] [
n
f d
n
f d


Class assignment
Find the average
deviation and
standard deviation of
the following data:

Sales No. of shops
10-20 3
20-30 6
30-40 11
40-50 3
50-60 2
Solution: Mean= 825 / 25 = 33
Sales f X fx (X-33) f (X-33) Sqr F(sqr)
10-20 3 15 45 18 54 324 972
20-30 6 25 150 8 48 64 384
30-40 11 35 385 2 22 4 44
40-50 3 45 135 12 36 144 432
50-60 2 55 110 22 44 484 968
Total 25 825 204 2800
AD= 204/ 25=8.16, Variance= 2800 / 25=122, SD= 10.58
Class Assignment :SD from Assumed mean
Use the above
method to find the SD
of the following data
of 79 students

Marks No. of
students
0-10 18
10-20 16
20-30 15
30-40 12
40-50 10
50-60 5
60-70 2
70-80 1
deviation d= (XA)/ c , A= 25
Class X f fx X^2 fX^2 d fd d^2 fd^2
0-10 5 18 90 25 450 -2 -36 4 72
10-20 15 16 240 225 3600 -1 -16 1 16
20-30 25 15 375 625 9375 0 0 0 0
30-40 35 12 420 1225 14700 1 12 1 12
40-50 45 10 450 2025 20250 2 20 4 40
50-60 55 5 275 3025 15125 3 15 9 45
60-70 65 2 130 4225 8450 4 8 16 32
70-80 75 1 75 5625 5625 5 5 25 25
Total 79 2055 17000 77575 8 242
Deviation method
SD= 10 [ (242/ 79)( 8/79)(8/79)]^ 1/2
SD = 10 ( 1.75)= 17.5
Direct method
V= [ ( 77575/ 79)(2055/79)( 2055/79)]
SD= {981.96676.75}^1/2= { 303.3}^1/2
=17.47

ns observatio the of 50% covers Q.D. X
on distributi symmetric a In
D A.
Q.D.
dispersion of measures other and S.D between ip Relationsh

o =
o =
o
o

5
4
3
2

ns observatio the of % 68.26 covers S.D

ns observatio the of 57.5% covers A.D
X
X
Coefficient of Variation
(Relative Dispersion)
Coefficient of Variation (CV) is defined as the ratio of
Standard Deviation to Mean.
In symbolic form

CV= for the sample data and = for the
population data.

CV is the measure to use when you want to see the
relative spread across groups or segments. It also
measures the extent of spread in a distribution as a
percentage to the mean. Larger the CV, greater is the
percentage spread. As a manager, you would like to have
a small CV so that your assessment in a situation is
robust. The percentage risk is minimized.

X
S

Coefficient of Variation
Example
Consider two Sales Persons working in the same
territory. The sales performance of these two in the
context of selling PCs are given below. Comment on the
results.



Sales Person 1 Sales Person 2
Mean Sales (One year
average) 50 units

Standard Deviation
5 units
Mean Sales (One year
average)75 units

Standard deviation
25 units

Interpretation for the Example
The CV is 5/50 =0.10 or 10% for the Sales Person1
and 25/75=0.33 or 33% for sales Person2. It
seems Sales Person1 performs better than Sales
Person2 with less relative dispersion or scattering.
Sales Person2 has a very high departure or
standard deviation from his average sales
achievement. The moral of the story is "don't get
carried away by absolute number". Look at the
scatter. Even though, Sales Person2 has achieved a
higher average, his performance is not consistent
and seems erratic.


Example:Coefficient of Variation

Since Mean and variance are enough
to compare two groups of data CV is
used to measure the relative spread of
the data
Two factories which have 50 and 100
employees have the average wages as
Rs.120 per day and Rs. 85 per day.
The variance of wages in the two
factories are 9 and 16 respectively.
Find which factory has more uniformity
in wages?
CV for factory A = 3/120x 100= 2.5
CV for factory B= 4/85x 100= 4.7
Factory A has more uniform wages

Skewness
Measure of asymmetry of a frequency distribution
Skewed to left
Symmetric or unskewed
Skewed to right
Kurtosis
Measure of flatness or peakedness of a frequency
distribution
Platykurtic (relatively flat)
Mesokurtic (normal)
Leptokurtic (relatively peaked)
Skewness and Kurtosis
Skewed to left
Skewness
Skewness
Symmetric
Skewness
Skewed to right
Kurtosis
Platykurtic - flat distribution
Kurtosis
Mesokurtic - not too flat and not too peaked
Kurtosis
Leptokurtic - peaked distribution
Skewness
(i) Mean-Mode/S.D
(ii) 3(Mean-Median)/S.D
(iii) Bowleys :
BS= (Q3+Q1-2 Median)/(Q3-A1)
Kelleys:
KS= P50-(P10+P90)/2
BASED ON MOMENTS
BETA1= (Mu3)^2/ (Mu2)^3
Kurtosis
Kurtosis is measured by Beta2
Beta2= (Mu4)/ (Mu2)^2

Where Mu2= (1/N) Sum(X-mean)^2
And Mu4= (1/N) Sum (X-Mean)^4
Kurtosis
PlatyKurtic : Flat
Mesokurtic: Normal
Leptokurtic: Very high
Beta2= Mu4/(Mu2)^2
Where Mu4= 1/n( Sum fd^4)
and Mu2= 1/n( Sum fd^2)
Chebyshevs Theorem
Applies to any distribution, regardless of shape
Places lower limits on the percentages of
observations within a given number of standard
deviations from the mean
Empirical Rule
Applies only to roughly mound-shaped and
symmetric distributions
Specifies approximate percentages of observations
within a given number of standard deviations from
the mean
Relations between the Mean
and Standard Deviation
1
1
2
1
1
4
3
4
75%
1
1
3
1
1
9
8
9
89%
1
1
4
1
1
16
15
16
94%
2
2
2
= = =
= = =
= = =
At least of the elements of
any distribution lie within k standard
deviations of the mean
At
least
Lie
within
Standard
deviations
of the mean
2

3

4
Chebyshevs Theorem
|
.
|

\
|

2
1
1
k
For roughly mound-shaped and
symmetric distributions,
approximately:
68% 1 standard deviation
of the mean

95% Lie
within
2 standard deviations
of the mean

All 3 standard deviations
of the mean


Empirical Rule
Pie Charts
Categories represented as percentages of total
Bar Graphs
Heights of rectangles represent group frequencies
Frequency Polygons
Height of line represents frequency
Ogives
Height of line represents cumulative frequency
Time Plots
Represents values over time
1-8 Methods of Displaying Data
Pie Chart
Bar Chart
Average Revenues

Average Expenses
Fig. 1-11 Airline Operating Expenses and Revenues
1 2
1 0
8
6
4
2
0
A i r l i n e
American Continental Delta Northwest Southwest United USAir
Relative Frequency Polygon
Ogive
Frequency Polygon and Ogive
5 0 4 0 3 0 2 0 1 0 0
0 . 3
0 . 2
0 . 1
0 . 0
Sales
5 0 4 0 3 0 2 0 1 0 0
1 . 0
0 . 5
0 . 0
Sales
O S A J J M A M F J D N O S A J J M A M F J D N O S A J J M A M F J
8 . 5
7 . 5
6 . 5
5 . 5
M o n t h
M

i
l
l
i
o
n
s

o
f

T

o
n
s

M o n t h l y S t e e l P r o d u c t i o n
( P r o b l e m 1 - 4 6 )
Time Plot
Stem-and-Leaf Displays
Quick-and-dirty listing of all observations
Conveys some of the same information as a histogram
Box Plots
Median
Lower and upper quartiles
Maximum and minimum
Techniques to determine relationships and
trends, identify outliers and influential
observations, and quickly describe or
summarize data sets.
1-9 Exploratory Data Analysis -
EDA

1 122355567
2 0111222346777899
3 012457
4 11257
5 0236
6 02

Example 1-8: Stem-and-Leaf
Display

X X
* o
Median
Q
1
Q
3 Inner
Fence
Inner
Fence
Outer
Fence
Outer
Fence
Interquartile Range
Smallest data
point not
below inner
fence
Largest data
point not
exceeding inner
fence
Suspected
outlier Outlier
Q
1
-3(IQR)
Q
1
-1.5(IQR) Q
3
+1.5(IQR)
Q
3
+3(IQR)
Elements of a Box Plot
Box Plot
Example: Box Plot
1-10 Using the Computer The
Template Output
Using the Computer Template
Output for the Histogram
Using the Computer Template
Output for Histograms for
Grouped Data
Using the Computer Template Output for Frequency
Polygons & the Ogive for Grouped Data
Using the Computer Template Output for Two
Frequency Polygons for Grouped Data
Using the Computer Pie
Chart Template Output
Using the Computer Bar
Chart Template Output
Using the Computer Box Plot
Template Output
Using the Computer Box Plot
Template to Compare Two
Data Sets
Using the Computer Time
Plot Template
Using the Computer Time
Plot Comparison Template