Beruflich Dokumente
Kultur Dokumente
AR231 عزم القصور - Chap08 - MomentofInertia
Hochgeladen von
Ahmed El MorsyOriginalbeschreibung:
Originaltitel
Copyright
Verfügbare Formate
Dieses Dokument teilen
Dokument teilen oder einbetten
Stufen Sie dieses Dokument als nützlich ein?
Sind diese Inhalte unangemessen?
Dieses Dokument meldenCopyright:
Verfügbare Formate
AR231 عزم القصور - Chap08 - MomentofInertia
Hochgeladen von
Ahmed El MorsyCopyright:
Verfügbare Formate
IZMIR INSTITUTE OF TECHNOLOGY
8.0
09.12.2014
Department of Architecture
AR231 Fall12/13
SECOND MOMENT OR MOMENT OF INERTIA
OF AN AREA
8.1
Introduction
8.2
Moment of Inertia of an Area
8.3
Moment of Inertia of an Area by Integration
8.4
Polar Moment of Inertia
8.5
Radius of Gyration
8.6
Parallel Axis Theorem
8.7
Moments of Inertia of Composite Areas
8.8
Product of Inertia
8.9
Principal Axes and Principal Moments of Inertia
Dr. Engin Akta
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
8.1. Introduction
Forces which are proportional to the area or volume over which they act
but also vary linearly with distance from a given axis.
- the magnitude of the resultant depends on the first moment of the
force distribution with respect to the axis.
- The point of application of the resultant depends on the second
moment of the distribution with respect to the axis.
Herein methods for computing the moments and products of inertia for
areas and masses will be presented
09.12.2014
Dr. Engin Akta
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
8.2. Moment of Inertia of an
Area
Consider distributed forces F whose magnitudes are
proportional to the elemental areas A on which they
act and also vary linearly with the distance of A
from a given axis.
Example: Consider a beam subjected to pure bending.
Internal forces vary linearly with distance from the
neutral axis which passes through the section centroid.
F kyA
R k y dA 0
M k y 2 dA
y dA Qx first moment
2
y dA second moment
Example: Consider the net hydrostatic force on a
submerged circular gate.
F pA yA
R y dA
M x y 2 dA
09.12.2014
Dr. Engin Akta
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
8.3.Moment of Inertia of an Area by Integration
Second moments or moments of inertia of
an area with respect to the x and y axes,
I x y 2 dA
I y x 2 dA
Evaluation of the integrals is simplified by
choosing dA to be a thin strip parallel to
one of the coordinate axes.
For a rectangular area,
h
I x y dA y 2bdy 13 bh3
2
The formula for rectangular areas may also
be applied to strips parallel to the axes,
dI x 13 y 3dx
09.12.2014
Dr. Engin Akta
dI y x 2 dA x 2 y dx
4
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
8.4. Polar Moment of Inertia
The polar moment of inertia is an important
parameter in problems involving torsion of
cylindrical shafts and rotations of slabs.
J 0 r 2 dA
The polar moment of inertia is related to the
rectangular moments of inertia,
J 0 r 2 dA x 2 y 2 dA x 2 dA y 2 dA
I y Ix
09.12.2014
Dr. Engin Akta
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
8.5. Radius of Gyration of an Area
Consider area A with moment of inertia
Ix. Imagine that the area is
concentrated in a thin strip parallel to
the x axis with equivalent Ix.
I
I x k x2 A
kx x
A
kx = radius of gyration with respect
to the x axis
Similarly,
Iy
k y2 A
ky
J O kO2 A kO
Iy
A
JO
A
k O2 k x2 k y2
09.12.2014
Dr. Engin Akta
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
Examples
SOLUTION:
A differential strip parallel to the x axis is chosen for
dA.
dI x y 2dA
dA l dy
For similar triangles,
Determine the moment of
inertia of a triangle with respect
to its base.
l h y
b
h
l b
h y
h
dA b
h y
dy
h
Integrating dIx from y = 0 to y = h,
h y
bh 2
I x y dA y b
dy hy y 3 dy
h
h0
0
2
b y3 y 4
h
h 3
4
0
09.12.2014
Dr. Engin Akta
bh3
I x
12
7
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
SOLUTION:
An annular differential area element is chosen,
dA 2 u du
dJ O u 2 dA
r
J O dJ O u 2 u du 2 u 3du
2
JO
a) Determine the centroidal polar
moment of inertia of a circular
area by direct integration.
r4
From symmetry, Ix = Iy,
JO I x I y 2I x
b) Using the result of part a,
determine the moment of inertia
of a circular area with respect to a
diameter.
09.12.2014
r 4 2I x
I diameter I x r 4
4
Dr. Engin Akta
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
8.6. Parallel Axis Theorem
Consider moment of inertia I of an area A
with respect to the axis AA
I y 2 dA
The axis BB passes through the area centroid
and is called a centroidal axis.
I y 2 dA y d 2 dA
y 2 dA 2d y dA d 2 dA
I I Ad 2
09.12.2014
Dr. Engin Akta
parallel axis theorem
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
Moment of inertia IT of a circular area with
respect to a tangent to the circle,
I T I Ad 2 14 r 4 r 2 r 2
54 r 4
Moment of inertia of a triangle with respect to a
centroidal axis,
I AA I BB Ad 2
I BB I AA Ad
1 bh3
12
2
1
1
2 bh 3 h
1 bh3
36
09.12.2014
Dr. Engin Akta
10
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
8.7. Moments of Inertia of Composite Areas
The moment of inertia of a composite area A about a given axis is
obtained by adding the moments of inertia of the component areas
A1, A2, A3, ... , with respect to the same axis.
09.12.2014
Dr. Engin Akta
11
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
Example
225 mm
20 mm
358 mm
SOLUTION:
Determine location of the centroid of
composite section with respect to a
coordinate system with origin at the
centroid of the beam section.
Apply the parallel axis theorem to
determine moments of inertia of beam
section and plate with respect to
172 mm
composite section centroidal axis.
The strength of a W360x57 rolled steel
beam is increased by attaching a
Calculate the radius of gyration from the
225x20 mm plate to its upper flange.
moment of inertia of the composite
section.
Determine the moment of inertia and
radius of gyration with respect to an
axis which is parallel to the plate and
passes through the centroid of the
section.
09.12.2014
Dr. Engin Akta
12
IZMIR INSTITUTE OF TECHNOLOGY
225 mm
20 mm
Department of Architecture
AR231 Fall12/13
SOLUTION:
Determine location of the centroid of composite section
with respect to a coordinate system with origin at the
centroid of the beam section.
358 mm
172 mm
189 mm
A 225 mm 20 mm 4500 mm 2
1
1
y 358 mm 20 mm 189 mm
2
2
2 2
mm
Section
A, in
Plate
6.75
4500
7230
Beam Section 11.20
17.95
A 11730
Y A yA
09.12.2014
y , in.
mm
7189
.425
0
3 3
yA, inmm
50
.12 x 103
850.5
0
50.12 x 103
yA 850.5
yA 850.5 10
A 11730
Dr. Engin Akta
72.51 mm.
13
IZMIR INSTITUTE OF TECHNOLOGY
225 mm
20 mm
Department of Architecture
AR231 Fall12/13
Apply the parallel axis theorem to determine moments of
inertia of beam section and plate with respect to composite
section centroidal axis.
I x,beam section I x AY 2 160.2 106 723072.51
358 mm
198.2 104
I x,plate I x Ad 2 121 22520 4500189 72.51
3
61.2 106 mm4
172 mm
I x I x,beamsection I x,plate 192.6 106 61.2 106
I x 254 10 6 mm 4
189 mm
Calculate the radius of gyration from the moment of inertia
of the composite section.
k x
09.12.2014
I x 253.8 10 6 mm 4
A
11730 mm 2
Dr. Engin Akta
k x 147 .1 mm.
14
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
Example
SOLUTION:
Compute the moments of inertia of the
bounding rectangle and half-circle with
respect to the x axis.
The moment of inertia of the shaded area is
obtained by subtracting the moment of
inertia of the half-circle from the moment
of inertia of the rectangle.
Determine the moment of inertia
of the shaded area with respect to
the x axis.
09.12.2014
Dr. Engin Akta
15
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
SOLUTION:
Compute the moments of inertia of the bounding
rectangle and half-circle with respect to the x axis.
Rectangle:
I x 13 bh3 13 240 120 138.2 106 mm 4
Half-circle:
moment of inertia with respect to AA,
I AA 18 r 4 18 90 4 25.76 106 mm 4
moment of inertia with respect to x,
4r 4 90
a
38.2 mm
3
3
b 120 - a 81.8 mm
A 12 r 12 90
2
12.72 103 mm 2
09.12.2014
I x I AA Aa 2 25.76 106 12.72 103
7.20 106 mm 4
moment of inertia with respect to x,
I x I x Ab 2 7.20 106 12.72 103 81.82
92.3 106 mm 4
Dr. Engin Akta
16
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
The moment of inertia of the shaded area is obtained by
subtracting the moment of inertia of the half-circle from
the moment of inertia of the rectangle.
Ix
138.2 106 mm 4
92.3 106 mm 4
I x 45.9 106 mm4
09.12.2014
Dr. Engin Akta
17
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
8.8. Product of Inertia
Product of Inertia:
I xy xy dA
When the x axis, the y axis, or both are an
axis of symmetry, the product of inertia is
zero.
Parallel axis theorem for products of inertia:
I xy I xy xyA
09.12.2014
Dr. Engin Akta
18
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
8.9. Principal Axes and Principal Moments of Inertia
Given I x y 2 dA I y x 2 dA
I xy xy dA
we wish to determine moments
and product of inertia with
respect to new axes x and y.
Note: x x cos y sin
y y cos x sin
09.12.2014
The change of axes yields
Ix Iy Ix I y
I x
cos 2 I xy sin 2
2
2
Ix I y Ix I y
I y
cos 2 I xy sin 2
2
2
Ix Iy
I xy
sin 2 I xy cos 2
2
The equations for Ix and Ixy are the
parametric equations for a circle,
I x I ave 2 I x2y R 2
I ave
Ix I y
2
Ix I y 2
I xy
R
2
The equations for Iy and Ixy lead to the
same circle.
Dr. Engin Akta
19
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
At the points A and B, Ixy = 0 and Ix is
a maximum and minimum, respectively.
I max, min I ave R
tan 2 m
2 I xy
Ix I y
The equation for Qm defines two
angles, 90o apart which correspond to
the principal axes of the area about O.
I x I ave 2 I x2y R 2
I ave
09.12.2014
Ix I y
2
Ix I y 2
I xy
R
2
Imax and Imin are the principal moments
of inertia of the area about O.
Dr. Engin Akta
20
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
Example
SOLUTION:
Determine the product of inertia using
direct integration with the parallel axis
theorem on vertical differential area strips
Apply the parallel axis theorem to
evaluate the product of inertia with respect
to the centroidal axes.
Determine the product of inertia of
the right triangle (a) with respect
to the x and y axes and
(b) with respect to centroidal axes
parallel to the x and y axes.
09.12.2014
Dr. Engin Akta
21
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
SOLUTION:
Determine the product of inertia using direct integration
with the parallel axis theorem on vertical differential
area strips
x
x
y h1 dA y dx h1 dx
b
b
x
xel x
yel 12 y 12 h1
b
Integrating dIx from x = 0 to x = b,
b
I xy dI xy xel yel dA x
0
b
1
2
x
h 1 dx
b
x 2 x3 x 4
x
2 x x
h
dx h 2
2 b 2b 2
0
4 3b 8b 0
2
1 b2h2
I xy 24
09.12.2014
Dr. Engin Akta
22
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
Apply the parallel axis theorem to evaluate the
product of inertia with respect to the centroidal axes.
x 13 b
y 13 h
With the results from part a,
I xy I xy x yA
13 h12 bh
1 b2h2 1 b
I xy 24
3
1 b2h2
I xy 72
09.12.2014
Dr. Engin Akta
23
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
Example
SOLUTION:
Compute the product of inertia with
respect to the xy axes by dividing the
section into three rectangles and applying
the parallel axis theorem to each.
Determine the orientation of the
principal axes (Eq. 9.25) and the
principal moments of inertia (Eq. 9. 27).
For the section shown, the moments of
inertia with respect to the x and y axes
are Ix = 10.38 in4 and Iy = 6.97 in4.
Determine (a) the orientation of the
principal axes of the section about O,
and (b) the values of the principal
moments of inertia about O.
09.12.2014
Dr. Engin Akta
24
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
SOLUTION:
76 mm
Compute the product of inertia with respect to the xy axes
by dividing the section into three rectangles.
13 mm
Apply the parallel axis theorem to each rectangle,
102 mm
13 mm
76 mm
31.5 mm
44.5 mm
I xy I xy x yA
Note that the product of inertia with respect to centroidal
axes parallel to the xy axes is zero for each rectangle.
Rectangle Area, mm2 x , mm. y , mm.
I
988 31.5 44.5
II
988
0
0
III
988 31.5 44.5
44.5 mm
x yA, mm 4
1384929
0
1384929
xyA 2769858
I xy xyA 2770000mm4
31.5 mm
09.12.2014
Dr. Engin Akta
25
IZMIR INSTITUTE OF TECHNOLOGY
Department of Architecture
AR231 Fall12/13
tan 2 m
Determine the orientation of the principal axes by
m = 127.5o
the principal moments of
inertia by
2 I xy
Ix I y
I max, min I ave R
I x I ave 2 I x2y R 2
m =
I ave
37.5o
I m ax,m in
Ix Iy
2
Ix I y 2
I xy
R
2
2 m 74.9 and 254.9
m 37 .5 and m 127 .5
Ix Iy
I xy2
2
2
4.42 106 2.93 106
4.42 10 2.93 10
2.77 106
2
2
2 2.77 106
tan 2 m
3.72
6
6
Ix Iy
4.42 10 2.93 10
I y 2.93 106 mm4
I xy 2.77 10 mm
2 I xy
I x 4.42 106 mm4
6
Ix I y
I a I max 6.54 mm4
I b I min 8.07 mm4
09.12.2014
Dr. Engin Akta
26
Das könnte Ihnen auch gefallen
- Shoe Dog: A Memoir by the Creator of NikeVon EverandShoe Dog: A Memoir by the Creator of NikeBewertung: 4.5 von 5 Sternen4.5/5 (537)
- Grit: The Power of Passion and PerseveranceVon EverandGrit: The Power of Passion and PerseveranceBewertung: 4 von 5 Sternen4/5 (587)
- Swing Check Valve - Flanged: Technical FeaturesDokument1 SeiteSwing Check Valve - Flanged: Technical FeaturesAhmed El MorsyNoch keine Bewertungen
- PMF Activity GuideDokument7 SeitenPMF Activity GuideMarcia RodriguesNoch keine Bewertungen
- Viking pressure gauge technical dataDokument2 SeitenViking pressure gauge technical dataAhmed El MorsyNoch keine Bewertungen
- Test And Drain Valve SpecificationsDokument1 SeiteTest And Drain Valve SpecificationsAhmed El MorsyNoch keine Bewertungen
- Ancillary Equipment Page Features Electronic Bell SpecsDokument1 SeiteAncillary Equipment Page Features Electronic Bell SpecsAhmed El MorsyNoch keine Bewertungen
- RFP Conference Center Construction Project Management FundamentalsDokument1 SeiteRFP Conference Center Construction Project Management FundamentalsAhmed El MorsyNoch keine Bewertungen
- Change Request Log: Last Updated: 5-DecDokument3 SeitenChange Request Log: Last Updated: 5-DecAhmed El MorsyNoch keine Bewertungen
- SPP Fire Pumps - General Brochure PDFDokument8 SeitenSPP Fire Pumps - General Brochure PDFAhmed El Morsy100% (1)
- Choose The Correct Answer?: A-Cloven Hooved AnmalsDokument17 SeitenChoose The Correct Answer?: A-Cloven Hooved AnmalsAhmed El MorsyNoch keine Bewertungen
- Vendor Evaluation: Criteria For Evaluation CandidatesDokument2 SeitenVendor Evaluation: Criteria For Evaluation CandidatesAhmed El MorsyNoch keine Bewertungen
- 04 - 04 Work Package PDFDokument1 Seite04 - 04 Work Package PDFAhmed El MorsyNoch keine Bewertungen
- Monster CV Template Graduate - Mechanical - EngineeringDokument2 SeitenMonster CV Template Graduate - Mechanical - Engineeringvinh nguyenNoch keine Bewertungen
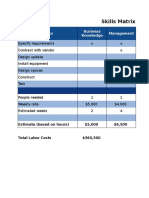
- 04 - 06 Skills MatrixDokument2 Seiten04 - 06 Skills MatrixAhmed El MorsyNoch keine Bewertungen
- Crash Table: Task Name Task Cost Task Duration Crash Reduction in WeeksDokument2 SeitenCrash Table: Task Name Task Cost Task Duration Crash Reduction in WeeksAhmed El MorsyNoch keine Bewertungen
- Task Name Progress Current Finish Variance: 4 Days Contract With VendorDokument2 SeitenTask Name Progress Current Finish Variance: 4 Days Contract With VendorAhmed El MorsyNoch keine Bewertungen
- Conference Center Project Schedule and Cost BaselineDokument2 SeitenConference Center Project Schedule and Cost BaselineAhmed El MorsyNoch keine Bewertungen
- Why Repetition?: Read 8 Real Numbers and Compute Their AverageDokument29 SeitenWhy Repetition?: Read 8 Real Numbers and Compute Their AverageAhmed El MorsyNoch keine Bewertungen
- PMPDokument3 SeitenPMPAhmed El MorsyNoch keine Bewertungen
- Ehaf-Load by Mohamed Nasr Version 2Dokument16 SeitenEhaf-Load by Mohamed Nasr Version 2Ahmed El MorsyNoch keine Bewertungen
- FORTRAN Lecture NotesDokument84 SeitenFORTRAN Lecture NotesAhmed El MorsyNoch keine Bewertungen
- Weekly Fire Pump TestingDokument6 SeitenWeekly Fire Pump TestingrahulNoch keine Bewertungen
- Mechanical Sales Fire Pump Test WorksheetDokument1 SeiteMechanical Sales Fire Pump Test WorksheetAhmed El MorsyNoch keine Bewertungen
- Company Origin Products: X MET 8000 SeriesDokument4 SeitenCompany Origin Products: X MET 8000 SeriesAhmed El MorsyNoch keine Bewertungen
- 19 - References PDFDokument3 Seiten19 - References PDFAhmed El MorsyNoch keine Bewertungen
- Alloying Elements PDFDokument2 SeitenAlloying Elements PDFAhmed El MorsyNoch keine Bewertungen
- 03 - Conservation Equations PDFDokument33 Seiten03 - Conservation Equations PDFAhmed El MorsyNoch keine Bewertungen
- Ehaf-Load by Mohamed Nasr Version 2Dokument3 SeitenEhaf-Load by Mohamed Nasr Version 2Ahmed El MorsyNoch keine Bewertungen
- Chemistry Vocab Record PDFDokument1 SeiteChemistry Vocab Record PDFAhmed El MorsyNoch keine Bewertungen
- لمصاعد لكهربائية دراسة رائعةDokument2 Seitenلمصاعد لكهربائية دراسة رائعةAhmed El MorsyNoch keine Bewertungen
- Vocabulary Record - Changes: Word Translation Picture Example SentenceDokument1 SeiteVocabulary Record - Changes: Word Translation Picture Example SentenceAhmed El MorsyNoch keine Bewertungen
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceVon EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceBewertung: 4 von 5 Sternen4/5 (894)
- The Yellow House: A Memoir (2019 National Book Award Winner)Von EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Bewertung: 4 von 5 Sternen4/5 (98)
- The Little Book of Hygge: Danish Secrets to Happy LivingVon EverandThe Little Book of Hygge: Danish Secrets to Happy LivingBewertung: 3.5 von 5 Sternen3.5/5 (399)
- On Fire: The (Burning) Case for a Green New DealVon EverandOn Fire: The (Burning) Case for a Green New DealBewertung: 4 von 5 Sternen4/5 (73)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeVon EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeBewertung: 4 von 5 Sternen4/5 (5794)
- Never Split the Difference: Negotiating As If Your Life Depended On ItVon EverandNever Split the Difference: Negotiating As If Your Life Depended On ItBewertung: 4.5 von 5 Sternen4.5/5 (838)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureVon EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureBewertung: 4.5 von 5 Sternen4.5/5 (474)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryVon EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryBewertung: 3.5 von 5 Sternen3.5/5 (231)
- The Emperor of All Maladies: A Biography of CancerVon EverandThe Emperor of All Maladies: A Biography of CancerBewertung: 4.5 von 5 Sternen4.5/5 (271)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreVon EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreBewertung: 4 von 5 Sternen4/5 (1090)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyVon EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyBewertung: 3.5 von 5 Sternen3.5/5 (2219)
- Team of Rivals: The Political Genius of Abraham LincolnVon EverandTeam of Rivals: The Political Genius of Abraham LincolnBewertung: 4.5 von 5 Sternen4.5/5 (234)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersVon EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersBewertung: 4.5 von 5 Sternen4.5/5 (344)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaVon EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaBewertung: 4.5 von 5 Sternen4.5/5 (265)
- The Unwinding: An Inner History of the New AmericaVon EverandThe Unwinding: An Inner History of the New AmericaBewertung: 4 von 5 Sternen4/5 (45)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Von EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Bewertung: 4.5 von 5 Sternen4.5/5 (119)
- Her Body and Other Parties: StoriesVon EverandHer Body and Other Parties: StoriesBewertung: 4 von 5 Sternen4/5 (821)
- Module 2Dokument59 SeitenModule 2PSkotsNoch keine Bewertungen
- Kinematics of Particle - N-T, R-Theta - ClassDokument33 SeitenKinematics of Particle - N-T, R-Theta - ClassLebogang TlhagwaneNoch keine Bewertungen
- Archimedes PrincipleDokument4 SeitenArchimedes Principleraviteja036Noch keine Bewertungen
- Sany Grader Parts ManualDokument436 SeitenSany Grader Parts ManualJohnson Lee93% (14)
- Parts Cataloque 2006Dokument47 SeitenParts Cataloque 2006keesNoch keine Bewertungen
- Landing GearDokument12 SeitenLanding GearcmpmarinhoNoch keine Bewertungen
- FVD SeminarDokument2 SeitenFVD Seminaranand_316764947Noch keine Bewertungen
- Section 8 Maintenance & SpecificationsDokument30 SeitenSection 8 Maintenance & SpecificationsTaha RdmanNoch keine Bewertungen
- 2022.08.08 Fabrication and Installation Steel StructureDokument21 Seiten2022.08.08 Fabrication and Installation Steel StructureArifian NugrohoNoch keine Bewertungen
- Solenoid Operated Deluge Valve: - UL Listed / ULC Listed Main Valves - 3 - 12 Inch SizesDokument2 SeitenSolenoid Operated Deluge Valve: - UL Listed / ULC Listed Main Valves - 3 - 12 Inch Sizeseng_poohNoch keine Bewertungen
- Strengthening Mechanisms ExplainedDokument74 SeitenStrengthening Mechanisms ExplainedRyan TorresNoch keine Bewertungen
- HP237Dokument20 SeitenHP237Asif HameedNoch keine Bewertungen
- Bending and Transverse TensionDokument23 SeitenBending and Transverse TensionAsghar Hussain ShahNoch keine Bewertungen
- Boiler Controls: Low Water Cut-Offs - Mechanical For Steam BoilersDokument1 SeiteBoiler Controls: Low Water Cut-Offs - Mechanical For Steam BoilersAlfredo Mitzi HernandezNoch keine Bewertungen
- 544-13 IndicatingDokument64 Seiten544-13 IndicatingHENIGUEDRINoch keine Bewertungen
- Fixed Free Fixed Free Plate PDFDokument7 SeitenFixed Free Fixed Free Plate PDFbeenaNoch keine Bewertungen
- Buckling Analysis: The Theory of BucklingDokument6 SeitenBuckling Analysis: The Theory of BucklingKing Everest100% (2)
- M.E. - Heat Power RGPV Syllabus 2011Dokument5 SeitenM.E. - Heat Power RGPV Syllabus 2011Arun MalviyaNoch keine Bewertungen
- Super Aero City CNG Bus: Owner'S Manual Operation Maintenance SpecificationsDokument208 SeitenSuper Aero City CNG Bus: Owner'S Manual Operation Maintenance SpecificationsHuu NguyenNoch keine Bewertungen
- Katalog Case Traktor 7230 Case Ih Magnum Diesel TractorDokument488 SeitenKatalog Case Traktor 7230 Case Ih Magnum Diesel TractorAlexey petrovich100% (2)
- Product CatalogDokument106 SeitenProduct CatalogAri AzadNoch keine Bewertungen
- Grindex Lista de PartesDokument28 SeitenGrindex Lista de PartesMarco Antonio Cerna HaroNoch keine Bewertungen
- Work Power Energy Faculty Copy Yw3bPNODokument92 SeitenWork Power Energy Faculty Copy Yw3bPNOSamridh GuptaNoch keine Bewertungen
- 2018 1 X Y HamadaDokument28 Seiten2018 1 X Y HamadaGaurav Kumar ThakurNoch keine Bewertungen
- Intelligent Air Duct Detectors: FeaturesDokument3 SeitenIntelligent Air Duct Detectors: FeaturesMarcelo FradeNoch keine Bewertungen
- Annual scissor lift inspection reportDokument1 SeiteAnnual scissor lift inspection reportWisnu WardhanaNoch keine Bewertungen
- MMA welding electrode changes and weld defectsDokument14 SeitenMMA welding electrode changes and weld defectsUmaibalanNoch keine Bewertungen
- 3784A KXX K4J K4M Clio Motor ManualDokument32 Seiten3784A KXX K4J K4M Clio Motor ManualDavid NebainNoch keine Bewertungen
- Atlas EbookDokument48 SeitenAtlas EbookVyas SrinivasanNoch keine Bewertungen
- Structural Design 1: Module inDokument4 SeitenStructural Design 1: Module inkangkongNoch keine Bewertungen