4.

3 Periodic Forcing Function

4.3.1 Fourier Series
A periodic forcing function is a forcing
function that repeats itself at equal intervals
of time T (The period of the function)
F

4.3 Periodic Forcing Function

4.3.1 Fourier Series

From mathematics it is known that a

FOURIER SERIES, which is a summation
of an infinite number of sine and cosine
terms, can be used to express a periodic
function.

4.3 Periodic Forcing Function

4.3.1 Fourier Series

For a periodic function, the FOURIER SERIES

may be written as:
F (t ) a0 a1 cos t a 2 cos 2t .... a n cos nt
[4.22]
b1 sin t b2 sin 2t ...... bn sin nt

or
an cos nt bn sin nt [4.23
F (t ) a 0
n 1
]
2 Is the frequency and T is the

where
T

period of the function

4.3 Periodic Forcing Function

4.3.1 Fourier Series
The evaluation of the coefficients a0, an and bn for
a given function F(t) is determined from the
t T
following expressions:
[4.24]
a0 1
T

an 2
T

F (t )dt
t1

t1 T

bn 2
T

F (t ) cos nt dt

[4.25]

t1

t1 T

t1

F (t ) sin nt dt

[4.26]
4

4.3 Periodic Forcing Function

4.3.1 Fourier Series

Where t1 in the limits of the integral

may be any value of time.

The constant a0 represents the

average of the periodic function

4.3 Periodic Forcing Function

4.3.2 Response to a Periodic Force
The response of a single degree of freedom
system to a
periodic force is determined as follows:
1. The periodic force is represented by its
FOURIER
series.
2. The response is then found as the
superposition of the response of each
component of the series.
Bellow the responses of UNDAMPED and DAMPED
6
single degree of freedom Systems to a periodic

4.3 Periodic Forcing Function

4.3.2.1 Response of UNDAMPED
Single
When the transient
response
Degree
of freedom System
i.e.

X c (t ) e

c t
2m

C1 cos D t C2 sin D t

Is omitted, the response of un damped single

degree of freedom system to any of the sine term
of the series is given by the particular integral
7
(Xp) (see Eq. 4.17) i.e.

4.3 Periodic Forcing Function

4.3.2.1 Response of UNDAMPED
Single
Degree of freedom System
X n( s ) (t )

Where
:

bn sin( n t )
k 1 rn2

[4.27]

rn n

[4.28]

k
m

See Eq. 2.5

4.3 Periodic Forcing Function

4.3.2.1 Response of UNDAMPED
Single
Similarly, the response to any cosine term is
Degree of freedom System
given by:
X n( C ) (t )

a n cos( n t )

[4.29]

k 1 rn

The total response may then be expressed as

the superposition of the responses to all the
ao
force terms

of the series, including the response

(steady state response to the constant force ao.

4.3 Periodic Forcing Function

4.3.2.1 Response of UNDAMPED
Single
Degree of freedom System
x(t ) a o
k

1
2
1 rn
n 1

a n cos nt bn sin nt
k
k

[4.30]

10

4.3 Periodic Forcing Function

4.3.2.1 Response of DAMPED Single
When the damping in the system is considered,
Degree of freedom System
the steady state response for the general sine
term of the series is given by Eq. 4.17 as follows
X n( S ) (t )

bn sin( n t )
k 1 rn2

With:

2 rn

[4.31]
2

2 rn
tan
2
1

r
n

11

4.3 Periodic Forcing Function

4.3.2.1 Response of DAMPED
Single
2
2
1 rn2 Degree
of
freedom

System

2 rn

2
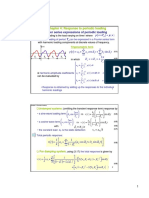
1 rn
Fig. 4.3: The Phase Angle

12

4.3 Periodic Forcing Function

4.3.2.1 Response of DAMPED
Single
From
Fig. 4.3 it follows:
Degree of freedom
2 rn
[4.32
sin
System
2
1 rn2

2 rn

cos

1 rn2

1 rn2

2 rn

[4.33
]
13

4.3 Periodic Forcing Function

4.3.2.1 Response of DAMPED
Single
From the relationship
Degree
freedom
[4.34]
sin( ) sin
cos of
cos
sin
System

It follows that Eq. 4.31 can be written in the

form :
bn (sin n t ) (cos ) (cos n t ) (sin ))
[4.35]
(S )
X (t )
n

k 1 rn2

2 rn

Substituting expressions for sin and cos

from Eqs. 4.32 and 4.33 into Eq. 4.35 gives

14

X n (t )

4.3 Periodic Forcing Function

4.3.2.1 Response of DAMPED
Single
(1 r ) (sin n t ) ( 2 r ) (cos n t )
b

Degree of freedom
1 r 2 r
k 1 r 2 r
System

2
n

2
n

2
n

Which can be simplified to:

2
(
1

r
) (sin n t ) ( 2 rn ) (cos n t ) [4.36
n
(S )
b
n
X n (t )

2
k
1 rn2 2 rn 2
]

15

4.3 Periodic Forcing Function

4.3.2.1 Response of DAMPED
Single
Similarly for a cosine term of the series one
Degree
of
freedom
gets:
2
System
(
1

r
) (cos n t ) ( 2 rn ) (sin n t )
[4.37
n
(C )
a
n
X (t )

1 rn2

2 rn

Recall:

cos( ) cos cos sin sin

[4.38
]
16

4.3 Periodic Forcing Function

4.3.2.1 Response of DAMPED
Single
Finally the total response is given by the
Degree
of freedom
superposition of the
terms expressed
by Eqs.
4.36 and
4.37
System

a ( 2 r ) b (1 r 2 )

X (t ) a o 1
k k

n 1

1 rn2

2 rn

(sin n t )

a n (1 rn2 ) bn ( 2 rn )

1 rn2

2 rn

(cos n t )

[4.39]

17

Recall:

4.3 Periodic Forcing Function

4.3.1t Fourier
Series
T
a0 1
T
an 2
T
bn 2
T

F (t )dt

See Eq.[4.24]

t1

t1 T

F (t ) cos nt dt

t1

See Eq.[4.25]

t1 T

t1

F (t ) sin nt dt

See Eq.[4.26]
18

4.3 Periodic Forcing Function

4.3.2.1 Response of UNDAMPED
Single
Degree of freedom System
rn n

k
m

See Eq.[4.28]

See Eq.[2.5]

c damping ratio
ccr
2 Frequecy of the Excitation
T
T Period of the Excitation

19

4.3 Periodic Forcing Function

4.3.2.1 Response of DAMPED
Single
Degree of freedom
System

20