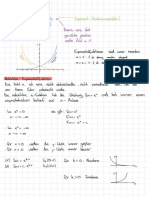
Spickzettel Lineare Algebra eigenwerte, Eigenvektoren, Eigenraum nonsingulär

1. Eigenwerte durch Lösen von det (A - λI) = 0 berechnen An×n ist nonsingular = invertierbar = regulär iff:
Es gibt eine Matrix B:= A-1, so dass AB = I = BA
Vektoren 2. Jeder Vektor x, der (A - λiI) x = 0 erfüllt, ist ein
det(A) 6= 0
Eigenvektor für λi.
punktprodukt: u ˙ v = ||u|| ˙ ||v|| ˙ cos(φ) = uxvx + uyvy
3. Eig (λi) = {x ∈ C : (A - λi)x = 0} Eigenraum für λi.
A
n
Ax = b hat genau eine Lösung für jedes b
(Uy Vz - Uz Vy \ uzvx - uxvz uxvy - uyvx Die Spaltenvektoren von A sind linear unabhängig
Normen: bestimmtheit rang(A) = n
p Pn
kxkp:= p
|xi|p
i =1 definiert auf n×n Quadratmatrizen: f (x) = Ax ist bijektiv (?)
kxk1:= i =1 |xi| kxk∞ =
Pn
max |xi| λ ∈ σ(A). ⇒ det(A)-1 = det(A-1)
i
eingeschlossener Winkel: λ > 0 ⇐⇒ positiv-definiert ⇒ (A-1)-1 = A
λ ≥ 0 ⇐⇒ positiv-semidefinit ⇒ (AT)-1 =(A-1)T
λ < 0 ⇐⇒ negativ-definit
diagonalisierbar
cos λ ≤ 0 ⇐⇒ negativ-semidefinit
u∗v ||u|| · ||v|| wenn nicht wahr (positives und negatives λ vorhanden): An×n kann diagonalisiert werden iff:
unbestimmt es hat n lineare unabhängige Eigenvektoren
||u|| ∗ ||v|| = (u
q 2
x + u )(v + v )
2
y x
2
y
2
äquivalent: z.B. x Ax > 0 ⇐⇒ positiv-definiert
T alle Eigenwerte sind real und eindeutig
es gibt ein umkehrbares T, so dass:
rang
Matrizen /X \
Sei A eine Matrix und f (x) = Ax. D:= T-1AT = I.. I
grundoperationen rang(A) = Rang(f) = Dim(im(f)) .
transpose: [A ]ij = [A]ji: ”mirror over main
T
= Anzahl der linear unabhängigen Spaltenvektoren von A λn
diagonal” conjungate transpose / adjugate: A ∗ = Anzahl der Zeilen ungleich Null in A nach dem
Anwenden von Gauß A = T -1DT und AT = TD
= (A) = A ”transpose and complex conjugate all
T T

entries” (same as transpose for real matrices) λ1, ... , λn sind die Eigenwerte von A!
kernel T kann mit Eigenvektoren von A erstellt werden und ist
multiplizieren: AN ×M ∼ BR×K = MN ×K
kern(A) = {x ∈ R : Ax = 0}
n
(die Menge der Vektoren, die nichtsingulär!
bl 1 = 1 [d -b d -b
1 . a auf 0 abgebildet werden)
invertie d = det(A) -c a -c a
diagonal dominante Matrix
ren:
ad-bc Für nicht singuläres A hat dies ein Element und
dim(kern(A)) = 0 (?) i.|aii| ≥ Pj6=i |aij|
c kAxkp
kAkp =
norm: m ax
x6= 0 kxk , induziert durch ⇒ nonsingulär
Vektor-p-Norm verfolgen
Hermitisch
kAk2 = pλmax (AT A)
span
definiert auf n×n Quadratmatrizen: tr(A) = a11 + a22 + ···+
Eine quadratische Matrix A mit A = A (gleich ihrem *
kAk1 = mjax Pim=1 |aij|, kAk∞ = m ax Pn
j =1 |
i
ann
Sei v1, ...der
, vr die Spaltenvektoren von A. Dann: Adjugat)
aij |, Bedingung: cond(A) = kAk · (Summe Elemente auf der Hauptdiagonale)
span(A) = {λ1 v1 + · · · + λr vr | λ1, ... , λr ∈ R} Eine reelle Matrix ist Hermitian iff symmetrisch
IIA-1|| ⇒ =(det(A)) = 0 (Determinante ist real)
spektrum dreieckig
determinanten σ(A) = {λ ∈ C: λ ist Eigenwert von A} Eine quadratische Matrix ist rechtwinklig dreieckig
det(A) = Pσ∈S sgn(σ) Qi =1 Ai,σ Fürn
n
(wlog n = 3):
3×3 Matrizen (Sarrus-Regel): eigenschaften a11 ai2 a13\
quadrat: N × N 0 a22 a23
0 0 a33
symmetrisch: A
= A T

⇒ Eigenwerte auf Hauptdiagonale

diagonal:
0 außer einem kk

⇒ impliziert dreieckig (Eigenwerte auf Hauptdiagonale) idempotent

Eine quadratische Matrix A, für die AA = A ist.
orthogonal
blockmatrizen
AT = A-1 ⇒ normal und diagonalisierbar
Sei B, C Teilmatrizen und A, D quadratische
einheitlich
Teilmatrizen. Dann:
Komplexe Analogie zu orthogonal: Eine komplexe <i.A0
rechenregeln: quadratische Matrix ist einheitlich, wenn alle .AB
det(A · B)= det(A) · det(B) Spaltenvektoren orthonormal sind det = det = det(A) det(D)
C D 0 D
det(A ) = det(A)
-1 -1

⇒ diagonolisierbar
det (rA) = r det A, für alle A n n×n
und
Skalare r ⇒ cond2 (A) = 1 minderjährige
⇒ |det(A)| = 1 Eine Matrix A hat Minors Mi j:= Zeile i und Spalte j aus
,

A entfernen Principle Minors: {det(obere linke i × i-

Matrix von A) : i..n} Sylvester-Kriterium für Hermitian A:
⇒ A ist positiv definiert, wenn alle Hauptminderjährigen
positiv sind